基于多项式混沌展开方法的翼伞飞行不确定性

刘安民，高峰，张青斌，袁天保，张国斌

(1.国防科技大学 空天科学学院，湖南 长沙 410073；2.96796部队，宁夏 银川 750000；3.96901部队，北京 100095)

0 引言

翼伞精确空投系统不仅具有普通降落伞弹道系数小、可折叠的优异特性，还具备更好的滑翔能力和可操控性，并且通过一定的制导控制，还能够实现精准着陆。因此，翼伞系统在部队突击、补给物资定点投送等领域都被广泛运用[1]，如加拿大MMIST公司研发的Snow Goose空投系统，美国Atair Aerospace公司研制的自主导航空投系统、美国Strong Enterprises公司研制的Screamer空投系统，以及加拿大米斯特机动综合系统技术公司研制的Sherpa系统等[2]。但是，飞行环境和系统参数等不确定性因素给翼伞空投系统的精确归航带来挑战，阻碍翼伞精确空投系统着陆精度的进一步提升，甚至会导致空投任务的失败[3]。在轨迹规划时进行不确定性优化可以增强翼伞系统归航策略的鲁棒性、提升归航性能[4]，而对飞行过程进行不确定性分析并研究翼伞系统对诸多不确定性因素的响应是整个优化过程的基础。因此，对翼伞系统飞行的不确定性分析具有重要意义。

工程应用中已经发展了大量系统不确定性分析的方法，其中基于大样本概率统计的Monte Carlo方法是应用最广泛的方法，其可靠性在工程实践中得到充分的验证，但是该方法的可靠性依赖于庞大的样本数量，当模型参数较为复杂时，存在计算量过大、效率低下的缺点。多项式混沌展开(PCE)是不确定性分析中较新的一种方法，该方法主要基于多项式混沌理论，具有坚实的数学基础和良好性能，在实践中也逐渐得到了广泛的运用。PCE方法最初在研究湍流问题中被Wiener[5]提出，这也被认为是PCE方法的起源，之后该方法也在计算流体力学领域被广泛运用。Wu等[6]利用非干涉式多项式混沌的方法对跨声速空气动力学的不确定性和灵敏度进行分析，研究了马赫数和翼型的不确定性对气动特性的影响，并且还利用稀疏网格法提高样本利用率，发现该方法比干涉式多项式混沌方法和Monte Carlo方法具有更高的效率。Prabhakar等[7]将PCE用于分析弹道系数、大气密度和升阻比等随机因素对高超声速飞行器轨迹的影响，证明了PCE方法可用于高超声速飞行中的不确定性研究，并且也得到该方法比Monte Carlo方法具有更高效率的结论。此外，PCE方法在翼型绕流[8]、火星着陆设计[9]和飞行器轨迹优化[10]等领域都得到运用，充分证明了其可靠性和计算效率。目前对翼伞空投系统的不确定性分析研究较少。

本文针对某小型载弹翼伞飞行中的气动参数不确定性问题，利用翼伞系统9自由度动力学模型，研究了PCE方法在翼伞系统飞行不确定性分析中的应用。考虑计算精度和效率，分析了多项式阶数和样本点数量对PCE模型计算结果的影响，得到适用于翼伞飞行不确定性分析的PCE模型。此外，通过与传统Monte Carlo法对比，验证了PCE模型的计算精度和可靠性。

1 翼伞系统多体动力学建模

1.1 模型描述

翼伞系统主要由伞衣、伞绳、吊带和荷载4部分组成。在稳定飞行阶段，伞衣充气后具有一定刚度而保持特定形状，并且伞绳和吊带材料强度大、变形小，故可以将伞衣和伞绳记为刚体P，质量为mP,将荷载和吊带记为刚体L,质量为mL.将地面记为零刚体，且零刚体质心坐标系与惯性系固连。刚体P具有质心平动和绕质心转动6个自由度,刚体L通过球铰Oc与刚体P连接,相对刚体P有3个转动自由度,建立如图1所示的翼伞系统9自由度多体动力学模型。

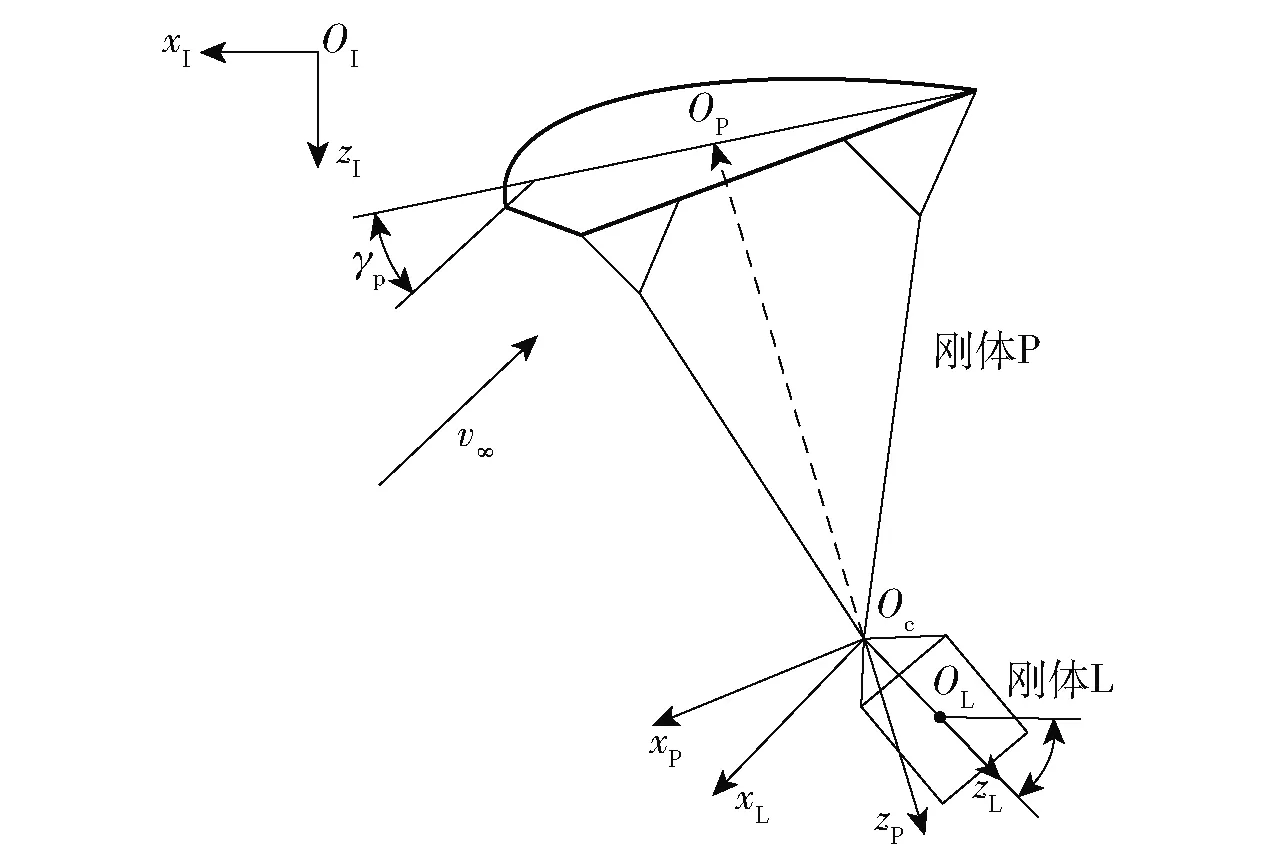
图1 翼伞系统9自由度模型

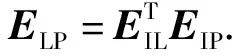
1.2 受力分析

假设伞衣气动压心与其几何中心重合，位于弦向距离前缘1/4处[11]，则伞衣气动力FP和气动力矩MP计算分别为

(1)

(2)

式中：ρ为气体密度；va是翼伞相对大气的运动速度；SP为翼伞的参考面积；CD、CL和CY分别为伞衣受到的气动阻力、升力和侧力系数，Cl、Cm和Cn为伞衣受到的滚转、俯仰和偏航气动力矩系数，用多项式形式[12]表示为

(3)

(4)

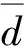
荷载为带螺旋桨的刚体，为简化计算，不考虑其气动力矩和螺旋桨对荷载气动力的影响，荷载所受气动力记为FL，其值为

(5)

式中：vL为荷载质心速度；SL为荷载阻力面积；CDL为荷载阻力系数。

除气动力，荷载还受螺旋桨推力Ft，两刚体重力GP和GL分别作用于各自质心位置。

1.3 动力学方程

伞衣充气后平均密度与空气密度相近，所以必须考虑附加质量效应。本文采用Barrows计算附加质量的方法[13]：在平直翼附加质量计算方式的基础上，考虑翼伞沿展向圆弧型的弯曲影响，计算得到翼伞的平动附加质量矩阵与绕各主惯性轴的转动附加质量矩阵，并将附加质量平动分量和转动分量写成矩阵形式Ma和Ja.在伞体坐标系下，相对于坐标原点Oc的附加质量惯量张量矩阵为Ja,Oc.

引入9自由度模型下的系统广义质量矩阵Am及广义力矩阵Bf：

Am=

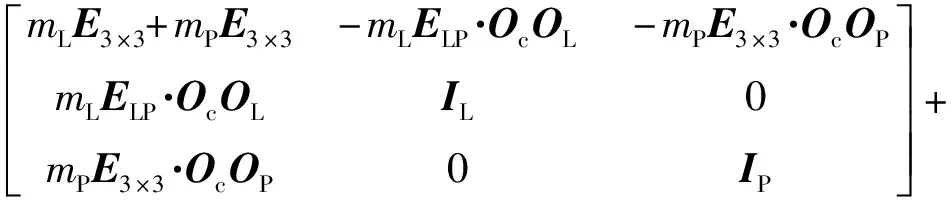
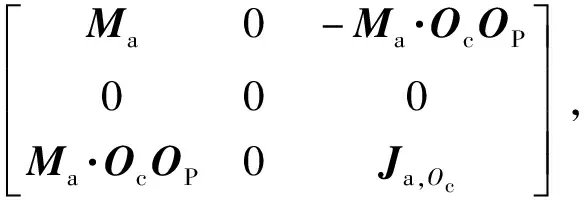
(6)

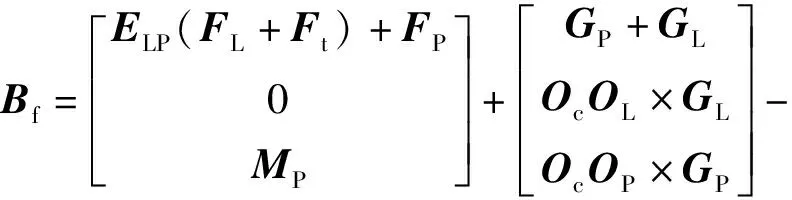
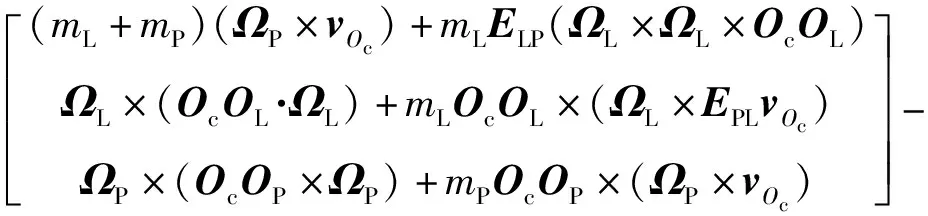
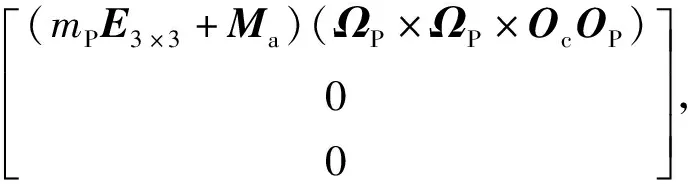
(7)

式中：ΩP和ΩL分别为刚体P和刚体L的角速度；IP和IL分别为两刚体相对质心的惯量张量；vOc为铰点速度；E3×3为3阶单位矩阵。

将伞体坐标系原点建立在铰点Oc处，避免了翼伞和荷载两体之间相对约束力的出现。在惯性坐标系下，以铰点Oc的位置坐标XOc=[xOc,yOc,zOc]T、刚体P姿态角ψP=[φP,θP,ζP]T和刚体L的姿态角ψL=[φL,θL,ζL]T为广义坐标，φ、θ、ζ分别为对应刚体的滚转角、俯仰角和偏航角。根据Newton-Euler方程，建立翼伞系统的动力学方程为

(8)

由于翼伞和荷载两体是通过铰点Oc联结，补充Oc点在飞行过程中位移的运动学关系:

(9)

式中：P=[xP,yP,zP]T为Oc点在伞体坐标系下的位置坐标。

建立的9自由度翼伞系统多体动力学模型已得到研究验证，证明了该模型的有效性[11-12]。但是，风洞试验或计算流体力学方法得到的气动参数与真实飞行数据存在一定误差，翼伞系统动力学模型中的气动力系数存在不确定性[14]。因此，本文将翼伞系统的气动参数偏差作为随机输入，假设真实气动力系数和气动力矩系数均为服从均匀分布的独立随机变量，标准差都为0.10[3].

2 PCE方法

本文采用非干涉式的PCE方法，该方法可以分为建立PCE模型、求解PCE系数和概率特性分析。

2.1 模型描述

PCE的原理是将受各分量相互独立的多维随机变量ξ=[ξ1ξ2…ξn]影响的系统输出表示为所有随机变量的多项式加权线性组合的形式[15]，将随机变量的个数n称为PCE的维数，对于随机响应Y(ξ)可以展开为

(10)

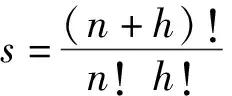
(11)

根据随机变量分布类型，从Wiener-Askey系列超几何正交多项式中选取相应多项式作为基函数，从而确保所得PCE方法的收敛速度，如均匀分布基函数为Legendre多项式、正态分布采用Hermite多项式作为基函数等。

2.2 PCE系数的确定

由2.1节确定的PCE模型中，基函数根据随机变量的分布对应选取，正交多项式由基函数组合得到，方程中更重要的是确定PCE系数。目前已经发展多种求解PCE系数的方法，Galerkin投影法和回归法是最常用的两种。回归法利用样本真实响应与PCE模型预测值的相对误差最小为条件求解系数[16]，本文采用回归方法求解PCE系数。

在标准随机空间中选取N个样本点{ξ1,ξ2,…,ξN}，并将标准随机空间的样本变换到原随机空间得到样本点{X1,X2,…,XN}，在原随机空间的样本点上调用真实响应函数，得到各样本点的真实响应值G[17]，则PCE方程在样本点上可以表示为

Ab=G，

(12)

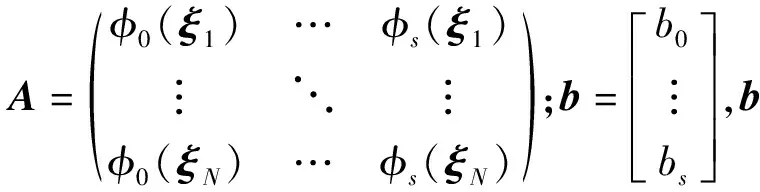
通常样本点数目远大于待求系数个数[18]，则(12)式为超定方程，可以通过线性最小二次回归方法解得系数矩阵。对于高维随机空间，需要的样本数量也随之增加，为避免“维数灾难”则需要通过特殊的采样方法抽取样本点进行回归分析，例如拉丁超立方抽样、加权的高斯积分点抽样以及单项求容积法则抽样等。本文采用各维均匀分布的拉丁超立方抽样方法，将各维随机变量均匀划分为N个等概率区间，并在各区间内随机生成1个1维样本点，最后将各维度的样本点随机组合得到随机空间中的样本向量。该方法在降低所需样本点数量的同时保证了其均匀性。

根据线性最小二次回归求PCE系数：

(13)

式中：g(Xj)为真实响应函数值；(ξj)为基于PCE模型的各样本点的随机响应函数值，则最小二次回归得到系数为

b=(ATA)-1ATG.

(14)

求得PCE系数后就可以构建完整的PCE模型，相当于构建了真实响应的代理模型，输出量的概率特性(统计矩、概率密度函数等)可以通过在随机空间调用代理模型求得。

3 翼伞飞行不确定性分析

3.1 问题描述

翼伞模型基于某小型载弹翼伞，如图2所示，翼伞系统基本参数如表1所示。翼伞系统初始高度为1 000 m，相对气流具有7.5 m/s的初始水平速度，下落初始速度3.8 m/s，无初始角速度。刚体L相对刚体P初始时刻无相对速度和角速度，初始偏航角为30°，其余姿态角为0°.翼伞系统飞行总时间为400 s，在滑翔20 s后施加转弯控制。

图2 某小型载弹翼伞

表1 翼伞基本参数

3.2 模型阶数与样本数量分析

由2.2节可知，建立考虑6个气动力系数随机性的6维h阶PCE模型，一共有s=(6+h)!/(6!h!)项待求PCE系数，而求解精度依赖于样本点的选取。模型阶数和样本点数量直接影响计算精度，因此针对以上因素展开分析。

为对比各阶PCE模型的精度，设置足够大的样本点数量(500个样本点)，分别计算各阶模型结果的均值和标准差，并统计h阶模型计算结果相对h-1阶模型的变化值(h=3,4,5)。图3给出了各阶模型相对变化值的结果，可以看出均值和标准差的相对变化值随着阶数升高而逐渐收敛。4阶PCE模型相对于3阶PCE模型的结果相对变化值达到收敛：位移均值相对变化值在0.042 m以内，标准差的相对变化值也小于0.74 m；速度均值相对变化值低于0.003 6 m/s，标准差相对变化值在0.055 m/s量级；偏航角的动力学方程非线性度较低，低阶模型的相对变化值就达到10-4量级。

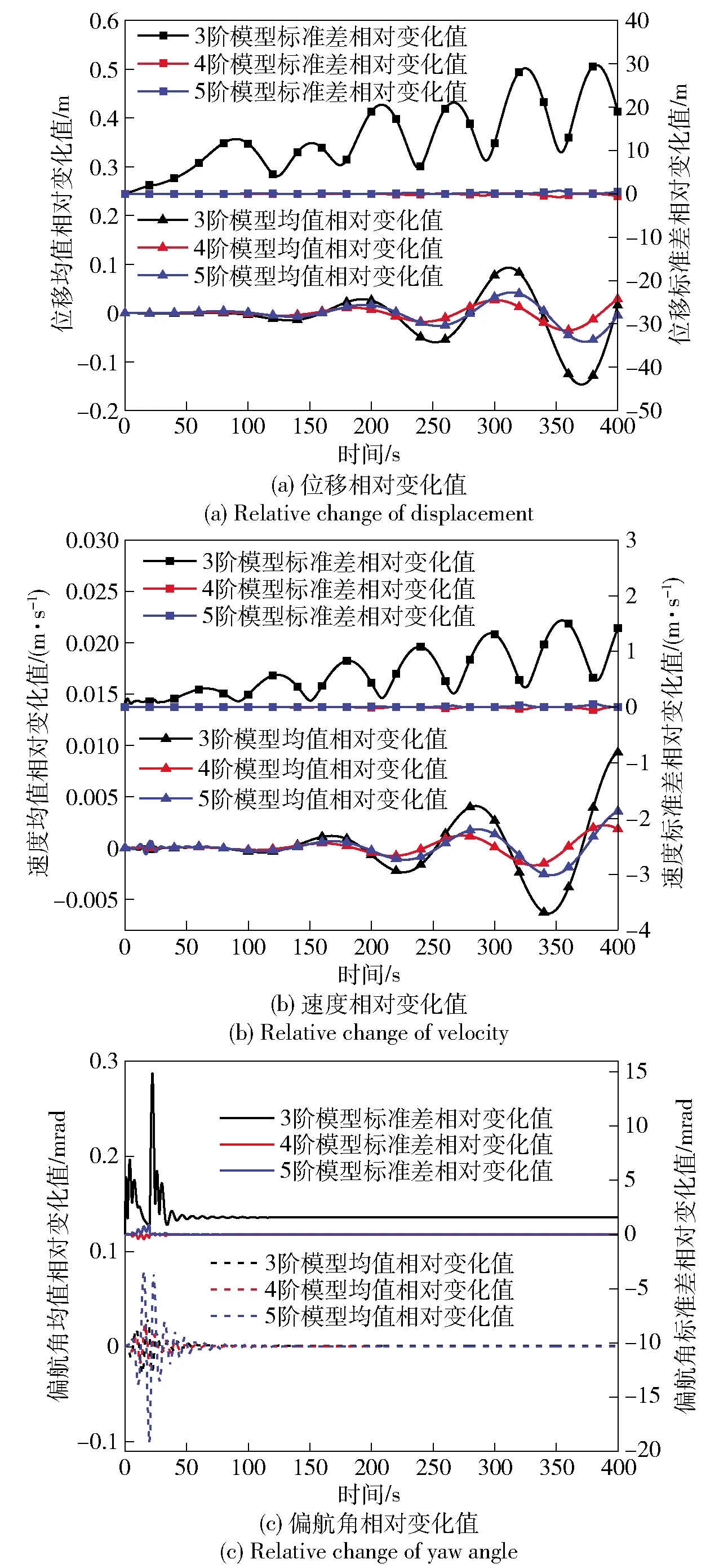
图3 不同多项式阶数的相对变化值比较

实际运用中，在达到收敛后提高模型阶数所带来的精度提升有限，但是计算量增大，因此需要综合计算精度和效率来选择合适的模型阶数。对于本文翼伞系统的不确定性分析可以选择3阶PCE模型。

为研究样本点数量对PCE模型精度的影响，设置3阶PCE模型的样本点数量N分别为s的整数倍(N=s,2s,3s,4s,5s)，并分别计算翼伞系统飞行过程中结果均值与标准差的相对变化值。计算结果表明，如果达到精度要求，则样本点数量至少为2s，2s个样本点相对于s个样本点的位移、速度均值相对变化值分别高达3.82 m和0.21 m/s，标准差相对变化量分别为0.69 m和0.056 m/s.样本点数量大于2s的相对变化值如图4所示，从图中可以看出过程中样本点数量在3s时，相对变化值就达到收敛，继续增加样本点数量对于精度提升作用不明显。

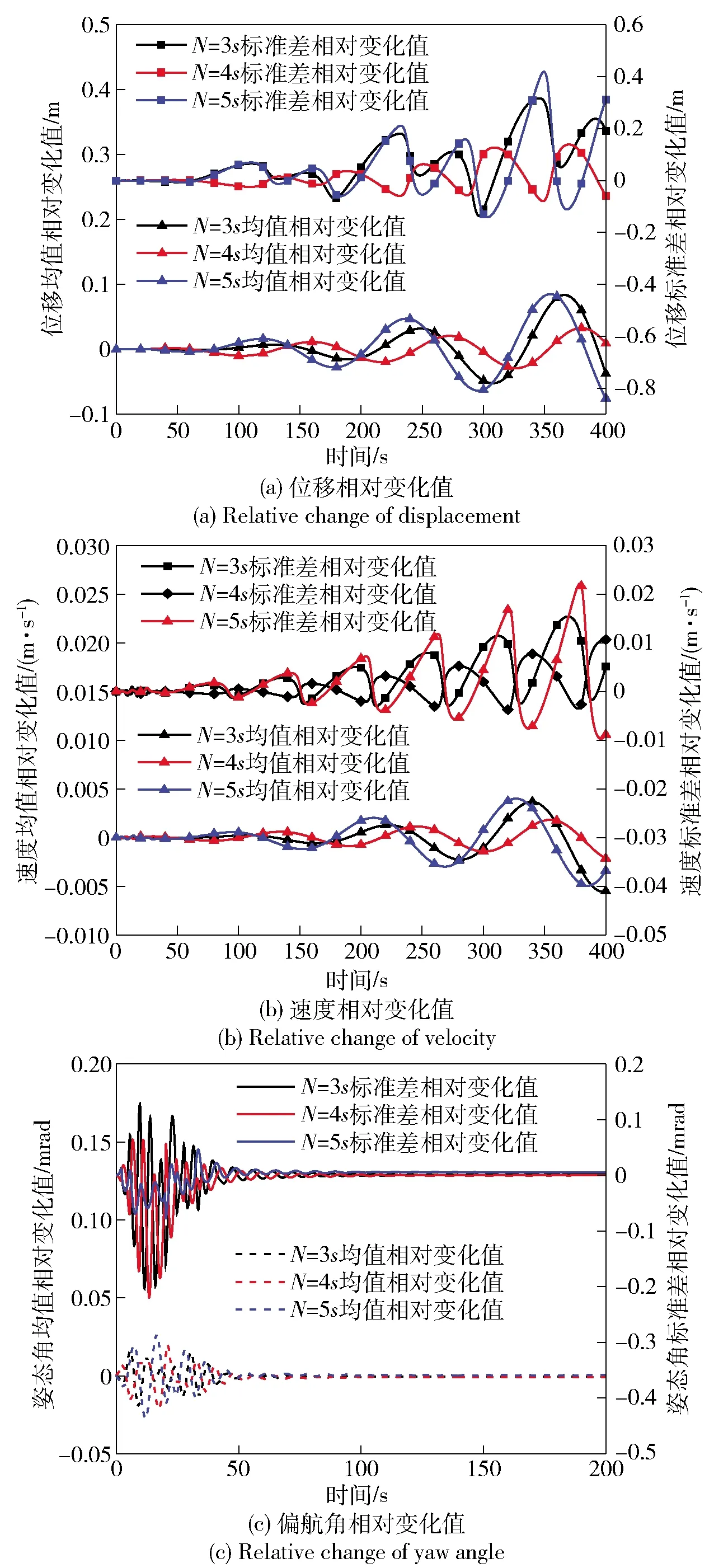
图4 不同样本点结果的相对变化值

通过以上分析，对于翼伞飞行的不确定性研究选择3阶PCE模型、样本点数量为3s可以满足计算精度。

3.3 与Monte Carlo方法对比

基于3.2节对PCE模型阶数和样本点数量的分析，PCE方法可选择多项式截断于第3阶，均匀选取252个样本点。Monte Carlo方法则直接在三维随机空间中生成5 000个样本点。分别采用PCE方法和Monte Carlo方法计算翼伞系统飞行过程中位移的均值和标准差，并将Monte Carlo方法计算结果作为参考值，计算PCE方法的相对偏差。

如图5所示，比较两种方法飞行过程中位移、速度以及偏航角的均值和标准差，结果表明两种方法的结果一致。图6给出了PCE方法计算结果相对Monte Carlo方法的偏差。偏航角的均值相对偏差在一段时间后达到稳定且保持在在10-4量级，标准差稳定时也低于2.5%；速度均值和标准差变化有周期性规律，其相对偏差也呈周期变化，其均值相对偏差不超过1.5%，标准差相对偏差也小于4.2%；位移的均值相对误差在0.025%以内且标准差相对偏差也小于5.6%.通过与Monte Carlo方法的对比，证明了PCE方法在翼伞飞行过程中不确定性分析的适用性。

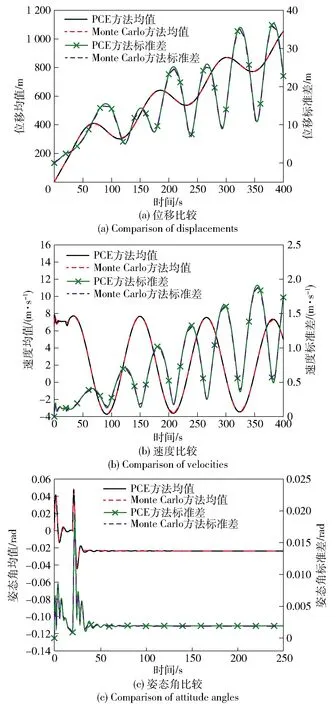
图5 PCE方法与Monte Carlo方法的均值和标准差比较

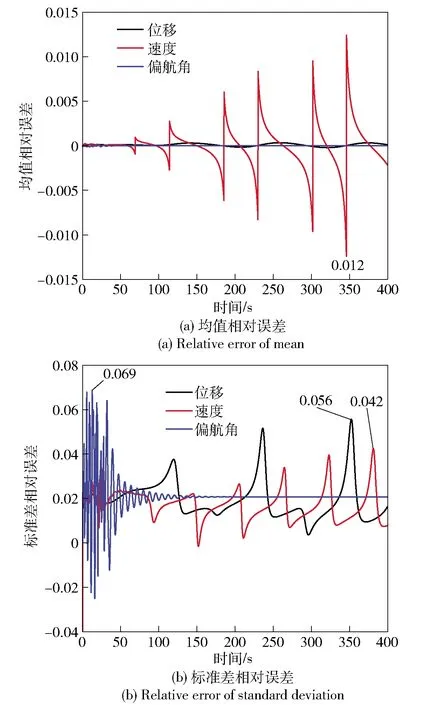
图6 PCE方法与Monte Carlo方法的相对误差比较

更重要的是，Monte Carlo方法计算了5 000个样本点，耗时近12.5 h，而PCE方法仅利用252个样本点，耗时仅0.5 h，二者达到几乎相同的精度。说明PCE方法在相同精度下的效率远高于Monte Carlo方法，在翼伞飞行或归航的不确定性分析和灵敏度分析中，该种方法具有更大的价值。

通过PCE方法建立了翼伞飞行过程不确定性传播的代理模型，该模型基于简单多项式的线性组合，避免了对原响应复杂动力学过程的计算，显著提高了计算效率。利用已经建立的PCE模型可以快速计算翼伞飞行过程中的状态变量分布。分别利用Monte Carlo方法和PCE方法预测受气动力系数不确定性影响的翼伞系统落点，Monte Carlo方法历时3 h，PCE方法基于已有模型仅耗时0.44 s.图7为两种方法计算落点分布密度图，PCE方法得到的落点分布与Monte Carlo方法结果一致，落点大部分集中在确定条件下的着陆位置附近，偏离距离越远分布点越少，Monte Carlo方法结果的最大误差距离为125.33 m，PCE方法最大误差距离为126.83 m.

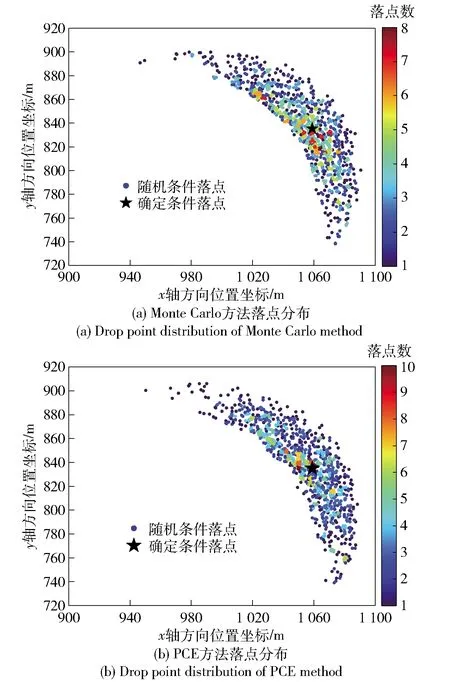
图7 两种方法的落点分布

4 结论

本文针对翼伞飞行的不确定性问题，利用翼伞系统9自由度动力学模型，建立了考虑气动参数不确定性的PCE模型，并分析了PCE模型的阶数和样本点数量对计算精度的影响。得出以下主要结论：

1)多项式截止于3阶、样本点数量为3s时，既能满足计算精度要求又具有较高计算效率。

2)利用Monte Carlo方法对PCE方法结果进行对比验证，结果显示均值相对误差不超过1.5%，标准差相对误差也在5.6%以内，两种方法可以达到相同的精度。但是，PCE方法仅调用252次原响应函数就可以得到Monte Carlo方法计算5 000次的结果，前者具有更高的效率。分别用Monte Carlo方法和PCE方法计算翼伞系统落点分布，两方法结果一致，最大误差可以达到120 m以上。PCE方法可以为翼伞精确空投任务的性能评估与优化提供一种新思路和理论参考。