越野环境下基于势能场模型的智能车概率图路径规划方法
2021-08-27田洪清王建强黄荷叶丁峰
田洪清,王建强,黄荷叶,丁峰
(清华大学 汽车安全与节能国家重点实验室,北京 100084)
0 引言
智能车能够在复杂越野环境中完成情报获取、侦察监视和通信中转等任务,具有不可替代的作用[1]。越野环境下的智能车路径规划是指在有界空间内根据感知系统输入的越野环境信息,考虑到环境和车辆等多种约束条件基础上,生成从初始位置到达指定目标安全可行的行驶优化路径[2]。路径规划对智能车在越野环境中完成驾驶行为起到至关重要的作用[3]。
近年来智能车路径规划技术发展迅速,建立了完整的理论体系[4]。基于图搜索的路径规划方法采用扩展启发搜索技术,其经典规划算法包括Dijkstra算法、A*算法、D*算法、Field D*算法及其多个变种等[5],其中Hybrid A*算法成功应用于非结构化道路环境下智能车路径规划系统[6]。随机采样路径规划算法,如随机快速搜索树(RRT)算法[7]、概率图(PRM)算法[8],以及渐进优化随机快速搜索树(RRT*)算法、信息优化随机快速搜索树(Informed RRT)算法、渐进优化概率图(PRM*)算法通过在一定范围[9],或一定时间内持续采样的方法优化路径[10],并使用环境信息启发来提升路径规划的效率或优化程度[11-12]。人工势能场(APF)算法将环境信息抽象为引力或斥力场,通过势能场的引导来规划从起始点到目标点的无碰撞路径[13]。几何曲线法将智能车路径规划问题转化成两点边界值问题求解,如B样条曲线[14]、5次多项式曲线[15]等。
在越野环境路径规划方面,文献[16]通过采集地形信息进行随机采样路径规划。文献[17]通过建立优化搜索方向和速度的规划模型,采用自适应变异遗传算法,在连续时空内进行多目标最优路径规划。文献[18]提出了改进型A*路径优化算法,通过分析地形坡度和地表属性的综合影响,采用窗口移动法来提高搜索效率。
本文将PRM算法与APF算法结合,通过环境态势建模、通行代价评估和路径平滑的方法对传统PRM算法进行改进,以满足复杂越野环境下,不同类型车辆安全行驶、高效通行和运动学约束的综合要求。综合APF算法和PRM算法,形成一种越野环境下智能车路径规划方法,称为APF-PRM算法,其框架结构如图1所示。该算法首先建立多层次环境态势场模型;然后采用随机采样方法,生成节点间的连通矩阵和多维度通行代价评估矩阵;通过评估矩阵衡量路径的可行性和安全性,并根据环境和车辆的约束条件,规划适应车辆特性的优化路径。图1中,vo为起点,vg为终点,T1为环境威胁,P1、P2为越野道路,Z1~Z4为禁行区。
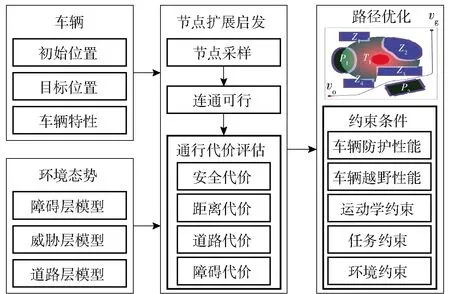
图1 APF-PRM算法路径规划框架结构
APF-PRM算法路径规划结合了PRM算法与APF算法的优点,适用于复杂越野环境。在路径规划过程中综合考虑了障碍物、环境威胁、道路条件等多种约束条件,以及车辆防护性能、越野性能、运动学特性,能够生成安全可行的车辆运动路径。
1 越野环境建模
本文采用APF算法对车辆所在越野环境进行栅格化环境态势场建模。环境态势场即一定环境空间范围内,根据越野环境中各栅格点的势能分布,建立多层次势能场模型,融合为环境态势场模型,如图2(a)所示。
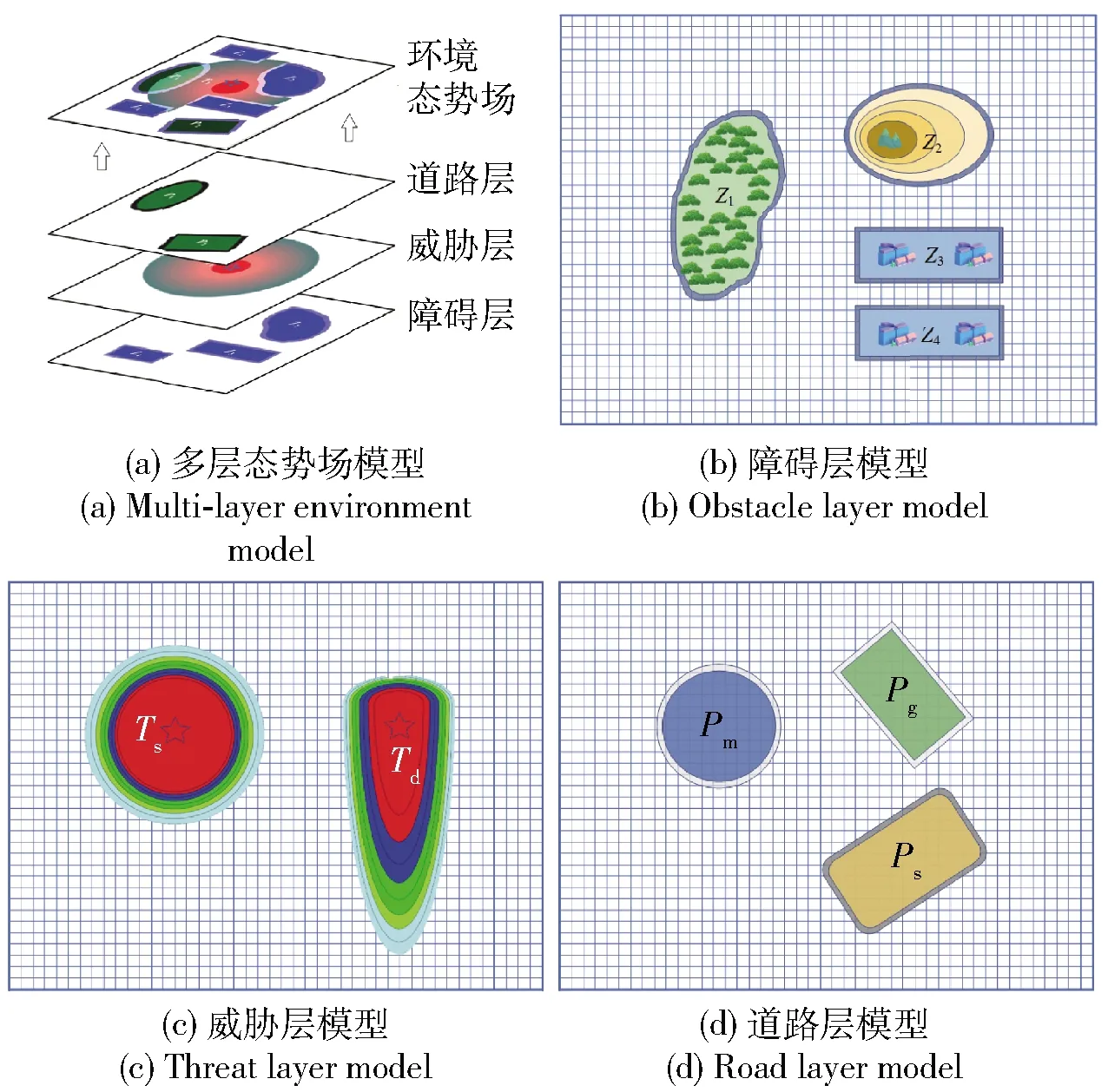
图2 多层次越野环境态势场模型
1.1 障碍层模型
障碍层模型即将存在建筑、树林、山地等不可穿越障碍物的越野环境划分为禁行区和可行区,并考虑到车辆的宽度和转弯半径等因素,在障碍物周边设置限制区。如图2(b)所示越野环境中有障碍层禁行区Z1~Z4,其周边为障碍层限制区,障碍层限制区外为安全通行区,障碍层模型为
(1)
式中:UB为障碍层势能场;Ub为障碍层禁行区势能场;Ur为障碍层限制区势能场;Z为禁行区域,Zi∈Z;z为限制区宽度;Uf为障碍层禁行区和限制区之外的安全通行区势能场;(xi,yi)为越野环境栅格点坐标。
1.2 威胁层模型
威胁层模型是将环境威胁对车辆行驶造成毁伤损失风险程度进行量化处理。环境威胁所产生的风险程度取决于威胁的属性、数量和状态等因素,本文基于APF算法[19]用威胁层模型来表征环境威胁对车辆造成的风险程度,威胁层模型为
(2)
(3)
式中:UT为威胁层势能场;r为环境威胁T与行驶车辆之间的距离;rmin为环境威胁所产生的有效作用距离,在[0,rmin]区间范围内为威胁有效区,其势能场为Ue;rmax为环境威胁所能产生的最远威胁作用距离,在[rmin,rmax]区间范围为威胁影响区,其势能场为Ua,Ua值随r的增大而减小;kw为环境威胁的威胁系数,由环境威胁的种类、数量和状态等因素决定;在[rmax,∞]区间范围为安全通行区,其势能场为Uf.
如图2(c)所示,越野环境中存在静态环境威胁Ts和动态环境威胁Td,通过威胁层模型可将环境空间划分为威胁有效区、威胁影响区和安全通行区3部分。
1.3 道路层模型
道路层模型是将越野环境中结构化道路、土路、草地、沙地、沼泽、山地等不同的地表属性特征对车辆通行影响进行量化处理,设通行条件最好的结构化道路势能场为Us,而通行条件最差的泥沼道路势能场为Uh,越野道路区周边为越野道路扩展区,道路层模型可用式描述:
(4)
式中:UR为道路层势能场;kr为越野道路区通行系数;P为越野道路区;p为越野道路扩展区宽度;ke为越野道路扩展区通行系数。参照轮式车辆和履带式车辆的实验数据和专家经验值,将道路通行系数按地表属性设置等级[20],如表1所示。
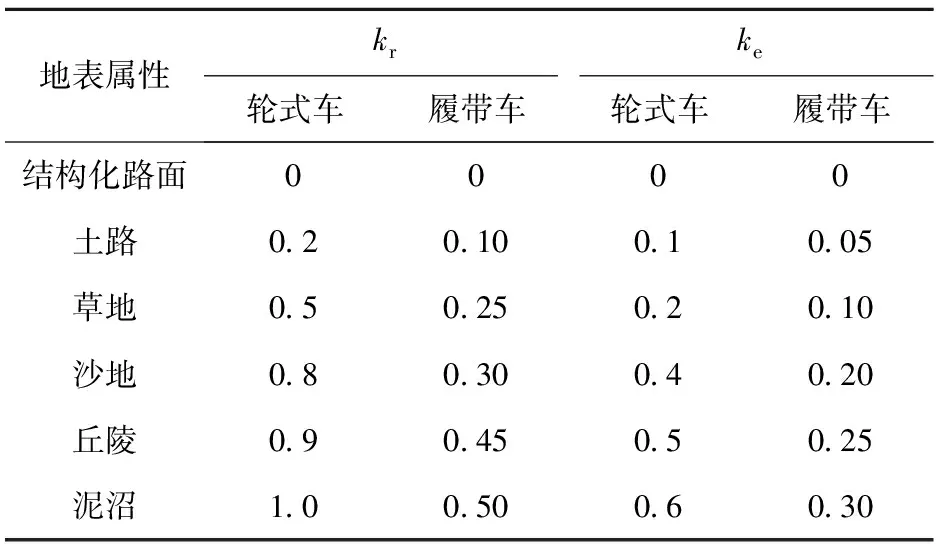
表1 地表属性与道路通行系数
如图2(d)所示越野环境中有3片越野道路区,通过道路层模型可将其划分为黄色沙地区Ps,绿色草地区Pg,蓝色泥沼区Pm,考虑车辆的宽度和弯道行驶情况,越野道路区周边一定范围设定为越野道路扩展区。各区域的道路层势能场可由(4)式计算。
1.4 环境态势场融合
路径规划时对各层势能场模型进行跨层融合,并考虑障碍物对环境威胁的遮挡,障碍层、威胁层与道路层的叠加等耦合作用,形成环境态势场,如(5)式、(6)式所示:
U=∑UB+∑UT+∑UR,
(5)
(6)
2 车辆路径规划
为权衡复杂越野环境下车辆行驶安全性与行车效率的关系,规划安全可行的行车优化路径,本文提出APF-PRM算法。算法分为离线采样学习和在线路径优化2个阶段。
2.1 离线采样学习
2.1.1 越野环境采样
首先将越野环境划分成为均匀分布的栅格化平面空间W,并建立车辆、起始点、目标终点、障碍物、环境威胁和越野道路等所在的位置特征。然后在可行的越野环境内生成采样节点,并形成越野环境拓扑图G=(V,E),V为采样节点v集合,E为采样节点之间的路段e集合。
采样节点v生成于平面空间W内,并选取在障碍层禁行区Z和威胁层环境威胁T的威胁有效区之外,如(7)式所示:
V={v|v∈W,v∉B∪T,vi≠vj}.
(7)
2.1.2 节点连接评估模型
节点连接评估即评估各采样节点之间连接路段的可行性和通行代价,可行性评估用连通矩阵描述,通行代价评估用多维度通行代价评估矩阵描述,并分为扩展代价评估和启发代价评估,如图3所示。
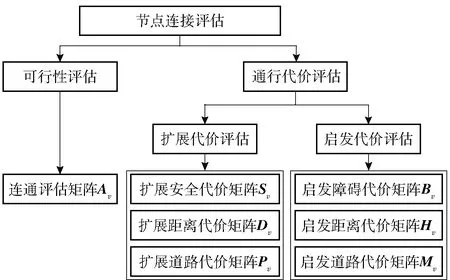
图3 节点连接评估模型
2.1.2.1 连通矩阵
为判定节点间的可行性,利用采样节点间连通性建立矩阵Av,用节点之间的连通属性作为连通矩阵Av的元素aij.采样节点与连通矩阵对应关系如图4所示,图4(a)中越野环境包含障碍区Z1和采样节点v1~v3,其连通矩阵Av如图4(b)所示。
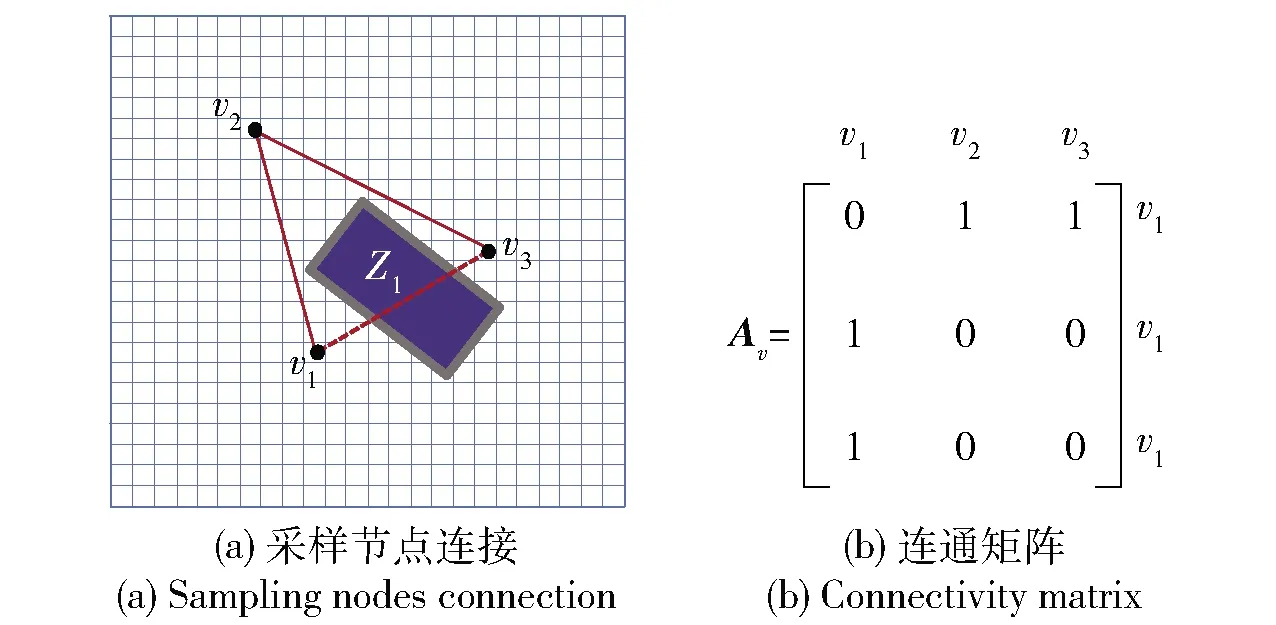
图4 越野环境采样节点连接与对应的连通矩阵
2.1.2.2 通行代价评估矩阵
通行代价评估矩阵由扩展代价评估矩阵和启发代价评估矩阵组成。扩展代价评估矩阵包括扩展安全代价矩阵Sv、扩展距离代价矩阵Dv和扩展道路代价矩阵Pv;启发代价评估矩阵包括启发障碍代价矩阵Bv、启发距离代价矩阵Hv和启发道路代价矩阵Mv.
扩展安全代价矩阵Sv由采样节点集合V中节点间的安全代价sij构成。评估方法是在采样节点之间的路段上取数量为n的均匀分布采样子节点vs(1)~vs(n),用各子节点所在的威胁层势能场累加和评估路段安全性,如(8)式所示。
(8)
多个节点之间路段的通行安全评估用扩展安全代价矩阵表示,如图5(a)、图5(b)分别表征包含环境威胁T1的越野环境及其对应的扩展安全代价矩阵。
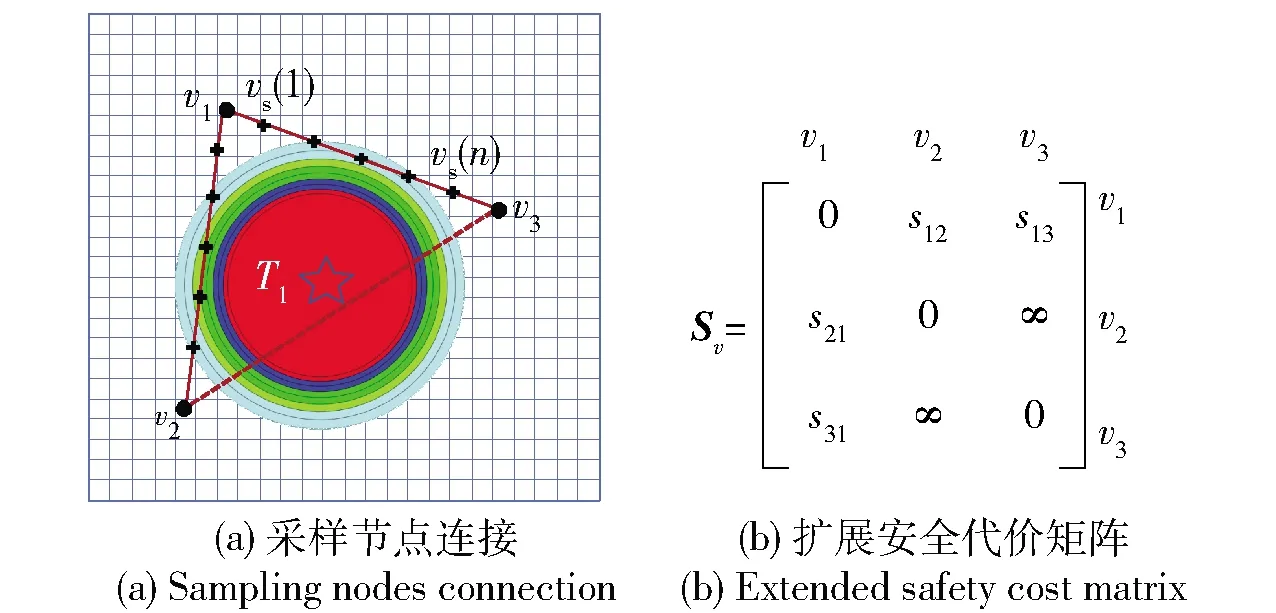
图5 越野环境采样节点连接与扩展安全代价矩阵
扩展距离代价矩阵Dv由集合V中节点间欧式距离dij构成,其计算方法为
(9)
多个节点之间路段的通行距离评估用扩展距离代价矩阵表示,如图6(a)、图6(b)分别表征包含障碍物Z1的越野环境及其对应的扩展距离代价矩阵。
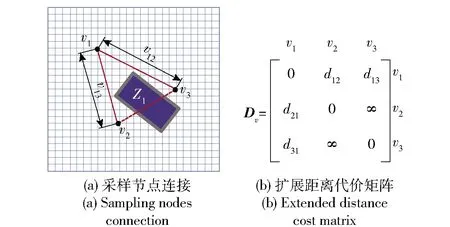
图6 越野环境采样节点连接与扩展距离代价矩阵
扩展道路代价矩阵Pv由集合V中节点间的道路代价pij构成,通过在节点之间的路段采样,用各采样子节点vr(1)~vr(n)所在道路层势能场累加和来评估该路径的道路通过性,如(10)式所示:
(10)
多个节点之间路段的通行道路评估用扩展道路代价矩阵表示,如图7(a)、图7(b)分别表征包含越野道路P1~P2的越野环境及其对应的扩展道路代价矩阵。
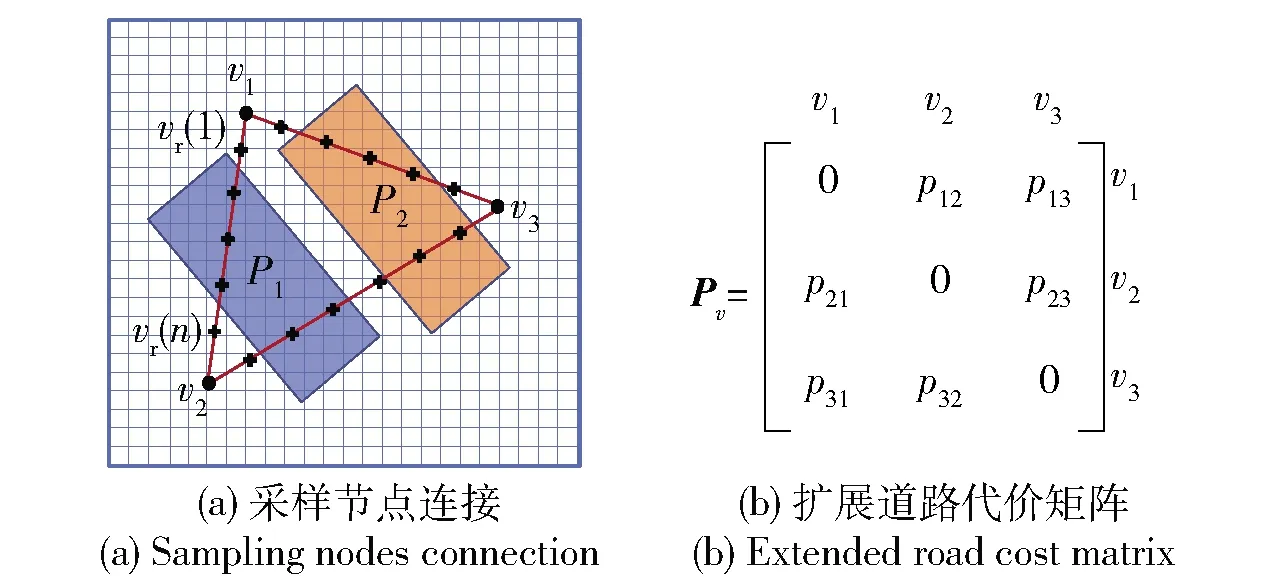
图7 越野环境采样节点连接与扩展道路代价矩阵
启发障碍代价矩阵Bv由集合V中节点vi与目标终点vg之间的启发障碍代价big构成。通过在采样节点与终点间的路段中各子节点vb(1)~vb(n)所在的障碍层和威胁层势能场累加和来评估,如(11)式所示:
(11)
节点vi与目标终点vg之间路段的通行障碍评估用启发障碍代价矩阵表示,如图8(a)、图8(b)分别表征包含障碍物Z1、环境威胁T1的越野环境及其对应的启发障碍代价矩阵。
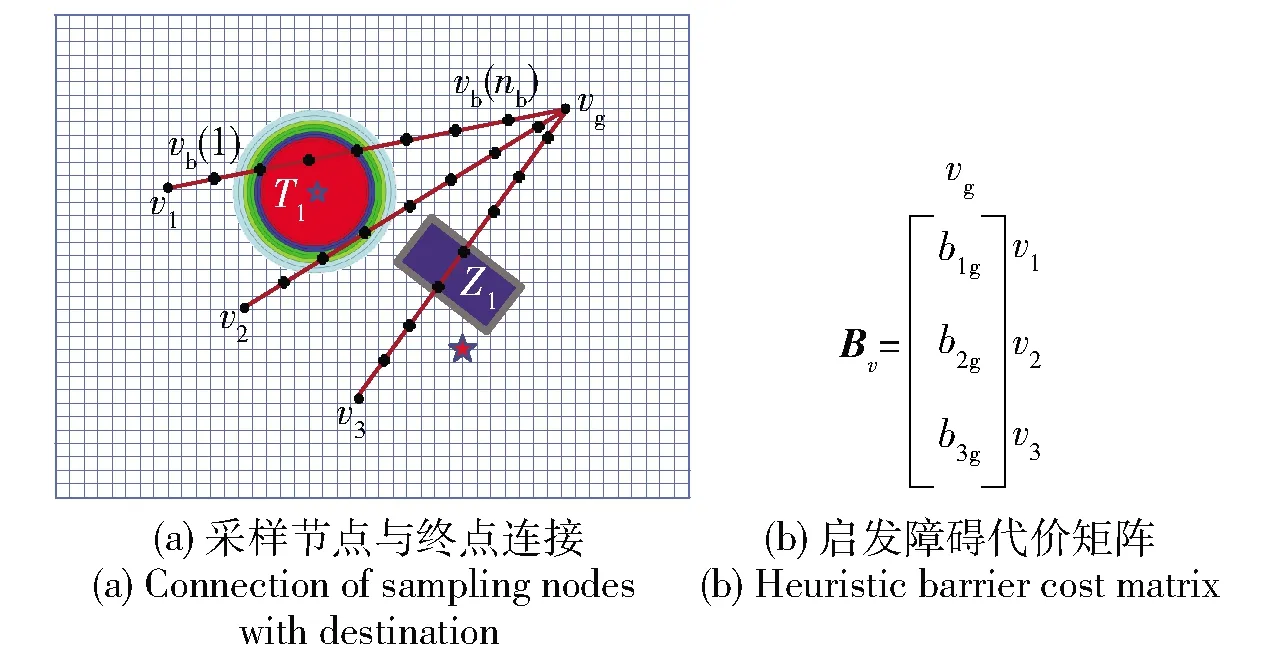
图8 越野环境采样节点和终点连接与启发障碍代价矩阵
启发距离代价矩阵Hv由集合V中节点vi与目标终点vg之间欧式距离dig构成,其计算方法如(12)式所示:
dig=‖vi-vg‖.
(12)
节点vi与目标终点vg之间路段的通行距离评估用启发距离代价矩阵表示,如图9(a)、图9(b)分别表征包含障碍物Z1、环境威胁T1的越野环境及其对应的启发距离代价矩阵。
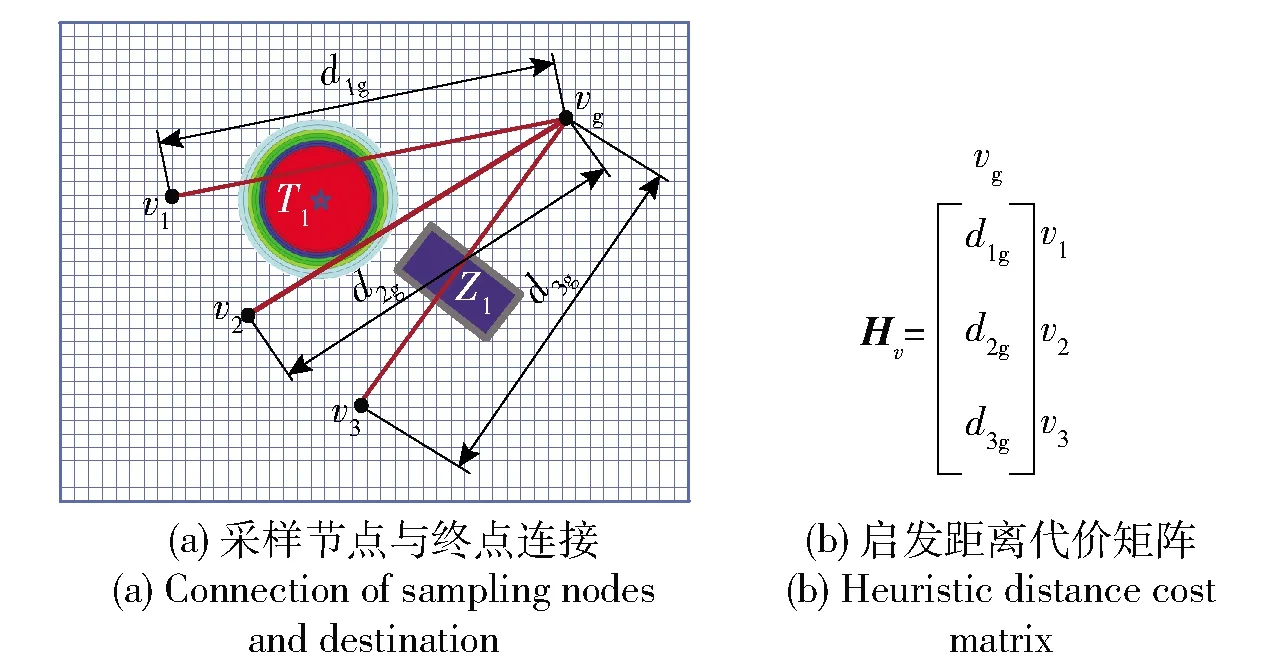
图9 越野环境采样节点和终点连接与启发距离代价矩阵
启发道路代价矩阵Mv由集合V中节点vi与目标终点vg之间的启发道路代价pig构成。通过在采样节点与终点间的路段中各子节点vr(1)~vr(n)所在的道路层势能场累加和来评估,如(13)式所示:
(13)
节点vi与目标终点vg之间路段的通行道路评估用启发道路代价矩阵表示,如图10(a)、图10(b)分别表征包含越野道路P1、P2的越野环境及其对应的启发道路代价矩阵。
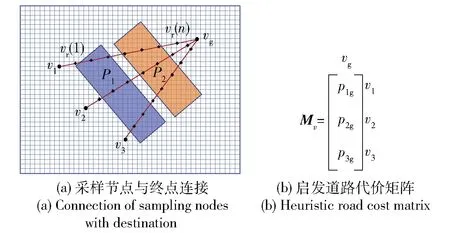
图10 越野环境采样节点和终点连接与启发道路代价矩阵
2.2 在线路径优化
在线路径优化方法采用通行代价评估函数来优化路径,如(14)式所示:
F(vi)=q(vi)+h(vi),
(14)
式中:F(vi)为由从起始点(即源节点vo)到当前节点vi的通行代价评估函数;q(vi)为从源节点vo到当前节点vi的扩展代价评估函数;h(vi)为当前节点vi到目标点vg的启发代价评估函数。
2.2.1 节点扩展
节点扩展是在越野环境拓扑图G中从当前节点vi向周围节点连接,节点扩展法具有搜索路径优化程度高的优点,并且能提高路径规划速度。节点扩展方法如图11(a)所示,首先按连通矩阵由源节点vo出发扩展至可行连通节点vi,如vo与vi之间连接路径aoi可行,生成候选节点集合Q={vi|vi∈V,aoi=1},在Q集合中搜索通行代价最小的优化节点vmin,再由该节点出发扩展至其周边的连通节点,并将新扩展节点加入集合Q,如此往复循环,直至扩展至目标终点vg.
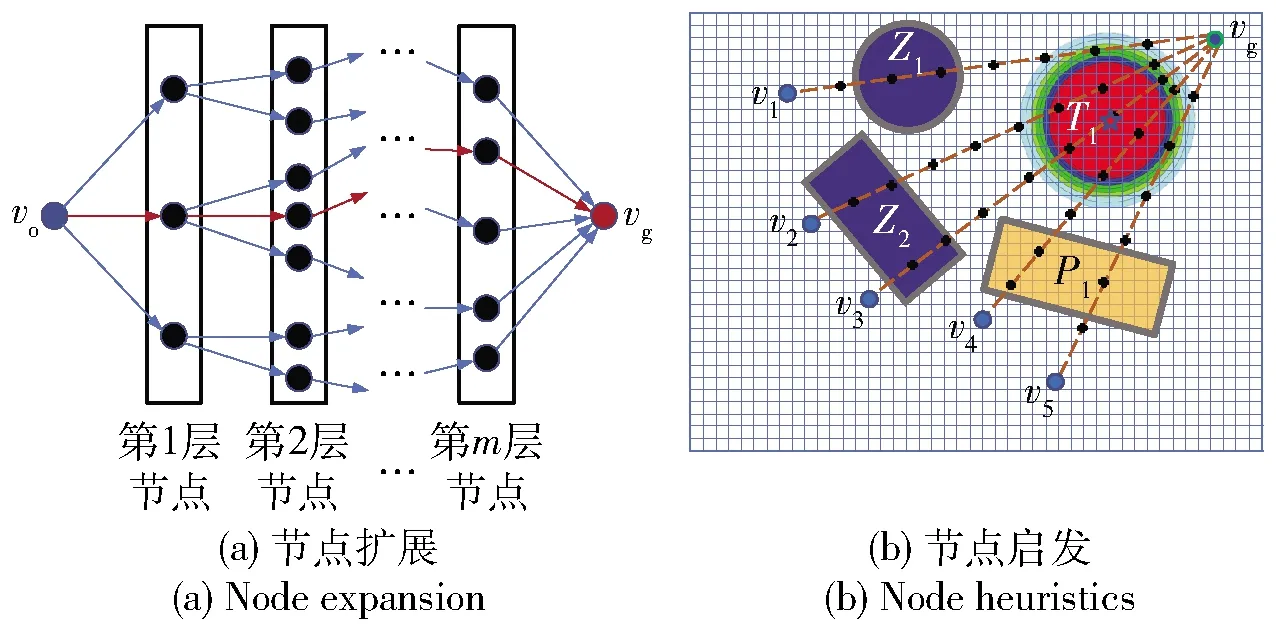
图11 APF-PRM算法节点扩展与启发方法
节点扩展过程中,对于新扩展节点,使用扩展代价评估函数,通过加权计算,评估由源节点至该节点的扩展代价,如(15)式、(16)式所示:
q(vi)=q(vmin)+qi,
(15)
qi=fd·dij+fs·sij+fr·pij,
(16)
式中:q(vmin)为由源节点vo至节点vmin的扩展代价;qi为节点vmin到vi间的扩展代价;fd、fs和fr分别为距离权重系数、安全权重系数和道路权重系数。
2.2.2 节点启发
为提高路径规划效率,优化节点扩展方向,需要考虑新扩展节点vi与目标终点vg间的启发代价,并优先由启发代价最小的方向进行路径搜索。
节点启发代价方法如图11(b)所示,环境中包含有2片障碍物Z1~Z2、1处环境威胁T1和1片越野道路区P1.设候选节点集合Q中包含v1~v5新节点,采用启发代价评估方法,分别计算启发障碍代价、启发距离代价和启发道路代价,通过加权计算,评估该节点至终点的启发代价,如(17)式所示:
h(vi)=fb·big+fd·dig+fr·pig,
(17)
式中:h(vi)为新扩展节点vi与目标终点vg间的启发代价评估函数;fb为障碍权重系数;big、dig和pig分别为启发代价评估矩阵中节点vi的启发障碍代价、启发距离代价、启发道路代价。
2.2.3 路径优化
如图12所示,APF-PRM算法在路径优化初始化阶段生成备选节点集合Qc、候选节点集合Q和优化节点集合C,并将起始点vo加入集合Q中。
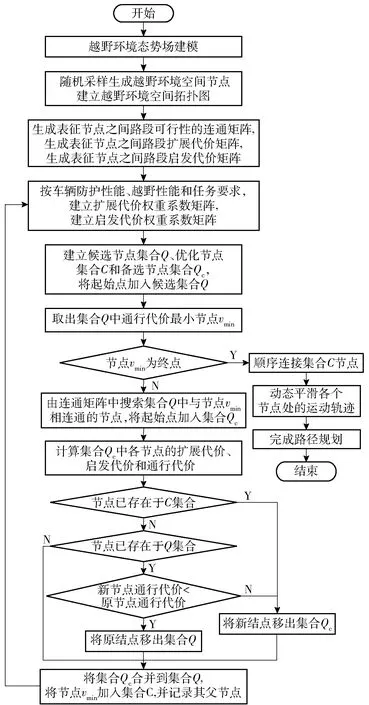
图12 APF-PRM算法流程
在路径优化过程中,不断地重复以下步骤,直到目标终点vg进入优化节点集合C中:
1)取集合Q中通行代价最小节点为当前优化节点vmin,如(18)式所示:
(18)
2)利用连通矩阵Av,搜索集合V中与vmin相连通的节点vi,并将其加入集合Qc;用扩展代价评估矩阵Sv、Dv、Pv和启发代价评估矩阵Bv、Hv、Mv,以及对应的权重系数,计算其扩展代价q(vi)、启发代价h(vi)和通行代价F(vi),并记录其父节点信息vmin.
3)检查集合Qc中的各个节点vi,如该节点已在集合C中,则将该节点移出集合Qc.如该节点已在集合Q中,则比较集合Qc和Q中同一节点的通行代价F′(vi)和F(vi):若F′(vi)
4)将集合Qc与Q合并。将其上一级优化节点vmin加入到集合C中,并记录其父节点。
5)如当前节点vmin为目标终点vg,则说明已找到优化路径节点序列,由vmin出发,按集合C中各节点的父节点链表信息顺序连接,即为优化路径;否则返回到步骤1,继续搜索优化路径。
2.2.4 轨迹优化
优化路径节点顺序连接后,得到车辆运动轨迹由多段折线构成,如图13中红色虚线,由于轨迹在节点处存在硬拐点,无法满足车辆运动学约束要求,本文采用动态曲率平滑法优化车辆运动轨迹。首先设定车辆最小转弯半径Rmin和理想转弯半径为Ri,在轨迹优化时,首选以Ri为半径在节点处规划车辆运动轨迹,见图中的蓝色细实线,vt(1)、vt(4)、vt(5)和vt(6)分别为两段曲线与直线轨迹之间的切点,如轨迹与障碍或威胁发生干涉(如图13中障碍Z1与其周边蓝色细实线轨迹干涉),说明该轨迹不可行,则按(19)式减小转弯半径,生成新的车辆运动轨迹,直至消除干涉(如图13中Z1周边的黑色粗实线平滑轨迹,vt(2)和vt(3)为新生成曲线与直线轨迹之间的切点)。如减小至最少转弯半径Rmin时仍不能避免干涉,则需要对该段路线重新规划。
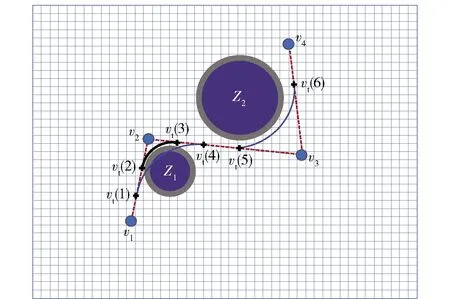
图13 路径平滑方法
R=Ri-λR(Ri-Rmin),λR∈(0.1,0.5).
(19)
综上所述,APF-PRM算法由4部分组成:第1部分为环境建模,即通过获取的环境感知信息,在栅格化越野环境中生成多层次环境态势场模型;第2部分为离线采样学习,通过随机采样法生成越野环境拓扑图,建立节点之间的连通矩阵和多维度通行代价评估矩阵;第3部分为在线路径优化,首先根据车辆性能和任务要求建立代价权重向量,然后从起始点出发进行节点扩展,扩展过程中通过评估节点扩展代价和启发代价,搜索候选节点集合中通行代价最优的可行节点,直至到达目标终点;第4部分为轨迹优化,按照车辆的运动学特性,采用动态曲率平滑法优化各节点处的车辆运动轨迹。
3 仿真实验
为验证算法的有效性,本文在模拟越野环境中完成了路径规划,并通过仿真对比实验验证了APF-PRM算法的可行性和综合性能的优越性。
3.1 实验参数设置
APF-PRM算法通过权重向量设置来进行个性化路径规划,包括扩展权重向量ke=[fsfrfd]和启发权重向量kh=[fbfrfd],权重系数由车辆防护、越野性能、任务要求,以及环境障碍、威胁和越野道路的分布决定。本文按专家经验法以及仿真实验所得的数据分析,确定权重系数在[1,10]范围,具体权重系数选择如表2所示。
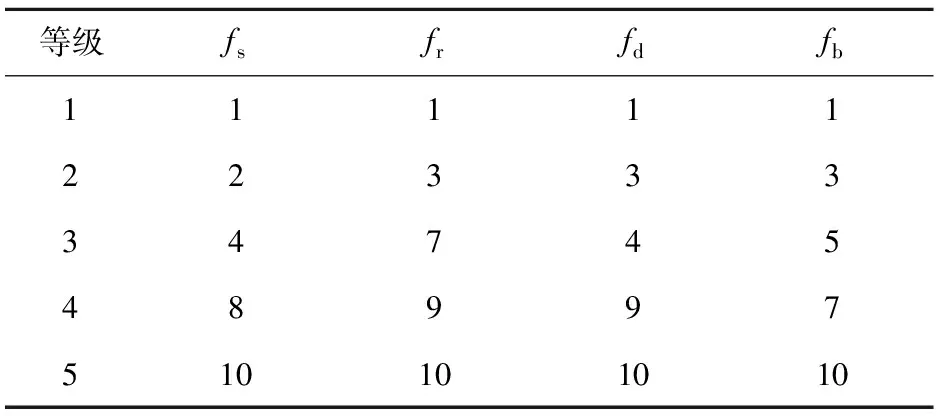
表2 APF-PRM算法路径规划权重系数
3.2 路径规划仿真
为验证APF-PRM算法性能,在模拟越野环境(1 002 m×1 114 m)下进行路径规划,并将规划结果与PRM、RRT、A*、APF算法进行对比。图14(a)、图14(b)为APF-PRM算法按两组不同的权重向量所规划的路径。当车辆的防护、越野能力弱,在非紧急任务条件下,取权重向量ke=[1,1,1]、kh=[1,1,1],由图14(a)可知,规划路径能够避开障碍物、环境威胁和越野道路区到达目标终点;当车辆具备较强的防护、越野能力,在非紧急任务条件下,取权重向量ke=[10,10,1]、kh=[10,10,1],由图14(b)可知,规划路径能够避开障碍物,穿过环境威胁作用范围边缘和越野道路区,取捷径到达目标终点。
图14(c)~图14(f)所示分别为PRM、RRT、A*、APF算法规划路径,由图可知,4种算法都具有避障功能,并具有各自的优点,相比而言APF-PRM算法的优势在于:1)通过环境态势建模识别环境威胁和越野道路,能够避免车辆从威胁影响区和越野区中通过,造成安全风险;2)通过势能场模型来避开障碍物边缘,规避碰撞风险;3)通过路径平滑模块,解决硬拐点和曲率半径过小的问题,规划的路径符合车辆运动学特性;4)能够通过车辆特性和任务要求的权重向量设置来进行个性化路径规划。
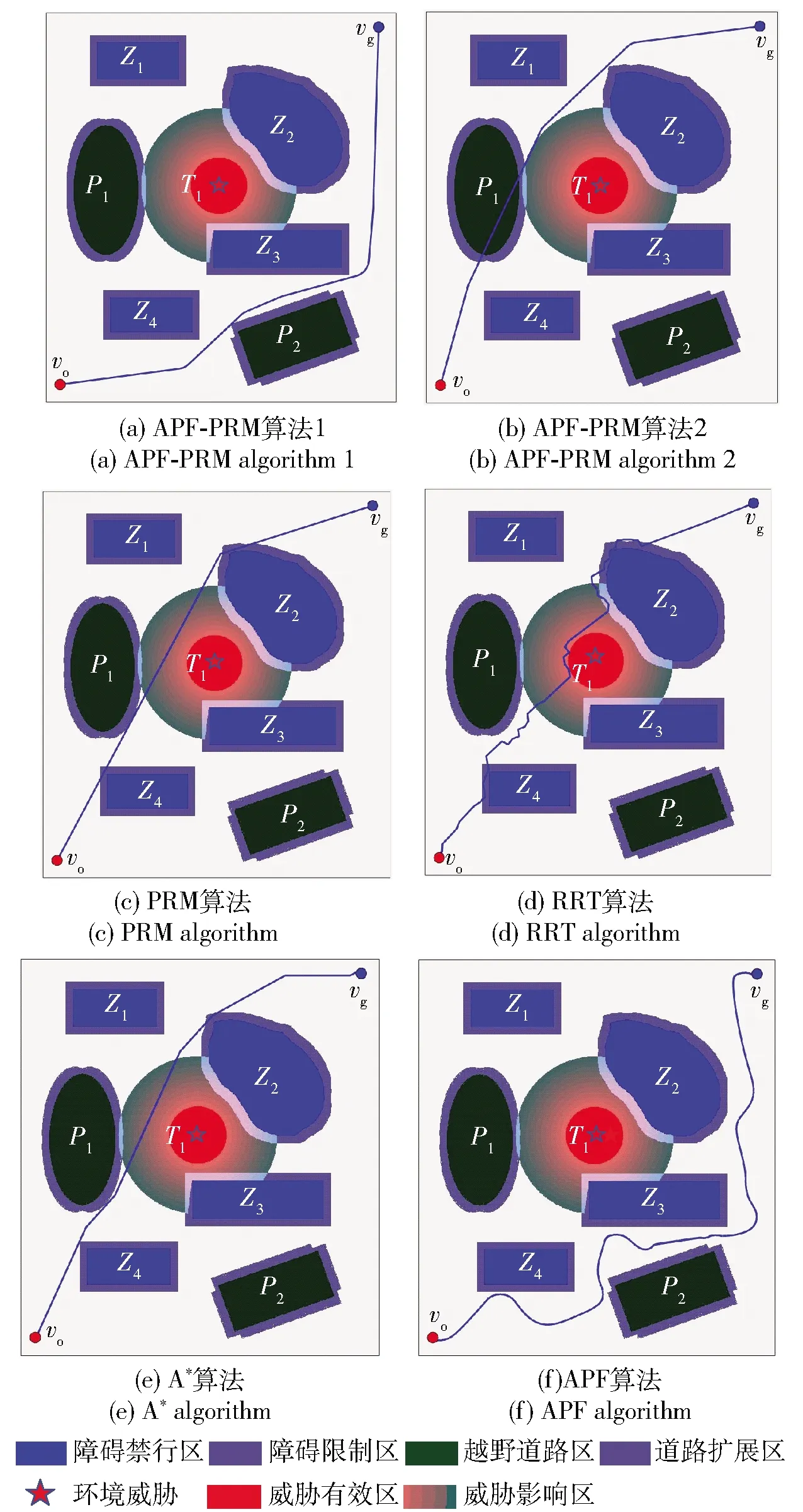
图14 路径规划算法对比
APF-PRM算法与4种算法性能指标对比如表3所示。由表3可知,APF-PRM算法考虑多种越野环境因素影响,并进行环境态势场建模,因而规划时间略长,规划路径时避开了威胁要素的影响和越野区域,故路径距离略远,但车辆行驶的安全性高,生成的路径符合车辆动力学要求,因此其综合性能较优。
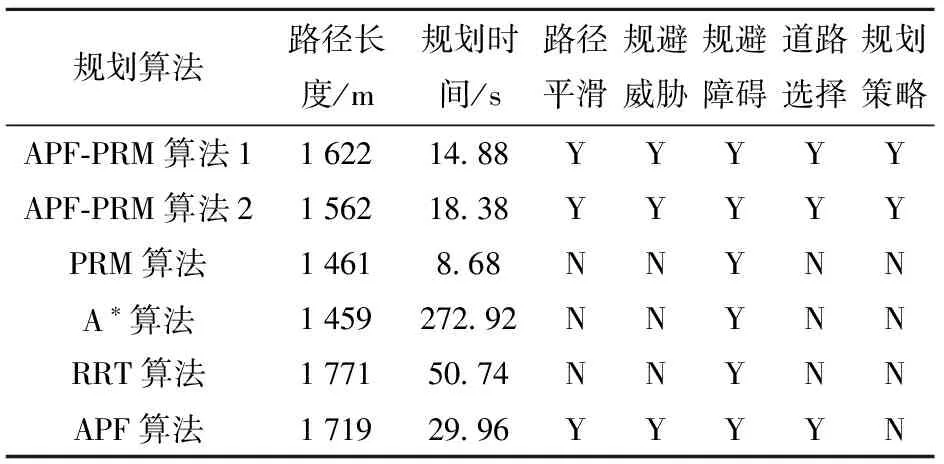
表3 路径规划算法对比
与4种规划算法对比,APF-PRM算法在基本避障功能基础上,具备规避环境威胁和越野道路能力,规划轨迹符合车辆运动学要求,并能够根据车辆的防护、越野性能,以及任务要求调整车辆路径规划策略。因此,APF-PRM算法在特定的越野环境下,其规划路径在可行性、安全性、规划速度、个性化程度方面具有一定综合优势。
为验证APF-PRM算法可行性,在多种场景下进行了路径规划仿真实验。以场景A(2 324 m×686 m)和场景B(2 296 m×1 027 m)两种越野环境为例,使用不同的权重向量进行路径规划,所得到的路径如图15和图16所示。由图15和图16可见,该算法能够根据车辆性能和任务需求,按照权重向量合理规划路径。
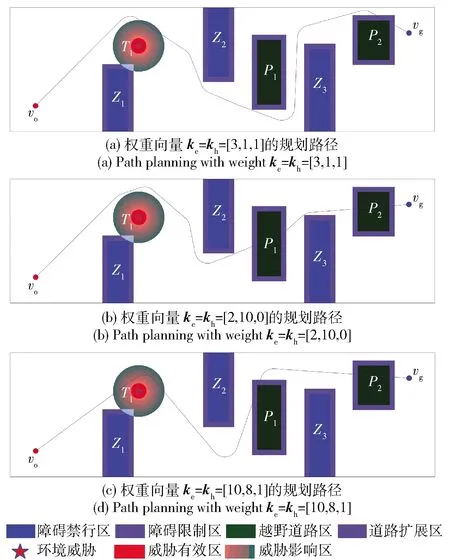
图15 场景A环境条件下多权重路径规划对比
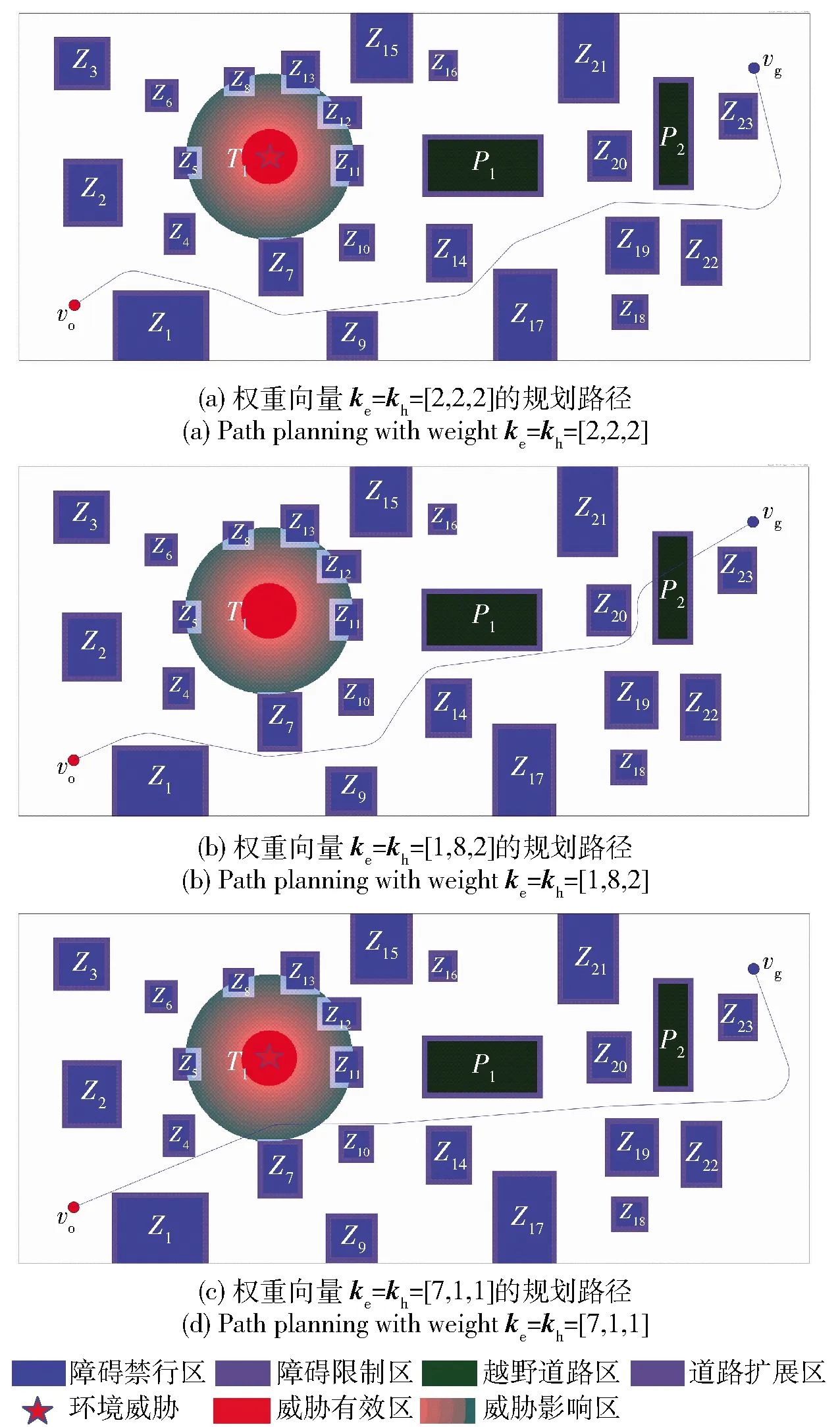
图16 场景B环境条件下多权重路径规划对比
5 结论
本文基于APF方法对越野环境建模,在车辆行驶量化风险评估的基础上,提出一种改进的PRM路径规划算法,满足越野环境条件下规划安全可行路径的需求。得出以下主要结论:
1)本论文提出一种结合APF模型与PRM方法的路径规划框架结构。建立基于APF方法的多层次环境态势场模型,通过对越野环境中的障碍物、环境威胁和越野道路进行层次化势能场量化建模,将其融合为环境态势场,实现了复杂越野环境下车辆行驶量化风险评估。
2)提出基于环境态势场的可行性和安全性节点连接路径评估模型。基于PRM方法进行节点采样,建立采样节点间可行性评估连通矩阵和多维度通行代价评估矩阵。以可行节点间通行代价为优化指标,按节点扩展与启发综合方法规划路径;采用动态曲率平滑法,优化车辆运动轨迹,解决复杂越野环境条件下的智能车路径规划问题。仿真实验结果表明APF-PRM算法考虑了越野环境中多种因素的综合影响,以及车辆的性能特点和任务要求,能在越野环境条件下,规划安全可行的行车优化路径。
