多目标时空同步协同攻击无人机任务分配与轨迹优化
2021-08-27张云飞林德福郑多程子恒唐攀
张云飞,林德福,郑多,程子恒,唐攀
(北京理工大学 宇航学院, 北京 100081)
0 引言
面向现代局部战争的新要求,无人机应用场景由广阔战场环境向复杂城市环境发展[1]。旋翼无人机(巡飞弹)由于其在城市环境具有悬停、垂直起降、便携性等独特的优势,受到广泛关注,如以色列的“萤火虫”、“罗特姆”旋翼巡飞弹、欧洲GLMAV新概念巡飞弹、波兰的“蜻蜓”巡飞弹等。与此同时,打破传统单机执行任务的局限,利用数架无人机对多目标协同打击,能够有效提升毁伤效能和突防概率,将成为未来战争中一种重要的作战模式[2-4]。因此,研究旋翼无人机复杂作战环境下的多目标协同打击问题具有现实意义。
多目标协同打击问题可以描述为复杂多约束条件下的多目标任务分配和轨迹规划两个子问题。任务分配是指考虑多目标任务和战场态势,对每架无人机的打击目标进行优化配置,使其以最小代价协作完成任务;轨迹规划是考虑地形、气象等环境因素,在满足彼此协同、外界环境和无人机自身等约束条件下,在任务分配的基础上对无人机从初始位置到目标位置的最优飞行路径进行规划[5-7]。多目标分布式协同打击问题融合了任务分配和路径规划两个问题,其数学描述复杂,过程和终端约束条件多,导致优化求解难度大。
多目标任务分配是协同攻击的前提,合理的任务分配是综合火力打击、能量消耗、时间等因素的最优配置。任务分配常用模型有多旅行商问题模型[8-9]、混合整数线性规划模型[10-12]、合同拍卖网模型[13-14]。多旅行商问题是经典旅行商问题的拓展,且在无人机任务分配上有广泛的应用[8]。Kivelevitch等[9]建立经济模型解决多旅行商(MSTP)问题,通过多个代理商综合考虑收益与路径因素,获得任务分配的最优解。混合整数线性规划模型,文献[10]对典型的对敌防空压制(SEAD)任务场景,设计了一种基于整数编码混合遗传算法进行任务分配的方法。文献[11]提取障碍物的有效节点,采用混合整数的方法解决无人机对动目标的任务分配问题。文献[12]采用混合整数方法实现了线上动态任务分配与轨迹规划算法。关于拍卖网模型,由Bertsekas[13]首先提出拍卖算法,并解决了单任务分配问题;严飞等[14]在考虑约束情况下,利用合同网协议实现异构无人机实时任务分配。针对某些特定的实际情况也衍生出来不同的算法,Manyam等[15]提出了一种长机和僚机的协作攻击模式,通过利用僚机对威胁进行探测来降低长机的威胁,采用Voronoi图进行地图划分并以此为路径进行搜索。
时空同步攻击是提升突防概率的重要手段,亦是多机协同实现效能倍增的关键。针对时空同步攻击问题,现有研究主要包括两种研究思路,一种是在规划路径的基础上,通过调整路径或调整无人机的飞行速度来实现时间上的协同。Chandler等[16]通过调节无人飞行器的速度,从而保证多飞行器在时间上的合理安排;Beard等[17]通过调整部分无人飞行器的航迹长度,实现无人飞行器同时到达任务区域;文献[18]提出一种用于多无人机避碰的轨迹生成办法,并实现了线上动态时间协调。另一种实现时空同步攻击的方法是在动力学约束下,将时间作为控制因素加入轨迹规划中,针对无人机的可行轨迹通过构造无人机的飞行轨迹函数实现。Bellingham等[19]应用混合整数线性规划法解决了有时间限制的紧密耦合问题,该方法的优点是得到最优值,但计算量大,不适合在线规划。张思宇等[20]提出基于时间约束集的发射时间规划算法框架,建立了以发射时间为优化变量、避免飞行碰撞为约束条件和同时到达目标为优化目标的优化问题,但是每条轨迹的运算时间不同,存在时间较长的情况,且不能严格实现同时达到的目标。Eun等[21]通过遗传算法(GA)实现多任务分配,并将时间作为约束以实现协同攻击,但是假设速度为恒定的速度,且只是任务层规划。
本文面向复杂战场环境下多目标协同打击的需求,研究了存在多禁飞区约束的复杂环境下,多目标的分布式时空同步协同打击问题。考虑多个禁飞区域约束,本文基于Delaunay三角形构建可行飞行路径地图,利用A*算法研究单无人机路径搜索策略,保证无人机规避禁飞区。为了对无人机打击目标进行优化配置,利用sigmoid饱和函数增大数值敏感度,提升任务分配的最优性。在此基础上,提出基于贝塞尔曲线的无人机轨迹连续性约束方法,通过引入动态时间调节因子,实现分布式无人机时空同步到达的路径规划。进一步考虑噪声、阵风等干扰条件,研究无人机的协同轨迹跟踪控制问题。本文提出的多无人机协同打击策略,赋予无人机在多约束、高动态复杂战场环境下的时空同步协同打击能力,提升了无人机协同突防作战的任务效能。
1 无人机协同打击问题数学描述
1.1 协同打击问题
在存在多个禁飞区域(如障碍物、敌方探测雷达、火力点等)的典型作战区域中,为了尽可能地实施突防,增大毁伤效能,利用多架无人机对多个目标进行时空同步协同打击,如图1所示。
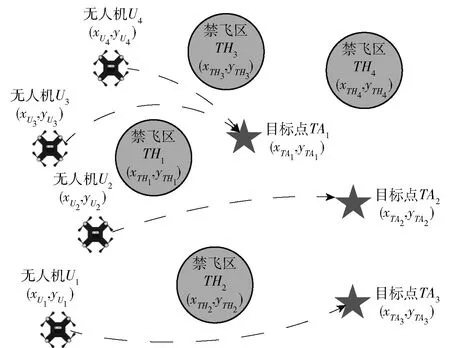
图1 多机协同作战场景
任务场景中含有多个打击目标TAi、若干障碍物THj,其中xUk为第k架无人机的位置坐标,xTHj为障碍物THj中心点位置坐标,xTAi为第i个打击目标位置坐标。多目标分布式协同打击包含两个子问题:
1)多目标任务分配。多目标任务分配是对无人机资源的配置,通过给每架无人机分配合理的任务目标,以尽可能最小的代价完成多目标打击。代价函数可表示为
(1)
式中:uU为无人机数量;nTA为目标点数量;αk,j为分配系数,αk,j∈{0,1},1表示无人机Uk执行TAi任务,0表示不执行TAi任务;f(LUkTAi)为路径的代价函数,LUkTAi为无人机Uk到目标点TAi的飞行路径。约束条件保证了每架无人机仅执行一个任务。
2)时间约束的路径规划与跟踪。时间约束的路径规划与跟踪是无人机协同执行任务的核心,以实现时空同步打击多个目标,最大化打击效能,即
(2)
式中:Lk为第k架无人机的轨迹;F(Lk)为每条路径的优化函数;tk为第k架无人机的时间,保证无人机规划轨迹的最优性;Ts为预先设定的时间。通过该约束条件可保证每条飞行轨迹所需时间都相等,且为预设定的时间Ts.
1.2 无人机动力学模型
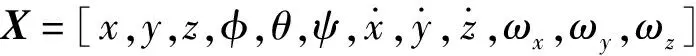
牛顿等式为
(3)
式中:m为无人机质量;g为重力加速度。
欧拉等式为
(4)
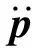
对无人机12个状态量进行简化,选取其中的部分状态量,并通过部分状态量及部分状态量导数将所有其他的状态量表达出来,最终可以得出无人机系统的平坦输出[22]为
σ=[x,y,z,ψ].
(5)
(6)
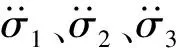
进一步建立一个中间坐标系Ocxcyczc,中间坐标系Ocxcyczc与机体坐标系Obxbybzb之间只存在俯仰和滚转角的差别,中间坐标系Ocxcyczc的Ocxcyc平面与世界坐标系Owxwywzw的Owxwyw平面共面,如图2所示。根据坐标系的定义以及坐标系之间的关系,可以得到中间坐标系x轴方向单位矢量和y轴方向单位矢量的表达方式:
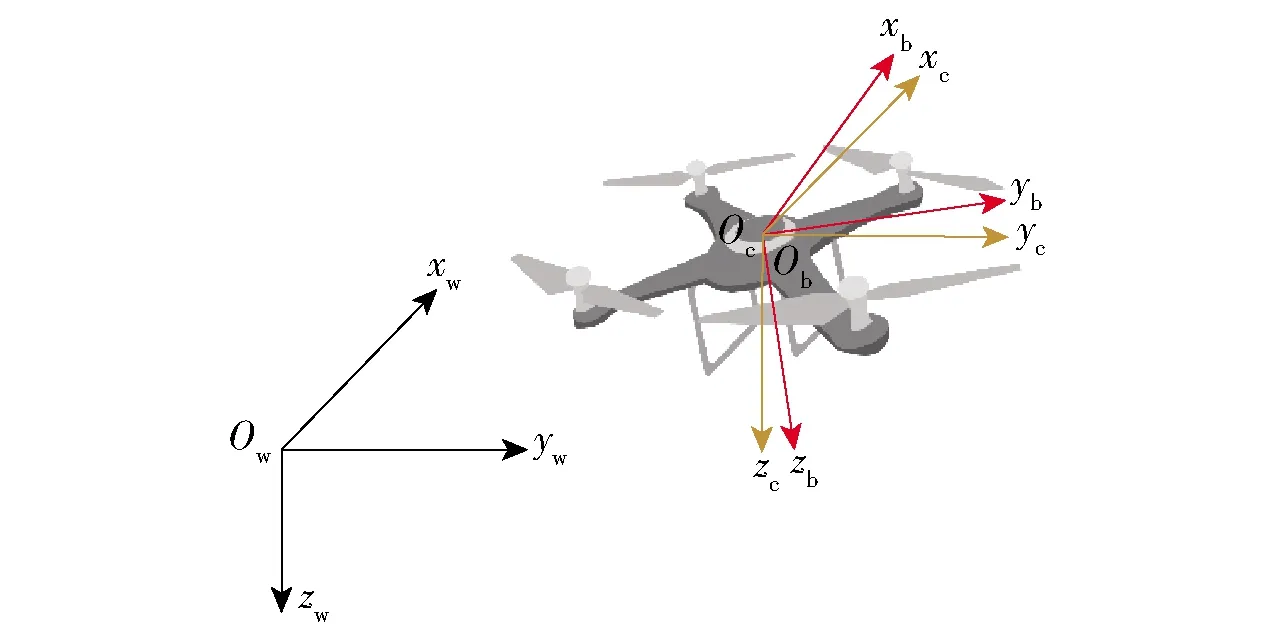
图2 坐标系转换关系
(7)
式中:σ4为平坦输出的第4个输出量。
通过(6)式、(7)式,可以唯一求解出无人机姿态,即惯性坐标系和机体坐标系的转换矩阵:
(8)
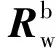
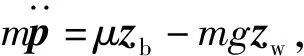
(9)
式中:a为无人机加速度;ωbw为机体坐标系相对于惯性坐标系的旋转角速度。
为了便于后续公式的表达,定义变量hω为
(10)
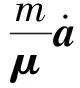
最终可以推导得到旋转角速率[ωx,ωy,ωz]为
(11)
通过上述的推导可知,无人机全部状态均可由x、y、z、ψ4个状态量进行表示,因此对无人机的路径规划即是对[x,y,z,ψ]4个状态量进行规划。
2 单无人机路径图构建及其搜索策略
单机的飞行路径安全是多无人机协同规划的前提,因此本部分首先研究多禁飞区约束下的单机路径规划问题。
2.1 基于Delaunay三角形的搜索地图构建
Delaunay三角形存在空圆特性和最大化最小角性质[23-25],可以将地图划分成最小单元,保证飞行路径有效规避禁飞区,因此可基于Delaunay三角进行战场环境地图构建。
选取无人机U1,终点目标TA1,禁飞区中心位置TH={TH1,TH2,…,THq}。生成算法采用Bowyer-Watson算法,即:
1)构造一个超级三角形,包含所有禁飞区,放入三角形链表。
2)将禁飞区中的散点依次插入,在三角形链表中找出其外接圆包含插入点的三角形(称为该点的影响三角形),删除影响三角形的公共边,将插入点与影响三角形的全部顶点连接起来,从而完成一个点在Delaunay三角形链表中的插入,如图3所示。
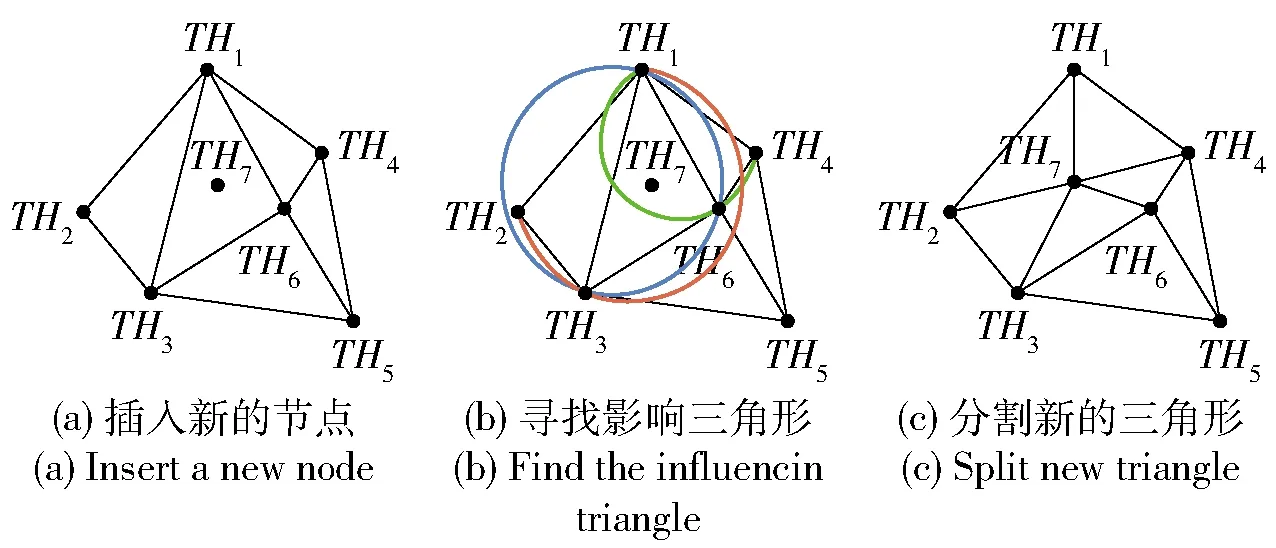
图3 Bowyer-Watson算法
3)循环执行上述第2步,直到所有散点插入完毕。
根据Bowyer-Watson算法,可建立搜索地图如图4所示。

图4 基于Delaunay三角形的地图构建
为了尽可能增大飞行安全性,取三角形边线的中点为路径点,将初始位置和最近的三角形中点相连作为初始搜索路径,将终止位置和最近的3个三角形中点相连作为终止搜索路径,可建立搜索树地图,如图5和图6所示,图中P1,P2,…,P19表示搜索树节点。
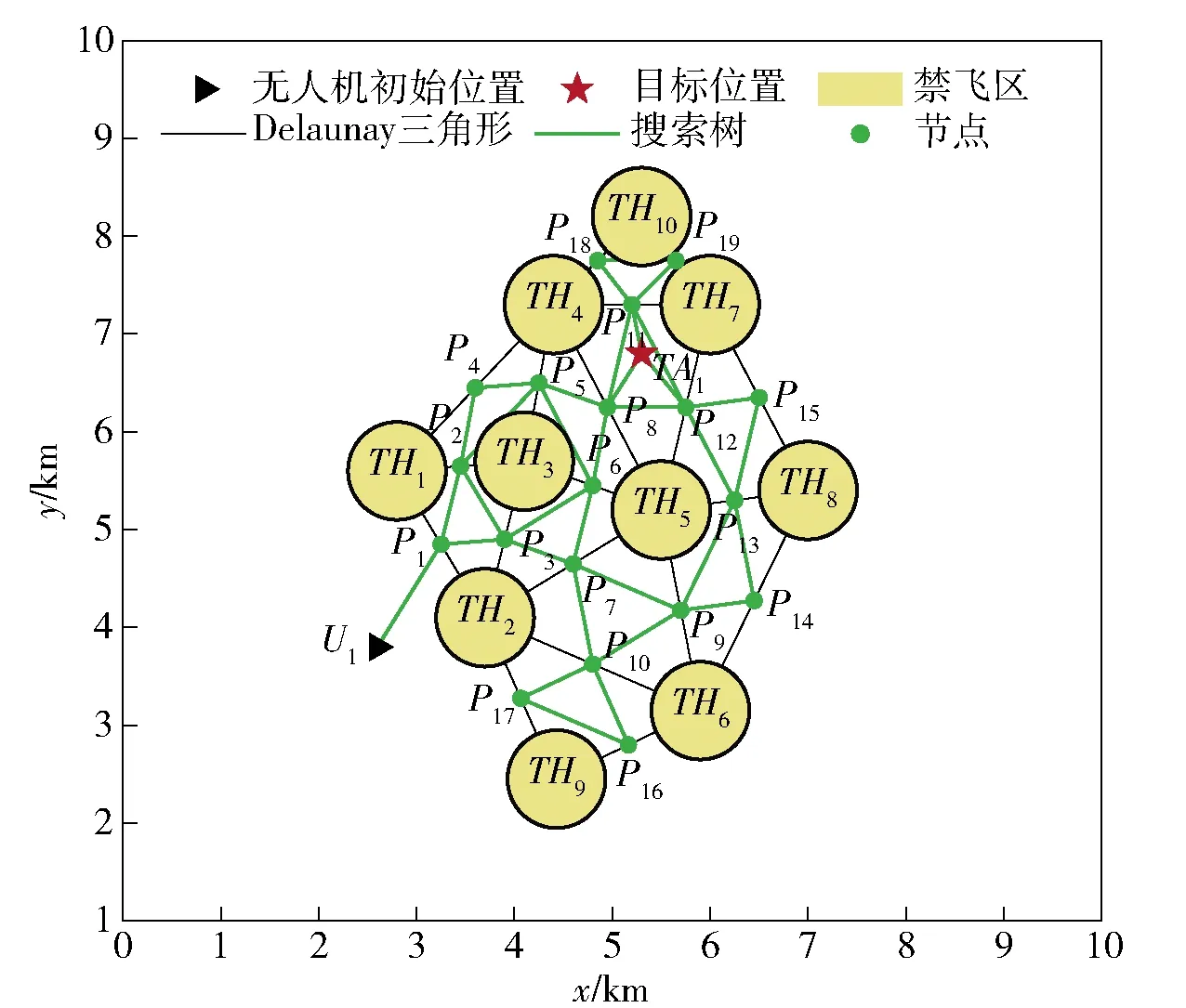
图5 搜索树
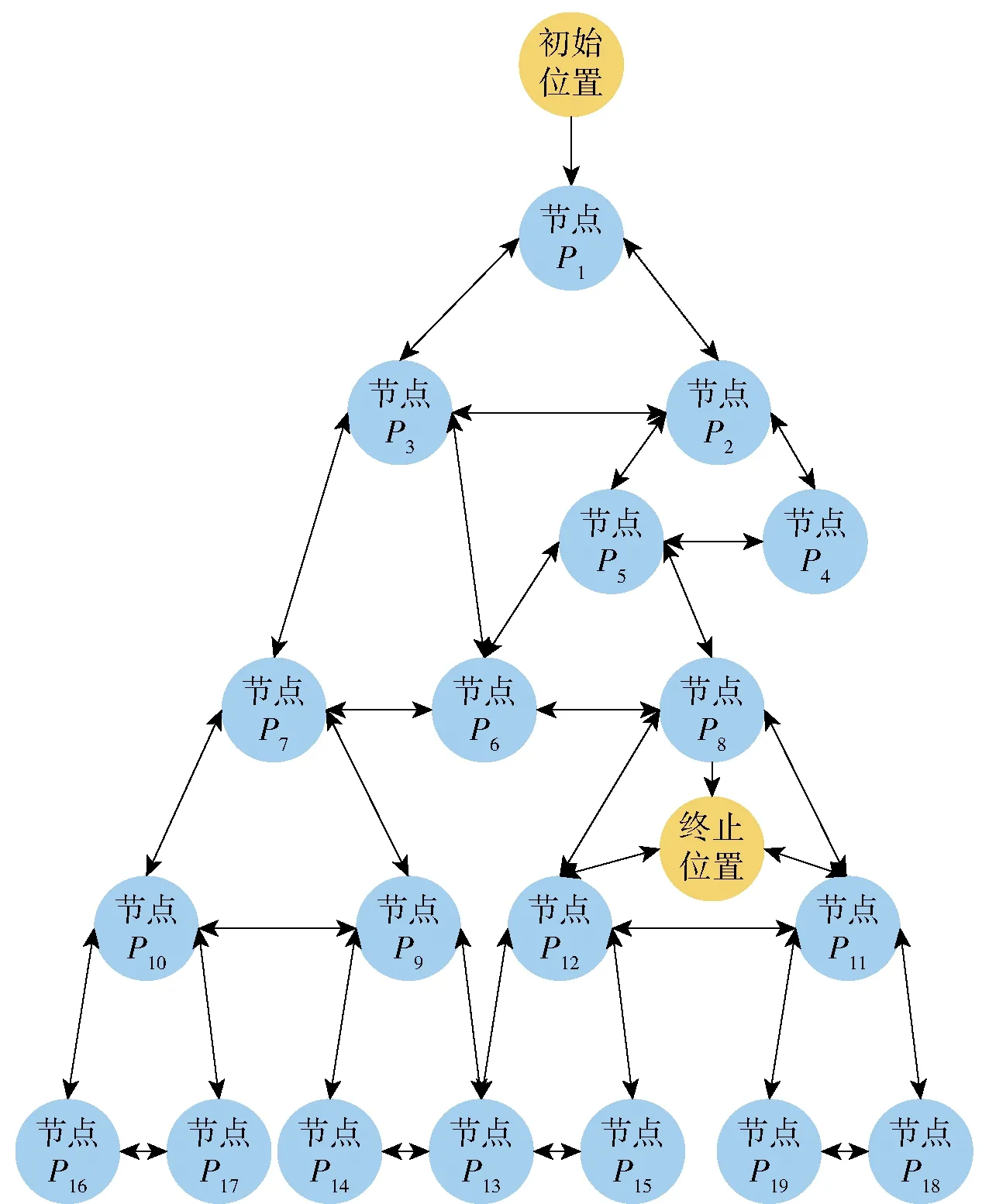
图6 搜索树节点示意图
2.2 A*路径搜索
为了在诸多可行路径中搜索出满足性能指标最优的飞行路径,采用A*启发式搜索算法。设定代价函数表达式为
f(n)=g(n)+h(n),
(12)
式中:g(n)为节点转移的代价函数;h(n)为启发式搜索函数。
代价函数和启发式函数可描述为
g(n)=αdn,n+1,
(13)
式中:α是归一化参数,使得g(n)满足g(n)∈[0,1];dn,n+1表示节点n和节点n+1之间的距离。
轨迹的安全性是无人机任务的前置条件,综合考虑整条轨迹的相对安全性与轨迹的绝对安全性,将节点n和节点n+1之间的点划分成N份,求N个节点到单个障碍物之间的最小距离,并选取最小距离为代价函数评估轨迹的相对安全性。在此基础上,增加判定条件如下:如果最小距离小于设定的安全半径,将最小距离设定为0.1 m.以此判定条件来保障路径的绝对安全,如图 7所示。综上可以得到启发式搜索函数为
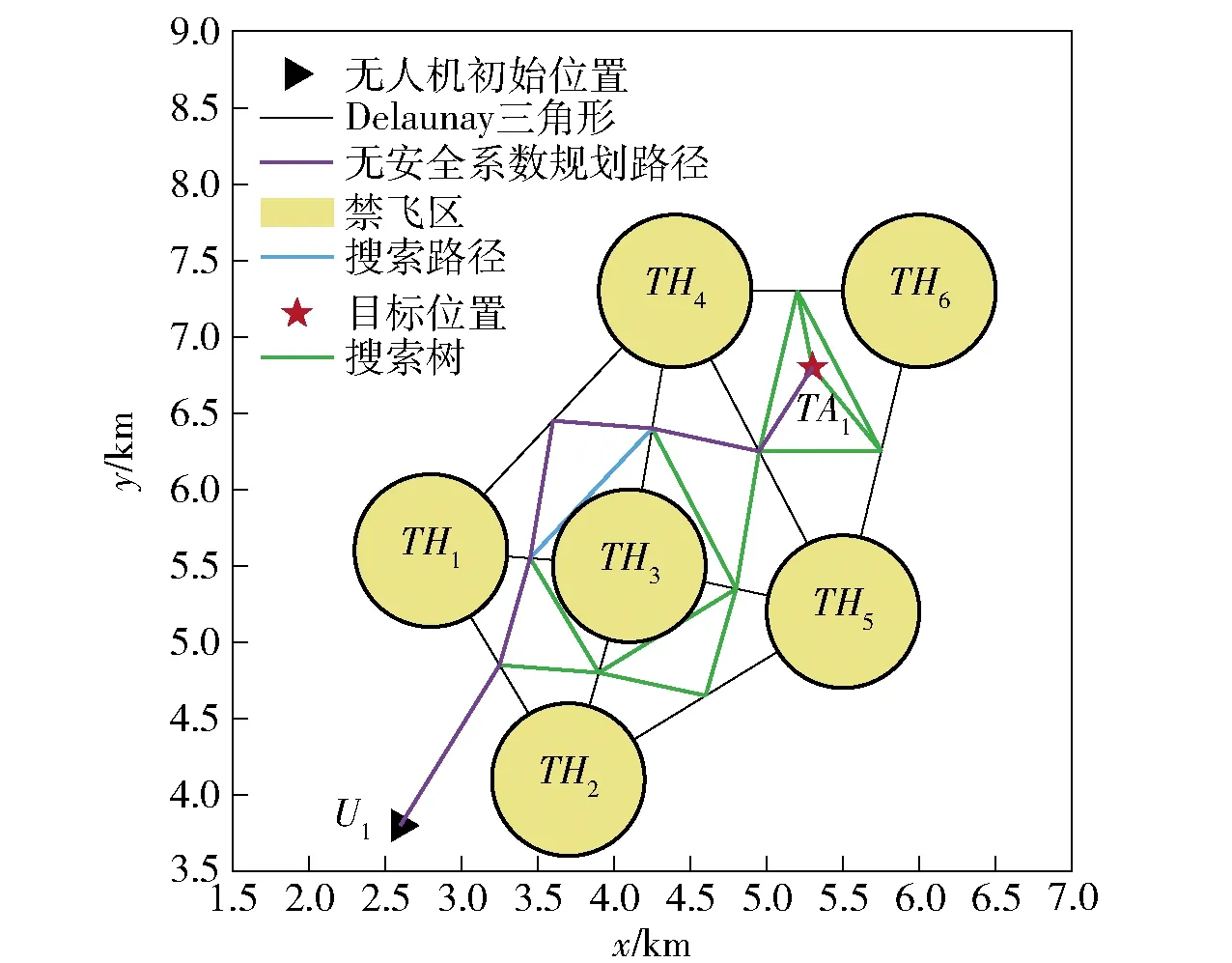
图7 轨迹安全性
(14)
式中:β是参数归一化因子,使得满足h(n)∈[0,1];nTH为障碍物数量;dTHj,l表示节点n与拓展节点n+1之间的第l个点与THj禁飞区之间的距离。
通过启发式的搜索可以找到一个从起点到终点的路径,并且满足
∑f(n)→min,
(15)
如图8所示,从无人机初始位置点经过点p1、p3、p6、p8到达目标点位置的一条路径。
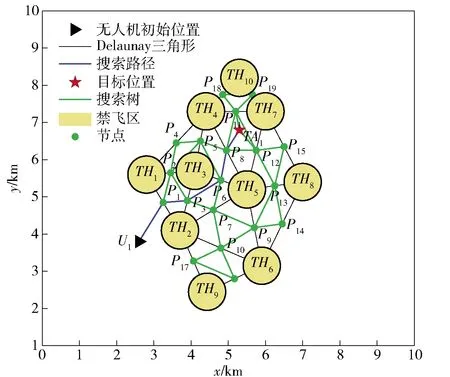
图8 A*算法路径搜索结果
3 多目标协同攻击任务分配
为了以尽可能小的能量损耗实现多目标协同打击,需要对多个目标进行优化分配。将能量损失、威胁因子、打击力度和无人机分布情况作为目标分配的综合考量因素,构造代价函数f({Uk},{TAi},{THj})。
定义代价函数f({Uk},{TAi},{THj})为
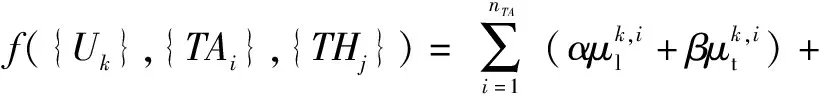
μf[i1,…,inTA]+μs[i1,…,inTA],
(16)
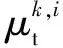
(17)
式中:m(i)表示攻击同一个目标的无人机数量。
(18)
式中:n(TA)表示攻击目标个数。
为了最小化代价函数f({Uk},{TAi},{THj}),可通过给每个无人机分配对应的目标点来获得无人机的分布,其优化模型则可表示为
(19)
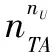
为了实现多方向打击目标,需要在保证飞行安全约束条件下,为相同攻击方向的目标提供额外的可行打击方向。基于已经建立的搜索树,得到连接目标的3个节点为{Pa,Pb,Pc},目标节点的搜索树如图9所示。
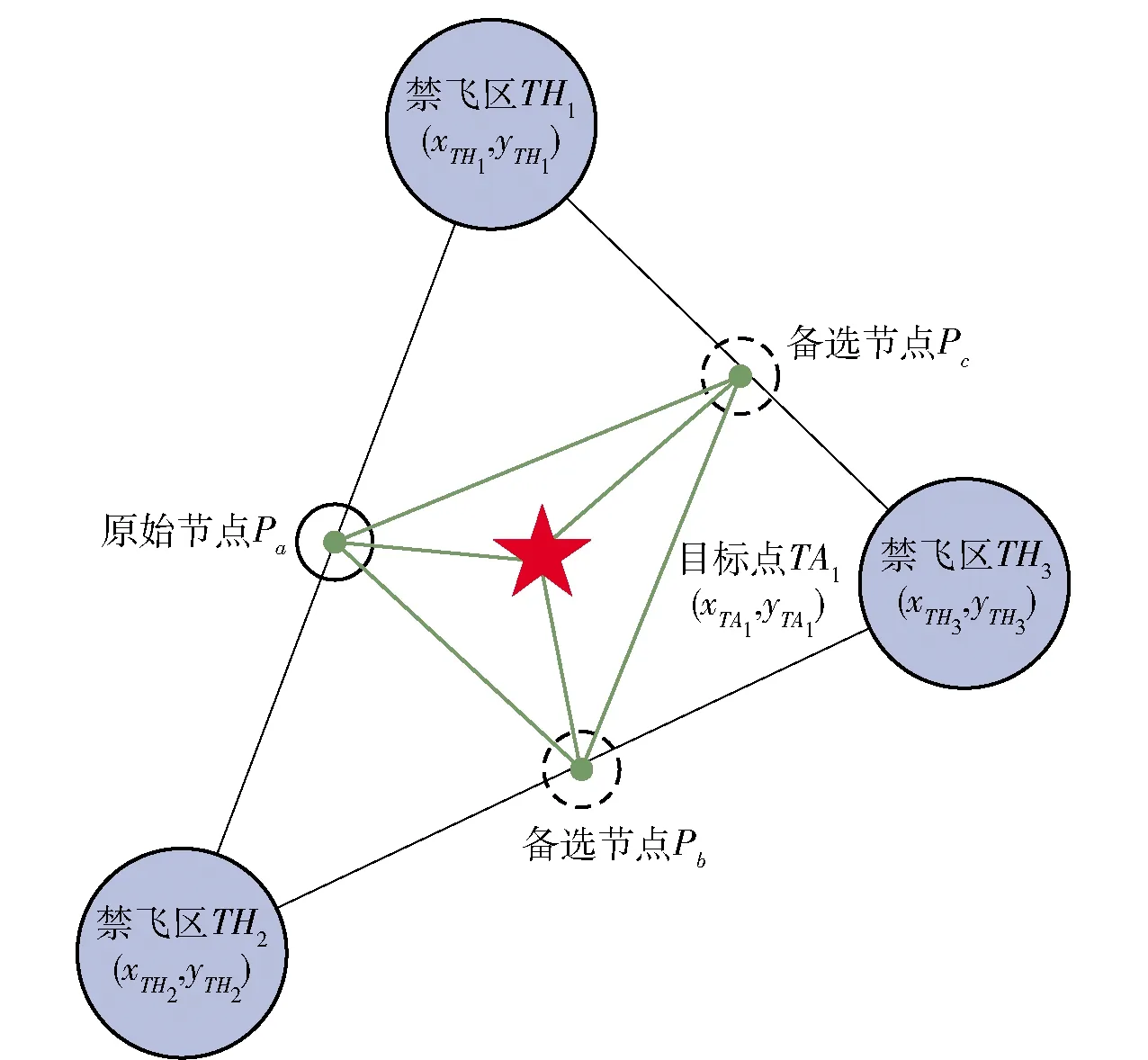
图9 目标节点搜索树
假设原路径中与终点连接的节点是Pa,这为重复攻击方向的无人机提供了额外的两个搜索节点{Pb,Pc}。根据搜索树建立方法,可以得出两个节点{Pb,Pc}距离最近的禁飞区有最大的安全距离,保障了节点的安全性。以{Pb,Pc}为终止目标点将原目标优化的代价函数f({Uk},{TAi},{THj})转化为对搜索节点P的代价函数:
(20)
式中:Pz∈{Pb,Pc}。通过优化搜索出到达节点Pb或Pc的最小化代价函数路径,从而实现对目标的多方向协同打击。
4 时间约束的协同轨迹优化及其跟踪
为了增加无人机突防成功率,且最大化打击效能,需要多架无人机能够时空同步打击多个目标。因此需要规划出满足时间约束的路径,且匹配设计路径跟踪控制器。
4.1 基于贝塞尔曲线的轨迹优化
为了满足时间约束和无人机自身的动力学约束,保证轨迹的连续平滑性,采用贝塞尔曲线对每架无人机的分段轨迹进行描述;通过对曲线的时间系数进行映射保证对目标的同时打击;为降低飞行过程中的能量损耗,设定Minimum Jerk为优化目标。
贝塞尔曲线由多个控制点定义,它总是过初始控制点和终止控制点,且曲线形状可以通过改变控制点改变。由于无人机可以解耦实现x轴、y轴两个方向的控制,因此可以独立地对x、y进行最优化处理。
贝塞尔曲线的表达式为
(21)
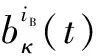
(22)
(23)
式中:μ为x轴、y轴任意轴上的B样条曲线;λ为B样条曲线分割段数;Sλ对应着每段路径的分配时间,即Sλ=Tλ-Tλ-1.
为了提升计算效率,每一段轨迹使用相对时间进行构造。以Minimum Jerk为目标函数,构建第k架无人机优化轨迹的数字表达形式为
(24)
式中:Tk表示第k架无人机的总时长。针对第ι段的分段贝塞尔曲线其表达式为
(25)
化简可得
(26)
式中:
(27)
相比于传统的多项式问题,基于贝塞尔曲线的Minimum Jerk目标函数表达式相对复杂,不利于构建形如J=pTQp二次函数形式,因此需要通过传统多项式进行求解。
此处建立传统多项式系数与贝塞尔曲线系数c的线性转换关系,将基于贝塞尔曲线Minimum Jerk的目标函数转化为J=cTMTQMc.针对8阶的贝塞尔曲线可以推导出
M=
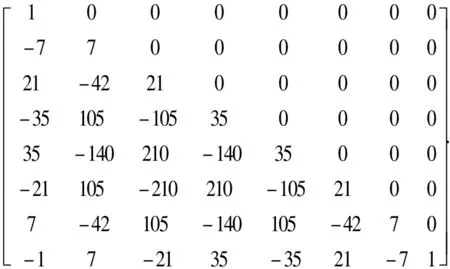
(28)
在此的基础上得到Minimum Jerk的时间归一化目标函数:
J=aTsTMTQMsa,
(29)
式中:a为归一化贝塞尔曲线控制点;s为每段对应的时间常数。
设定曲线Minimum Jerk问题的约束问题包括固定点约束、连续性约束和最大值约束。
固定点约束包括起点、终点的位置、速度、加速度约束,以及路径点的位置约束,通常的表达形式为
(30)
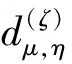
(31)
连续性约束则是每段路径的末位置和下一段路径初始位置之间的位置、速度、加速度约束,通常表示为
(32)
(32)式的位置点约束和连续性约束都为线性等式约束,可简化为Aeqc=beq,其中Aeq为等式关系中的参数矩阵,beq为等式关系中的参数向量,c=[c1,c2,…,cmc]。
为了保证轨迹的可行性,需要对无人机的最大速度和最大加速度进行约束。贝塞尔曲线具有凸包性质,只需要对每段曲线的控制点进行约束,即可实现对整条曲线的速度、加速度的约束,即
(33)
(33)式的速度和加速度约束则可以描述为线性不等式约束,即Aieqc≤bieq,其中Aieg为不等式关系中的参数矩阵,bieq为不等式关系中的参数向量,c=[c1,c2,…,cmc]。
那么轨迹生成问题可以重新写为
(34)
问题(32)式可以被转化为凸二次规划问题,可高效进行求解。
基于贝塞尔曲线,不仅可以实现无人机同时达到的要求,同时也满足位置、速度的光滑和加速度的连续约束条件,保证了飞行轨迹的可行性。
4.2 轨迹跟踪控制策略
在外界干扰和噪声条件下,为了使无人机能够精准跟踪预规划轨迹,需要设计轨迹跟踪控制器。
无人机路径规划可以得出每个时刻对应的无人机位置、速度、加速度控制量,据此通过姿态控制器实现轨迹跟踪,得到的轨迹控制回路如图10所示。
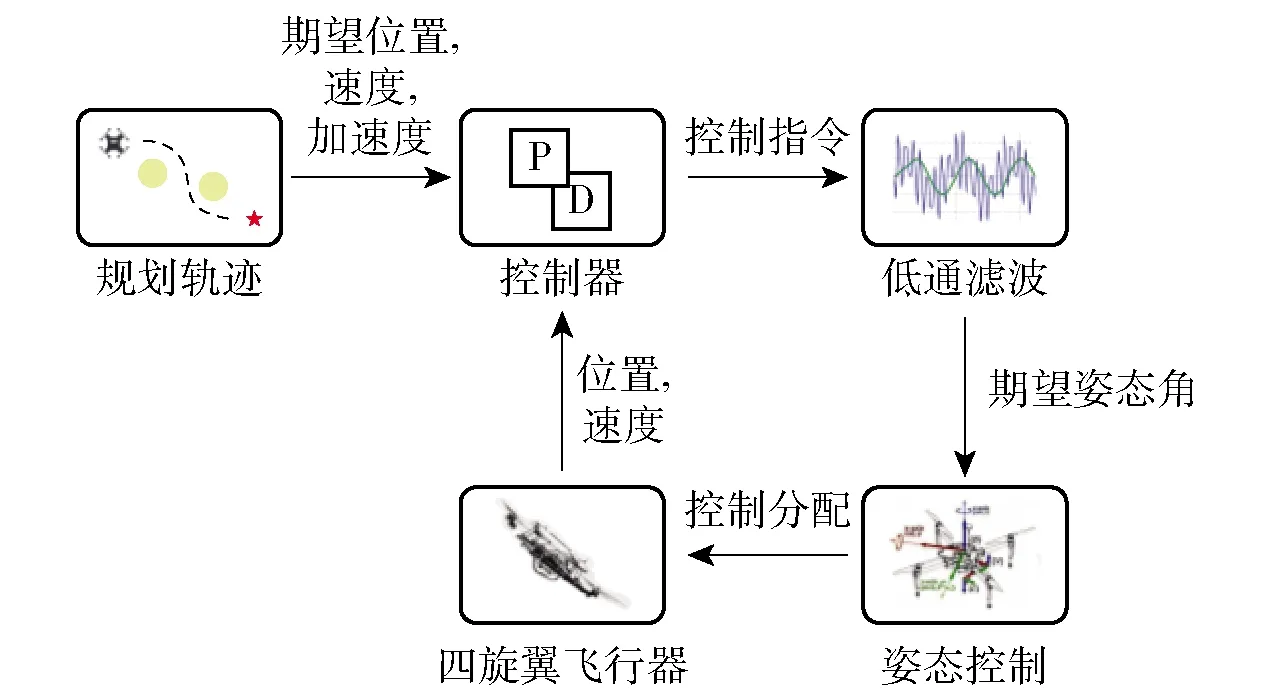
图10 无人机轨迹跟踪控制回路
为了无人机在传感器噪声和外界扰动条件下能够准确跟踪预定轨迹,计算出位置、速度、加速度误差作为PD控制器的输入量,并将输出结果作为无人机的闭环轨迹跟踪控制量,得到控制指令为
(35)
ac=pv·vd+pp·pd+
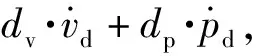
(36)
式中:vd、pd分别表示速度和位置的误差量;vs、vc分别表示设定速度和当前速度;ps、pc表示设定速度和当前速度;ac表示无人机加速度控制指令;pv、pp分别表示速度和位置的比例增益;dv、dp分别表示速度和位置的微分增益。
为了降低噪声等干扰因素对无人机控制指令的影响,在输入控制指令后添加低通滤波器为
(37)
式中:ac为经过低通滤波后的控制输入量;TL为低通滤波器时间常数;u为计算得到的控制输入量。
根据无人机动力学模型(35)式,可以将控制指令转化为对无人机姿态的实时控制量,即
(38)
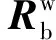
对(38)式进行整理,可以得到无人机加速度和姿态角之间的转换矩阵:
(39)
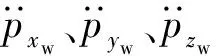
5 仿真分析
设定战场环境地图为10 km×10 km区域,其中存在5个无人机组成的攻击编队,3个攻击目标,以及若干禁飞区域,相关参数如表1所示。
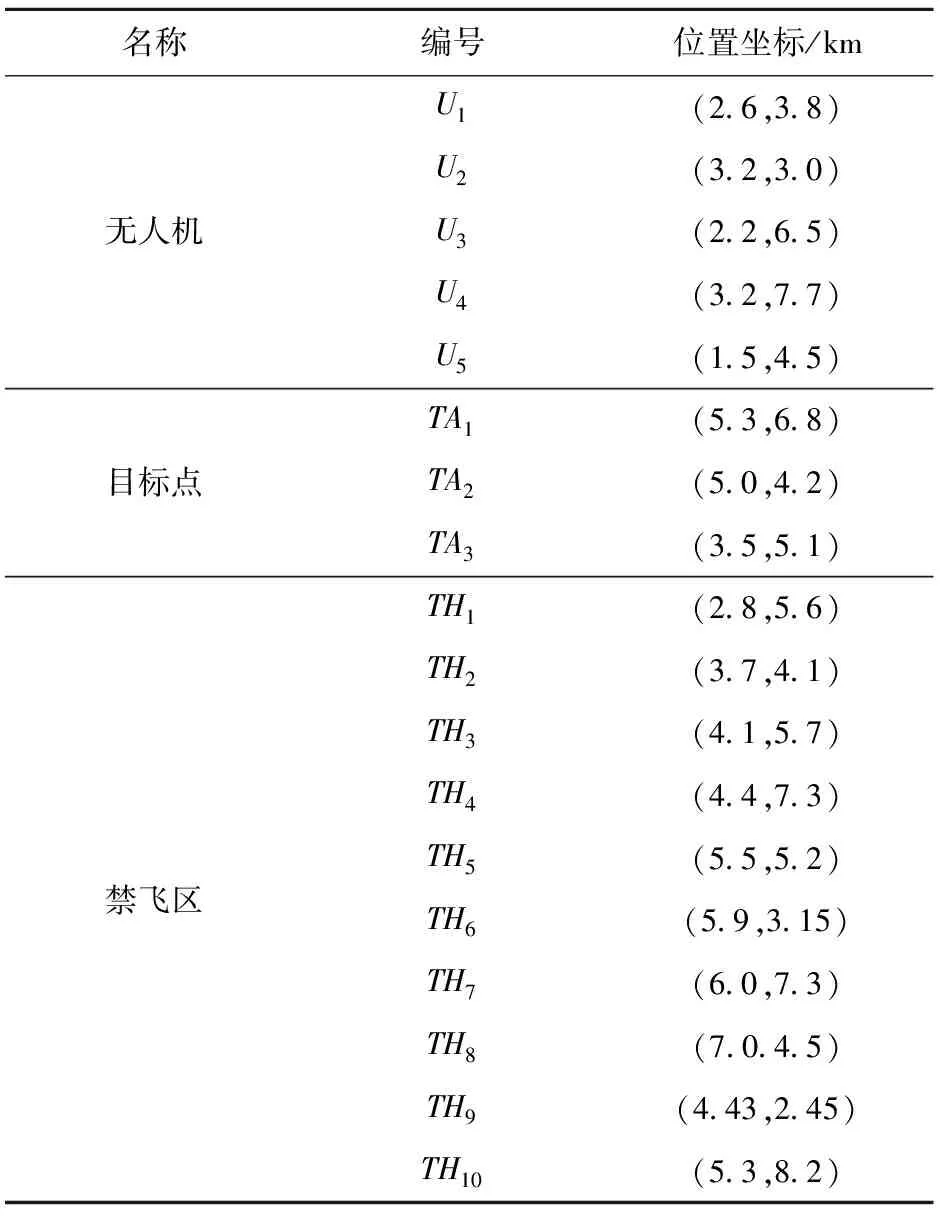
表1 仿真数据
5.1 任务分配与轨迹规划
5.1.1 任务分配与路径搜索
利用提出的Delaunay三角形划分方法,构建地图以及搜索树,结果如图11所示。
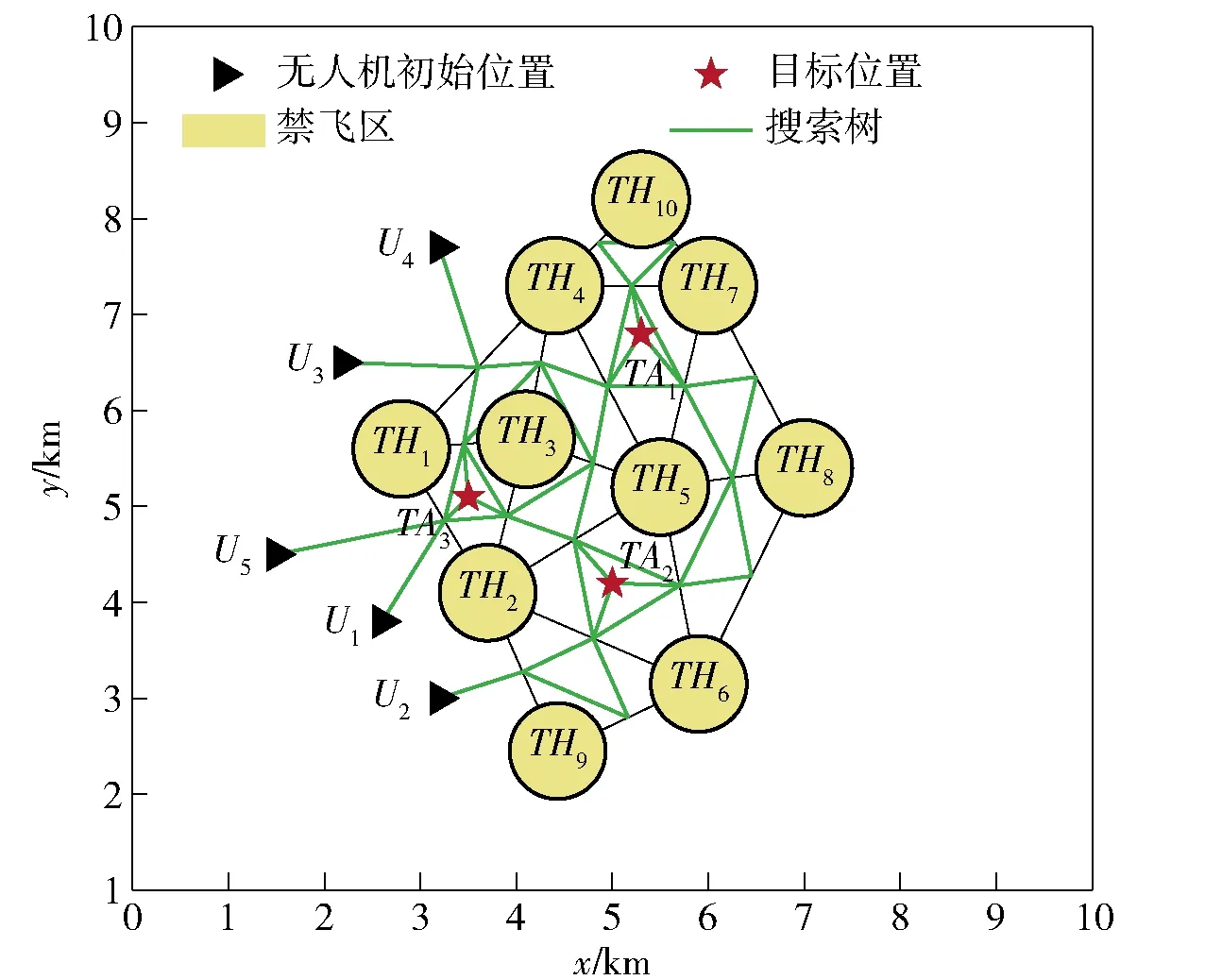
图11 多机Delaunay三角形地图构建
进而通过计算f({Uk},{TAi},{THj})函数,求出不同组合下的代价函数值,最终无人机按照任务分配矩阵[3,2,1,1,3]进行目标分配得到的代价函数值最小,得到无人机的多目标分配及其飞行路径如图12所示。
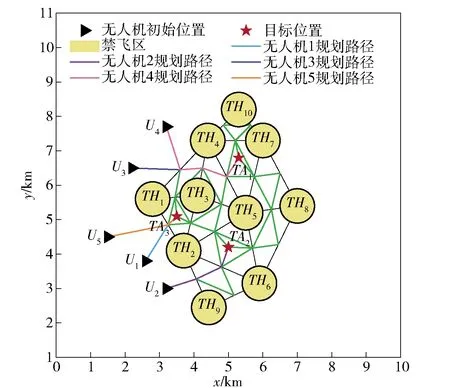
图12 多机任务分配结果
利用本文提出的多角度攻击分配算法,对具有相同攻击角度的无人机轨迹进行重新规划,可以得到不同终端攻击角度的无人机飞行路径,如图13所示。
由图13可知,在路径规划阶段实现了无人机的多目标打击任务分配、路径搜索以及单个目标的多方向打击。
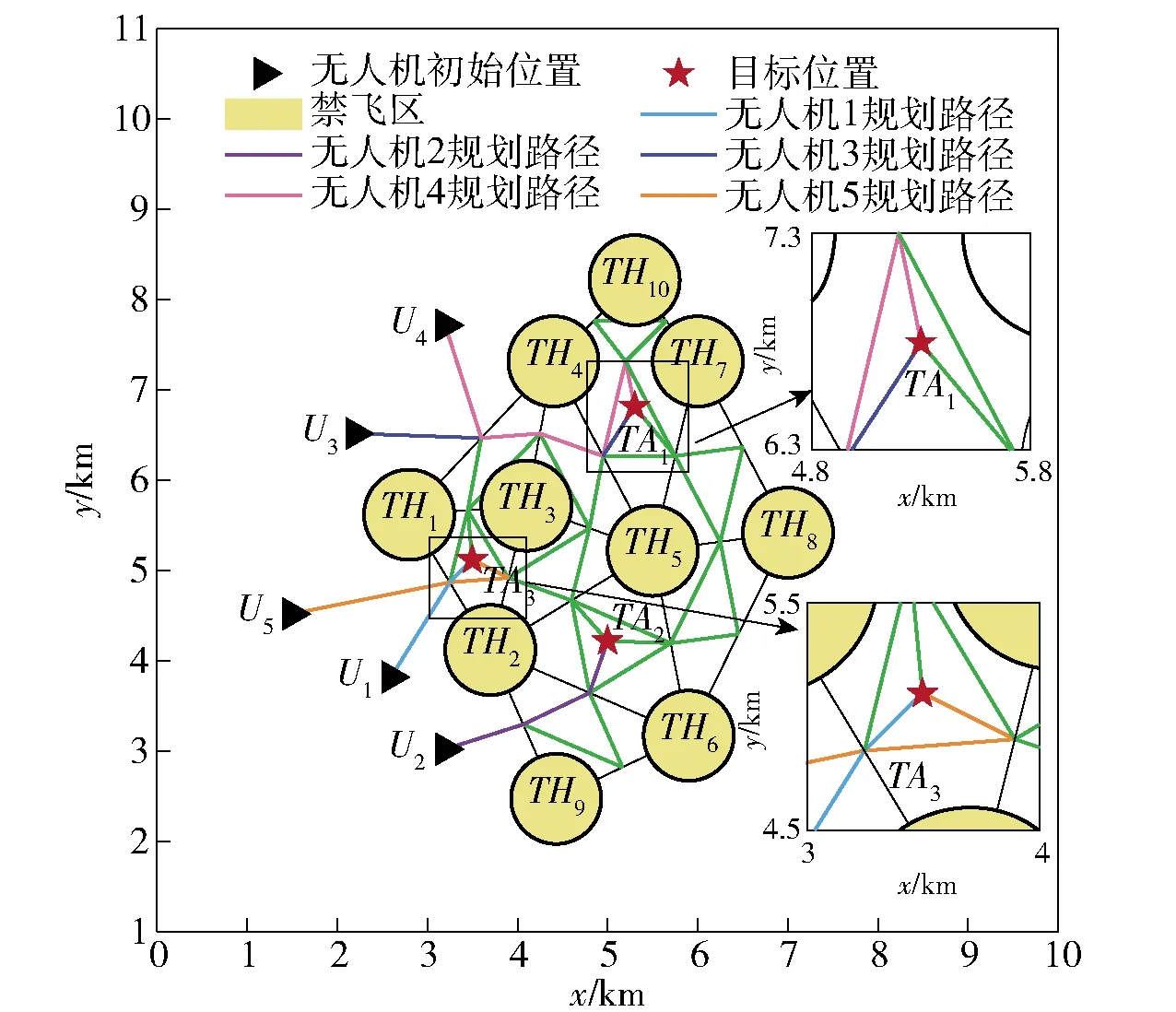
图13 多方位攻击任务设计
5.1.2 含有时间约束的轨迹优化
为在无人机动力学与时空同步到达约束下,保证问题可解,以最长路径的时间为总时长,进行各自无人机的时间优化。
选定规划总时间Ts=781 s,设定到达终点位置时的速度为4.5 m/s,x轴、y轴方向的速度约束分别为8 m/s,即最大飞行速度为11.3 m/s,x轴、y轴方向的加速度约束为2 m/s2.根据以上条件,对各无人机轨迹进行Minimum Jerk优化,得到5架无人机的飞行轨迹,如图14和图15示。
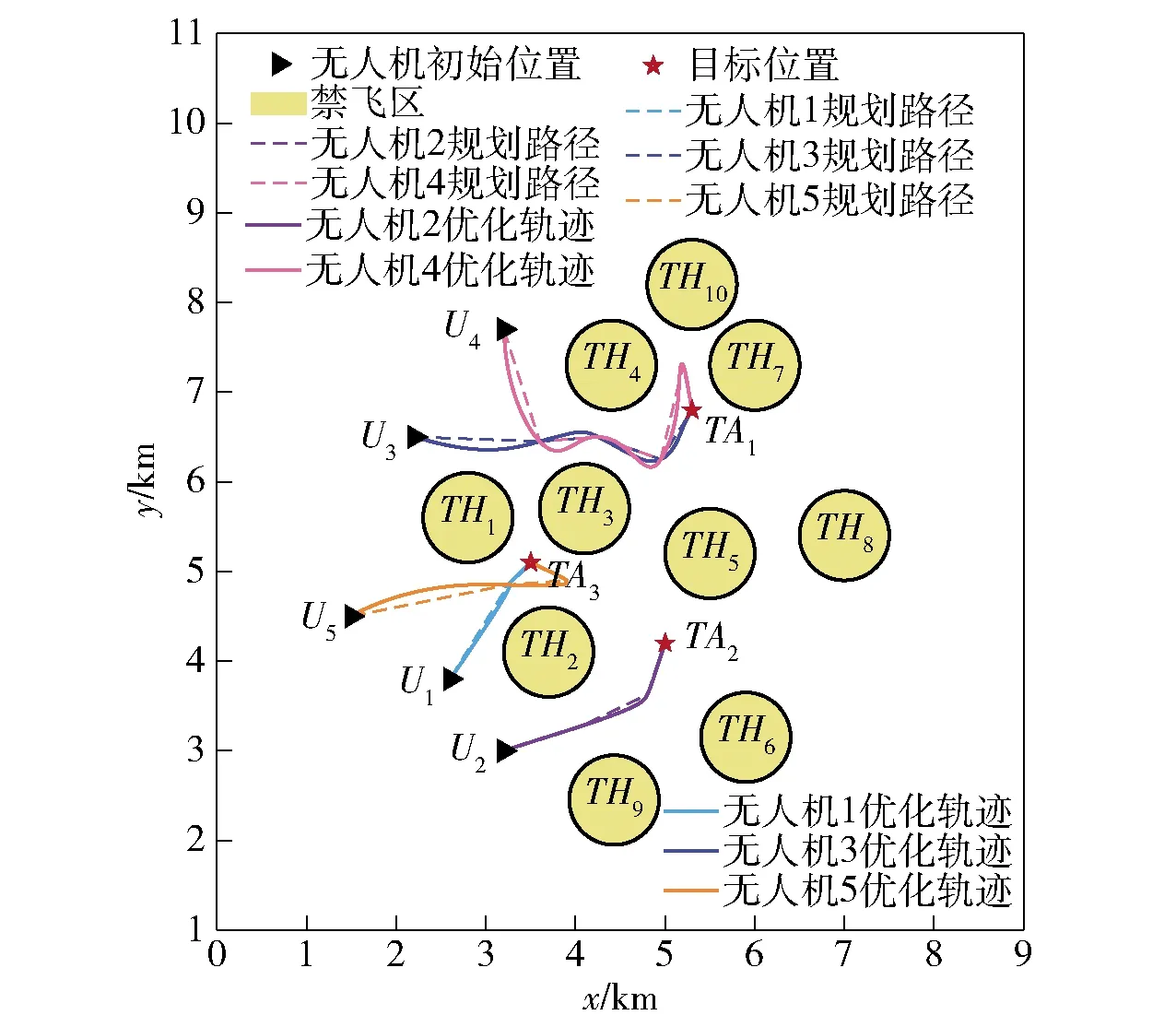
图14 贝塞尔曲线优化结果
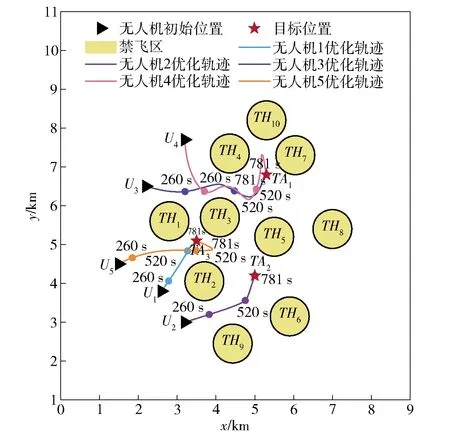
图15 贝塞尔曲线时序图
由图14和图15可知,利用本文提出的时间约束协同轨迹优化方法,规划得到5架无人机协同攻击轨迹,可实现从初始位置出发,经过路径规划的每个节点,并在第781 s同时到达目标位置。
图16分别给出了5架无人机x轴、y轴方向的速度和加速度曲线。由图16可知,规划得到的无人机位置和速度均为平滑曲线,且加速度曲线连续,并且速度和加速度均满足无人机约束条件。
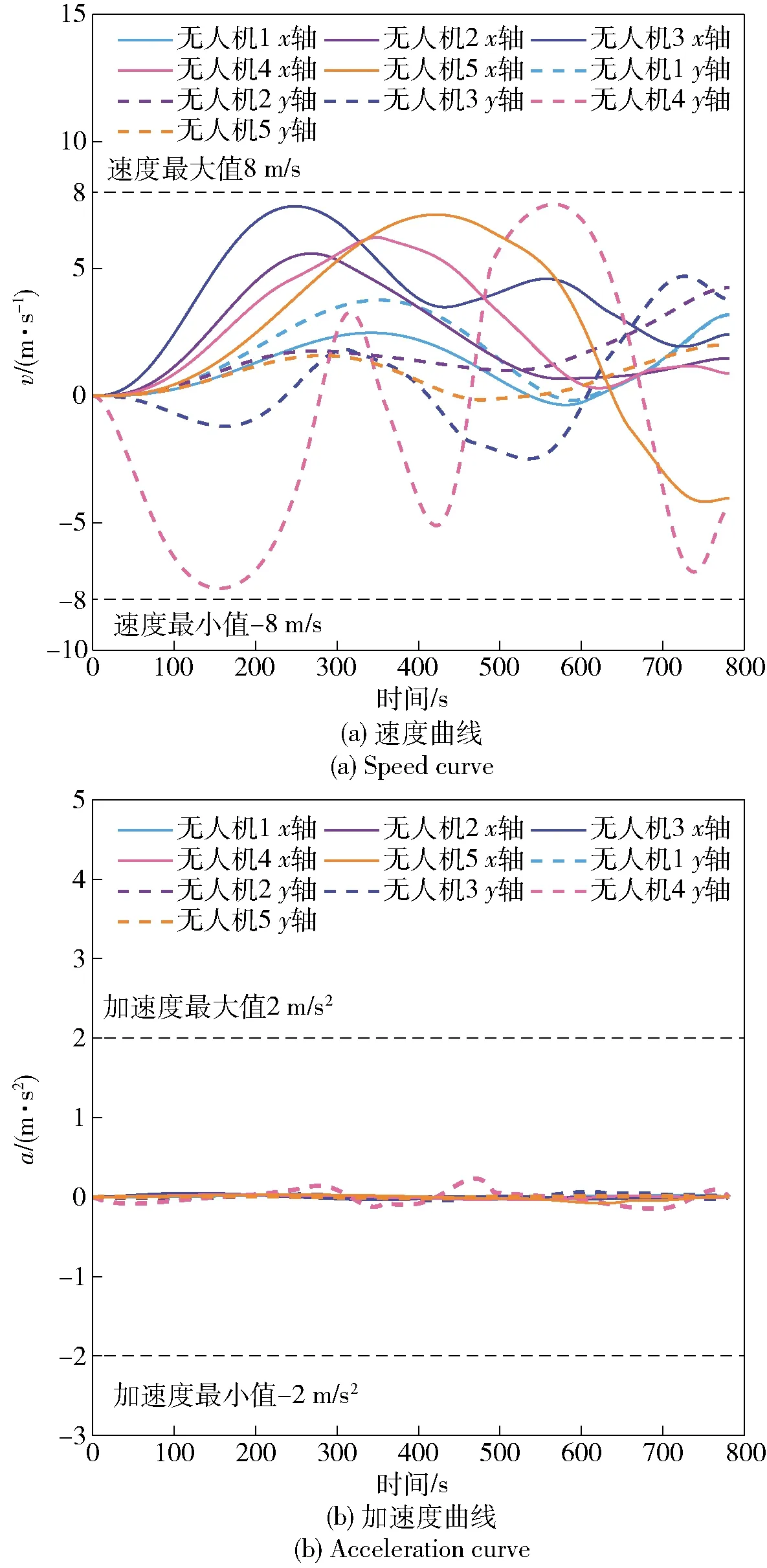
图16 无人机速度和加速度曲线
5.2 协同轨迹跟踪
为了比较分析无人机规划轨迹在有无噪声和干扰条件下的跟踪特性,采用辨识得到的实际某型无人机姿态动力学模型:
(40)
式中:φd、θd、ψd为期望输出角度;φ、θ、ψ为实际输出角度。
5.2.1 理想情况
理想情况下不考虑传感器噪声和干扰,分别设计速度控制、位置控制的比例增益系数pv=2.5、pp=0.001.速度控制、位置控制的微分增益系数dv=1、dp=0.001.利用数学分析软件MATLAB/Simulink进行仿真,设定脱靶量1 m为终止条件,统计各个无人机的到达时间,仿真结果如图17所示。
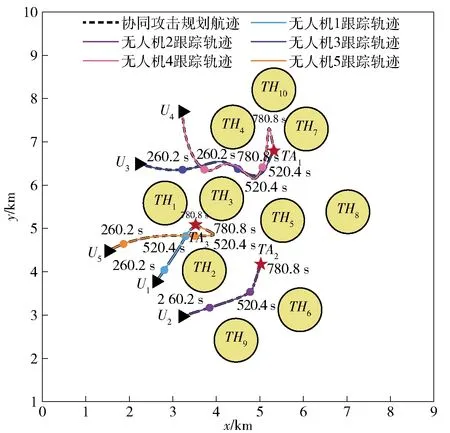
图17 理想条件下多无人机协同轨迹跟踪
由图17可知,5架无人机均能够准确跟踪预规划飞行轨迹,且5架无人机同时到达各自目标位置,构成分布式协同攻击。
5架无人机的速度和加速度曲线如图18和图19所示。由图18和图19可知,轨迹跟踪控制器不但能够控制5架无人机准确跟踪轨迹,还能够稳定跟踪速度曲线,且无人机速度和加速度均满足设定的约束条件。
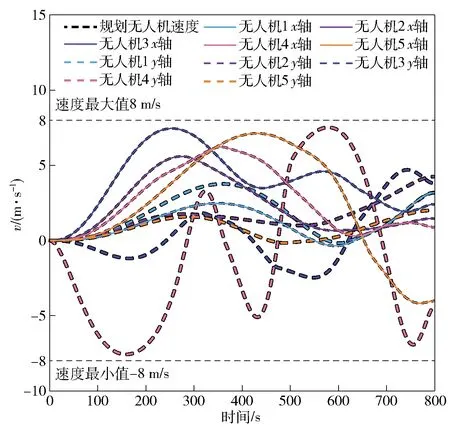
图18 理想条件下多无人机速度曲线
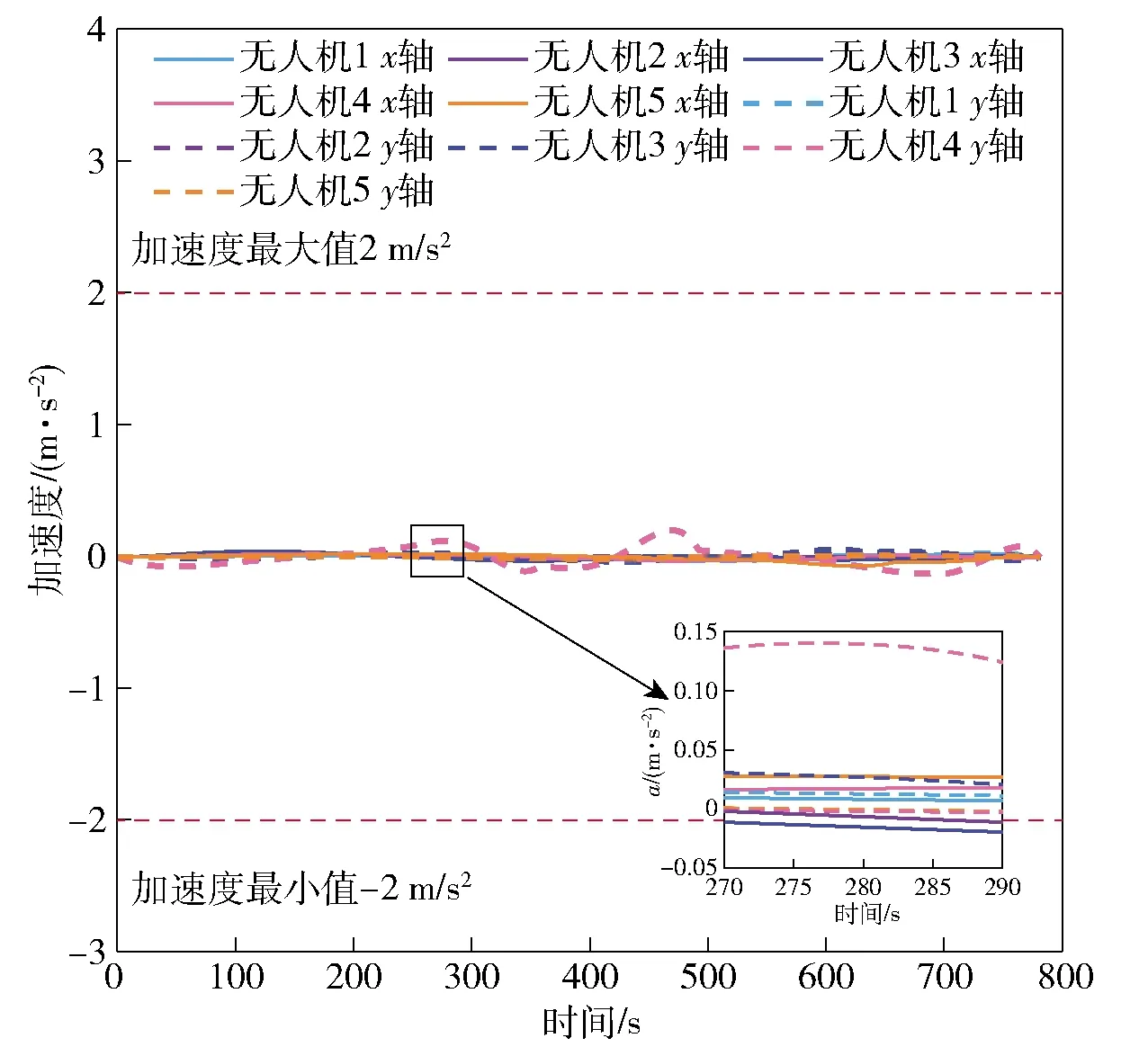
图19 理想条件下多无人机加速度控制指令
5.2.2 引入噪声及阵风干扰
与此同时,环境中还存在风的干扰,此处考虑阵风干扰。参考文献[26],阵风干扰模型可描述为
(41)
式中:vg为干扰的风速;vmax为最大风速;t1表示开始受风影响的时间;Tg表示风持续影响的时间。
根据动量定理,推导出风对无人机的干扰力,即
(42)
式中:ρ为空气密度,取ρ=1.205 kg/m3;S为无人机阵风受力面积。假设无人机在仿真过程中400 s时,受到沿y=x直线方向的6级阵风干扰(11 m/s),持续时间为5 s.
为了降低噪声和阵风干扰对控制指令的影响,设定低通滤波器参数TL=1,仿真结果如图20所示。由图20可知,即使引入噪声及阵风干扰,5架无人机的轨迹跟踪控制器依然可以准确控制无人机跟踪预先规划轨迹,实现从不同初始位置对多个目标的时空同步攻击,达成分布式协同攻击效果。5架无人机的速度和加速度曲线如图21和图22所示。
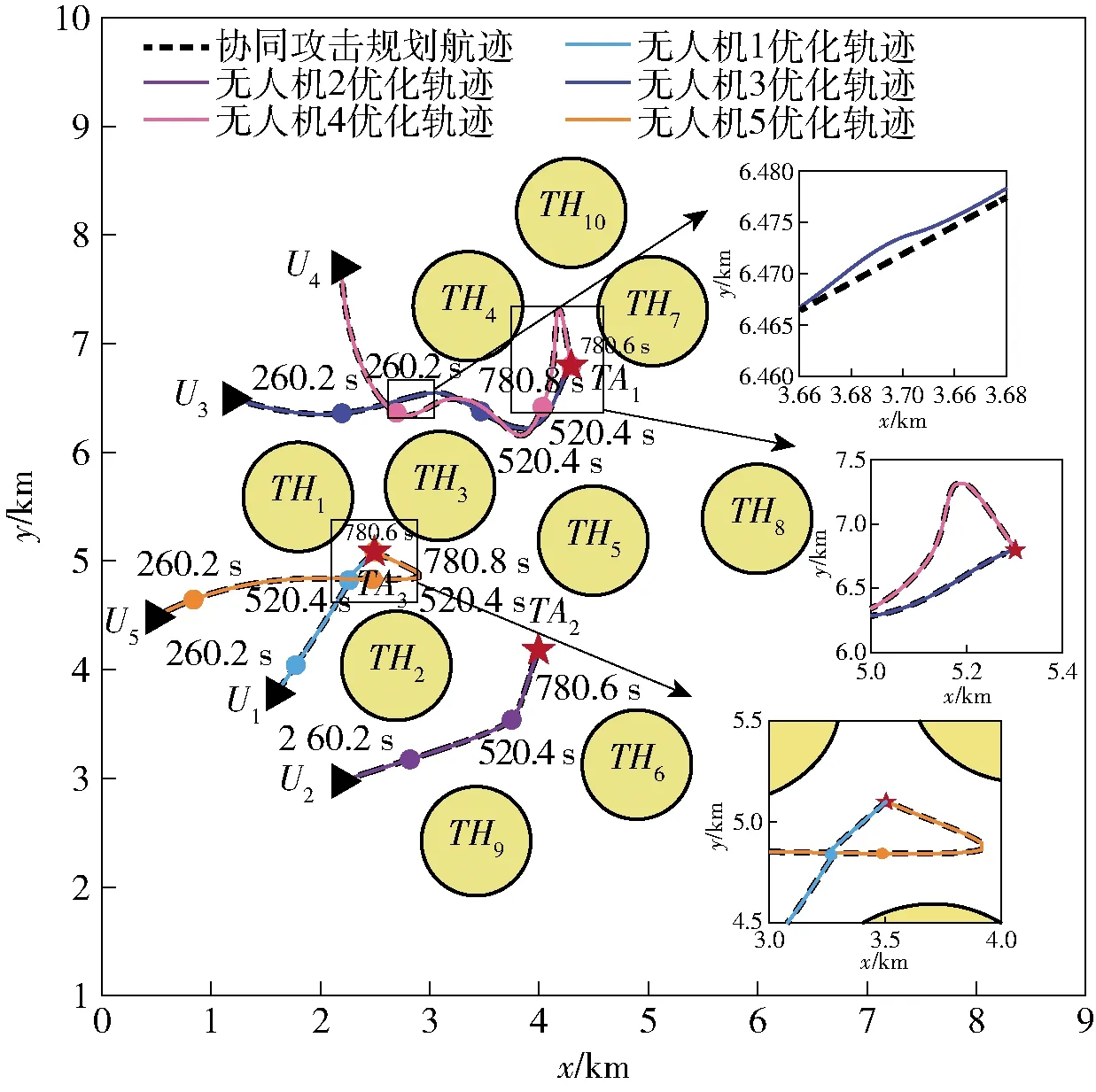
图20 噪声及干扰下多无人机协同轨迹跟踪
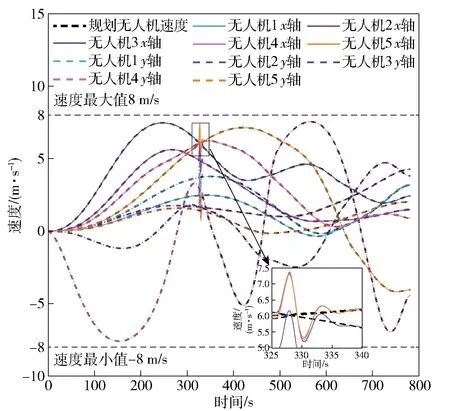
图21 噪声及干扰情况下多无人机速度曲线
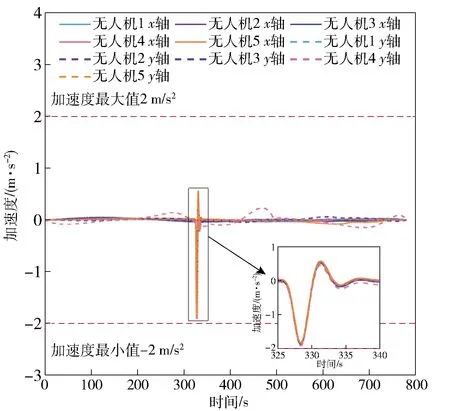
图22 滤波后多无人机加速度控制指令
由图21和图22可知,在噪声及阵风干扰下,5架无人机速度和加速度均满足约束条件要求,且无人机的轨迹跟踪控制可以很好地抵抗阵风干扰,具有一定的鲁棒性。
在此基础上,统计2 000次引入测量噪声和阵风干扰情况的无人机协同攻击效果如表2所示。
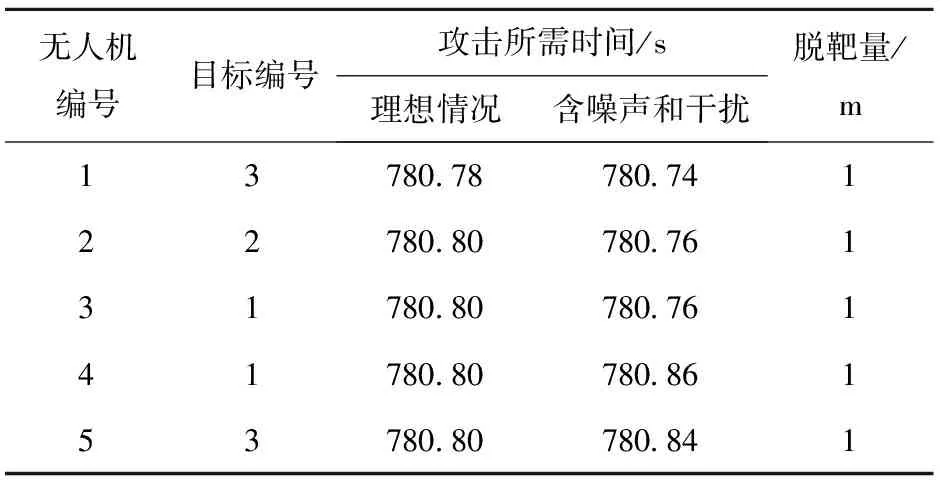
表2 理想情况、引入噪声及阵风干扰协同攻击效果比较
由表2可知,考虑噪声及干扰条件下,5架无人机之间的协同攻击时间误差均小于1 s,表明本文的多无人机协同攻击策略对干扰具有较好的鲁棒性,满足复杂战场环境下多目标时空同步攻击要求。更为重要的是,本文提出的时空同步协同攻击策略不依赖于无人机间的组网通讯,极大地增加了可靠性,具有较强的工程实用性。
6 结论
本文针对复杂战场环境下多目标分布式时空同步协同攻击问题,提出一种多目标任务分配与时间约束的协同路径规划算法,兼顾了无人机目标分配的最优性与规划效率,可实现多目标的时空同步协同打击,提升无人机的突防概率和打击效能。得出主要结论如下:
1)利用Delaunay三角形的空外接圆和最大最小角性质,将地图划分成最小单元,构建战场态势地图,可提高无人机飞行过程中规避禁飞区的安全性。
2)提出基于sigmoid函数对任务分配结果进行评估,可提升多目标分配问题的优化求解效率,保证无人机任务平均分配的同时尽可能地提升对重要目标的打击力度。
3)基于贝塞尔曲线对设计的路径施加位置和动力学约束,使得控制指令连续平滑,保证飞行路径满足约束条件。且通过引入时间调节因子,实现了对多目标的同时到达攻击。
4)仿真结果表明,本文多目标分配与轨迹规划方法可兼顾效率与最优,在噪声及阵风干扰下,亦能有效地保证分布式协同攻击的时间一致性。且无人机间的协同不依赖于通信网络,具备通信拒止环境下的协同攻击能力,具有较高的实际应用价值。
