侧扫声纳图像非下采样轮廓波变换域分区增强方法

武鹤龙，邱政，张维全

(91388部队, 广东 湛江 524002)

0 引言

近年来，侧扫声纳在海洋开发和利用以及军事应用方面发挥着日益重要的作用，广泛应用于水下工程勘察、水下物体打捞、海底地质探测、水中目标探测、海上导航等领域。然而因为复杂多变的海洋环境以及声传播的多途效应，造成与光学和雷达图像相比，侧扫声纳图像具有其独特的性质。声波强度在传播过程中的快速衰减、海水温度与盐度的分布不均导致的声速不规则变化、严重的海洋噪声以及声纳设备自噪声等导致侧扫声纳图像包含斑点噪声、条带噪声、目标边缘模糊、辐射畸变、几何畸变等降质现象[1]，给侧扫声纳图像的目标判读造成了一定的困难，所以在对侧扫声纳图像进行目标检测前，需要进行预处理，以消除噪声、提高图像对比度以及对感兴趣区域进行增强。

传统的小波变换方法在信号以及图像去噪及增强中表现出良好的性能，然而小波基不具备各向异性的条件，其在表征点状奇异性的优势并不能应用于表征图像中的线状奇异性，如纹理、边缘等，各种能够稀疏表示图像线特征的超小波应运而生[2]。作为超小波的一种，非下采样轮廓波变换(NSCT)具备诸多良好的性质，如实现了对线状奇异性最好的稀疏表示、具备各项异性可以对图像进行不同方向的分解、具有平移不变性可以消除伪吉布斯现象等[3]，因此NSCT在图像处理的许多领域得到广泛应用。

本文基于对NSCT域系数的统计特性分析，提出一种对侧扫声纳图像进行分区增强的方法。实验证明，该方法不仅消除了大部分斑点噪声，抑制了琐碎的纹理，而且较好地提升了图像低频区域灰度对比度以及增强了高频区域的边缘细节部分。

1 非下采样轮廓波变换

NSCT为多尺度几何分析的一种，不同的多尺度基函数可对不同特征的信息进行稀疏表达。NSCT具有一定的方向分辨率，具备各项异性的特征，能克服小波变换缺乏方向信息表达的缺点，更高效地表示图像中边缘轮廓纹理等具有方向性的特征[4]。

NSCT将拉普拉斯塔形分解(LP)和非下采样方向滤波器组(NSDFB)相结合，从而实现对图像的多分辨表示。NSCT基的支撑区间具有随尺度变化长宽比的长条形结构，具有方向性和各向异性[5]。在NSCT分解系数中，表示图像纹理、边缘的系数能量更加集中，或者说NSCT变换对于线性奇异性结构具有更稀疏的表达。NSCT将多尺度分析和方向分析分拆进行，首先由LP变换对图像进行多尺度分解以捕获点奇异，接着由NSDFB将分布在同方向上的奇异点合成为一个系数。在NSCT的分解重构过程中，没有按照传统Contourlet的方法对图像进行上采样和下采样，这样分解后的子带图像和原图像大小保持一致，具有了Contourlet变换不具备的平移不变性[6]。而二维小波是由一维小波张量积构建得到，它的基缺乏方向性，不具有各向异性,不能够对线性奇异性结构进行稀疏性表达。NSCT过程如图1所示。

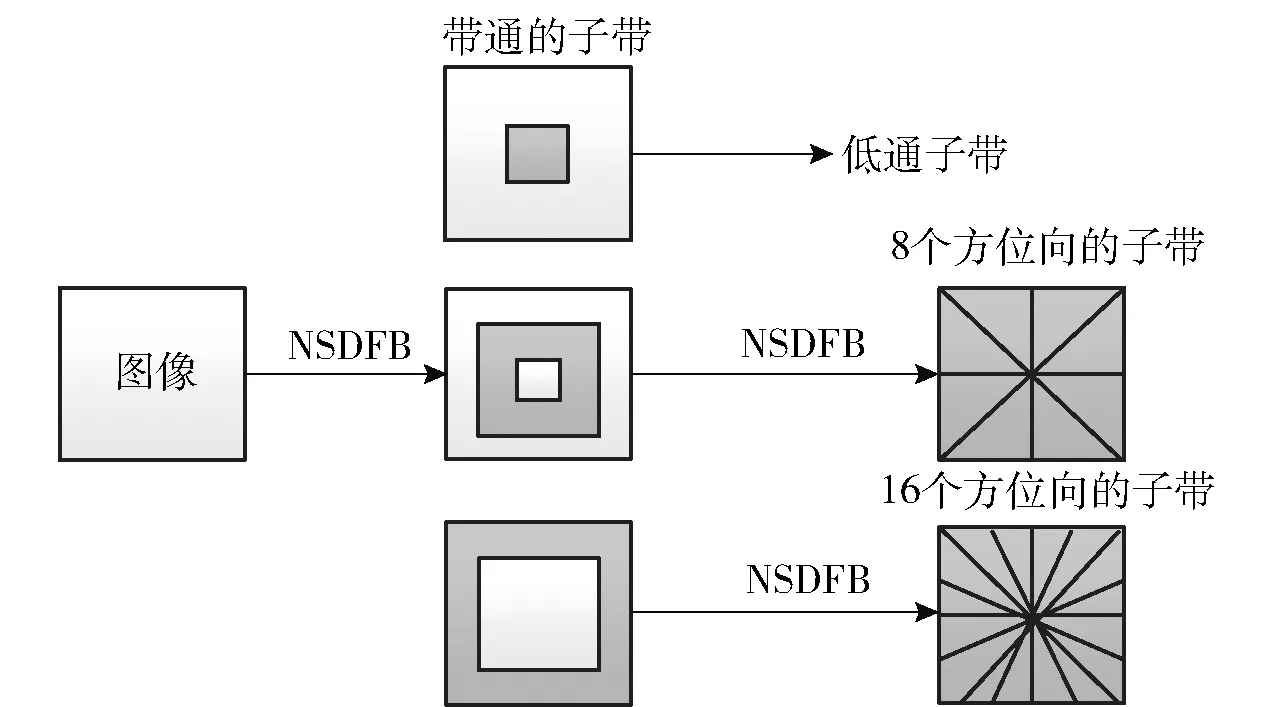
图1 NSCT过程

2 NSCT域分区增强方法

NSCT域分区增强方法实现步骤为：首先，对于声波衰减严重造成的远距离和近距离图像之间的灰度反差，由于其分布在图像的低频区域，所以在低频区域先进行灰度均衡，而后非线性拉伸，消除灰度分布不均，提升对比度；其次，对于分布在高频区域的斑点噪声、纹理、弱边缘以及强边缘，采用NSCT域分区方法进行区域划分，而后将噪声区域系数置0，消除噪声，对纹理、弱边缘、强边缘区域的系数，采用分段函数处理，实现不同程度的抑制和提升；最后，对增强后的低频区及高频区进行NSCT反变换重构，获得最终的侧扫声纳增强图像。

2.1 低频尺度对比度增强算法

声纳图像经过二维小波变换和各种超小波变换后，低频尺度主要为图像灰度的缓慢变化部分，反映了声纳图像的概貌以及由声纳系统成像机理造成的灰度不均。声纳成像的质量欠佳，灰度对比度低，需要在预处理步骤中进行增强。本文对侧扫声纳图像低频部分进行非线性拉伸，提升灰度对比度，即达到将暗区域显示更暗、亮区域显示更亮的效果。具体方法为先将低频系数归一化，而后根据非线性增强函数，对归一化低频系数进行增强，提升低频图像对比度。

本文采用的非线性增强函数为

(1)

式中：x为增强前灰度值；y为增强后灰度值；参数r控制函数的斜率；参数a影响斜率变化的位置。图2为非线性增强函数的示意图。

图2 非线性增强函数

若斜率r过高会造成灰度对比度过度提升，造成明暗区域过度增强，视觉效果较差；若斜率r过低，则灰度对比度提升不足，增强效果较弱。因此本文r选取为经过测试和综合考虑而选择的适中值。本文选择a=0.5、r=4.

选取3幅侧扫声纳图像，对图像的低频尺度按照增强函数进行处理，结果如表1所示。

表1 低频尺度原图像以及增强后的图像

在上述低频尺度增强结果中，各低频尺度图像上的暗区域经过处理后暗的程度得到加强，而亮的区域则呈现得更加明亮，灰度对比度得到很大的提升，目标区域获得凸显。

2.2 侧扫声纳图像NSCT域高频尺度区域划分及增强算法

声纳图像的高频尺度包括噪声、纹理以及边缘部分，高频尺度的增强原则为在较好地抑制噪声前提下增加纹理、边缘的强度，需要先对噪声以及纹理、边缘进行有效的划分，然后根据不同区域内图像分量的类型分别进行对应处理。

2.2.1 侧扫声纳图像高频尺度区域划分

相较于斑点噪声，纹理以及边缘具有线状奇异性以及方向性，表现在NSCT域中：若沿纹理以及边缘方向的正交方向进行分解，则系数最大；若沿纹理和边缘所在的方向进行分解，则系数最小，并且如分解方向与纹理、边缘所在方向的夹角越小，则分解系数越小[7]，即在同一尺度内不同的方向子带上，纹理、边缘的系数大小存在不同程度的差别。对于噪声，由于其不具备方向性，沿不同的方向进行NSCT分解，其系数大小近似，差别较小。

进一步分析可以得出，强边缘在同一尺度内不同方向子带上的最大系数与最小系数的差值最大，弱边缘系数的差值稍小于强边缘，纹理区域次之，而噪声各个方向子带最大系数与最小系数的差值最小。

NSCT能够对线状奇异性进行很好的稀疏性表达，在NSCT域，具备线状奇异性特征的纹理、边缘被分解为稀疏的较大系数，而分布数量众多的数值较小系数则表示不具备方向性和线状奇异性的斑点噪声。推导可知，纹理、边缘在同一尺度内不同方向子带上最大系数与最小系数的差值也具备稀疏性，而噪声在各个方向子带上最大系数与最小系数的差值不具备稀疏性。对声纳图像NSCT域同一尺度内不同方向子带上的最大系数与最小系数的差值矩阵做直方图统计，纹理、边缘在系数差值矩阵统计直方图上的数值比较大，分布较为分散，噪声的数值比较小，分布较为集中。

选表1中侧扫声纳图像示例1，对其进行多尺度多方向NSCT分解，设置拉普拉斯金字塔分解的尺度数为4，拉普拉斯金字塔分解高频尺度上的方向分解参数依次设为4、4、4，即低频尺度(最粗尺度)方向数默认为1，高频第2、第3、第4尺度进行24=16个方向的分解。经过上述参数设置的NSCT分解后，示例1图像分解为一个无方向的低频子带以及第2、第3、第4尺度各16个方向的高频子带。在第2高频尺度上，计算各像素点对应16个方向子带的最大系数与最小系数差值，获得差值矩阵，而后对差值矩阵做统计直方图，如图3所示。由图3可知，声纳图像各像素点所对应的方向子带系数最大系数与最小系数差值分布呈现为中间峰值凸起、两边逐渐下降，并且右边差值较大区域的梯度下降比较平缓，呈长拖尾形状，而左边差值较小区域的梯度下降较大，坡度陡峭。这说明中间的峰值区域差值系数分布最集中，两边分布较为稀疏，并且峰值的右侧区域差值系数分布稀疏度更大。

图3 方向子带最大系数与最小系数差值矩阵统计直方图

根据噪声方向子带系数差值比较小，并且分布不具备稀疏性的特点，可知从最左侧接近0的位置到分布最为集中的峰值区域主要表示斑点噪声，而由于纹理、边缘的最大系数与最小系数差值比较大，并且分布稀疏，所以在图3上，它们分布在峰值右边的区域。选取直方图峰值处所对应的系数差值作为区分噪声的阈值，当某像素点所对应的方向子带最大系数与最小系数差值小于该阈值时，判断其为噪声，否则为纹理或者边缘。

假设峰值处所对应的横坐标为z1即区分噪声和纹理边缘的阈值。直方图上存在系数分布的横坐标最大数值为zm.从峰值处横坐标往右沿差值系数增大的方向直至最大数值zm位置，此区间段统计分布包含了纹理、弱边缘以及强边缘3种形态分量，因为纹理、软边缘、强边缘的NSCT域同一尺度的最大和最小方向子带系数差值依次增大，并且稀疏度也逐渐变大，所以可以推断纹理、弱边缘、强边缘在峰值右侧区域按照差值系数由小到大的次序分布。示例1图像差值系数统计直方图区域划分如图4所示。

根据侧扫声纳图像上纹理、弱边缘、强边缘常规的数量分布以及实验效果评估情况，本文将直方图峰值处到最右侧系数分布区域处的横坐标从左到右依次划分为纹理、弱边缘、强边缘3个区间，纹理占横坐标左侧1/5对应的区域，弱边缘占中间2/5的区域，强边缘占右侧2/5的区域。划分定义式为

(2)

式中：z为各像素点各方向子带最大系数与最小系数差值。

2.2.2 NSCT域高频尺度分区增强算法

在NSCT域高频尺度区域划分之后，就可以针对不同区域的系数进行相应的处理以达到图像增强的目的。

本文对各区域系数的处理策略为：对于噪声区域的系数，直接置为0，消除噪声；对纹理区域系数进行0.5倍的灰度范围压缩，抑制纹理；弱边缘区域进行2倍的灰度范围扩展以提升对比度，并且将范围扩展后的系数增加一个固定值以增加亮度；强边缘区域系数保持不变。这就实现了在消除噪声的同时抑制纹理以及增强弱边缘的目的。

采用分段线性增强函数，如(3)式所示：

(3)

计算各个区域的系数经过不同的线性单值函数处理后的结果，而后将NSCT域低频系数置0，对增强后的高频系数进行NSCT反变换，即可得到高频尺度增强图像。

2.2.3 高频尺度增强结果与分析

选取3幅侧扫声纳图像，其高频尺度增强后的结果如表2所示。从第1幅示例图像的高频尺度增强结果可以看出，绝大部分背景噪声被消除，弱边缘稍微凸显，在第2、第3幅示例图像的结果中边缘增强效果体现的更明显，噪声基本消除，一些琐碎的纹理得到抑制，弱边缘获得一定程度的增强。

表2 高频尺度增强结果

3 实验结果与分析

将增强后的低频系数、高频系数分别进行NSCT反变换重构，就可以得到侧扫声纳图像最终的增强结果。

目前还没有统一的对侧扫声纳图像增强效果的客观评价指标。本文以对感兴趣区域诸如低频部分、高频边缘部分灰度对比度增强的视觉效果以及平滑指数FI、边缘保持指数EPI作为评价标准[8]。FI用以评估增强方法对图像斑点噪声的抑制能力，FI值越大，抑噪平滑能力越强[9]。EPI表示对图像边缘细节信息的保持及增强能力EPI值越大，边缘保持及增强能力越强[10]。

将本文方法与小波硬阈值增强方法、小波Shrinkage自适应阈值增强方法做比较。其中小波硬阈值增强方法为将分解后的低频系数中大于低频阈值的系数放大至1.5倍，而高频细节部分小于高频阈值的系数弱化为原来的0.75倍，而后进行系数重构，阈值采用蒙特卡洛方法计算获取[11]。小波Shrinkage自适应阈值增强方法为计算小波系数邻域的局部方差数值，将其与估计的噪声方差做比较，小于噪声方差的系数置0，其余的系数进行1.2倍的放大，从而进行噪声消除和图像增强[12]，选取局部窗口大小为3×3.3种增强方法的对比结果如表3所示。

表3 3种方法增强结果

比较上述3种增强方法的结果图像，分析可知小波硬阈值增强方法在整体视觉效果上增加了一定程度的对比度，但是受阈值选取的准确度影响，其没有很好的将噪声与纹理、边缘进行有效的区分，所以对系数的处理造成噪声消除效果不佳以及边缘模糊。采用的小波Shrinkage自适应阈值增强方法在消除部分斑点噪声的同时，较好地保留了边缘信息，对比度也有所提高，视觉效果好于小波硬阈值增强方法，但噪声消除的效果不及本文方法。在本文方法增强的3幅示例图像中，噪声基本消除，部分琐碎的纹理被抑制，一些弱边缘得到增强，加上低频尺度的增强效果，使得感兴趣目标的对比度获得很大提升。在示例3的增强结果中高频尺度分区域增强的作用体现得比较明显，可以清晰地看到噪声消除、纹理抑制以及弱边缘增强的效果。

对3种方法的去噪效果做定量评估。选择本文方法的噪声抑制部分，不进行边缘的增强处理。将本方法的噪声抑制效果与小波硬阈值去噪方法、小波Shrinkage自适应阈值去噪方法做比较。遥感图像抑噪质量评价的准则是抑噪方法能够在较好地保持图像边缘纹理细节信息的前提下，较大程度地抑制斑点噪声。抑噪效果的评价标准主要包括平滑指数FI以及边缘保持指数EPI.

一种好的抑噪方法首先要能较好地保持图像边缘纹理细节，即不对SAR图像中有用信息造成过多损失，而后在此前提下尽可能多地抑制斑点噪声，这样使得保持边缘细节和抑制斑点噪声二者达到一种适度的平衡[13]。本文随机选取31幅侧扫声纳图像，分别按照上述3种方法进行去噪，计算各方法去噪指标并分析去噪效果。3种方法对示例侧扫声纳图像去噪的平滑指数及边缘保持指数对比如图5及图6所示。

由图5、图6可知，各方法对示例图像的平滑指数均值接近，说明本文方法和其他两种方法抑制斑点噪声的性能类似。本文方法边缘保持指数平均值高于小波硬阈值以及小波Shrinkage自适应阈值增强方法，说明本文方法在抑制噪声的同时可以较好地保留边缘细节信息，体现出在边缘保持及提升目标对比度方面的优势。

图5 3种增强方法的平滑指数对比

图6 3种增强方法的边缘保持指数对比

4 结论

在低频尺度本文对侧扫声纳图像使用分线性增强函数扩展灰度范围，提升灰度对比度。在高频尺度利用各像素点NSCT域方向子带系数最大系数与最小值的差值矩阵统计规律，结合NSCT对线性奇异性的稀疏表示，将其划分为噪声、纹理、弱边缘以及强边缘区域，采取线性分段函数处理各区域系数，以达到消除噪声、抑制纹理、增强弱边缘以及保持强边缘的目的。将本文方法与小波硬阈值增强方法、小波Shrinkage自适应阈值增强方法做实验对比，结果表明小波硬阈值增强方法虽然消除了部分噪声，但在抑制噪声的同时模糊了边缘细节。小波Shrinkage自适应阈值增强方法抑制噪声效果较好，提升了整体对比度，但边缘保持及边缘增强效果不及本文方法。本文方法在对声纳图像NSCT域进行有效的区域划分后，实施针对性的噪声消除、纹理抑制以及弱边缘增强策略，解决了传统图像增强方法存在的抑噪和边缘增强之间的矛盾，取得了比较理想的增强效果。