转子叶片气弹稳定性与强迫响应分析

韩 乐，王延荣，2

（1.北京航空航天大学能源与动力工程学院，北京100083；2.北京航空航天大学江西研究院，南昌330096）

0 引言

叶轮机械中的气动弹性现象导致叶片高循环疲劳失效，其中气动弹性失稳和强迫振动响应是2个主要方面。随着航空发动机性能的大幅提升，叶片气动负荷增大，结构更加紧凑，颤振和强迫振动响应问题愈加突出。

气动弹性失稳（颤振）是弹性系统在气流中的耦合自激振动，属于气动弹性力学中的动稳定性问题。当转子叶片发生颤振时，流体激励源于叶片振动本身，在激励与振动相互作用下短时间内振幅急剧增大，进而造成叶片破坏。目前常用的气动弹性稳定性分析方法包括能量法[1-2]和特征值法[3-4]。Erdos等[5]和He[6]将相位延迟（phase lag）法应用于气弹稳定性预测，使能量法的计算速度大幅提高；通过结合Hanamur等[7]研究的影响系数法使特征值法的分析效率显著提高；赵瑞勇等[8]和Fu等[9]利用上述方法对风扇叶片的气动弹性稳定性也进行了分析。

转子叶片强迫振动响应通常是由前排叶片尾迹或下游叶片的势扰动引起的，激励频率与转子转速和引起激励的结构特征直接相关，且不受叶片振动的影响。基于解耦方法来分析叶片强迫振动响应。Kielb等[10]将强迫响应问题的求解分为3个阶段：识别来自上下游流动的不均匀性；计算叶片非定常气动力；获取叶片振动响应。文献[11-12]中将最后1个阶段又分为非线性结构建模和柔性叶片的气动弹性响应求解。

此外，还可以采取耦合法分析叶片气动弹性问题，包括强耦合法和弱耦合法。强耦合法是将流体力学控制方程和结构动力学方程统一求解，由于2个计算域的时间和空间尺寸相差偏大，此方法求解难度较大，且计算量也极大；弱耦合法则利用每个子系统原有的求解方法，通过固体域与流体域相关边界条件的交替迭代更新数据，实现对耦合作用的模拟，虽然耗费很多计算资源，但部分学者仍采用该方法分析气动弹性问题。Sadeghi等[13]采用时域法分析了NASA67转子叶片扭转模态下的气动弹性，发现在某折合频率下叶片会出现失稳现象；徐可宁[14]自主编写了有限元程序，结合计算流体力学软件分析了错频叶盘振动的局部化现象；Espinal[15]利用弱耦合方法分析了某轴流跨声速叶片的气动弹性问题，验证了相位延迟法的可靠性。在多数情况下，由于考虑到计算能力，利用弱耦合法在多级环境中分析气动弹性问题通常仍是难以开展的。

针对上述问题，本文分别以压气机转子叶片和高压涡轮转子叶片模型为例，对气动弹性稳定性和强迫振动响应进行了分析，给出了压气机转子叶片气动弹性稳定性特征和高压涡轮转子叶片强迫振动响应特征。

1 分析方法

1.1 气动弹性稳定性分析方法

目前多采用能量法和特征值法进行气动弹性稳定性预测，由于耦合法计算量过大，难以应用于工程，一般多用于校核所发展的新方法。下面主要介绍颤振预测的能量法和特征值法。

1.1.1 能量法

假设颤振以叶片某一阶固有振型出现，通过计算1个振动周期内叶片与流场间的能量交换来预测颤振。如果1个振动周期内周围气流对叶片所作的非定常气动功总和Waero为正，则叶片发生气动弹性失稳，如果考虑机械阻尼，则机械阻尼耗散功与气动功之和决定了系统的稳定性。

基于能量法预测颤振的主要流程如下：

（1）计算叶片的固有模态，分析中可考虑稳态气动力和离心力的影响；

（2）将所关注的叶片固有模态位移映射到流场网格叶片表面上；

（3）指定流场中的叶片按照所得到固有模态振动，进行非定常流场分析；

（4）计算收敛后，提取叶片表面的力和位移，计算1个振动周期内的非定常气动功，进而得到气动阻尼；

（5）根据气动阻尼的正负判断系统气弹稳定性。

在得到叶片表面节点集中力和节点位移后，非定常气动功可表示为

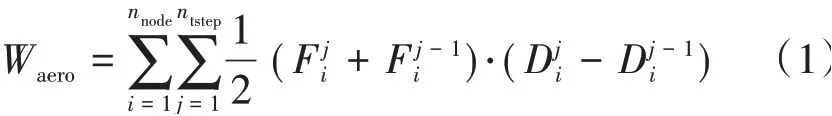
式中：i为节点编号；nnode和ntstep分别为叶片表面流体节点总数和1个振动周期内的时间步数；j为时间步编号；F为节点集中力，N；D为节点相对于叶片平衡位置的位移，m。

本文以Moffatt等[16]提出的气动模态阻尼比（Aerodynamic Modal Damping Ratio，AMDR）来表征气动阻尼的大小，基于等效黏性阻尼的概念，气动模态阻尼比ζaero可表示为

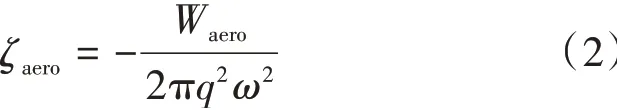
式中：q为指定模态的正则化幅值；ω为给定模态的固有振动圆频率，rad/s。

基于等效黏性阻尼的形式，可直接与机械阻尼等代数相加得到总阻尼。

在相位延迟边界条件下，通过存储1个周期内边界面上的所有信息实现对模型的简化[5]。再利用时间范畴的傅里叶级数分解见式（3），进一步避免存储周期边界上的全部信息，仅需存储傅里叶系数An就可在后处理中通过这些系数求出任意时间点的变量信息[6]。

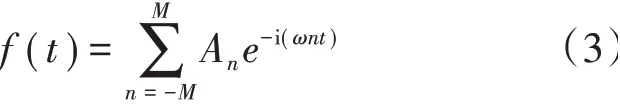
当考虑非零叶间相位角时，需要指定相邻叶片按照一定的时间相位差振动，相邻2片叶片振动时间差为

式中：σ为叶间相位角。

1.1.2 特征值法

对于调谐叶盘结构系统，不考虑机械阻尼时，物理坐标系的运动方程为

式中：u为位移向量；M、K和f分别为质量矩阵、刚度矩阵和叶片振动所引起的非定常气动力向量。

假设叶片按照简谐形式振荡u=Ueλt，并将位移幅值向量U写成模态叠加的形式，式（5）可表示为

式中：Φ为模态矩阵；q为模态位移向量；Ω为对角矩阵。

当Φ中只包含某一阶模态时，Ω的表达式为

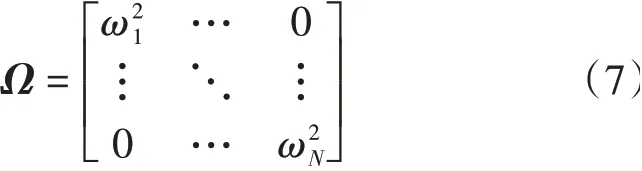
式中：Ω中各元素为叶片各阶次频率的平方。

对于调谐系统，式（7）的各对角线元素相等，每个元素代表相应叶片的固有频率，通过修改对角线元素便于引入错频。

当结合影响系数法时，式（6）中模态坐标系下的气动力向量可表示为

式中：A为模态坐标系下的气动力影响系数矩阵，代表了各叶片对参考叶片的影响，对调谐系统，A为循环矩阵，有如下形式

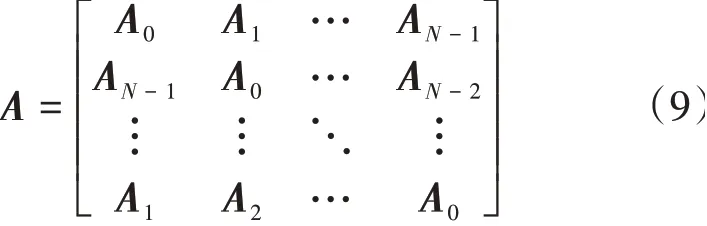
当仅考虑1阶模态时，式（9）中的各分块矩阵变为常数。将式（8）带入式（6）中，可得到如下的特征值

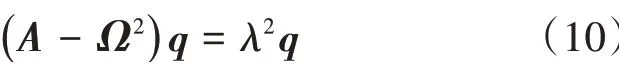
通过求解式（10）所表示的特征值，便可得到复特征值λ，其中实部代表阻尼，虚部代表频率。系统发生颤振（气弹失稳）的依据为：存在特征值满足

当Φ为质量归一模态振型时，气动阻尼表示为

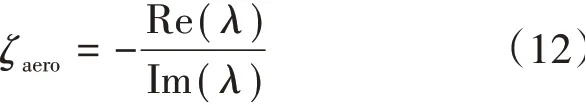
1.2 强迫振动响应分析方法

在强迫振动响应分析中，当叶片发生振动时，其表面的压力扰动主要源于上下游气流的周期性激励，而与叶片本身的变形关系不大。因此，先计算1个叶片扫掠周期内刚性叶片周围的非定常流场，再将其作为外部激励施加于叶片的有限元模型上。虽然这种假设对计算精度的影响不大，但可以极大地提高计算效率，适用于工程分析，其分析流程如图1所示。

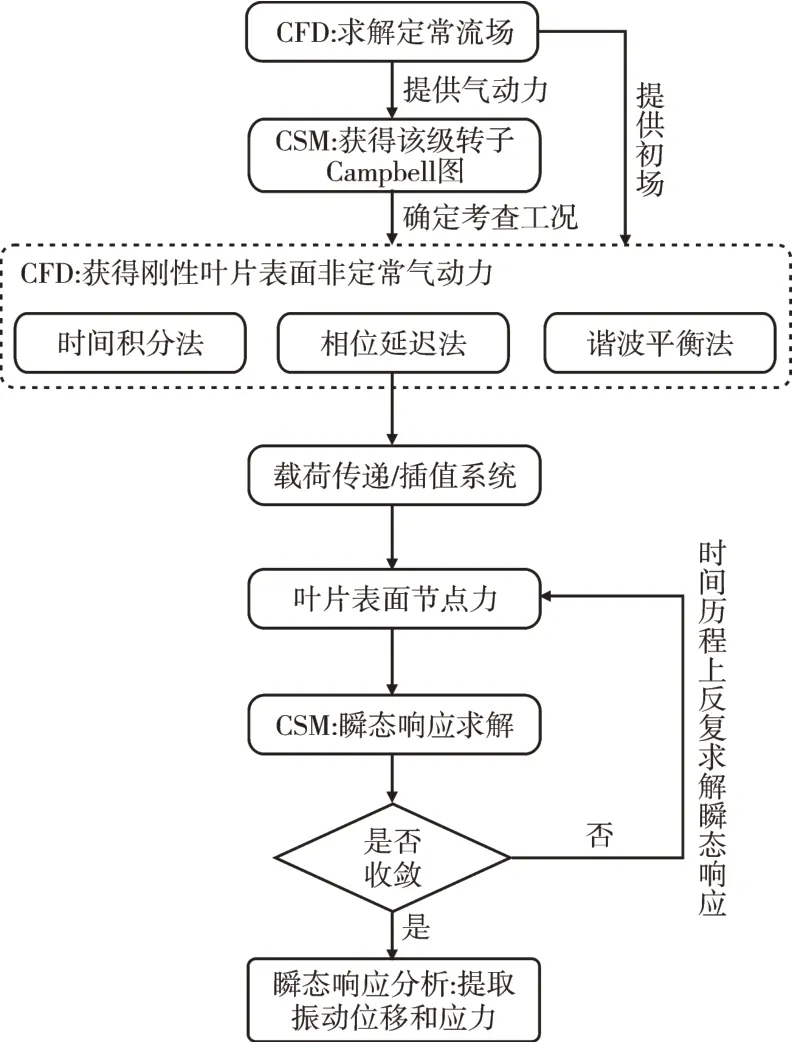
图1 强迫振动响应分析方法及流程

主要步骤为：

（1）建立叶片流体域计算模型，进行定常模拟；

（2）建立叶片有限元模型，进行模态分析；

（3）通过叶片Campbell图确定共振转速，明确重点关注的模态阶次；

（4）结合模态分析结果，找到所关注模态阶次振动应力较大的位置作为瞬态计算的监测点；

（5）分析在转静干涉作用下的非定常流场特征，并提取1个周期内叶片表面非定常气动力；

（6）计算在共振状态下叶片强迫响应特征，当振动稳定后终止计算；

（7）给出各监测点沿应力最大方向的动应力响应，利用傅里叶变换分析动应力特征。

2 压气机转子叶片气动弹性稳定性分析

2.1 计算模型

以高压压气机模型中间级的转子叶片为研究对象，相关设计和材料参数见表1。建立孤立转子叶片模型并计算在级条件下的气动阻尼，各参数包括进口总温、总压和气流角、出口静压，见表2，其子午面流道如图2所示。

表1 转子叶片的无量纲设计参数和材料参数

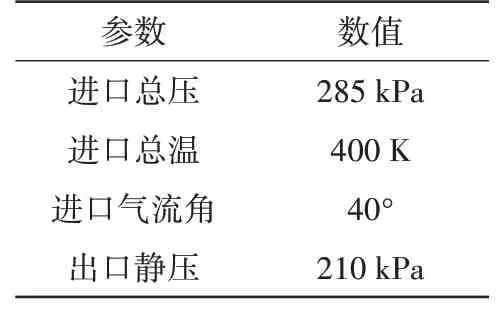
表2 级条件下进出口平均参数

图2 转子叶片及上下游流道

2.2 定常流场分析

建立转子叶片的流场计算模型，根据叶片在多级环境中的位置截取计算域，如图3所示。计算网格采用O4H拓扑结构，沿流向布置69层网格；周向布置57层网格（包括主流区33层和叶片周围O网格13层）；径向布置53层（间隙内13层）；单通道网格约为26.1万。湍流模型选择标准k-ε双方程模型，第1层网格距壁面距离为1×10-5m。进口给定总温、总压和速度方向，出口给定静压条件，相关条件由多级计算结果提取。计算结果见表3。从表中可见，转子的气动效率较高。在不同条件下叶尖流场如图4所示。从图中可见，此时为在亚声速条件下叶片全展向工作。

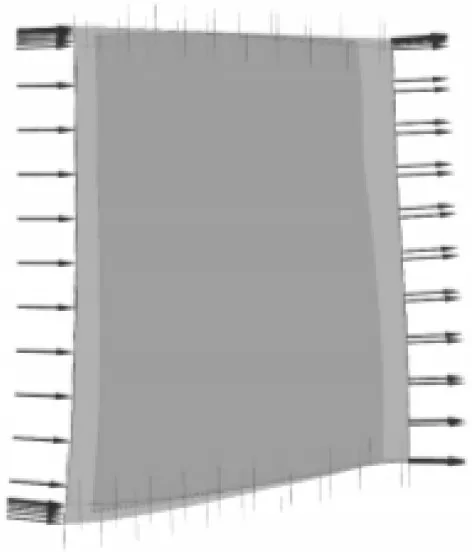
图3 转子叶片定常流场分析计算域

表3 定常流场计算结果

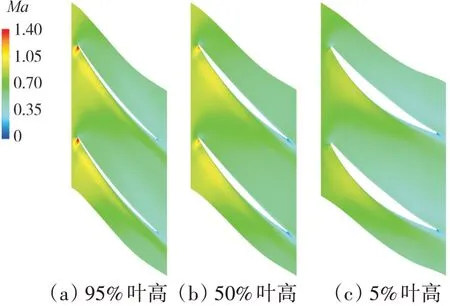
图4 典型叶高下的流场

进一步给出了多级环境和孤立转子模拟（级条件下）50%叶高截面的压力分布，如图5所示。从图中可见，压力面吻合较好，吸力面存在一定差异。其原因是在多级环境下，流动偏离设计状态并逐级放大所致。

图5 典型叶高叶片表面压力分布

2.3 模态分析

建立转子叶片有限元模型及冷热态叶型，如图6所示。从图中可见，采用8节点6面体单元，分别沿径向和弦向各布置41层和29层网格节点，厚度方向布置3层网格节点，节点和单元总数分别为3567和2240。在设计转速下的静力分析结果如图7所示。由离心力作用引起的最大静变形约为0.55 mm。随后进行含预应力的模态分析，重点考查叶尖前缘附近应力较大的振型(第4和7~9阶模态)，其振型和模态应力分布如图8所示。

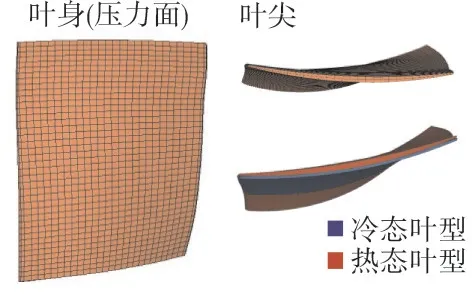
图6 转子叶片有限元模型和冷热态叶型对比

图7 叶片在离心力作用下的静变形

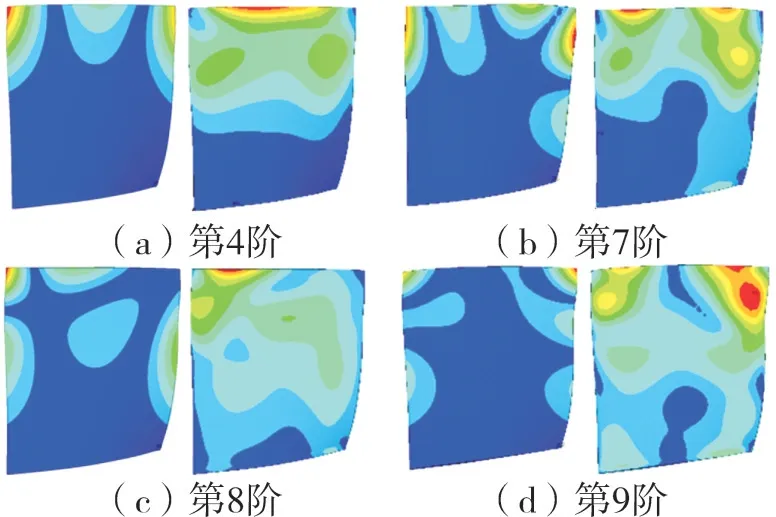
图8 转子叶片振型（左）和模态应力（右）

2.4 振荡流场和气动阻尼分析

分别采用能量法和特征值法对转子叶片的气动阻尼进行分析。非定常流场的多通道计算域如图9所示。在计算过程中指定叶片按照不同模态振动，分析各节径下的气动阻尼。在设置叶片振幅时，按照50 MPa振动应力对应的振幅进行折算，得到各阶振幅和AF值，见表4。AF=2πfA，代表了叶片的振动速度。以定常计算结果作为非定常计算的初始流场，在1个振动周期内划分60个非定常时间步，当流场参数达到稳态振荡时停止计算。分别通过式（2）和式（12）计算气动阻尼。

图9 非定常流场计算域模型

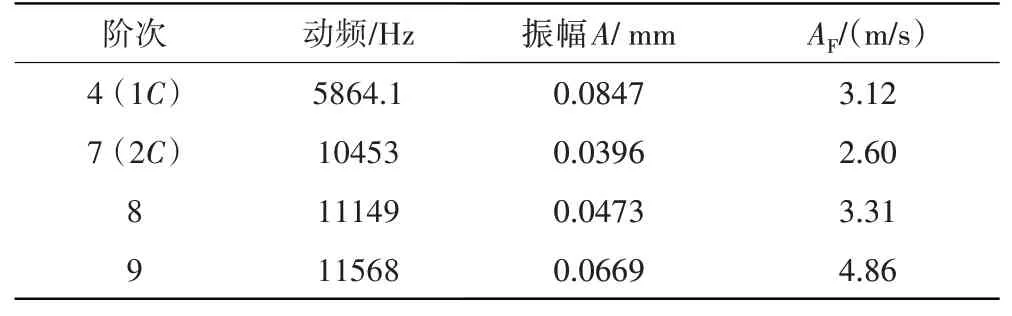
表4 在设计转速下叶片的动频、振幅及AF值

以第8阶模态为例，叶片表面非定常气动力幅值分布如图10所示。从图中可见，对高阶模态而言，参考叶片振动引起的非定常气动力主要集中在中间2~3个通道内。

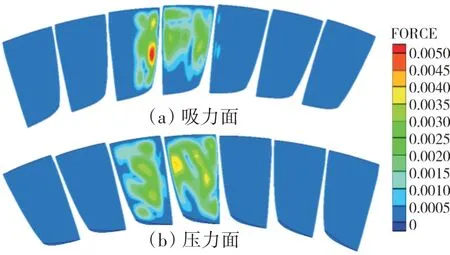
图10 第8阶模态下叶片表面非定常气动力幅值

在第8阶模态下气动阻尼随节径的变化如图11所示。从图中可见，通过2种方法得到的气动阻尼较为一致，特别是最小气动阻尼相互吻合。

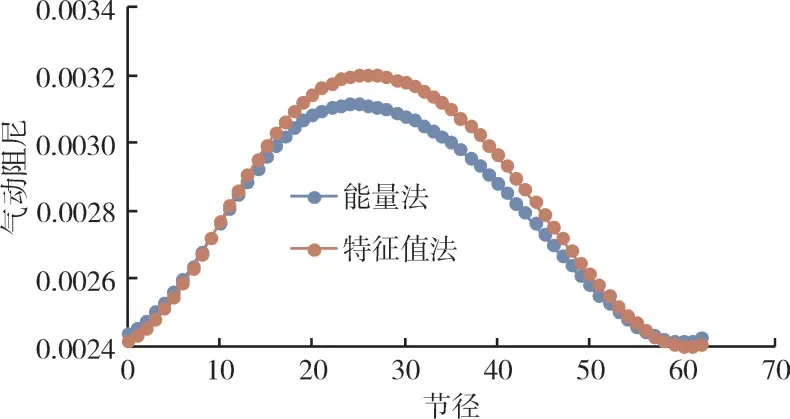
图11 第8阶模态下气动阻尼

在各阶模态下最小气动阻尼及其对应的节径见表5。从表中可见，高阶模态气动阻尼反而更小，若附近存在激励成分，可能引起较显著的振动应力。结合图8中模态分析结果，一旦激起第7、8和9阶模态，在叶尖近前缘和近尾缘区域可能出现较大的振动应力。在第4阶模态下，气动阻尼随模态频率增加而减小。因此对该转子叶片而言，需要重点关注第2阶弦向弯曲（第7阶模态）和第8、9阶模态的气动阻尼。

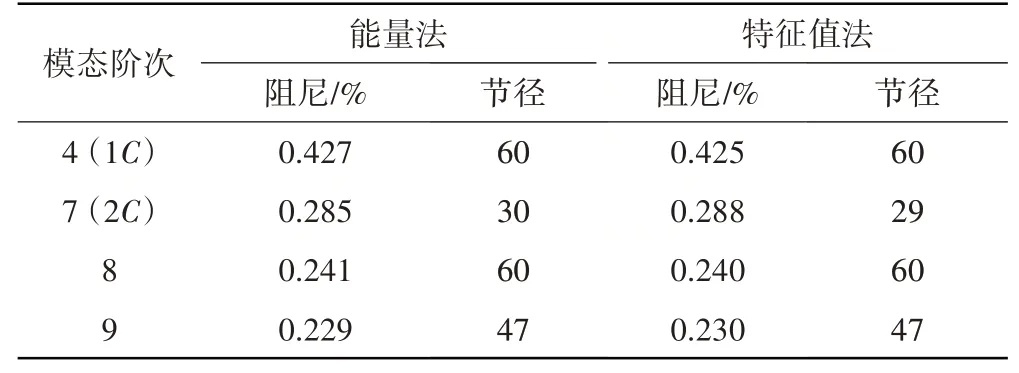
表5 不同模态下的最小气动阻尼及其节径数

同样以第8阶模态为例，最小气动阻尼所在节径下叶片表面的气动功密度分布如图12所示。从图中可见，叶身表面大部分区域气动功幅值接近0，只是在叶尖近前缘区域有1个明显的负功区。

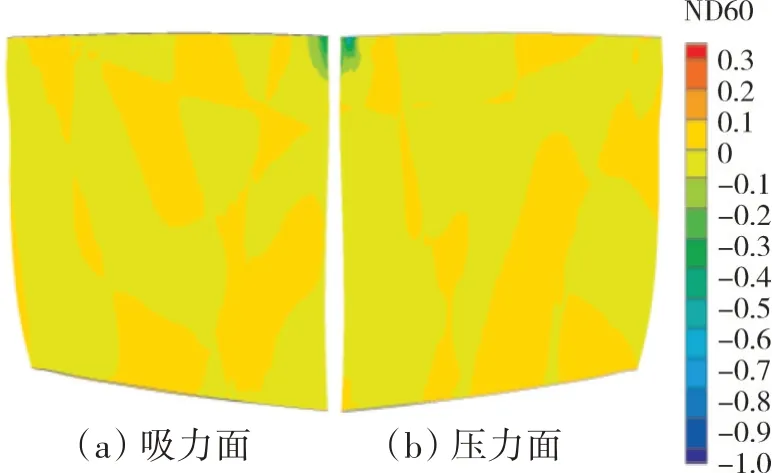
图12 第8阶模态60节径下气动功密度

3 强迫振动响应分析

3.1 计算模型

对涡轮模型的高压转子叶片进行分析，其流场计算域如图13所示。从图中可见，模型包括高低压涡轮转子、上游进口导叶和下游支板。模型中的设计参数和设计工况下的进出口边界条件见表6。4排叶片不满足约化条件，所以采用全环模型进行非定常计算。在计算域中各排叶片的网格见表7。每排叶片各通道的网格拓扑和网格数保持一致。在非定常计算中给定时间步，确保高、低压涡轮叶片均经过整数时间步后通过彼此1个叶片栅距。

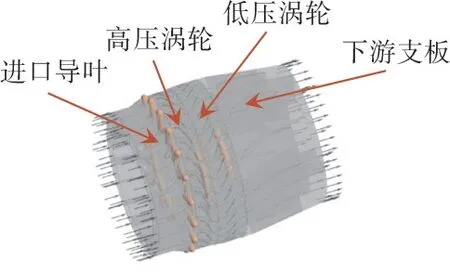
图13 涡轮叶片CFD计算模型

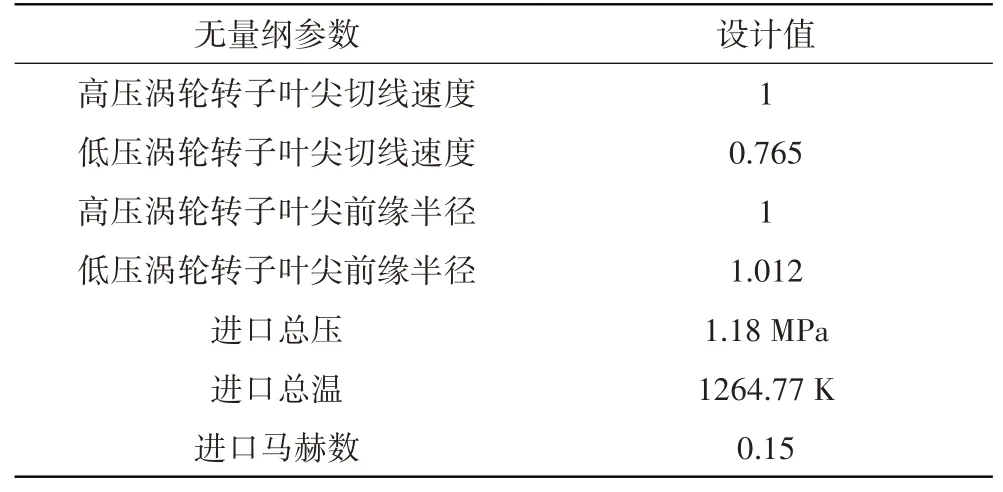
表6 涡轮转子叶片无量纲设计参数和进出口气动参数

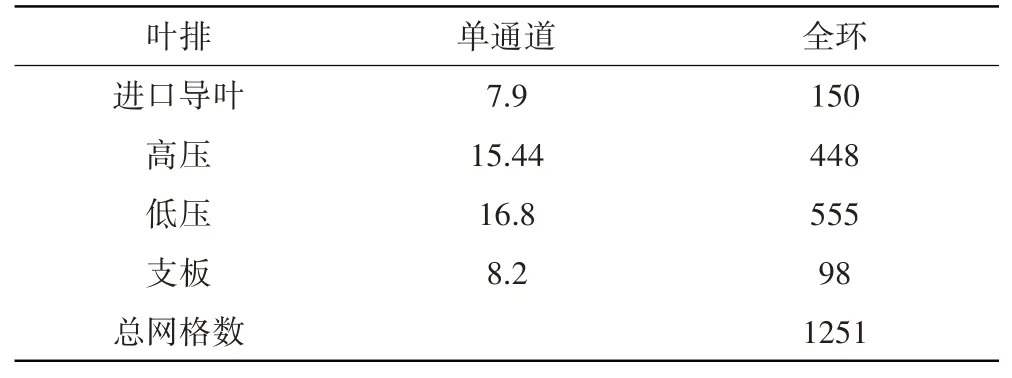
表7 各排叶片网格数 万

3.2 定常和非定常流场分析

在叶片压力面和吸力面的90%、70%和50%叶高大约10%、50%和90%弦长处分别设置压力监测点，如图14所示。为保证信号的周期性，提取压力信号完整周期进行傅里叶分析。以弦向S1位置的3个监测点为例，压力随时间的变化曲线如图15所示，此时流场中存在多个扰动成分。

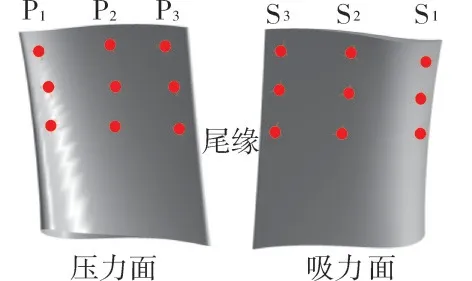
图14 叶片表面监测点

图15 监测点压力随时间的变化

以吸力面S1和S3监测位置为例，对叶片表面监测点的压力数据进行时频分析，得到频域信号如图16所示。从图中可见，主要激励为上游进口导叶（12192 Hz）及其倍频成份和在尾缘附近存在低压涡轮引起的激励（37060 Hz）。

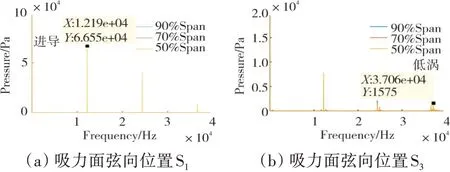
图16 监测点非定常气动力频谱分析

流场90%和50%叶高截面的相对马赫数分布结果如图17所示。从图中可见，在高压涡轮转子叶片尾缘存在明显的激波结构，导致低压叶片带来的势扰动难以向上游传播，因此高压涡轮转子叶片主要感受来自进口导叶带来的扰动，幅值可达60~70 kPa。

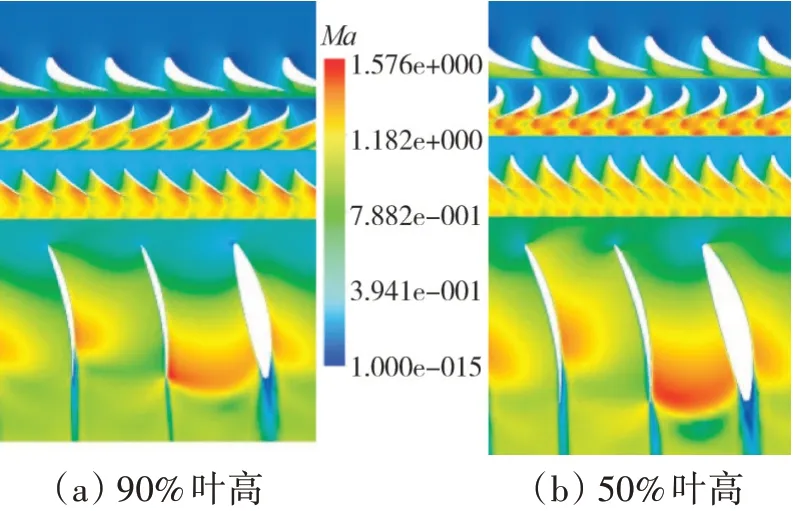
图17 90%和50%叶高截面相对马赫数分布

3.3 模态分析

基于流场模型建立有限元模型，如图18所示。通过叶片冷热态转换获得冷态叶型[17]。采用8节点6面体单元，其中节点数为3450，单元数为2552，K447A为叶片材料。

图18 高压涡轮叶片有限元模型

对高压涡轮叶片进行静力分析，在温度场和离心载荷（100%转速）作用下高压涡轮的静变形如图19所示。从图中可见，温度场形成较大的径向变形，离心力和气动力则使叶片更加“展开”，形成较大的周向变形。在几种载荷影响下，叶片最大变形均出现在叶尖尾缘区域。

图19 不同载荷下高压涡轮叶片静变形

进行含预应力的模态分析，结合前排导叶和低压涡轮的激励得到高压涡轮转子叶片的Campbell图，如图20所示。在设计转速下，进口导叶通过频率位于第4、5阶模态之间，低压涡轮带来的激励靠近第16阶模态。因此，重点关注高压涡轮叶片在上述几阶模态和激起振动所需能量较低的前3阶模态，模态频率见表8。从表中可见，离心力使叶片刚性增强，频率加大；温度使叶片固有频率降低。

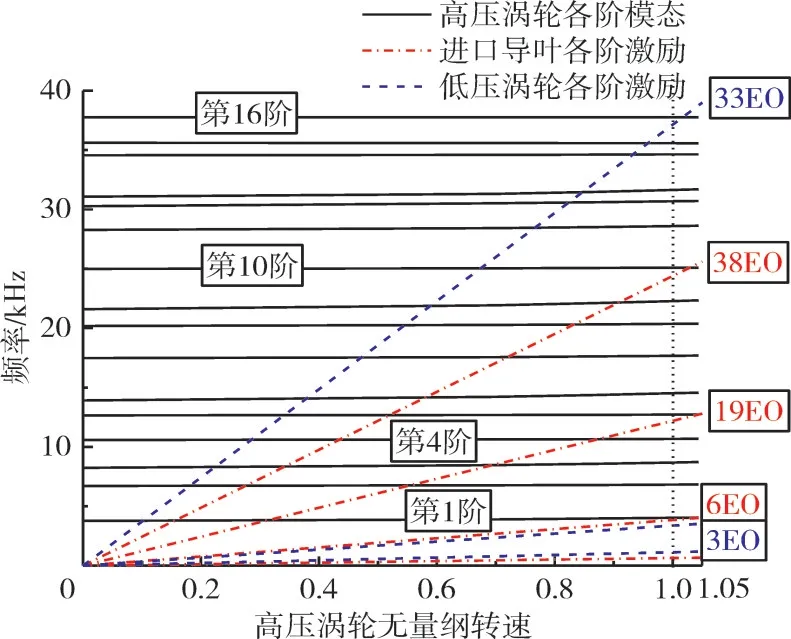
图20 高压涡轮转子叶片Campbell图

表8 高压涡轮叶片主要阶模态固有频率（Hz）和阻尼

根据模态应力较大点确定强迫振动响应分析的监测点，如图21所示。各阶模态应力和振型分布如图22所示。模拟贴应变片的方式并结合模态分析结果，根据式（13）确定高压涡轮监测点的监测方向，见表9。

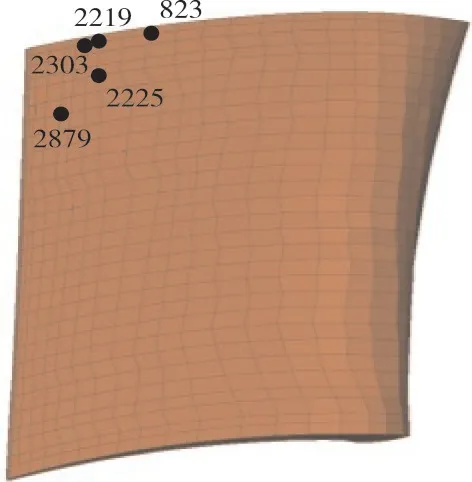
图21 高压涡轮叶片振动应力监测点位置

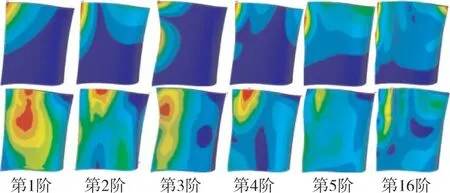
图22 主要模态阶次振型（上）和模态应力分布（下）

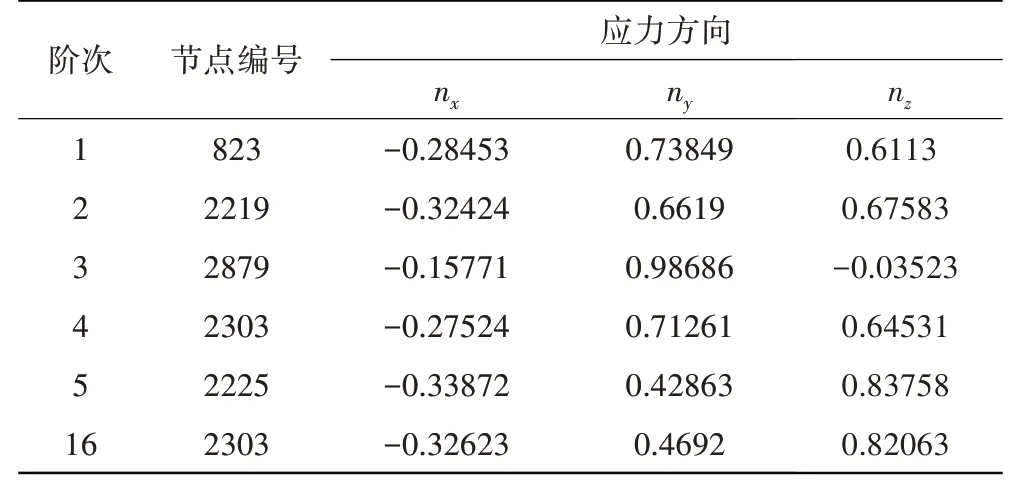
表9 高压涡轮监测点的应力方向

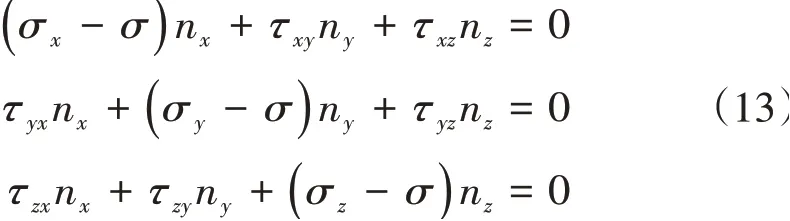
式中：nx、ny和nz为最大应力方向余弦。

由应力分量确定最大振动应力为

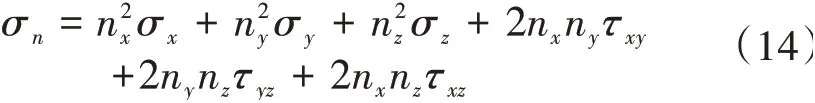
3.4 强迫振动响应分析

3.4.1 模态阻尼在瞬态响应计算中阻尼以瑞利阻尼形式给出

式中：系数α和β由任意2阶模态确定。假设该2阶模态的阻尼比分别为ζi和ζj，频率值分别为ωi和ωj，则

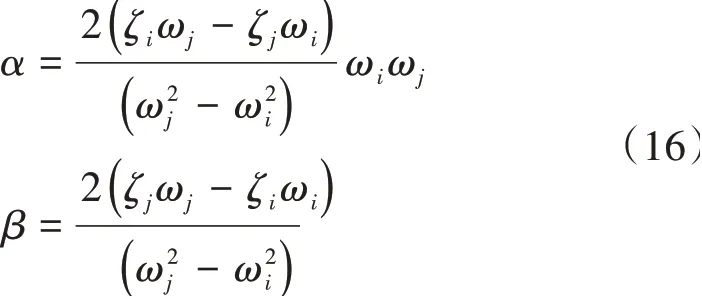
确定系数α和β后，得到任意阶模态的阻尼比

由于高压涡轮为整体叶盘结构，其结构阻尼较小，参考文献[14]，取叶片第1、2阶模态阻尼比为0.03%，此时阻尼系数α和β分别为9.55356×10-9和8.79657×10-9，由式（17）得到主要阶模态阻尼比（表8）。

3.4.2 监测点振动应力

在瞬态动力学分析中，为保证得到稳态响应解，在计算过程中首先通过设置较大的阻尼系数使瞬态响应部分在短时间内快速衰减。在计算收敛后，某监测点时域结果如图23所示。从图中可见，随着时间推进，叶片响应逐渐趋于较为稳定的周期振动，提取最后1个周期的结果用于振动应力分析。

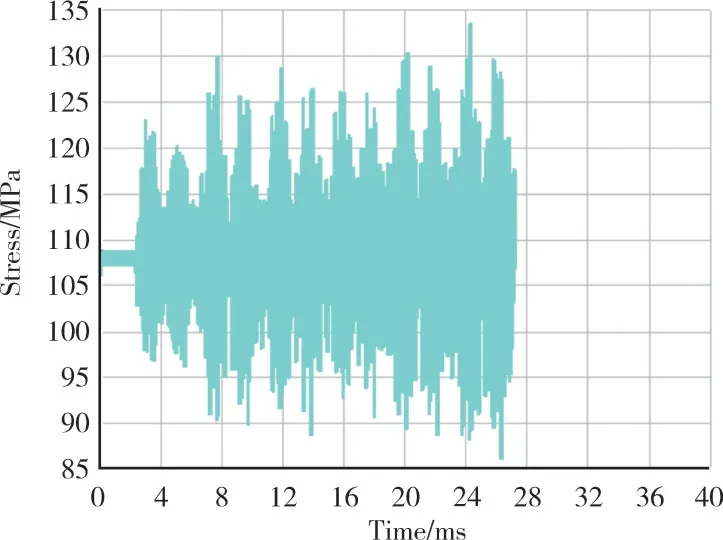
图23 瞬态响应计算监测点周向振动应力的收敛情况

以节点2879和2303为例，提取高压涡轮转子叶片监测点稳态振动应力并进行快速傅里叶变换，结果如图24所示。对高压涡轮叶片而言，振动主要由上游进口导叶引起，在低阶模态上振动较为显著。虽然激励频率更接近第5阶模态固有频率，但此时尚未达到共振状态，最大振动应力出现在第3阶模态频率下，约为12 MPa（阻尼为0.033%）。

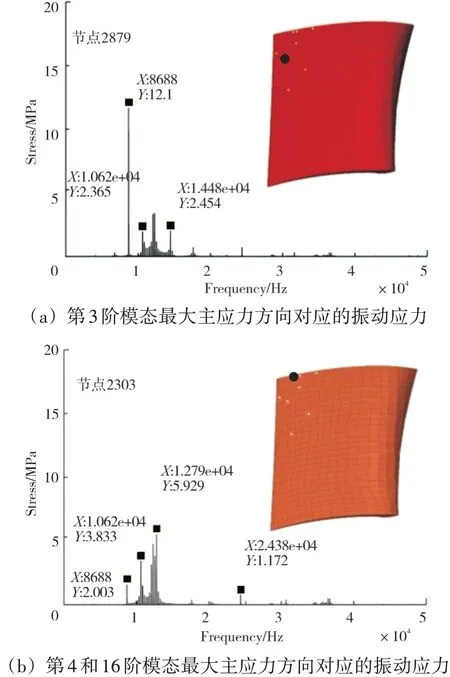
图24 高压涡轮转子叶片监测点的振动应力

3.4.3 危险模态共振状态分析

进一步分析共振状态下的响应特征。由于流场计算过于耗时，且第5阶模态共振转速较为靠近计算转速，工况偏差较小，故利用频率缩放技术对共振状态进行快速评估。由模态分析结果可知，第5阶模态危险点为图22中节点2225。对转速进行缩放，使激励与固有频率接近，得到104%转速下模态频率、激励频率和阻尼，见表10。

表10 104%转速下模态频率、激励频率和阻尼

对激励频率进行缩放，研究高压涡轮转子叶片在上述转速下的响应特征，近叶尖处监测点时域结果如图25所示。从图中可见，随着时间的推进，振动表现为明显的放大特征，表明此时激励频率与叶片固有频率十分接近。提取最后1个周期结果用于振动应力分析。

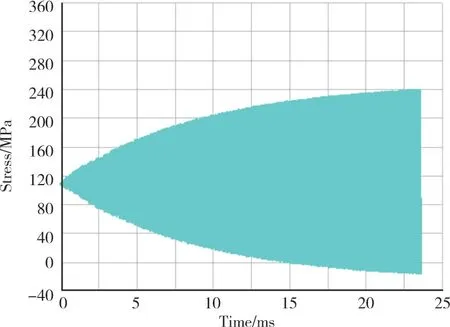
图25 104%转速下节点2225周向振动应力时域结果

对监测点的振动响应进行傅里叶分析，高压涡轮转子叶片监测点的动态应力频谱如图26所示。在104%转速下发生了第5阶模态共振，此时危险点振动应力显著增大，在0.14%阻尼下振动应力达到134 MPa。此外，对比响应和激励的频率（表10）可见，104%转速下尚未达到最大共振状态。

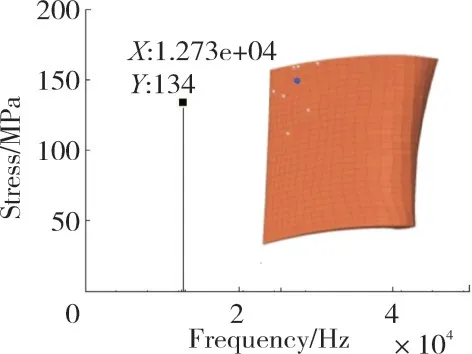
图26 104%转速下节点2225振动应力

4 结论

（1）给出了压气机转子叶片第4（第1阶弦向弯曲）、7（第2阶弦向弯曲）、8（复合模态）和9阶（复合模态）模态下的气动阻尼，采用能量法和特征值法得到的计算结果有较好吻合性。高阶模态（第7~9阶模态）对应的气动阻尼相对更小，叶身表面大部分区域非定常气动功幅值接近0，只是在叶尖前尾缘区域存在较明显的负功区，提供正阻尼。

（2）结合振型和应力分布分析，如果在激起叶片第7、8和9阶模态振动，或者在这3阶模态下发生气弹失稳，叶尖前尾缘区域振动应力较大，易引起疲劳开裂。

（3）利用强迫振动响应分析方法对高压涡轮叶片进行了分析，主要受上游进口导叶的影响，其带来的非定常气动力可达60~70 kPa，可能激起叶片第5阶模态。当发生第5阶模态共振时，振动应力可达134 MPa（阻尼0.14%）。