基于粒子系统的船行波三维仿真
2021-08-27王怀兵陈姚节
王怀兵,徐 新,2,3,陈姚节*,2,3
(1.武汉科技大学 计算机科学与技术学院,湖北 武汉 430065;2.智能信息处理与实时工业系统湖北省重点实验室,湖北 武汉 430065;3.冶金工业过程国家级虚拟仿真实验教学中心,湖北 武汉 430065)
0 引 言
船行波是船舶在海面上航行时与海面及波浪撞击所产生的一系列浪花飞溅、液滴、气泡等各种现象形成的水面波。按照船行波所产生的位置不同,可以将船行波分为船首浪和船尾浪。由于船行波是一个非常复杂的水面波,极大地受船舶运动、船舶形态、风、水流速度和方向以及海面上的波浪等因素的影响,没有光滑、好定义的表面,其运动形态既有规律性又有随机性,在构成与动力学、光学交互等方面又非常复杂,所以一直以来针对船行波的三维仿真是一个复杂的问题,不能使用一个简单的模型来对其进行仿真。近年来,随着计算机与虚拟仿真技术的不断发展,对于船行波的模拟仿真在许多领域得到了广泛的应用,但是如何更加逼真地对船行波以及船舶浪花进行仿真仍是一个难点,需要重点研究。目前对于船行波的仿真主要分为以下几个方向。
最简单的实现方法是利用粒子系统的特性,仅仅在视觉上实现船行波的效果,马天等人使用该方法进行了实现[1]。但由于该方法在视觉上实现了船行波的浪花效果,并没有实现船舶与海面的交互效果,所以仿真的效果不够真实。为了获得真实的仿真效果,研究者们基于船行波运动的物理规律,提出了基于物理模型的船行波模拟方法,Landrini等人[2]、王顺利等人[3]通过该方法进行了实现,但由于这种方法计算过于复杂,无法满足实时性的要求。还有一种方法则是通过分析船行波的数学模型,通过简单的计算得到船行波航迹,再采用粒子系统加以渲染。Michael E.Goss[4]、赵欣等人[5-6]使用这种方法进行了实现,在一定程度上简化了计算,实时性较好,但是仿真效果却不够真实。
该文基于最后一种方法,给出了一种新的船行波仿真方法。首先通过分析船舶尾流的几何特征,求解了尾流宽度与船舶宽和船舶航速之间的关系,并通过粒子系统来搭建船尾浪的粒子运动模型,完成了船舶尾浪的模拟,实现了船舶尾浪的浪花破碎效果。对于船首浪,则简单地使用粒子系统建立粒子系统的运动模型来模拟船舶首部与海浪碰撞所产生的浪花破碎与飞溅等的效果。
1 船艏浪粒子系统建模
由于文中是要在Unity引擎中对船行波进行仿真,所以坐标系的选取以Z轴为船舶前进、后退方向轴,X轴为船舶向左、向右转弯方向轴,Y轴为船舶的上下方向轴。
船首浪是由于船首与海面相碰撞而形成,且经过碰撞所形成的船首浪应该是一个三维效果[7],即在水上与水下都会产生。
但是在视觉上,一般只能够看到在水面上的波浪[8]。所以为了方便模拟,在模拟船首浪时只考虑在水面上的船行波。
首先对船首船行波的粒子系统进行初始化,以船首最顶端的坐标为原点(0,0,0),船首的高度为h,船舶的长度为L,海平面高为H,所以船首到海平面的投影交点为o点,其坐标为(0,H-h,0),通过计算获取船舶与海面相交点的坐标,就可以得到o点到船首与海面相交点的距离R。由于在Unity中以Z轴为船舶前进方向,X轴为船舶转弯控制轴,所以船首粒子发射的初始位置为:

(1)
确定粒子初始位置后,向船首每次发射4 000个粒子。粒子的初始速度为:
(2)
式中,V为粒子发射的初始速率,是一个标量,其大小与船舶航速有关,船速越大V越大;θ为粒子速度矢量与xoz平面的夹角,范围为(0,π/2);β为粒子速度矢量在xoz平面中的投影与x轴的夹角,范围为[20°,70°]和[-70°,-20°]。
为了求解海浪与船舶首部的碰撞,就需要对碰撞进行检测,由于在此处使用的是粒子系统,所以这个检测就可以转化为粒子与多边形的碰撞检测[9-10],也就是检测海浪粒子在运动过程中是否会与代表船舶外边界的多边形发生碰撞。将海浪粒子看成是一个理想的刚体,船舶首部碰撞后做反弹运动,如图1所示。

图1 粒子碰撞示意图
图中n为粒子与船舶碰撞点相对于船舶首部边界的法向量,P点表示粒子在t时刻所在位置,若粒子未与船舶发生碰撞,其就会沿着以前的方向继续前进,直至生命周期结束[11]。当粒子与船舶发生碰撞,那么在理想状态下粒子经过反弹应该是运动到P1点,但是由于存在粘滞力,以及其他相关因素的影响可能只能够运动到P2点所在位置。为了模拟出这种能量损耗的效果,令碰撞后的速度大小为原来的0.8倍。
粒子在发射出去或者碰撞结束后只受重力的影响,主要在做自由落体运动,所以粒子的初始加速度为:ay=g,在运动t秒后,船舶将由(X,Y,Z)运动到(x,y,z),且(x,y,z)的值应该为:
(3)
当粒子的y运动到H时,控制粒子消失并重新初始化。
2 船艉浪粒子系统建模
船尾浪是由于螺旋桨的击水作用与海水的填充而产生的涡流以及环流效果,其中涡流的扩散会形成浪花,以及泡沫破碎,使得船舶尾部会形成很明显的船舶尾迹[12]。由于船舶的尾迹产生很复杂,所以为了简便,主要根据实际的观察与船舶航行时的照片及视频来根据船舶尾浪的几何特征进行分析,通过分析发现船舶尾流的几何特征主要集中在其边缘特征[13]。其产生的船尾航迹整体向后倾斜,然后垂直于航向。因此定义指向船舶尾流边缘的切线与船速的夹角为扩散角。其特征为靠近船尾的扩散角约为50°,但是角度在20 s到30 s后降低到1°[14]。船舶尾流的最大长度等于船舶航速乘以船舶尾流持续时间,而船舶尾流持续时间则与海面上的环境有关,一般为120 s[15],即L=Vc*T。建立一个坐标系,如图2所示,原点位于船舶尾部的一侧交界处。

图2 船舶尾流分析图
假设尾流的扩散速度为Vp,船舶航行速度为Vc,则通过图2可以看出尾流的扩散速度与船舶航速是相互垂直的关系,并且扩散角β和Vp,Vc之间的关系为:
(4)
由诺贝达法则,对分式上下两部分分别求导可以得到:
(5)
根据式(5)可以求出尾流的扩散速度:
Vp=Vc•tanβ
(6)
扩散角β通过分析已经知道了其开始时为50°,经过20秒后为1°,因此可以将扩散角β定义为:
(7)
实际上,尾流的扩散速度还需要受到波浪等海面的环境因素以及水的粘滞性等因素的影响[16],但是为了计算的简便与快速,该文将这些因素的影响进行简化。所以t时刻的船舶尾流宽度W(t)的求解公式如下:

(8)
式中,c为影响因子,其大小与海水的粘滞性以及海面的环境影响等因素有关,一般在(0.3,0.8)之间;B为船舶的宽度。由式(6)~式(8)可以得到式(9)。
(9)
通过公式可以发现船舶尾流的宽度与船舶航速有很大的正相关关系,且与船舶宽度有一定的关系。
为了实现船舶尾迹的模拟,接下来将使用粒子系统进行仿真,利用粒子系统对船舶尾迹进行建模。
以船尾与海面相交点为粒子发射中心生成一个半径为1的锥形粒子生成器,所以粒子的初始位置为:
(10)
式中,L为船舶的长度,lc为船尾与海面相交点与船尾顶点到海平面投影之间的距离。
在确定粒子的初始位置后,粒子的初始速度为:
(11)
式中,V为粒子发射的初始速率,是一个标量,其大小与船舶航速有关,船速越大,V越大;θ为粒子速度矢量与xoz平面的夹角,范围为(0,π/2);β为粒子速度矢量在水平方向上与z轴的夹角。
由于粒子在发射出去后只受重力的影响,主要在做自由落体运动,所以粒子的初始加速度为:ay=g。粒子在运动t秒后,船舶将由(X,Y,Z)运动到(x,y,z),且(x,y,z)的值应该为:
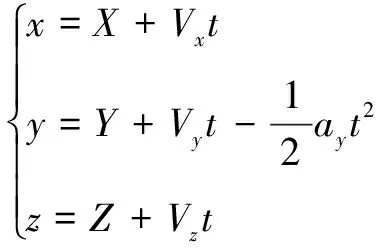
(12)
当粒子的高度y运动到H时,或者宽度达到式(9)中W(t)时,控制粒子消失并重新初始化。
3 基于Unity的船行波实现与分析
3.1 基于Unity粒子系统的船行波实现
在Unity中对于粒子有着很好的封装,可以方便地创建与控制。对粒子的控制方式主要可以分为在Unity控制面板中直接控制和通过编写脚本进行控制,文中则是通过编写脚本对船行波粒子进行控制,具体步骤如下:
(1)根据船舶的位置、航速等信息初始化粒子的生命周期、初始位置、初始速度、加速度等粒子的基本属性。
(2)根据当前航速计算船尾浪粒子系统的边界。
(3)根据t时刻加速度更新速度和粒子位置。
(4)判断粒子是否与船首发生碰撞,若发生碰撞则更新粒子运动方向和速度大小,若没有发生碰撞继续执行。
(5)判断粒子的位置是否超出步骤(2)求出的边界或者粒子已经达到了最大的生命周期,如果没有继续执行步骤(3),否则执行下一步。
(6)删除超出边界或者达到最大生命周期的粒子,并添加新的粒子。
(7)绘制粒子系统的图像。
3.2 实验结果与分析
文中是基于Unity引擎和VS2017平台进行船行波的仿真。仿真实验的硬件配置:CPU为Inter Pentium N3540/2.16 GHz;4.0 GB内存。显卡为NVIDIA GeForce 920 M;硬盘为186 GB/263 GB。软件信息:操作系统使用的是Windows 8.1 64位操作系统,使用Unity2018作为实验的运行测试环境,同时使用VS2017作为脚本开发环境。
通过第2节船尾浪的建模可以发现,船舶尾浪的宽度与船舶宽度以及船舶航速和时间有关,但其与船宽的关系与时间无关,所以着重考虑船尾浪宽度与时间和航速的关系。实验中所用的船舶为集装箱船,参数为船长140米,船宽25米,型深11.5米,设计吃水8米,设计航速为14节(1节约等于1.85 km/h约等于0.5m/s)。假设式(9)中的c=0.6,可以计算出在不同航速,粒子发射后的不同时间的船舶尾浪宽度,20秒之后船舶尾流宽度变化极小,可以忽略,如表1所示。

表1 船尾浪宽度
图3和图4是船舶航速为10节时,船舶分别做回旋运动和Z型运动时的截图,可以发现在做回旋实验与Z型实验时尾流也没有出现很大的变形与失真的现象。

图3 船舶做回旋运动(V=10节)

图4 船舶做Z型运动(V=10节)
而图5~图7则是在同一视角下的船舶速度分别为2节、4节、10节时的船舶直航的截图。通过对比可以发现,随着速度的增大,船舶尾流的宽度也在增大,符合表1的规律。并且在实验中船尾浪所设置的最大粒子数量为30 000个,计算出来的帧速率平均在每秒52帧左右,可以满足海洋环境仿真的实时性要求。

图5 船舶直行(V=2节)

图6 船舶直行(V=4节)

图7 船舶直行(V=10节)
4 结束语
文中提出了一种新的船行波仿真方法,与现有的方法相比,通过分析船舶尾流所表现出来的几何特征,并进行一定的求解获得船尾浪的宽度与速度,时间以及船舶宽度的计算公式,并使用粒子系统来搭建船尾浪的粒子运动模型,实现了船舶尾浪的模拟。实验所模拟的船行波的视觉效果更加符合现实中的船行波的表现效果,并且易于实现,且拥有较好的实时性。
但是由于实验仅仅使用粒子系统对船行波进行模拟,相对比较简单,并没有实现船舶与海面交互所形成的波的计算,所以在真实性方面有一定的差距,并且没有考虑一些现实中的其他因素对船行波的影响,因此还有待完善与修改。下一步将针对船舶与海面交互方面进行进一步的研究,并考虑海洋中的环境因素,如天气、海浪等对船行波的影响,进一步提高船行波仿真的模拟效果,提高模拟的真实度。
