基于树形奇偶机的密钥交换优化方案
2021-08-26韩益亮
韩益亮 李 鱼 李 喆
(武警工程大学密码工程学院 西安 710086)
1 引言
人工智能技术与各个领域的交叉结合越来越紧密,与密码学的融合也在不断加深。一方面,人工智能技术本身存在的安全隐私问题可以利用密码学的方法和工具来解决[1];另一方面,人工智能技术也可以用于密码算法的设计与分析[2]。其中,利用互学习神经网络设计密钥交换不需要耗用大量计算资源,在无线传感器网络、无人机、云计算等领域有良好的应用前景。将神经网络同步用于设计密钥交换是Kanter等人[3]首次提出来的,其具有速度快、安全性高的优势,但随着几何攻击、合作攻击等分析方法的提出,尽管其可以通过增大参数来保证安全性,但参数增大带来了效率的降低。因此采用新技术提高神经网络同步的效率和安全性是目前亟待解决的问题。
Kinzel等人[4]的研究表明了单个感知机之间的同步易于被攻击者模仿而不适合用于实现密钥交换。Klimov等人[5]对Kanter等人[3]提出的神经密钥交换协议进行了详细的分析,并提出了遗传算法攻击、几何攻击和概率攻击,以上3种攻击能有效攻破神经密钥交换协议,但仅限于固定的参数。当参数增大时,Shacham等人[6]提出了一种合作攻击的策略,和单个攻击效果最好的几何攻击相结合,能够使攻击者的成功概率不受神经网络突触深度的影响。Ruttor等人[7]提出了一种基于神经网络权重查询的方式来代替随机输入,能够降低合作攻击的成功概率。Allam等人[8]提出了将预共享密钥作为学习边界的认证神经密钥交换协议,并采用动态的学习率,使得攻击者在不知道预共享密钥的情况下,无法采用遗传算法攻击、几何攻击和概率攻击得到想要的结果。Pal等人[9]为了解决现有基于树形奇偶机(Tree Parity Machine,TPM)的密钥交换中同步时间不够高效和密钥随机性不够强的问题,提出了一种新的同步学习规则,该学习规则在通信双方TPM输出结果相等时更新权重,然后各自将权重与系统当前时间进行模运算。其仿真结果表明,Pal等人[9]提出的新方法与Hebbian,Anti-Hebbian和Random-Walk学习规则相比,能够有效减少同步所需时间。Dong等人[10]将TPM从实数域扩展到复数域,相应的权值、输入和输出也都扩展为复数,并给出了复数域下TPM的相关定义和学习规则,然后设计了基于复数域下TPM的密钥交换协议。
Sarkar[11]将基于多层感知机同步产生的会话密钥应用到无线通信网络中,提出了一种新的加密算法。Sarkar等人[12]提出用TPM之间的同步生成可变长度的会话密钥,并从会话密钥中派生出子密钥串用于设计初始密码矩阵,对明文进行加密。肖成龙等人[13]提出了一种采用人工神经网络的双重加密方案,主要利用人工神经网络产生随机矩阵来对数据进行第1次加密,从而提高通信系统抵抗暴力攻击的能力。Saballus等人[14]提出了两种基于完全二叉树的多神经网络同步算法,并将其应用到了基于神经网络的群组密钥交换中。Santhanalakshmi等人[15]基于神经网络分别设计了环结构(采用邻居学习同步模式)和树结构(采用分布式同步模式)的组密钥协商协议,这两类协议都可以用作动态对等组的密钥协商,支持旧用户撤销和新用户加入,且均能保证前向安全、后向安全和密钥独立。
一般的树形奇偶机没有使用向量计算,效率不高。Chourasia等人[16]在TPM实现时用NumPy库进行向量化,提出了向量化的神经密钥交换协议,并深入研究了向量化后的TPM结构参数对同步时间的影响。该文还提出在密钥生成过程中使用消息认证码来实现认证性。Walter等人[17]采用Python实现的几何攻击算法来寻找TPM的最佳结构,即寻找使得神经密钥交换安全性更高的TPM的最佳参数组合,他们的研究表明参数为(8,16,23)时在抵抗几何攻击上效果最佳。由于文献[17]的研究使用的是采用几何攻击策略的单个攻击者,而不是采用合作攻击策略的多个攻击者,其方案的安全性还有待进一步研究。
本文的主要贡献在于:定义了向量化的学习规则,提高树形奇偶机同步学习的时间效率;给出了寻找在时间和安全性上更优的TPM结构参数的方法,并将采用优化参数的本文方案与文献[17]、文献[18]进行了效率对比;将向量化方法与文献[16]的方法进行了对比;同时,研究了向量化对同步步数和同步时间的不同影响。仿真结果表明,采用向量化学习规则和优化参数的本文方案在时间效率上优于文献[17]、文献[18]中的方案,且采用向量化的学习规则只是减少了同步所需要的时间,没有减少同步所需步数,不会导致攻击者的成功率增加,因而不会影响优化方案的安全性。
2 预备知识
2.1 树形奇偶机
树形奇偶机[19]是具有一个隐藏层的前向反馈神经网络(见图1),能够用于神经密钥交换协议的设计。树形奇偶机由K个隐藏单元组成,每个隐藏单元有N个输入神经元和1个输出神经元。
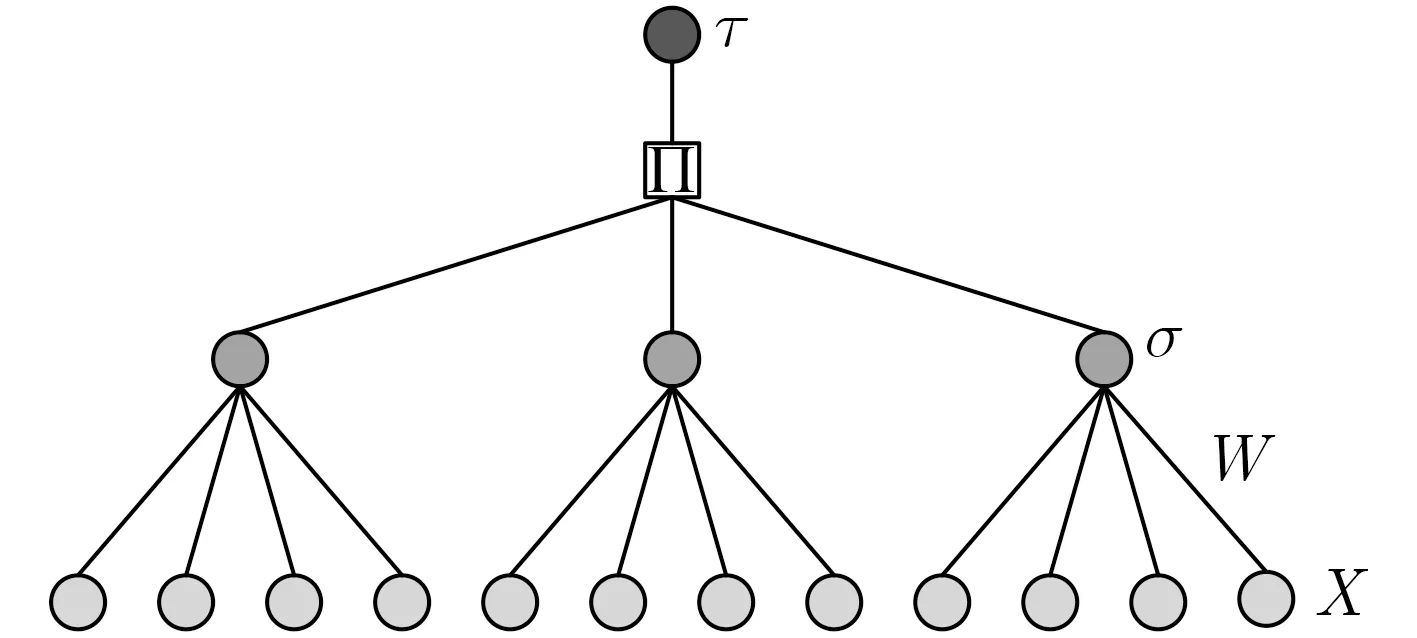
图1 K=3和N=4的树形奇偶机
每个输入神经元的取值范围:xi,j∈{−1,+1},每个输入神经元所对应权重的取值范围:w i,j∈{−L,−L+1,···,+L},其中i=1,2,···,K表示树形奇偶机的第i个隐藏单元,j=1,2,···,N表示隐藏单元的第j个 输入,L表示隐藏神经元权重可取的最大值。每个隐藏单元的输出为σi=sign(h i),其中h i−1h i=0
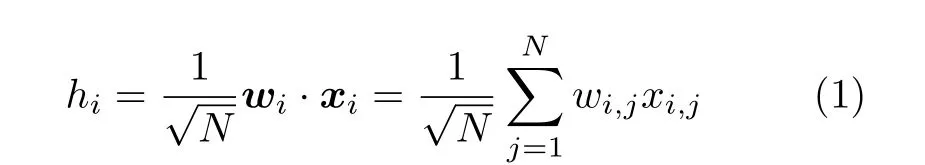
的取值有3种,分别为 ,0,1,当 时,

2.2 学习规则
在开始进行密钥交换时,Alice和Bob各自运行一个树形奇偶机,双方随机选择互不关联的初始权重wA和wB。在同步过程中,双方都将公共参数x作为共同输入,并将输出结果τA或τB发送给对方。在收到对方发送的输出结果后,判断τA和τB是否相等,如果相等,则按照以下学习规则进行权重的同步更新;否则,不对权重做任何改变。
Hebbian学习规则[20],更新权重方式

2.3 几何攻击
几何攻击是由Klimov等人[5]在2002年亚密会上提出的,每个几何攻击者各自进行独立攻击,互不影响,目的是和通信双方实现权值同步。其具体思想是攻击者Eve采用和通信双方Alice,Bob一样的树形奇偶机结构,随机地初始化自己的权值,在每一个学习步采用和Alice,Bob一样的输入,然后根据以下策略更新自己的权值,以为了和Alice实现权值同步为例。
步骤1如果Alice和Bob的输出不相等,即τA=τB,那么攻击者Eve选择不更新自己的权重。
步骤2如果Alice和Bob输出相等且和攻击者Eve的输出相等,即τA=τB且τA=τE,那么攻击者Eve按照和Alice一样的学习规则更新自己的权重。
步骤3如果Alice和Bob的输出相等,但是和攻击者Ev e的输出不等,那么攻击者Eve寻找

3 基于向量化学习规则的神经密钥交换方案
3.1 模型描述
本文采用特殊的神经网络即向量化树形奇偶机(vectorized Tree Parity Machine,vTPM)来进行Alice和Bob之间的密钥交换,将通过相互学习实现同步后的vTPM权值作为会话密钥,其同步过程如下所示:
步骤1 Alice和Bob各生成随机权值对vTPM进行初始化,接着进行以下步骤直至完全同步;
步骤2生成随机输入向量;
步骤3利用随机输入向量计算各隐藏层的输出值以及vTPM的输出值;
步骤4 Alice和Bob将自己vTPM的输出结果发送给对方;
步骤5在收到对方的信息后,判断自己的输出结果和对方的是否相等,如果相等则采用相应的学习规则更新权值;否则,跳转到步骤2执行。
本文在步骤5中采用的学习规则是向量化的,即可以并行执行的学习规则。以Alice为例,其通过向量化Hebbian规则更新权重的方式为
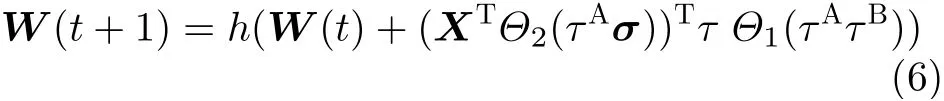
通过向量化Anti-Hebbian学习规则更新权重的方式为

通过向量化Random-Walk学习规则更新权重的方式为
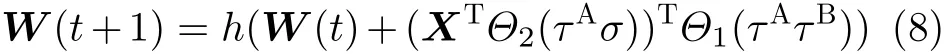
其中,t表示当前时间步,t+1表示下一时间步,函数Θ1用于比较双方输出结果是否相等,如果相等,即τA=τB则返回1,否则返回0。函数Θ2返回的结果为向量[ (0/1)1,(0/1)2,···,(0/1)K],其作用为比较σ1,σ2,···,σK分别与τA是否相等,如果相等,则在向量对应位置返回为1;否则,在向量对应位置返回为0。函数h(W)将 任意w∈W的值保持在−L和 +L之间。如果权值超出区间,那么通过h(W)函数将权值w∈W设置为±L。
3.2 参数设置
本节主要通过参数预处理找出用于生成约512 bit长度密钥的v TPM结构参数。表1给出了相关变量及其描述。

表1 变量说明
v TPM的结构是由其参数K,N,L决定的,用vTPM生成加密密钥的长度也是由K,N,L三者决定的。加密密钥长度=K×N ×LBIN,其中LBIN表示L的二进制值的比特长度,因为权重范围{−L,−L+1,···,+L},所以用有符号数表示L,即LBIN中有1位是符号位。当L=1时,LBIN=2;L=2或3时,LBIN=3;当L=4或5或6或7时,LBIN=4;当L不断增大时,以此类推。为了找到最适合生成512 bit长度密钥的vTPM结构,首先需要找到所有可能的K,N,L的值。由于K≤3时很容易被合作攻击攻破,因此本文中不考虑K≤3的情况。并且严格限制K≤N,因为当K>N时,两个树形奇偶机之间的同步将会变得困难。又因K,N,LBIN不全是512的因子,所以存在部分K ×N ×LBIN的值略大于512。
通过参数预处理发现,当K增至14时,由于K≤N的限制,N=14已是N所能取的最小值。在K>14并继续增大时,N的值也随着K的增大而同步增大,而同步时间也会随着增大。而预处理也发现当K增至14时,相应的参数组合已经完全能够抵抗几何攻击和合作攻击了。因此,本文的参数组合仅考虑K在4~14,一共有25种组合。具体的参数组合如表2所示。
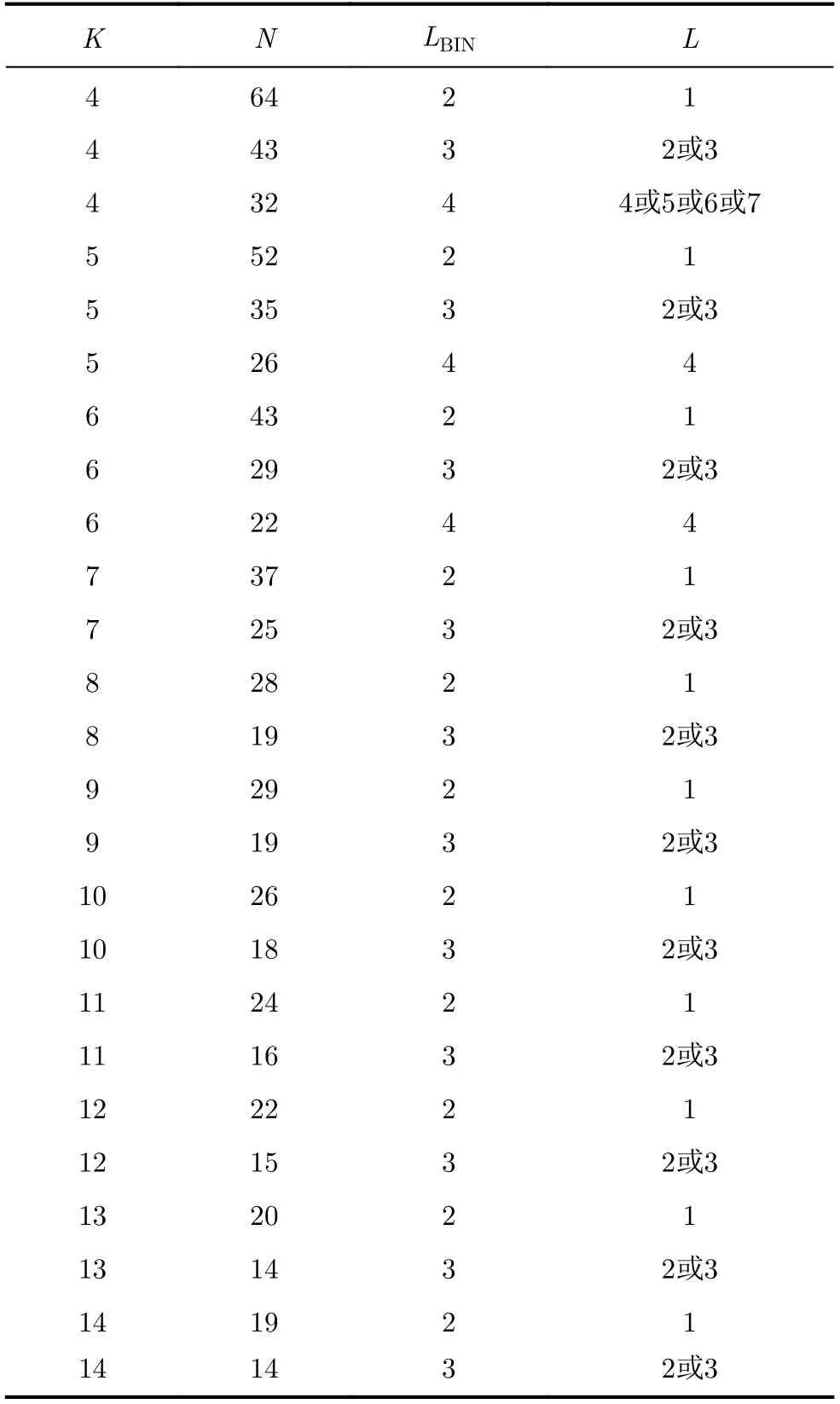
表2 参数组合
3.3 效率测试算法
本节主要设计了用于测试神经密钥交换所需时间的算法。本算法主要测试的是通信双方Alice和Bob在采用树形奇偶机进行相互学习所需的步数和对应的时间。具体过程如表3中算法1所示。

表3 效率测试算法(算法1)
在算法1中,第(1)行是用于记录运行总时间和总步数的,第(2)行是需要执行的次数,第(3)~(6)行是用参数K,N,L对vTPM进行初始化以及初始时间和初始步数。第(7)行是进行仿真直到Alice和Bob实现同步,第(8)行是生成随机输入向量。第(9)~(10)行是计算Alice和Bob的vTPM的输出。第(12)~(14)行是对输出满足条件时进行权重更新,并增加1次步数,进入下一次循环。第(15)~(21)行是计算平均时间和平均步数。
3.4 安全性分析

Alice的隐藏层输出不相等的有1个或者3个。有1个隐藏层输出不相等发生的概率为25%,而有3个隐藏层输出不相等的概率也为25%。因此有1个隐藏层输出不相等和有3个隐藏层输出不相等发生的概率是相同的。几何攻击仅针对有1个隐藏层输出不相等而采取相应的策略,忽略了有3个隐藏层输出不相等的情况,这种策略在K=3时十分有效,因为有1个隐藏层输出不相等的情况为大多数,而有3个隐藏层输出不相等的情况很少发生。因此K=4时几何攻击效果有所下降。
同理当K=5时,有1个隐藏层输出不相等的概率约为15.6%,有3个隐藏层输出不相等的概率为约15.6%,有5个隐藏层输出不相等的概率约为3.1%。以此类推,当K不断增大时,只有1个隐藏层输出不相等的概率会越来越小,因此随着K的增大,几何攻击的效果不断下降,利用几何攻击策略的合作攻击的效果也会下降。
3.5 安全性测试算法
本节主要将合作攻击策略应用到测试K>4时方案的安全性。因为在同步过程进行到1/3后采用合作攻击策略效果最好,所以本文将时间测定算法嵌入到合作攻击中,在测试每种参数之前先测得平均同步步数,使其能够自适应参数的变化,从而保证合作攻击策略的有效性。在表4的算法2中,第(1)行的判断保证只有当同步过程进行到1/3后且当前步数为偶数步时使用合作攻击策略,否则使用几何攻击策略。第(2)~(4)行是对输出和Alice不相等的攻击者进行更新隐藏层输出,第(5)行通过投票找出票数最多的隐藏层输出表示,并让所有人都用这个表示来更新权重第(6)~(8)行。第(9)~(15)行表示采用几何策略进行更新权重。

表4 安全性测试算法(算法2)
4 性能分析
4.1 向量化方法对比
本节主要将本文方案与文献[16]所提方案进行了对比分析(详见表5)。文献[16]中主要利用了Python语言的第三方NumPy库在TPM的实现上采用向量化的计算来提高TPM之间同步的时间效率,该方法的局限性在于只有用Python语言进行编程实现时才有效。而本文主要通过定义向量化的学习规则来实现TPM的向量化,不局限于编程语言和平台,具有更强的实用性。此外,本文还给出了寻找优化参数的方法,并进行了安全性测试。
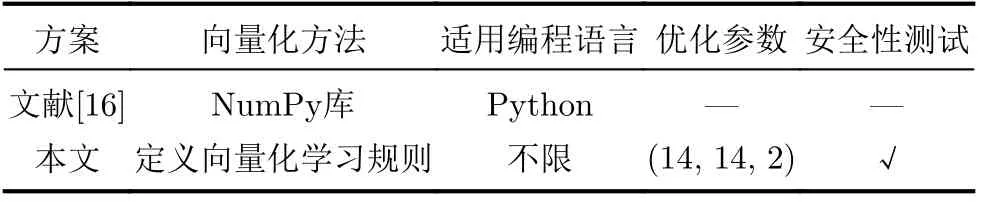
表5 向量化方法对比
4.2 仿真结果
本文采用Python语言编程实现和测试,实验环境为:Think Pad E431笔记本电脑,intel酷睿i3处理器,双核四线程,Ubuntu系统。仿真结果如表6所示,本文组合运行了1000次,主要测试了平均步数、平均时间、几何攻击成功率和合作攻击成功率。几何攻击成功概率是指单个攻击者Eve能够成功和通信双方实现同步的次数占总测试次数的百分比,合作攻击成功率是指采用100个攻击者Eve合作的方式能够成功和通信双方实现同步的次数占总测试次数的百分比。
本文的目的是寻找高效安全的参数,故不采用同步时间大于0.5 s的参数,也不对这部分参数进行攻击。从表6可看到,平均时间最少的参数为(4,64,1),仅0.0192 s。但其被合作攻击攻破的概率为99.1%,几乎完全攻破。能抵抗合作攻击的参数有6组,分别是(11,16,2),(11,16,3),(12,15,2),(12,15,3),(13,14,2)和(14,14,2)。其中(14,14,2)的平均时间是6组参数中最少的,为0.1219 s,而(11,16,3)的平均时间是6组参数中最多的,为0.4165 s,比(14,14,2)慢了0.2946 s,是(14,14,2)的3倍。
从表6可以发现,当固定L时,随着K的增大和N的减小,攻击成功率下降速度较快。图2展示了当K从8增大至14时,合作攻击成功率的下降趋势。在图2(a)中,当K的取值分别为8,9,10,11,12,13,14时,N对应的取值分别为32,29,26,24,22,20,19;在图2(b)中,K的取值分别为8,9,10,11,12,13,14时,N对应的取值分别为22,19,18,16,15,14,14。L=1时,攻击成功率下降稍缓;而L=2时,攻击成功率下降非常快,当K >10时,攻击成功率降为0。
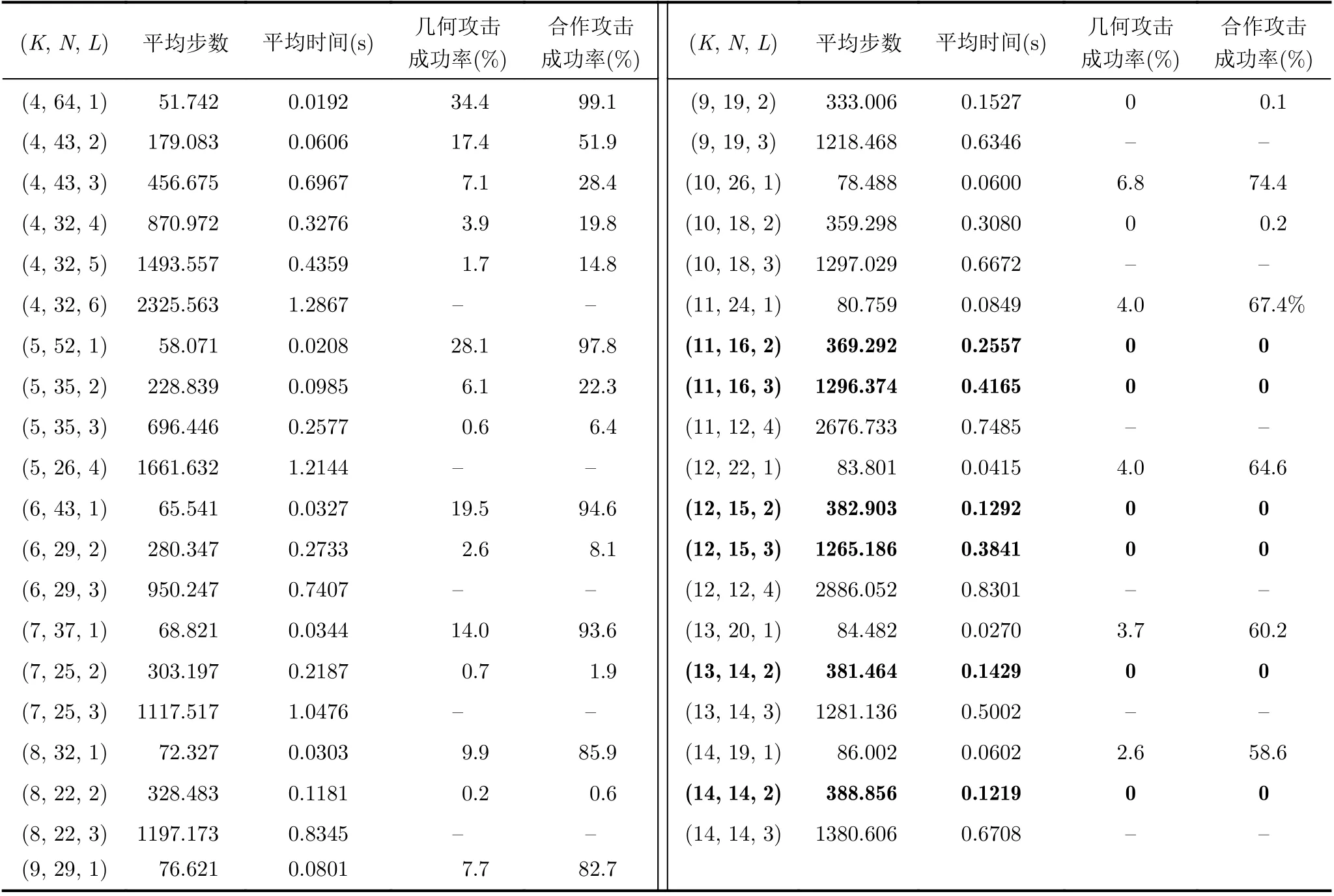
表6 仿真结果(1000次)
由于图2中K在增大而N在减小,于是本文研究了K和N单独变化对攻击成功率的影响,如图3所示。图3(a)是固定N=40和L=2,令K从4增大至14时对攻击成功率的影响,从中可以看到,随着K的增大,攻击成功率呈指数下降,直至降为0。图3(b)是固定K=4和L=2,令N从10增至40时对攻击成功率的影响,从中可以看到,随着N的增大,攻击成功率呈下降趋势。即随着N的减小,攻击成功率会增大。从图3可以得到,影响攻击成功率下降的主要因素是K,K的增大会导致攻击成功率的急剧下降直至为0。当K >14且继续增大时,由于K≤N的限制,N不得不跟着K同步增大,尽管这会进一步加强方案的安全性,但是其所需同步时间会迅速增大。所以本文得到(14,14,2)是在时间效率和抵抗已知攻击效果最好的参数。
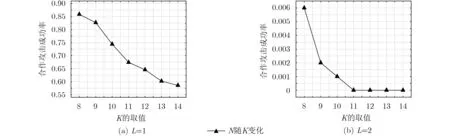
图2 K和N同时变化对攻击成功率的影响

图3 单一参数变化对攻击成功率的影响
此外,本文还研究了采用向量化学习规则对同步时间和同步步数的影响,并和没有向量化的进行了对比。同步时间的对比如图4(a)所示,向量化后的同步时间在0.01~0.04 s,比没有向量化的同步时间降低近两个数量级。同步步数的对比如图4(b)所示,二者同步所需步数基本一致,且都随着K的增大而增大。在图4中,实线表示向量化后的,虚线表示非向量化的,均固定取值N=64,L=1。

图4 向量化与非向量化的对比
4.3 效率分析
将本文的优化方案分别和文献[17,18,22]中的方案进行了效率上的对比。文献[17]中的方案是基于神经网络的密钥交换方案,所采用的参数为(8,16,23);文献[18]中的方案是基于格上LWE问题的密钥交换方案,所采用的参数为文献[18]中推荐的参数;文献[22]中的方案是基于身份的无双线性对的密钥协商方案。本文采用Pairing-Based Cryptography库对其进行了仿真实现,所采用的椭圆曲线为y2=x3+x,所采用的哈希函数为MHASH-SHA512,生成密钥长度为512 bit;本文方案采用的参数为(14,14,2)。4个方案均采用C语言实现,其余实验环境与前文一致,对每个方案进行1000次仿真,效率对比如表7所示。和基于神经网络的密钥交换方案相比,交换得到相同长度的密钥,采用向量化学习规则的本文方案完成密钥交换所需的平均时间比没有向量化的文献[17]中的方案少1/16;和基于格的方案[18]相比,由于其方案中没有提供生成512 bit长度密钥的参数,本文采用其生成256 bit长度密钥的推荐参数,其生成256 bit长度所需的平均时间比本文方案生成512 bit长度密钥所需的平均时间多1倍,且理论上文献[18]生成512 bit长度的密钥需要更多的时间。和基于身份的无双线性对的密钥协商文献[22]相比,本文方案完成密钥交换的时间远少于文献[22]。因此本文方案在时间效率上是高效和实用的。

表7 效率对比
5 结束语
本文针对神经网络学习规则串行实现效率不高的问题,给出了可并行实现的学习规则定义,对树形奇偶机进行了向量化。提出了基于树形奇偶机的密钥交换优化方案,并对可用于生成512 bit固定长度密钥的参数进行了仿真实验,主要从时间效率和安全性两个方面进行了测试。实验结果表明,本文所提密钥交换优化方案是安全高效的。采用本文所提优化方法,理论上可获得生成任意固定比特长度密钥的在时间效率和安全性上最佳的参数。在未来工作中,可以考虑使用嵌入零知识证明协议的方法进一步提高优化密钥方案的安全性,实现基于神经网络的认证密钥交换方案。
