基于改进贝叶斯非负Tikhonov正则化方法的同轴电缆信号传输畸变补偿研究

秦 风 高 原吴 双

(中国工程物理研究院应用电子学研究所 绵阳 621900)

(中国工程物理研究院复杂电磁环境科学与技术重点实验室 绵阳 621900)

1 引言

在电磁环境测试技术领域，经常采用十几米甚至几十米的同轴电缆传输测试信号，对于瞬时高频或宽带脉冲信号，经长距离同轴电缆传输时易出现畸变，且畸变程度随着信号频率、带宽以及传输距离的增大而急剧增大[1–3]。此外，当同轴电缆意外受到挤压、拉伸或折叠时，其信号传输特性会发生改变，进一步加剧信号的畸变程度，导致测试仪器记录的测量信号严重偏离实际被测信号[4–7]。为此，需对测试仪器记录的测量信号进行畸变补偿，以获得准确的被测信号，提高测试精度。

同轴电缆信号传输畸变补偿的本质是通过测试仪器记录的测量信号(即输出信号)来完成实际被测信号(输入信号)的重构；目前，主要有3类方法：衰减补偿法[8,9]、均衡网络法[10,11]和反卷积法[12,13]。衰减补偿法利用同轴电缆的衰减常数重构输入信号，方法简单、应用广泛；该方法中通常假定衰减常数与频率平方根成正比，这种近似精度有限。均衡网络法根据同轴电缆的传输特性设计补偿网络，以均衡同轴电缆对不同频率信号的衰减；而当同轴电缆改变时，补偿网络需重新设计，重复使用性低。此外，对于高频信号，补偿网络的分布参数会引入新的畸变因素，影响补偿效果。反卷积法通过同轴电缆的脉冲响应函数与输出信号的反卷积运算完成输入信号的重构，虽然计算模型能够较好呈现电缆的实际工作状态，但在计算过程中易出现病态矩阵，导致重构出的输入信号严重偏离实际信号。而在图像重建[14]和冲击力分析[15]领域，有一种应用广泛的逆问题分析方法——基于贝叶斯推理的非负Tikhonov正则化方法。该方法基于系统真实脉冲响应，在贝叶斯推断框架下进行未知输入信号的重构，使得计算模型贴近系统实际工作状态；并且，采用Tikhonov正则化方法处理不适定问题，能够有效解决病态矩阵计算过程中的不稳定问题[16,17]。该方法为同轴电缆信号补偿提供了一种新的思路，然而该方法对未知输入信号有非负限制，因而不能直接应用于补偿含有负分量的电磁信号。

因此，本文在贝叶斯推理的非负Tikhonov正则化方法的基础上，提出一种改进的信号补偿方法，本方法可完成任意值信号的分析重构，从而可应用于含有负值电磁脉冲信号的同轴电缆传输畸变补偿。在此基础上，以长度15 m的受挤压同轴电缆为对象，采用此方法完成了对双指数脉冲信号、调制方波信号、双极脉冲信号等3种不同样式脉冲信号的传输畸变补偿。结果表明：本方法补偿效果优异，相比于传统的衰减补偿法，补偿后信号与输入信号间偏差大幅减小。并且，改进的信号补偿方法具有较好的鲁棒性。

2 同轴电缆信号传输畸变补偿方法

2.1 同轴电缆信号传输畸变问题

由于同轴电缆的损耗、色散特性，输出信号往往会产生畸变，偏离于输入信号；并且随着信号频率、频带宽度以及同轴电缆长度的增加，输出信号会更加偏离输入信号。根据同轴电缆黑箱模型可知，同轴电缆的输出信号y(t)是输入信号x(t)和电缆脉冲冲击响应h(t)的卷积，即

此处，xi为输入信号离散点，yi为输出信号离散点，hi为同轴电缆脉冲响应离散点，N为信号离散点数，即采样点数。从式(2)看，当输出信号y和脉冲响应H已知时，通过矩阵直接求逆的方法得到输入信号x似乎很容易。实际上，测量数据y通常是含有噪声的，即y=H x+ω,ω为随机噪声，而矩阵H经常是病态的，导致直接求逆的方法对噪声很敏感，很小的噪声ω也会导致解出现较大的振荡，严重时会完全覆盖真实信息。因此，很难通过直接求解式(2)逆问题的方式获得准确的输入信号。

2.2 改进的基于贝叶斯推理的非负Tikhonov正则化方法

针对式(2)所示的不适定逆问题，根据经典Tikhonov正则化理论，其求解可转换为含有正则化项的最优问题

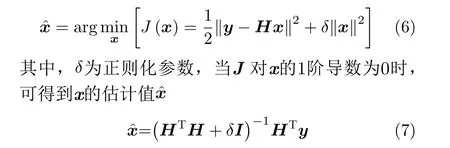
由式(6)可知，正则化参数δ的选取是求解x的关键，常用方法有广义交叉验证(Generalized Cross-Validation,GCV)法[18]、L曲线法[19]，但是在δ解值曲线过于平滑时，这些方法难以收敛。文献[20]提出了一种基于贝叶斯推断的非负正则化方法，该方法可自动选取正则化参数，同时给出逆问题的正则化解，并且求解过程的收敛性和解的唯一性得到了严格证明。但是该方法只适用于非负信号(即xi≥0)的重构分析，难以用于含有负值电磁脉冲环境信号的重构或畸变补偿；为此，本文提出一种

其中，修正后的未知输入信号n满足ni≥0。

进而可以采用基于贝叶斯推理的非负Tikhonov正则化方法来求解式(14)，得到未知输入信号n的最优估计值nˆ。根据文献[20]提出的贝叶斯统计推断方法，未知参数n的求解可转换为以下最大后验概率估计的最优化问题

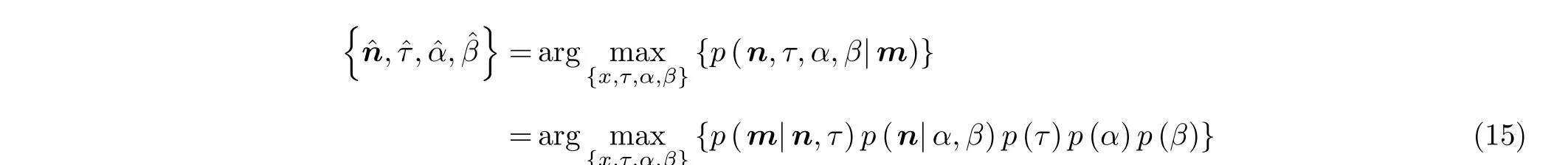
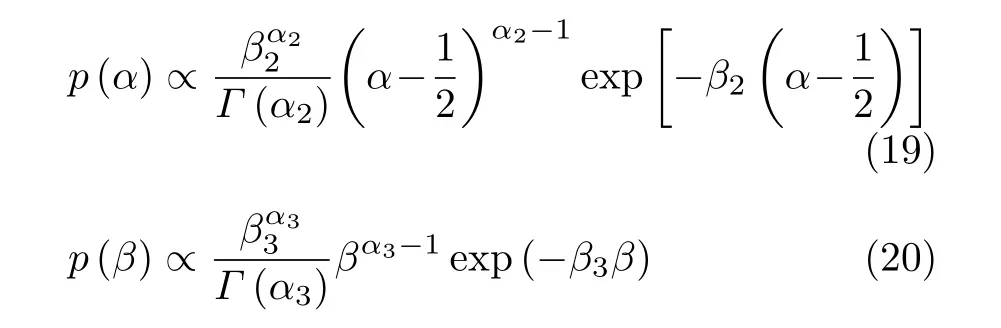
将式(16)—式(20)代入式(15)中，得到

从而将式(15)所示的最优化问题等价于求解如式(22)泛函的极小值

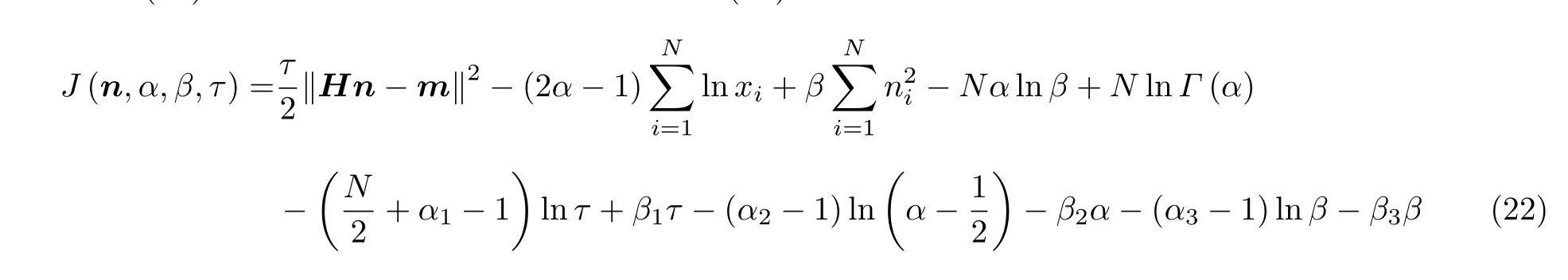
式(22)即为带非负限制的增广Tikhonov正则化泛函，而求解该泛函的极小值，相当于求解其各项偏导数为0，即ˆx即为基于改进补偿方法计算得到的输入信号估计值(即补偿信号)。

2.3 补偿效果评价方法

本文采用补偿信号或输出信号与输入信号之间的相对偏差RE来评价信号畸变补偿方法的补偿效果，具体计算方式为

3 实验与讨论

3.1 实验设置

为验证改进补偿方法的有效性和适用性，以受挤压的15 m同轴电缆为对象(图2)，开展同轴电缆传输畸变补偿实验。实验设置如图3所示，主要由任意波形发生器、功分器、0.5 m同轴电缆和受挤压的15 m同轴电缆以及数字示波器组成。其中，通过受挤压的15 m同轴电缆两个端口的信号分别为输入信号x(t)和输出信号y(t)，输入信号和输出信号由数字示波器采集得到；且为了方便，采用长度0.5 m、损耗极低的稳幅稳相同轴电缆实现受挤压的15 m同轴电缆输入信号x(t)的采集。此外，由于同轴电缆的脉冲响应难以直接测量；因此，在本文中，首先通过矢量网络分析仪测量同轴电缆的S21参数(见图4(a))，其中：测量频率范围为10 kHz～5 GHz、频率间隔为250 k Hz；然后进行快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)，获得脉冲冲击响应h(t)(图4(b))。从图4可以看出，受试同轴电缆的S21曲线抖动明显，其原因是挤压变形改变了同轴电缆的特性阻抗，从而造成了S21参数的显著变化；并且，与正常同轴电缆的脉冲冲击响应相比，受试同轴电缆的脉冲冲击响应有明显的毛刺和振荡，这将会对传输信号造成更为严重的畸变。需要注意的是，在测量输入输出信号和S21参数过程中，数字示波器、矢量网络分析仪与同轴电缆之间始终保持阻抗匹配，以消除阻抗失配对实验结果的影响。

图1 改进方法的算法流程

图2 受挤压的15 m被测同轴电缆

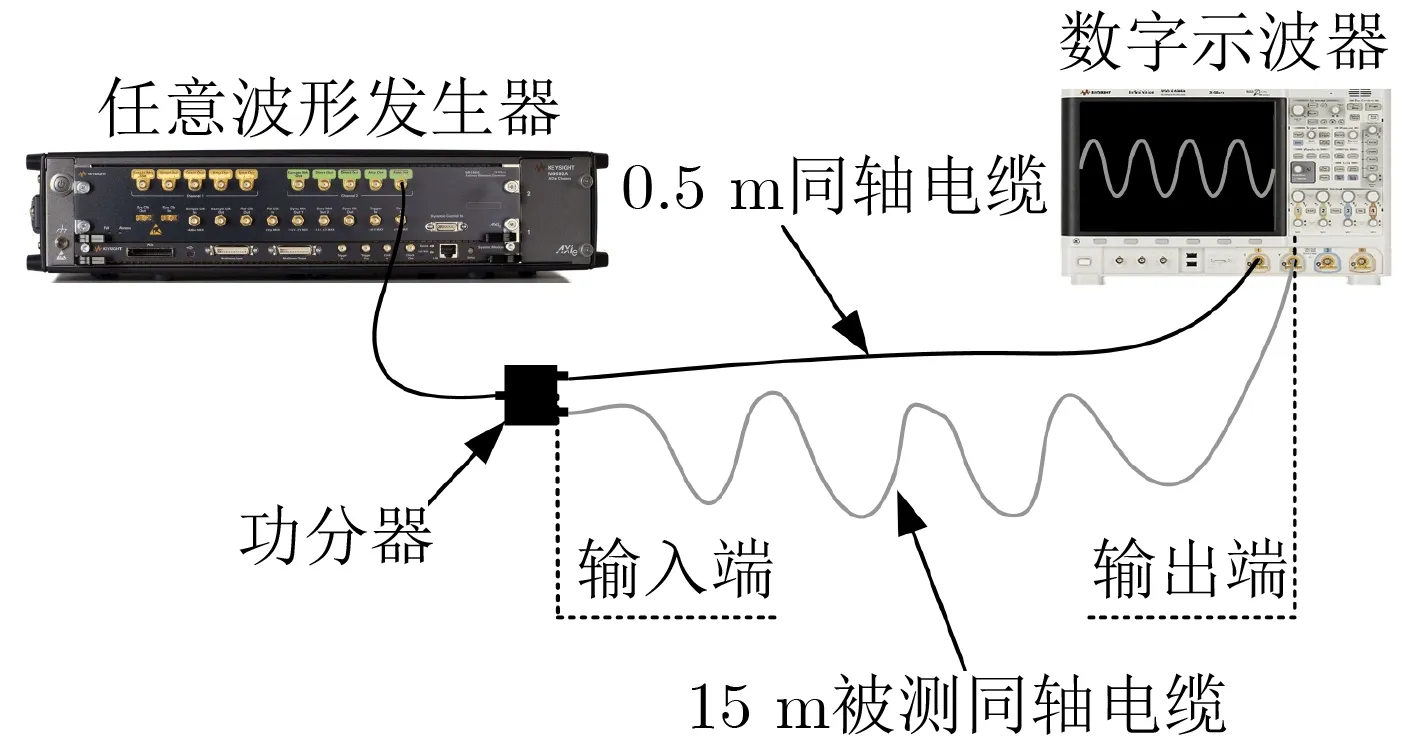
图3 实验测试设置示意图

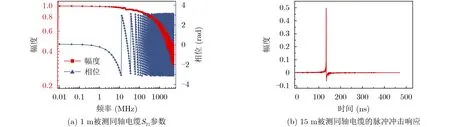
图4 同轴电缆脉冲冲击响应计算

3.2 改进补偿方法对不同类型信号的补偿

基于上述改进后的非负Tikhonov正则化方法，首先对上升时间2.5 ns、脉冲半高宽23 ns的类核电磁脉冲双指数脉冲信号(输入信号)在15 m受挤压同轴电缆中传输、畸变后的信号(输出信号)进行补偿。同轴电缆的输入信号、输出信号以及采用改进方法计算得到的补偿信号如图5所示，其中：采样时间间隔为0.2 ns，补偿过程中采用的超参数α1,α2,α3,β1,β2,β3和收敛判别参数ε分别设置为3,1,1,2×10–10,150,1×10–4和1×10–5，偏置信号d(t)采用数值为1的常量信号。15 m受挤压同轴电缆对双指数脉冲信号传输影响较大，从图5可以明显看出，输出信号与输入信号之间存在明显差异，输出信号与输入信号之间的相对偏差达到16.5%；而采用改进补偿方法补偿后的信号与输入信号吻合较好、基本一致，补偿信号与输入信号间的相对偏差仅为1.5%(表1)；表明该改进后的补偿方法能够很好地补偿输出信号。

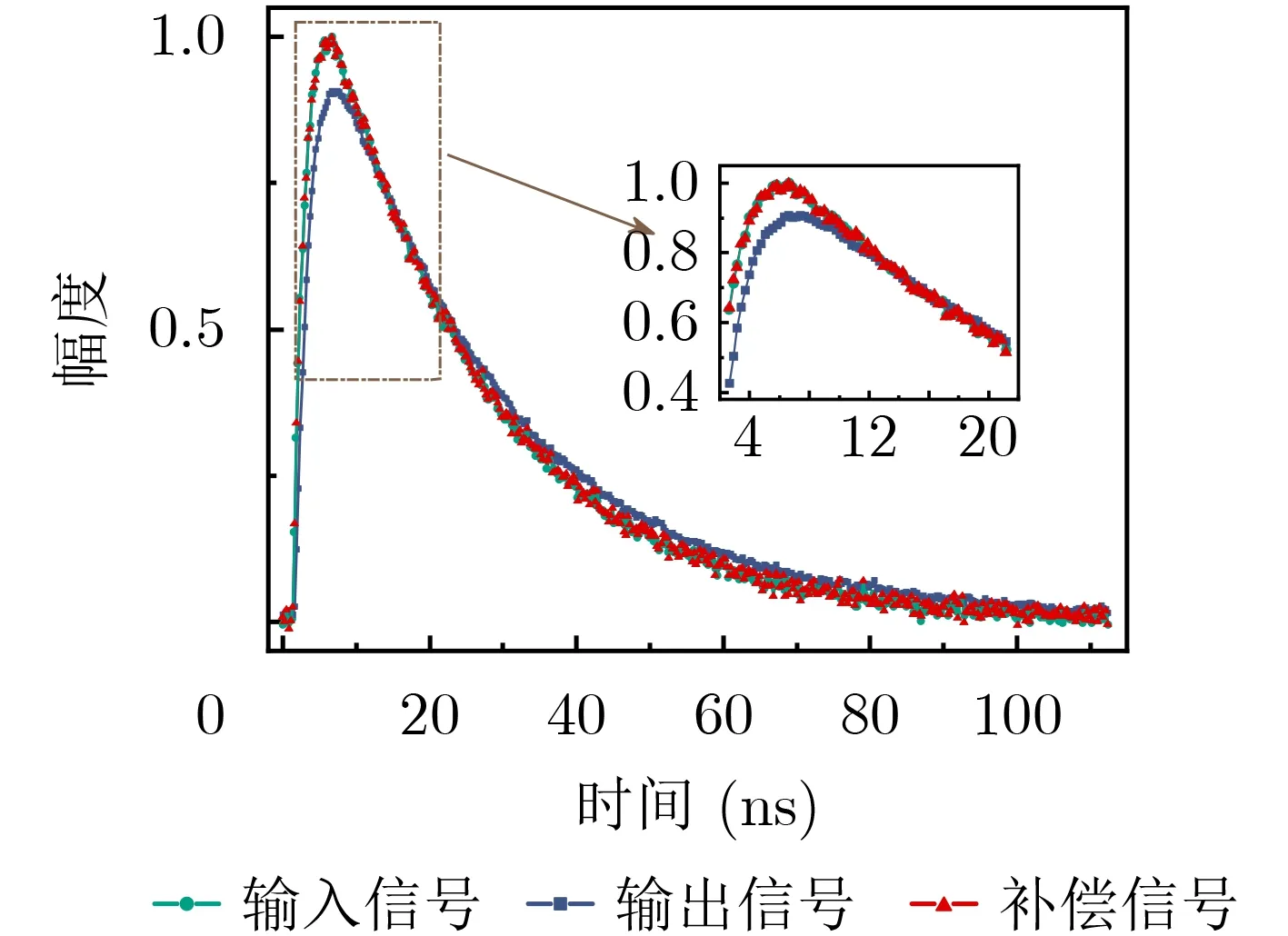
图5 双指数脉冲信号在受挤压15 m同轴电缆中的传输畸变补偿

进一步地，采用此改进后的补偿方法，分别对调制方波信号(类窄带高功率微波信号、脉宽15 ns、中心频率2 GHz、信号频率范围1940～2060 MHz)、双极脉冲信号(类宽带电磁脉冲信号、脉宽3 ns、信号频率范围33～705 MHz)经15 m受挤压同轴电缆传输后的输出信号进行补偿计算，结果分别如图6(a)、图6(b)所示；补偿过程中，调制方波信号、双极脉冲信号的采样时间间隔分别为0.025 ns,0.2 ns，所采用的超参数和收敛判别参数与上述双指数脉冲信号相同，所采用的偏置信号分别设置为数值为2.0,2.0的常量信号。从图6可以看出，对于频率较高的调制方波信号、双极脉冲信号，输出信号与输入信号之间也存在明显的差异，其相对偏差分别为24.4%,25.3%(表1)，大于频率较低的类核电磁脉冲双指数脉冲信号，更是难以直接通过输出信号准确描述输入信号。而采用改进补偿方法对输出信号进行补偿，补偿信号与输入信号几乎相同，相对偏差大幅减小(分别为2.4%,2.3%)，此实验结果进一步证实该改进补偿方法具有良好的适用性。然而，随着信号频率的增大，该改进补偿方法的补偿精度还是有稍许的下降。

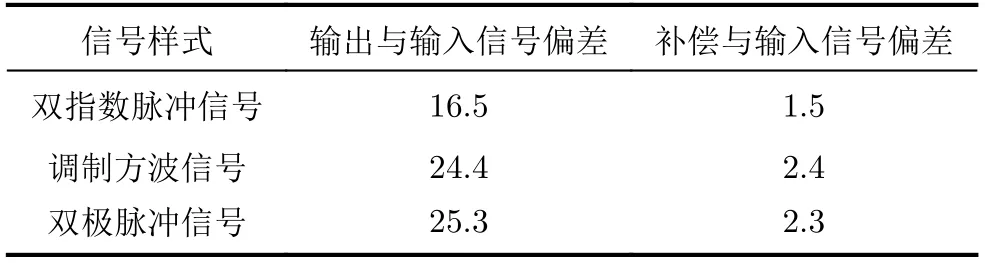
表1 输出信号、采用改进补偿方法补偿后信号与输入信号间相对偏差(%)

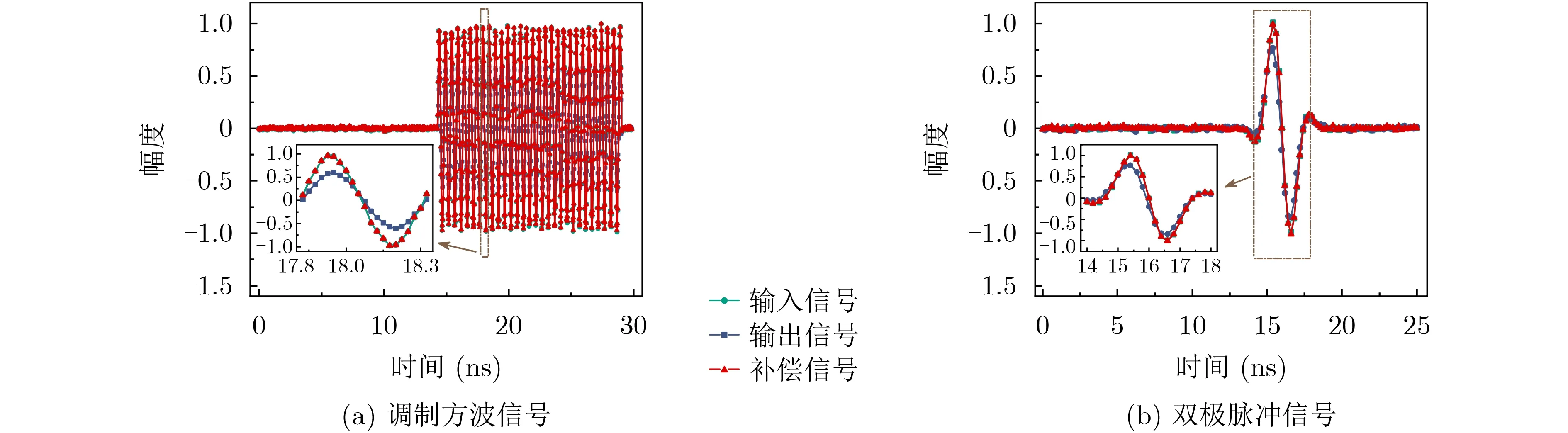
图6 改进补偿法对于不同类型信号的畸变补偿

3.3 改进补偿方法与衰减补偿法的补偿结果对比

同样地，以上述3种类型的信号作为同轴电缆的输入信号，对改进补偿方法和常用的衰减补偿法的补偿效果进行对比研究。同轴电缆的输入信号、采用改进补偿方法与衰减补偿法计算得到的补偿后信号如图7所示；从中可以看出，改进补偿方法补偿后信号与输入信号基本一致，衰减补偿法虽然也能大幅减小输出信号与输入信号的差别，但相比于改进补偿方法，补偿效果还是存在明显差距。

图7 改进补偿法与衰减补偿法的补偿效果对比

同时，针对3种不同类型的信号，还分别计算了衰减法补偿信号与输入信号、改进方法补偿信号与输入信号之间的相对偏差，结果如表2所示。当采用衰减补偿法开展信号补偿时，此3种不同类型信号的补偿信号与输入信号的相对偏差从9.0%～13.3%；相比之下，采用改进补偿法补偿后信号与输入信号的最大相对偏差不超过2.4%，远低于衰减补偿法。实验结果表明：相比于常用的衰减补偿法，提出的改进补偿方法具有更好的补偿效果。由于受试同轴电缆S21参数抖动明显，补偿过程中近似计算得到的衰减常数与实际衰减值偏差较大，进而降低了衰减补偿法补偿信号的精度；而对于改进补偿方法，在补偿过程中，未对受试同轴电缆的S21参数进行近似处理，同时还考虑了测量数据(同轴电缆输出信号)中的噪声影响，并且整个计算过程在贝叶斯非负正则化处理下稳定收敛，确保了信号畸变补偿精度。

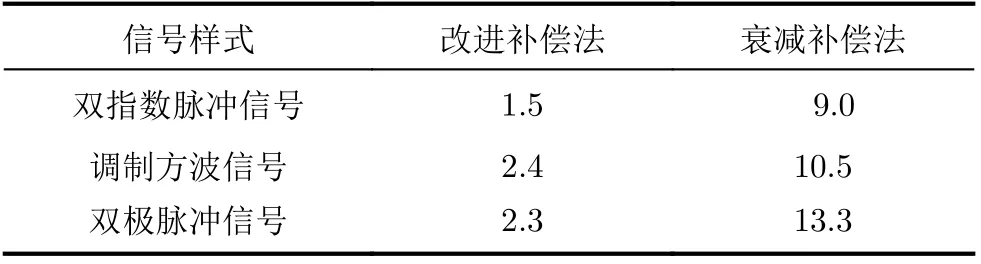
表2 不同补偿方法补偿后信号与输入信号间相对偏差(%)

3.4 不同噪声下补偿结果对比

为了研究改进补偿方法的鲁棒性，本文在3种不同输出信号y(t)中添加高斯白噪声(白噪声根据给定的信噪比(Signal Noise Ratio,SNR)随机生成)，并分别采用改进补偿方法和衰减补偿法进行信号畸变补偿计算。不同信噪比情况下，两种补偿方法补偿后信号与输入信号之间的相对偏差计算结果分别如表3、表4所示。可以看出，由于改进补偿方法在补偿过程中考虑了输出信号的噪声水平，因此在相同信噪比下，改进补偿方法的补偿效果大幅优于衰减补偿法；并且在信噪比大于30 d B时，改进补偿方法可保持良好的稳定性，表明其具有较强的鲁棒性。当信噪比小于30 d B时，由于输出信号受噪声影响较大，测量的信号质量明显下降，导致补偿精度随之降低。

表3 不同信噪比下改进补偿方法补偿后信号与输入信号间相对偏差(%)

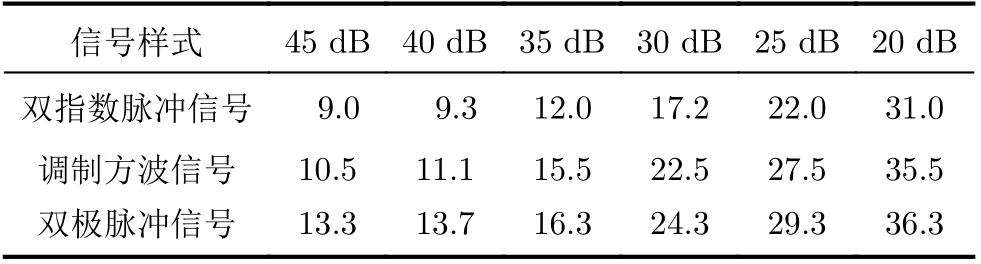
表4 不同信噪比下衰减补偿法补偿后信号与输入信号间相对偏差(%)

4 结束语

本文针对同轴电缆信号传输畸变问题，基于贝叶斯推理的非负Tikhonov正则化方法，提出一种改进的同轴电缆信号传输畸变补偿方法。并以受挤压的15 m同轴电缆为对象，完成了3种不同类型信号的同轴电缆传输畸变补偿实验，并将改进方法的补偿结果与传统衰减补偿法的补偿结果进行了比对。结果表明，改进补偿方法具有优异的补偿效果、较强的鲁棒性及良好的普适性。所提改进补偿方法仅需利用系统的脉冲响应函数，整个计算过程无特别限制，本方法可推广应用于其他系统(如天线、滤波器等)的信号传输畸变补偿或输入信号重构。