巷道变形差异化响应特征及支护设计分析
2021-08-26郑建伟鞠文君孙晓冬李文洲周逸群褚晓威赵凯凯
郑建伟,鞠文君,孙晓冬,李文洲,周逸群,褚晓威,刘 彪,赵凯凯
( 1. 煤炭科学研究总院 开采研究分院,北京 100013;2. 中煤科工开采研究院有限公司,北京 100013;3. 天地科技股份有限公司 开采设计事业部,北京 100013;4. 陕煤集团铜川矿业有限公司,陕西 铜川 727101 )
我国每年仅新掘进的井工巷道长度就超过12 000 km[1-2],且随着开采水平的不断延伸,巷道所处的地质环境和应力环境的复杂程度不断增加,因此巷道围岩的稳定性问题成为我国煤炭资源实现安全开采所必须面对的主要问题之一。巷道出现的变形是其围岩煤岩体对所处应力环境最直观的响应形式,可以认为巷道变形的响应特征与所处的应力环境( 外部因素 )和围岩煤岩体自身的力学行为( 内部因素 )有直接的关系[3-4]。大量学者基于连续介质力学对巷道围岩进行分析,提出了如关键承载圈力学模型[5]、松动圈模型[6]、巷道蝶形塑性区模 型[7]、等效断面模型[8]等力学模型,也有学者将不同断面形状巷道简化为圆形、椭圆等形状,并借助 复变函数等数学方法对围岩的应力分布进行研 究[9-10],结合上述力学模型来揭示巷道变形的外在因素;随着研究的深入,巷道围岩煤岩体的复杂力学行为特征逐步受到重视,因此在上述力学模型中进一步考虑到煤岩体的“弹-脆-塑”性能[11]、流变效应[12]、应变软化效应[13]等,内外因素的综合考虑对于巷道的变形刻画在理论层面上得到了显著发展。
在现场实际生产过程中,不同应力环境下巷道顶底板和两帮的变形程度不同,呈现出典型的差异化响应特征。如上所述,诸多学者从应力角度、材料属性角度对巷道的整体变形展开深入研究,但是针对巷道变形差异化响应特征尚未进行深入研究,同时经典的轴变论对巷道最终变形特征进行分析,但是对于巷道变形差异化响应过程并未进行详细的论述。基于此,本文借助弹性力学建立不同应力条件下考虑支护压力的圆形巷道力学模型,分析得到了巷道变形差异化响应特征与外部应力条件的内在对应关系,且结合上述分析确定了山西某矿152052巷道支护设计方案,同时也可以为类似地质条件下巷道支护设计提供一定的理论依据。
1 巷道围岩力学分析
1.1 巷道围岩力学模型建立
首先对巷道及其围岩进行理想化处理(① 忽略其自重影响;② 认为围岩煤岩体符合弹性力学的基本假设 ),将巷道简化为圆形,在弹性力学的基础上建立不同应力条件下考虑支护压力的圆形巷道力学模型,如图1所示。依据弹性力学中的叠加原理可知,可以将考虑巷道支护压力和双向不等压条件下巷道及其围岩的受力状态Ⅰ( Ⅰ型受力状态 )分解为单纯考虑支护压力的巷道及其围岩的受力状态Ⅱ( Ⅱ型受力状态 )和仅考虑双向不等压条件下巷道及其围岩的受力状态Ⅲ( Ⅲ型受力状态 ),图1中σr,σr1,σr2分别表示Ⅰ型、Ⅱ型和Ⅲ型受力状态下巷道围岩煤岩体所承受的径向应力;σθ,σθ1,σθ2分别表示Ⅰ型、Ⅱ型和Ⅲ型受力状态下巷道围岩煤岩体所承受的切向应力;R为巷道的半径;r和θ分别为所研究的微单元距巷道中心的距离和坐标角;Pv,Ph分别为巷道及其围岩煤岩体所承受的垂直应力和水平应力;Pi为人为支护对于巷道表面形成的支护压力。
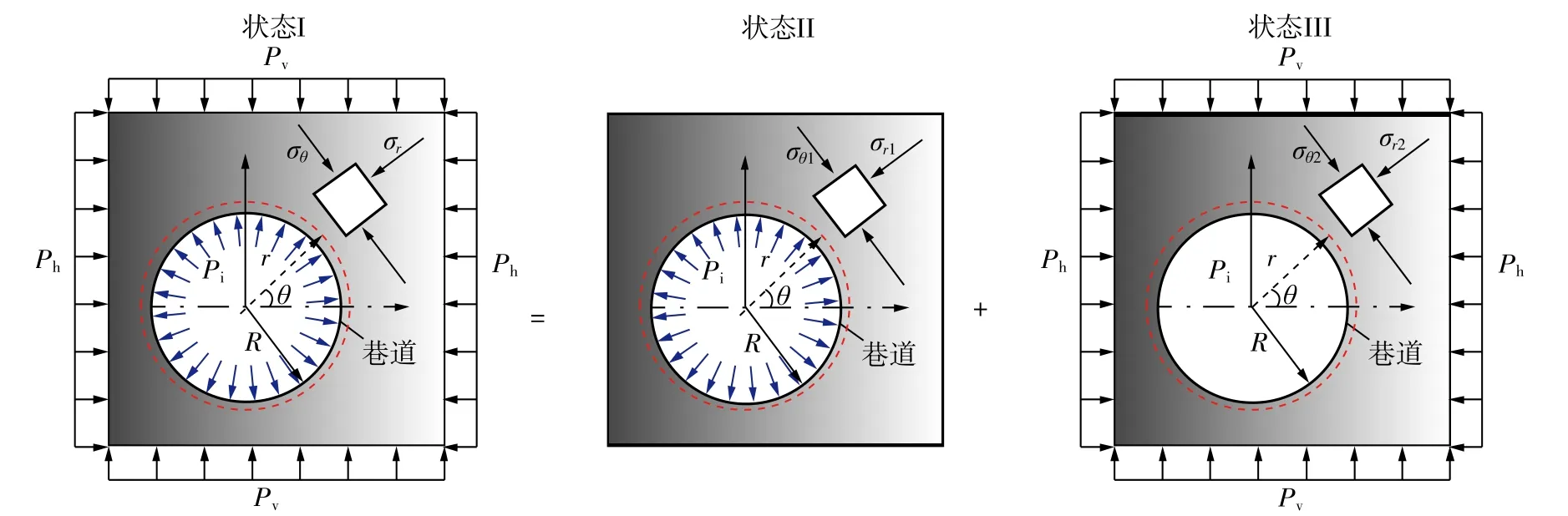
图1 巷道围岩力学模型 Fig.1 Mechanical model of roadway surrounding rockmass
由文献[14]可知,巷道及其围岩的Ⅰ型受力状态中巷道围岩煤岩体内各点的切向应力和径向应力的表达式为
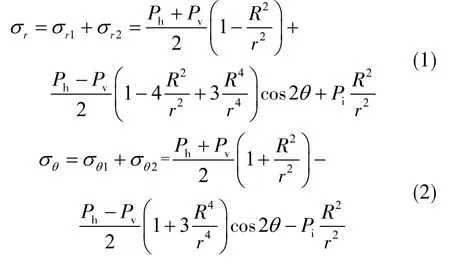
Ⅰ型受力状态中巷道围岩煤岩体的变形协调方程和应力-应变方程分别如式( 3 ),( 4 )所示,联立式( 3 ),( 4 ),可以得到Ⅰ型受力状态中巷道围岩煤岩体的径向位移的表达方程如式( 5 )所示,其中,υ和E分别代表巷道围岩煤岩体的泊松比和弹性模量,εθ代表巷道围岩煤岩体的切向应变,u代表巷道围岩的径向位移。

联立式( 1 ),( 2 )和( 5 ),可得Ⅰ型受力状态中巷道围岩煤岩体的径向位移的完整表达方程,即

化简式( 6 ),得到Ⅰ型受力状态中巷道围岩煤岩体的径向位移的简化表达式为
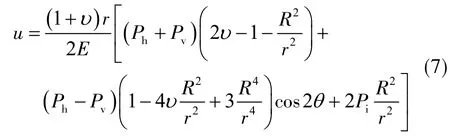
1.2 巷道围岩变形差异化响应特征分析
借助上述得到的巷道径向位移表达方程( 式( 7 ) ),分析巷道边界上的径向位移,即R=r,令Ph=kPv,其中,k表示水平应力和垂直应力的比值,即侧向应力系数,改写式( 7 )得到

现主要分析圆形巷道与坐标轴在第1象限的交点,即将θ=0和θ=π/2分别代入式( 8 ),得
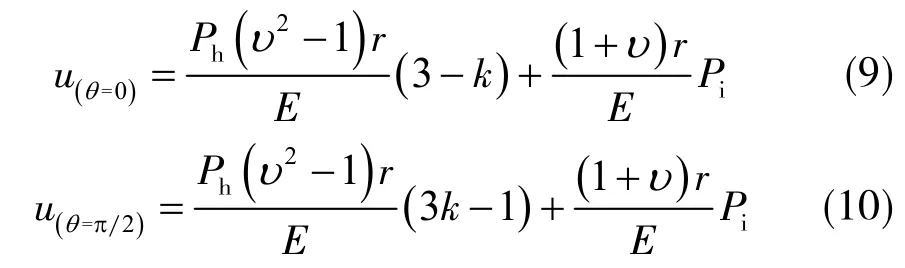
结合煤岩体岩石物理力学特性可知0<υ<0.5,由式( 9 ),( 10 )可知巷道整体变形量随着k的增加而增加,随着iP的增加而降低;且在不同应力因子k的影响下,结合式( 1 ),( 2 )可知巷道呈现出明显的变形差异化响应特征:当0<k<1/3时,巷道顶底板在拉应力作用下位移背离巷道圆心发展,两帮在压应力作用下位移向巷道圆心发展,两帮位移量大于顶底板的位移量,如图2( a )所示;当1/3<k<1时,巷道顶底板和两帮均受压应力作用,巷道表面位移均向巷道圆心发展,两帮位移量大于顶底板位移量,如图2( b )所示;当1<k<3时,巷道顶底板和两帮均受压应力作用,巷道表面位移均向巷道圆心发展,两帮位移量小于顶底板位移量,如图2( c )所示;当3<k时,巷道顶底板在压应力的作用下位移向巷道圆心发展,巷道两帮在拉应力的作用下位移背离巷道圆心 发展,两帮位移量小于顶底板位移量,如图2( d )所示。

图2 不同k值条件下巷道断面位移演变特征 Fig. 2 Roadway displacement evolution under different stress ratio k
1.3 巷道围岩变形差异化响应过程分析
经典的“轴变论”认为巷道在外部应力环境中,其围岩煤岩体经过一系列的自组织调整( 局部破坏诱发其他部位破坏 )后会形成具有一定轴比的“( 类 )椭圆”形几何断面,且具有良好的稳定性。这一理论在大量的现场实践和实验室试验分析中得到验证且被广泛接受,已有的研究分析均直接给出了巷道由最初态( 圆形 )到最终稳定形态( 椭圆 )的描述,缺乏对于最初态到最终稳定态过程的刻画和分析。
上述1.1节和1.2节内容对巷道围岩在不同k条件下所呈现出的变形差异化响应特征进行分析,对比图2( a ),( d )可知:巷道在相对较小应力方向的变形量较大,且均受压应力的作用而变形量朝巷道中心发展;当0<k<1/3和3<k条件下,巷道在较大应力方向受拉应力作用,该方向的变形量背离巷道中心发展;当1/3<k<1和1<k<3条件下,巷道在较大应力方向受压应力作用,该方向的变形量朝巷道中心发展。整体来看图2所示的巷道呈现出的差异化响 应特征与轴变论所强调的巷道自稳之后的最终边界形态有很好的对应关系,从而一方面证明了本 推论的合理性,一方面对轴变论中巷道边界的演 化过程进行了补充,进一步丰富轴变论的理论内涵。
2 基于巷道变形差异化响应特征的支护设计启发
上述力学分析是基于弹性力学开展的,考虑到实际现场工程所面对围岩煤岩体的复杂物理力学特性,如需具体应用到现场工程实践当中,需要再次深入挖掘上述力学模型所蕴含的具有适用性的科学内涵。进一步分析图2可知:假设巷道围岩的顶底板和两帮的物理力学特性一致,巷道因开挖和应力的重新分布就会导致其顶底板和两帮出现不同的变形响应特征,当顶底板和两帮煤岩体物理力学属性不同时,则巷道变形响应的差异化程度就会相应地发生变化。通常情况下巷道顶底板煤岩体的力学特性要强于两帮煤体的力学特性,即顶底板通常具有更高的极限承载能力,此时,如果巷道垂直应力大于水平应力时(k<1 ),则巷道两帮的变形量会明显高于巷道顶底板的变形量;如果巷道两帮煤体的极限强度高于顶底板煤岩体的极限强度,且巷道垂直应力小于水平应力时(k>1 ),则巷道顶底板的变形量会明显高于巷道两帮的变形量。基于此,上述模型可以将巷道围岩煤岩体物理力学特性和所处的应力环境更好地结合起来,对巷道顶底板和两帮变形差异化响应特征的力学内涵等进行解释。人为支护的目的是通过及时对巷道进行支护来达到控制巷道围岩变形量的目的,避免巷道顶底板或者两帮出现较大的差异变形,从而导致围岩应力不均匀程度增加,进一步恶化巷道围岩煤岩体的承载能力。因此基于上述巷道围岩力学模型分析,既可以解释巷道顶底板变形量与两帮变形量差异化的内在原因,同时也可以对相应支护的设计提供一定的启发。
( 1 ) 当巷道处在水平应力大于垂直应力的情况下( 1≤k),巷道顶底板的变形量大于两帮的变形量,此时需要重视对于巷道顶( 底 )板的支护,通过提高顶( 底 )板的支护强度来控制巷道变形量;当巷道处在水平应力小于垂直应力的情况下( 0<k<1 ),巷道两帮的变形量大于顶底板的变形量,因此需要重视对于巷道两帮的支护;如上所述的重视两帮支护并不是指可以忽略或者降低顶( 底 )板的支护强度,而是指在保障顶( 底 )板的支护强度的基础上,适当的采取有效的支护设计( 参数 )来提高两帮的支护强度,具体的可以针对不同的应力条件,在需要进行重点支护的两帮增设锚索、调整锚杆长度以及锚固方式、选用更高力学性能的锚杆、局部注浆、优化间排距、提高预紧力、增设钢护板等护表构件等措施,通过上述措施来更好地控制两帮的变形量,从而在一定程度上促进巷道两帮和顶底板实现均匀变形;反之如果需要对顶( 底 )板进行重点支护,同样可以采取上述措施来达到控制巷道顶( 底 )板变形量的目的,且可以依据特定情况来判断是否对底板进行支护,如底板岩层强度低且易变形时则需要对底板进行支护,如果底板条件较好则可以简化或者取消对底板的支护。
( 2 ) 在具体的实践过程中,针对沿空留巷、小煤柱巷道等侧向临空巷道进行支护时,因为临近采空区,则可以认为作用在巷道帮部的水平应力的等级发生了一定的降低,假设作用在巷道的垂直应力不变,由上述巷道力学模型分析结果( 图2 )可知两帮的变形量要大于此类条件下顶底板的变形量,因此针对此类特殊巷道要重视对于两帮的支护;当巷道处于回采工作面超前支承应力影响范围内时,可以认为巷道围岩所承受的垂直应力增大,假设作用在巷道围岩上的水平应力保持不变,则同样由上述巷道力学模型分析可以给出在超前支承应力影响范围内巷道整体变形量增加且两帮变形量要大于顶底板变形量的内在力学解释,针对超前支承应力影响范围内的巷道在对顶板提供必要的支撑的前提下,也应该对巷道两帮进行支护;针对上覆采空区范围下的巷道,由于上覆采空区的形成可以认为垂直应力得到一定的释放,从而降低了垂直应力的等级,假设在水平应力不变的情况下,此类巷道的顶底板更容易发生变形,因此要重视对于巷道顶( 底 )板的支护,来减小巷道顶( 底 )板的变形量。
( 3 ) 文献[15-16]表明在无特殊地质构造影响条件下,垂直应力随着测量位置深度的增加总体上呈线性增加,水平应力随着测量位置深度的增加具有增大的趋势( 离散性显著 ),在埋深较浅的地层内地应力的类型为σH>σh>σV,因此处于浅埋条件的巷道所承受的水平应力为最大主应力,此时顶底板变形量较大,要重视对于巷道顶( 底 )板的支护;随着巷道埋深增加,地层内地应力的类型则会改变为σV>σH>σh,巷道所承受的垂直应力会逐渐转变为最大主应力,在此过程中就需要逐步重视对于巷道两帮的支护。
3 基于巷道变形差异化响应特征的支护设计实例
3.1 工程背景
以山西某煤矿15205工作面回风巷道( 152052巷道 )为研究对象,该巷道埋深范围为469~559 m,设计掘进断面宽5.0 m,高4.5 m,且沿15号煤层顶板进行掘进,煤层平均厚度4.9 m,煤层倾角0°~6°,掘进煤层结构简单稳定。152052巷道东南方向为15203工作面的采空区,15203工作面回采已完成且覆岩结构已经稳定( 回采结束12个月以上 ),两工作面间煤柱宽度为15.0 m,15205回采工作面与相邻工作面空间关系如图3所示。152052巷道顶板以上0~1.3 m为泥质胶结的砂质泥岩,1.3~8.1 m为钙质胶结的细砂岩,8.1~10.0 m为较完整粉砂质泥岩,巷道两帮均为煤体且完整性较好;底板0~1.8 m为呈块状构造的铝土质泥岩,1.8~5.2 m为呈块状构造的泥岩,152052巷道岩层柱状信息如图4所示。为了获取152052巷道附近地应力信息在相邻巷道布置地应力测站,测试结果见表1,分析可知研究巷道所在区域应力场类型为典型的σH>σV>σh型应力场,最大水平主应力与研究巷道的夹角为71°54′30″。

图3 152052巷道位置及与相邻工作面空间关系 Fig. 3 Relative position between 152052 roadway and adjacent mining face

图4 152052巷道岩( 煤 )层柱状信息 Fig. 4 Geology columnar map of 152052 roadway

表1 原岩应力测试结果 Table 1 Results of in-situ rock mass stress
3.2 巷道围岩应力及内部裂隙分析
基于上述巷道围岩变形差异化响应特征分析,通过坐标转化公式?[17]可知作用在152052巷道上的垂直于巷道轴线的水平应力(σx)、平行于巷道轴线的水平应力(σy)和垂直应力(σz)分别为8.44,13.74,12.98 MPa,则真实作用在152052巷道围岩煤岩体上的垂直应力大于其水平应力(k=Pv/Ph=1.54 ),且该巷道的受力特征符合图2( c )所描述的情况。152052巷道两帮的变形量会大于顶底板的变形量,与现场巷道出现的变形特征相符,究其原因可以认为两帮煤体的力学性能弱于巷道顶底板岩层的力学性能,且在如上所述的应力环境中会进一步加剧巷道两帮煤体内部裂隙的发育程度,与顶底板岩体相比,两帮煤体内部裂隙的形成和高度发育导致了巷道两帮变形量明显大于顶板变形量。因此对152052巷道顶板和两帮开展钻孔窥视探测,窥视结果如图5所示,探测结果显示152052巷道顶板整体完整性相对较好,裂隙分布均匀且相对较少;煤柱侧煤体0.1~0.7 m内裂隙相对发育,0.8~1.5 m内纵向裂隙相对发育,局部出现轻微破碎现象;煤壁侧煤体内部存在较为明显的纵向裂隙,整体上裂隙分布均匀且发育,同时存在局部破碎现象。由上述巷道顶板及两帮围岩内部裂隙发育情况探测可知,152052巷道两帮煤体内部裂隙发育程度要高于顶板裂隙发育程度,所以巷道两帮变形量要大于顶板变形量,同上述力学模型分析结果基本一致。

图5 152052巷道围岩内部裂隙探测结果 Fig. 5 Borehole optical observation in roof and coal seam side of 152052 roadway
3.3 巷道支护设计
通过上述152052巷道所处应力环境分析得到的巷道围岩顶( 底 )板及两帮的变形量特征,结合围岩内部裂隙发育特征,可知巷道两帮变形量要大于顶板变形量,因此要重视对于巷道两帮的支护强度。综合相邻巷道的支护实践以及上述巷道差异性响应特征分析结果,在相邻巷道支护设计的基 础上对其进行有针对性的调整,最终确定采用“锚杆+锚索+金属网+钢筋托梁”的形式对152052巷道进行支护,其中尤其注重巷道帮部的支护,在巷道帮部增设锚索来控制帮部围岩的变形,152052巷道顶板及两帮支护参数及设计分别如图6和表2所示。
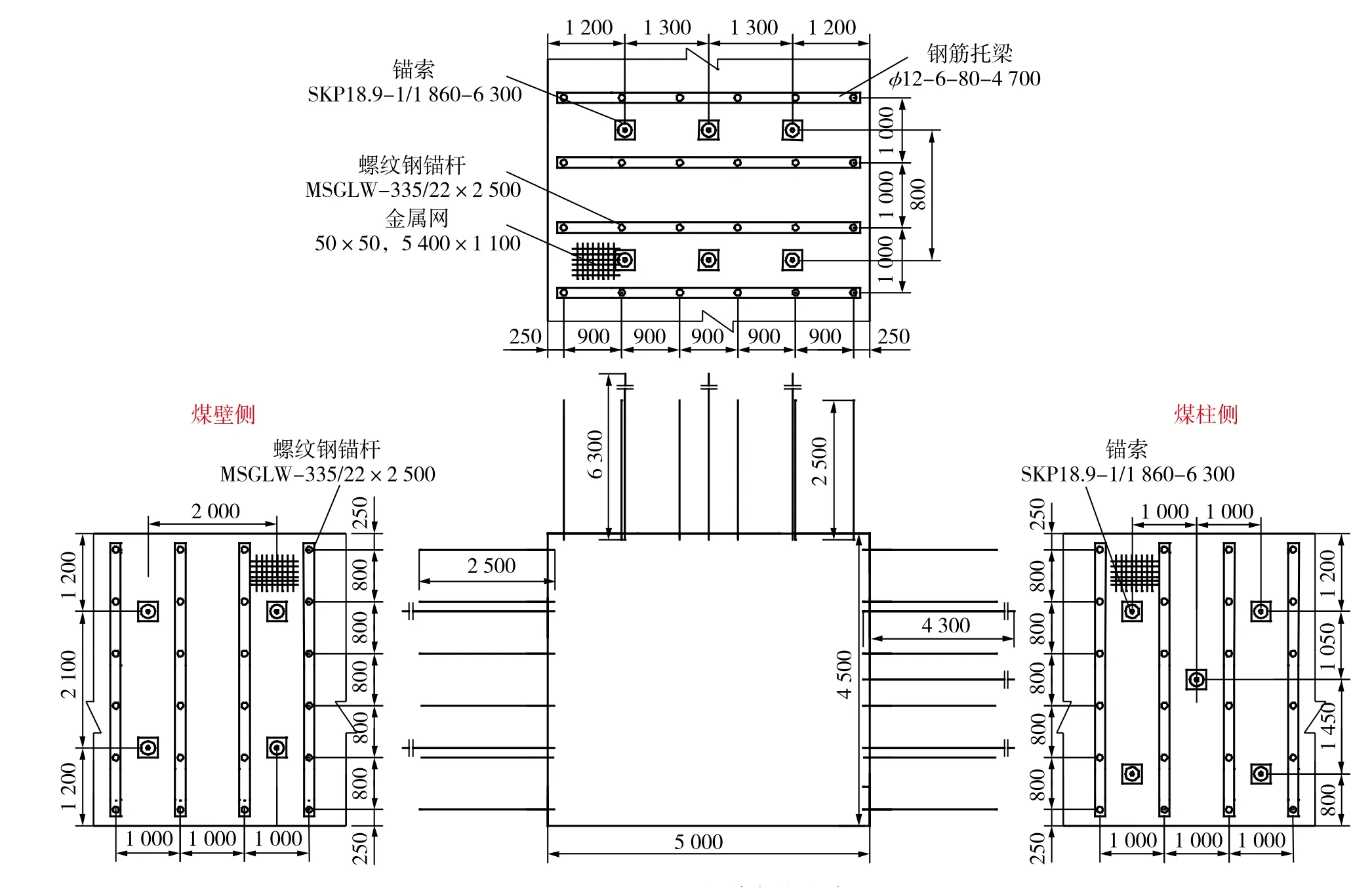
图6 152052巷道支护设计 Fig. 6 Supporting design of 152052 roadway
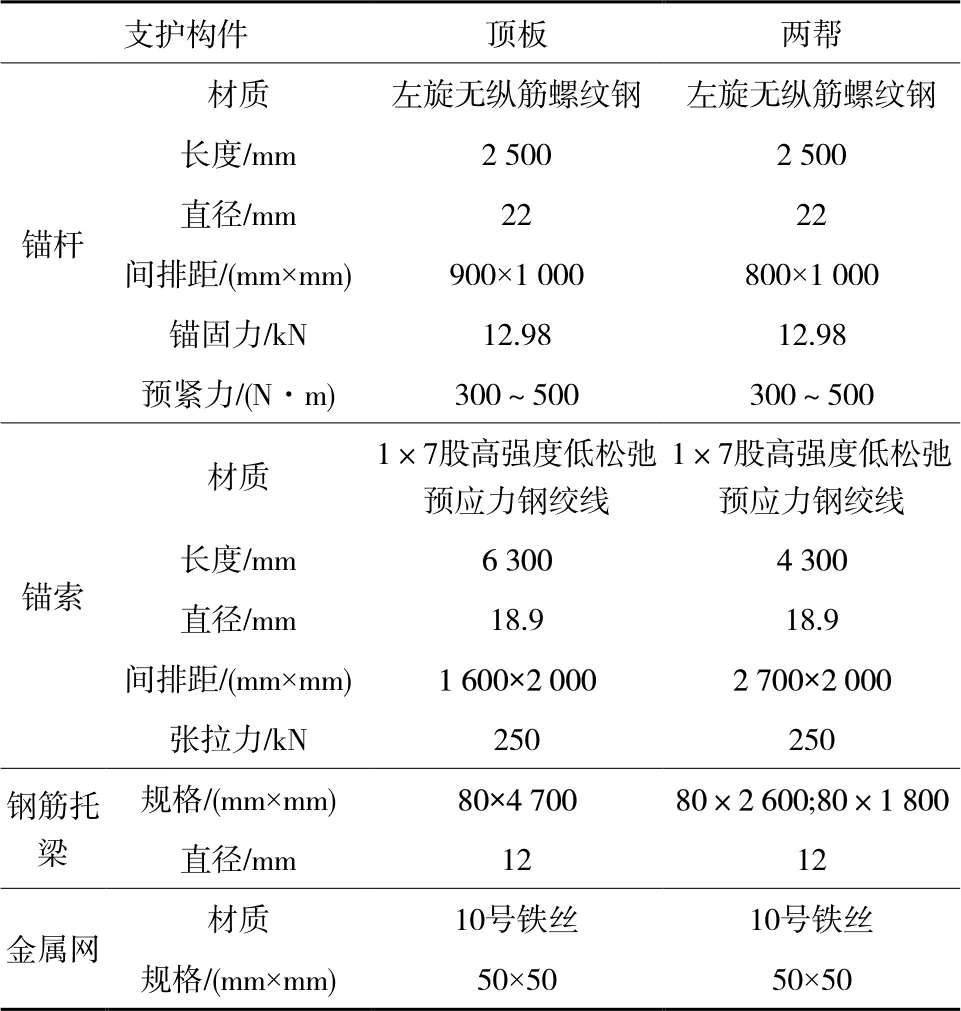
表2 152052巷道支护设计参数 Table 2 Supporting design of 152052 roadway
为了对支护效果进行检测,在152052巷道布置断面变形测站,监测152052巷道在掘进过程中巷道变形量,监测结果表明在掘进过程中巷道顶底板变形量最大达到233 mm,巷道两帮变形量达到565 mm,其中煤壁侧最大变形量达到328 mm,煤柱侧最大变形量达到237 mm。整体来说152052巷道顶底板和两帮的变形量得到有效控制,掘进完成后巷道的断面变形量整体不大,巷道断面的成形较好,尤其与相邻的152032巷道的变形量( 顶底板变形量最大达到605 mm,两帮变形量达到2 135 mm )相比更是显著降低,说明本设计对于巷道围岩煤岩体支护取得良好的效果。
4 结 论
( 1 ) 基于弹性力学理论建立了不同应力条件下考虑了支护压力的圆形巷道力学模型,认为巷道整体变形量随着k的增加而增加,随着Pi的增加而降低,且巷道变形差异化响应特征为:当0<k<1时,两帮位移量大于顶底板的位移量;当1<k时,两帮位移量小于顶底板位移量。
( 2 ) 结合巷道变形差异化响应特征可以为支护设计提供以下三方面的启发:① 当1<k,需要重视对于巷道顶( 底 )板的支护,当0<k<1,需要重视对于巷道两帮的支护;② 针对沿空留巷、小煤柱巷道等侧向临空巷道、回采工作面超前支承应力影响范围内的巷道要重视对于两帮的支护,针对上覆采空区范围下的巷道,要重视巷道顶( 底 )板的支护;③ 一般情况,浅埋巷道要重视对于顶( 底 )板的支护,深部巷道要重视对两帮的支护。
( 3 ) 通过在山西某煤矿152052巷道布置地应力测站得到作用在152052巷道上的应力信息,借助钻孔窥视分析巷道围岩内部裂隙发育特征,确定重视巷道两帮的支护对策,并提出了采用“锚索+锚杆+托板+金属网”的支护设计,且取得了良好的支护效果。
