适用倾斜滑面的刚性抗滑桩最小嵌固深度计算方法
2021-08-26肖世国孙来宾
肖世国,齐 远,孙来宾
(1.西南交通大学高速铁路线路工程教育部重点实验室,四川 成都 610031;2.西南交通大学地质工程系,四川 成都 610031)
0 引言
抗滑桩将桩体受荷段后侧滑坡推力通过嵌固段传递到滑面以下稳定地层,在嵌固段周围岩土体中产生作用力,当该侧向作用力小于嵌固段地层侧向抗力时,嵌固段地层处于稳定状态[1−4]。因此,嵌固段地层的侧向抗力是决定抗滑桩能否有效加固坡体的一个重要因素。
实际上,桩体嵌固段深度对抗滑桩侧向承载性能有重要的影响[5−6],有学者曾对这一问题进行研究。吴坤铭等[7]建立了嵌固深度的可靠性分析模型,基于强度折减有限元法进行了可靠度分析,建议在确定抗滑桩嵌固深度时应考虑相关参数变异的影响。胡晓军等[8]认为地层侧向应力的容许值应符合摩尔—库仑强度准则,抗滑桩嵌固深度选取应考虑边坡工程等级。于洋等[9]针对双排抗滑桩施工过程中前、后排抗滑桩嵌固深度的选取问题,基于FLAC3D程序,建立简化的双排抗滑桩数值计算模型,研究了前、后排桩嵌固深度变化时抗滑桩侧向位移、弯矩、剪力和抗滑力的变化规律。张文居等[10]基于抗滑桩嵌固深度确定一般原则,针对不同地层及不同的地基系数形式,建立了嵌固深度可靠性设计的数学模型。肖尊群等[11]根据抗滑桩滑面以下桩侧压应力在两个深度处的极值,分别建立两个极值下刚性抗滑桩嵌固深度可靠性分析的功能函数,给出了模糊随机可靠性分析模型。蒋建国等[12]根据刚性抗滑桩的侧压应力应小于桩周土极限抗压强度这一基本原则,对刚性抗滑桩的嵌固深度进行了分析,得出了嵌固深度的简化公式。
文献[13]则建议,对于嵌固段地层为土层或严重风化破碎岩层的抗滑桩,当滑面水平或较为平缓时,须满足式(1)以确定其嵌固深度。
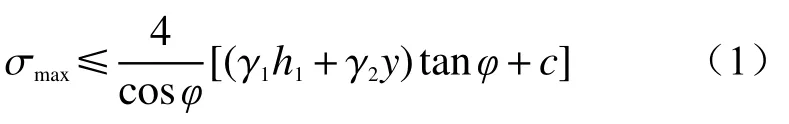
式中:σmax——嵌固段桩侧最大压应力;
γ1、γ2——受荷段、嵌固段土体的重度;
φ、c——嵌固段土体的内摩擦角、黏聚力;
h1——受荷段长度;
y——嵌固段计算点距滑面的深度。
而当滑面倾角β 较大且β≤φ0(φ0为滑床的综合内摩擦角)时,滑床中任意深度y处横向承载力计算式为:

以往这些研究多数针对桩前滑面水平或近水平的情况。实际上,当桩前滑面为明显倾斜形态时,其嵌固段深度的确定则不能仍简单采用水平滑面时的方法。尽管个别规范[13]对滑面倾斜时也有建议算法,但相关方法经验性较强,缺乏较充分的理论依据。马显春等[14]基于相似原理,进行抗滑桩加固陡倾滑面滑坡的物理模型试验,研究了3 种不同嵌固深度的抗滑桩嵌固段受力状态和桩前滑床破坏特征,给出了倾斜滑面时抗滑桩嵌固深度的试验参考值,但对此问题的理论研究相对较少。
有鉴于此,本文针对桩前为倾斜滑面且桩体嵌固段地层为土质或类土质地层的刚性抗滑桩加固边坡或滑坡问题,基于地基系数法中倾斜地面条件下的“m”法(m为地基侧向抗力系数的比例系数),得到抗滑桩嵌固段不同深度处桩侧压应力,再采用塑性极限分析方法,得到嵌固段土体极限抗力,根据桩侧地层设计压应力不大于地层极限承载力的原则,确定滑面倾斜条件下抗滑桩的最小嵌固深度。
1 分析方法
假设桩体为刚性桩,即不考虑嵌固段桩体挠曲变形影响。在滑坡推力作用下,桩体嵌固段绕其上某一点C 转动,基于刚性挡墙被动土压力分析的土体破坏模式[15],对于嵌固于土质或类土质地层的抗滑桩,可对嵌固段前侧土体采用对数螺旋面式滑动破坏模式,其分析模型如图1 所示。其中,桩体与滑面交点为A 点,对数螺旋破坏面BC 与坡体滑面交于B 点,受荷段前侧土体对破坏体ABC 的作用简化为倾斜滑面AB 上的外荷载。这样,确定桩体嵌固深度问题可表述为寻求使桩体嵌固段前侧设计侧向压力最大值不超过该部分土体极限抗力值的桩体最小嵌固深度。
对图1 所示的分析模型,桩体嵌固段前侧土体极限抗力可运用塑性极限分析上限法[15]求解。其中,对数螺旋面BC 方程可写为:
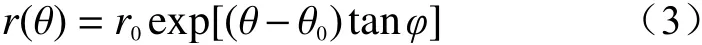
式中:r0——转动中心O 到滑面起点C 的距离;
θ0——OC 线与竖直方向的夹角;
ϕ——桩体嵌固段前侧土体内摩擦角。
在土体ABC(破坏机构)绕O 点以角速度ω 旋转达到极限状态时,对于作用于该滑体上的外力功率EW,采用叠加法,通过进一步推导,可得其表达式为:

式中:W1、W2、W3——对数螺线区域OBC、三角形区域OAC、三角形区域OAB 的虚拟土体(实际土体在ABC区域)的重力功率;
W4——推力Ru(等于桩体嵌固段前侧土体极限抗力)所作的功率;
W5−沿滑面切向力与法向力功率之和。
其表达式为:
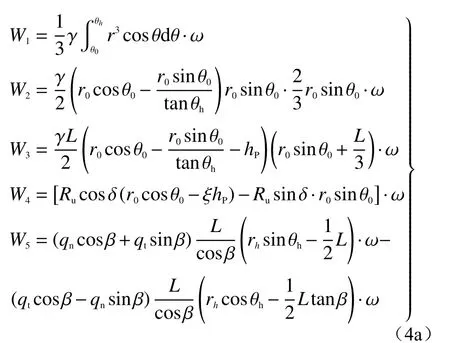
式中:γ——滑床土体重度;
L——滑面剪出口B 点距桩体的水平距离;
θh——OB 线与竖直方向的夹角;
rh——转动中心O 到B 点的距离;
ξ——推力Ru作用点到C 点的高度与AC 段深度hP的比值,一般可取为1/3-1/2;hP值可对嵌固段的刚性桩采用弹性地基梁法[12]计算确定,不再赘述;
V−滑动面BC 上各点的线速度,等于各点处的极径r与ω 乘积;
β——桩前滑面倾角;
δ——桩前侧面与滑床土体间的外摩擦角;
qn、qt——桩前坡体滑面AB 上的法向与切向应力。近似采用上覆土体作用平均应力法,可按式(4b)计算。

同时,破坏机构ABC 内能损耗发生在速度间断面BC 上,能量损耗率ED为:

式中:c−桩体嵌固段前侧土体黏聚力。
根据上限定理[15],外力功率与内能损耗率相等,得:

把式(4)(5)代入式(6),整理可得Ru的函数f的表达式为:

这样,在θ0和θh变化过程中,被动极限抗力Ru存在极小值的条件为:

将式(7)代入式(8),进行两个方程联立求解,可得被动极限抗力Ru的最小值。
于是,根据上述计算方法可得到抗滑桩不同嵌固段深度时桩前土体侧向极限承载力的合力。进而将所得的随嵌固深度变化的系列结果对深度求一阶差分,即可得到桩侧土体极限状态下相应于不同嵌固深度处的桩侧土体可提供的极限侧向压应力(简称极限压应力)。由于随着桩体嵌固深度的增加,该极限压应力(抗力)逐渐增大,而同时嵌固段桩前侧土体的设计压应力最大值则逐渐减小,因此,可取二者相等时的嵌固深度作为桩体最小嵌固深度。

图1 桩前倾斜滑面的嵌固段前侧土体受力分析模型Fig.1 Analysis model of stable layer with oblique top surface in the downslope area of embedded segment of anti-slide piles
2 工程实例
如图2 所示,某滑面呈折线型的滑坡的滑体为较为松散的第四系块石质土,滑床为侏罗系中统遂宁组(J2sn)强风化粉砂质泥岩,可视为较密实的土层(类土层)。坡体前缘地面相对平坦,强风化粉砂质泥岩裸露可见,坡面几乎无植被。坡体后缘与基岩断开形成约5 cm 高的错台。坡面近似呈折线型,中后部坡面倾角为27°,前部坡面倾角为40°,现场地质勘查确定块石质土与强风化粉砂质泥岩界面为滑面。采用现场环刀法和现场直剪试验方法,分别测试块石质土与强风化粉砂质泥岩的重度与抗剪强度参数,获得滑体与滑床的重度、内摩擦角和黏聚力分别为21.5 kN/m3、30°、5 kPa和22 kN/m3、38°、20 kPa。对该滑坡拟在坡体前缘设一排悬臂式抗滑桩加固,设桩处滑体厚度约为10 m,桩前滑面倾角为28°。桩体采用C30 混凝土浇筑,桩身截面尺寸为2 m×3 m,桩体抗弯刚度为1.08×108kN∙m2;桩中−中间距为7 m。根据地层岩性与现场经验[5],在桩前水平滑面条件下,滑床顶面侧向地基系数取为KA=20 000 kN/m3,滑床的地基系数比例系数取为m=40 000 kN/m4。考虑抗滑桩的布置,取一个桩间距范围内的滑体作为分析对象,按前述方法分析桩体嵌固段深度h2。
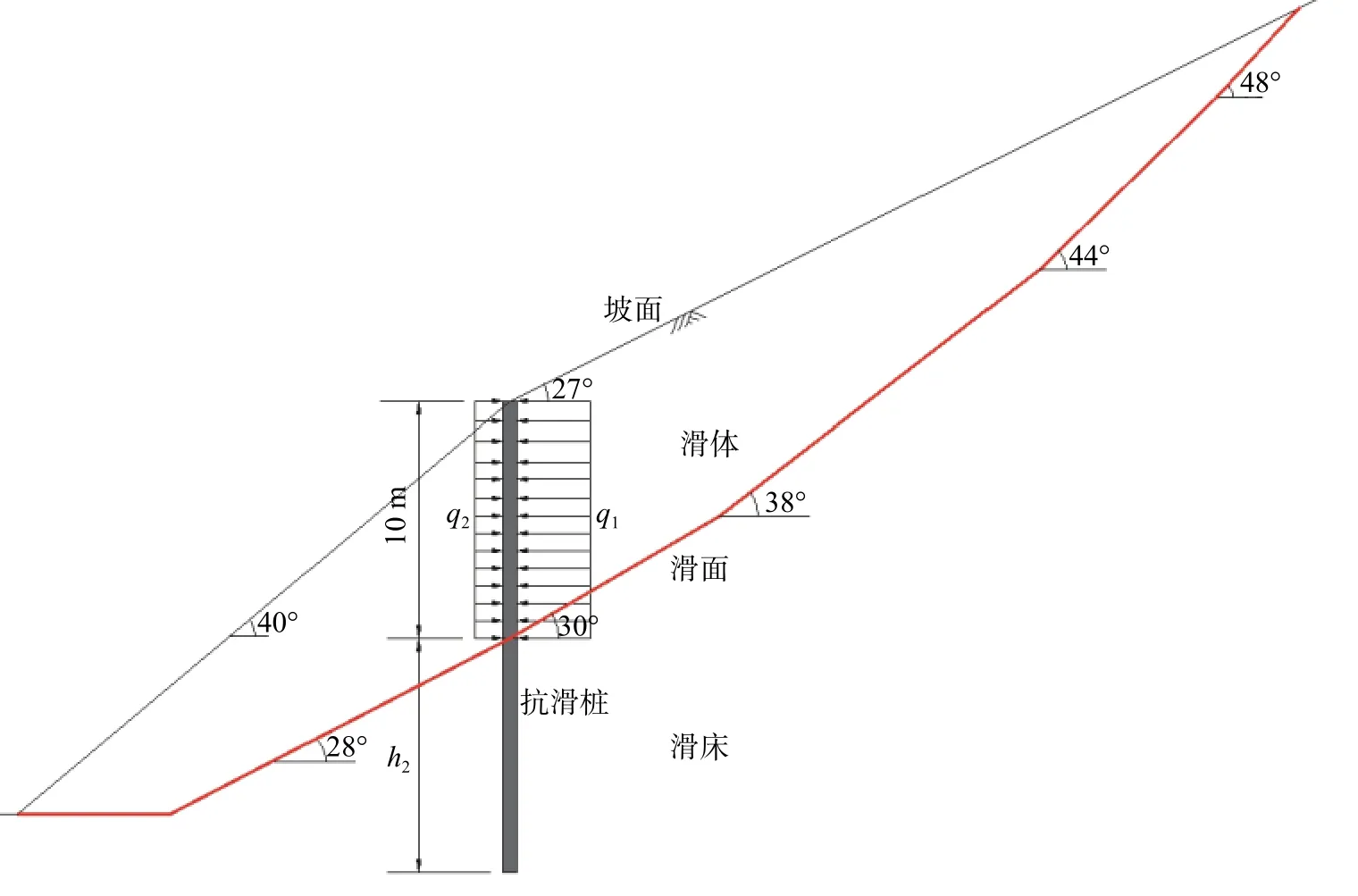
图2 抗滑桩加固某滑坡实例示意图Fig.2 Sketch map of a landslide example reinforced with anti-slide piles
桩后设计滑坡推力和桩前设计坡体抗力均按矩形分布,在设计安全系数为1.25 的情况下,桩后滑坡推力约为q1=640 kN/m,桩前坡体抗力约为q2=134 kN/m。
由于实际滑面呈倾斜状态,按照倾斜地面条件下地基侧向抗力系数的比例系数mβ取值算法[16],可得mβ=32 000 kN/m4。从而,采用地基系数法计算得到嵌固段桩前侧地层设计最大压应力σmax随嵌固深度h2变化曲线如图3 所示。同时,根据前述理论分析方法,可得嵌固段地层侧向极限压应力随深度变化曲线(图3)。由图3 中两条曲线的交点可见,对于本例,抗滑桩最小嵌固深度为8.59 m,取为9 m 时得到此时桩体内力如图4所示,桩身最大弯矩与剪力分别约为31 728 kN·m 与7 423 kN。若按规范中不考虑与考虑滑面倾斜的方法[13]计算(图3),可得抗滑桩最小嵌固深度分别为7.42 m与10.45 m(按桩前侧滑床土体极限抗力等效确定综合内摩擦角为40°)。可见,本文方法介于该规范中两种算法之间,且相对偏于式(1)的计算结果;相对于本法,式(2)计算结果偏于保守,而式(1)计算结果显然偏于不安全。本滑坡实际工程治理中抗滑桩嵌固段深度按本文计算结果取值为9m,治理后坡体稳定,治理效果良好,一定程度上说明了本文方法的合理性。

图3 嵌固段桩前侧地层压应力最大设计值与极限值随嵌固段深度变化曲线Fig.3 Inserted-depth-dependent variation curve of design maximum lateral stress and the ultimate loading capacity on the stable layer in the downslope area of embedded segment of the pile in the example
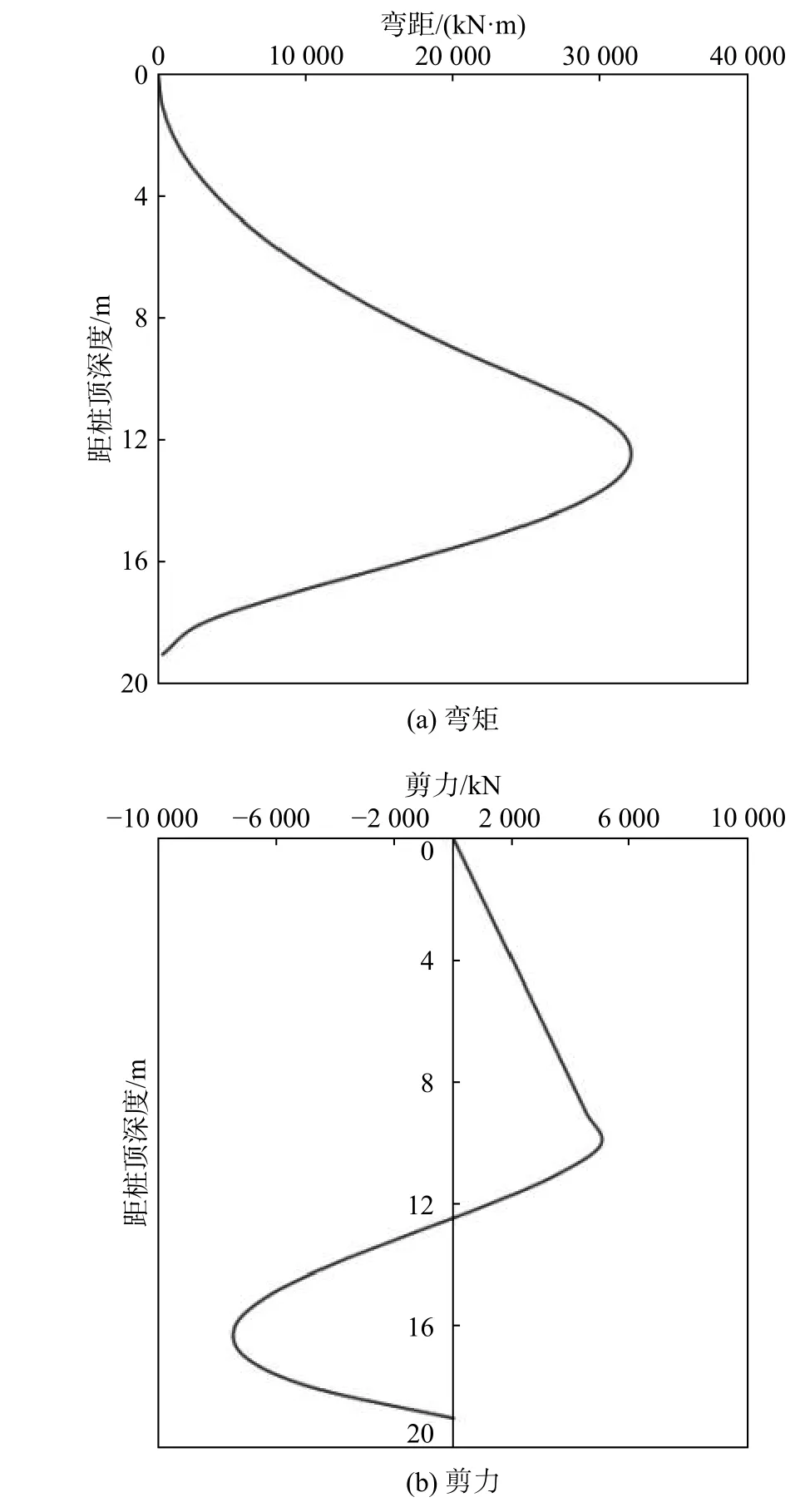
图4 本法确定最小嵌固深度时抗滑桩内力Fig.4 Internal forces of a anti-slide pile under its minimum inserted depth in the example by the proposed method
3 影响因素分析
由前述分析可见,抗滑桩的嵌固深度与桩前滑面倾角、嵌固段地层物理力学参数、滑坡推力、桩体力学性质等因素密切相关。为进一步探究这个问题,针对上述实例,采用控制变量法,主要讨论桩前滑面倾角与嵌固段地层物理力学参数对桩体最小嵌固深度的影响。
(1)桩前滑面倾角
根据文献[16]方法,可得到地基系数比例系数随滑面倾角变化关系,进而采用前述分析方法得到桩体最小嵌固深度随滑面倾角变化曲线如图5 所示。可见,最小嵌固深度随滑面倾角的增大呈非线性增加,在0°~10°范围内,曲线较为平缓,滑面倾角对嵌固深度影响较小;当滑面倾角超过10°时,最小嵌固深度增长速率逐渐变大,在10°到30°范围内,最小嵌固深度增加量显著。图5中也给出了按式(2)所得的计算值,可见,两种方法所得的曲线变化趋势相同,而本文方法所得最小嵌固深度整体上比规范方法所得结果小约18%。

图5 不同滑面倾角下抗滑桩最小嵌固深度Fig.5 Minimum inserted depth of a anti-slide pile under various dip angles of slip surface
(2)嵌固段地层黏聚力
图6 为在嵌固段土体不同黏聚力时桩体最小嵌固深度随滑面倾角变化曲线。可见,抗滑桩最小嵌固深度与土体粘聚力呈负相关的关系,且粘聚力对最小嵌固深度呈显著非线性影响。
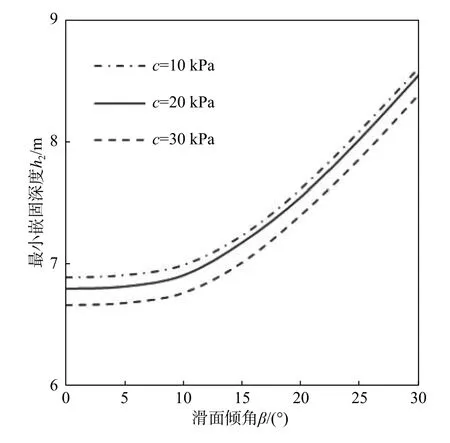
图6 不同黏聚力下最小嵌固深度随滑面倾角变化曲线Fig.6 Variation curve of minimum inserted depth of a pile with dip of slip surface under various cohesions
(3)嵌固段地层内摩擦角
图7 为嵌固段土体不同内摩擦角时最小嵌固深度随滑面倾角变化曲线。可见,抗滑桩最小嵌固深度与内摩擦角亦呈负相关的关系,当滑面倾角较小时(10°以下),随着内摩擦角增大,最小嵌固深度呈非线性减小;随着滑面倾角的增大,内摩擦角对最小嵌固深度影响的非线性特征减弱。

图7 不同内摩擦角下最小嵌固深度随滑面倾角变化曲线Fig.7 Variation curve of minimum inserted depth of a pile with dip of slip surface under various internal friction angles
(4)嵌固段地层重度
图8 为嵌固段土体不同重度时最小嵌固深度随滑面倾角变化曲线。可见,抗滑桩最小嵌固深度与土体重度呈负相关的关系。

图8 不同重度下最小嵌固深度随滑面倾角变化曲线Fig.8 Variation curve of minimum inserted depth of a pile with dip of slip surface under various unit weights
4 结论
根据抗滑桩计算地基系数法中倾斜地面条件下的“m”法以及塑性极限分析法,分别得到桩前倾斜滑面时抗滑桩嵌固段土层的设计压力与极限抗力,由此可确定出抗滑桩的最小嵌固深度。通过分析,主要得到以下结论:
(1)随着抗滑桩嵌固深度的增大,桩前侧最大设计压力逐渐减小,而极限抗力逐渐增大,二者相等时的嵌固深度即为在相应设计条件下的桩体最小嵌固深度。
(2)抗滑桩最小嵌固深度随桩前滑面倾角呈非线性增大变化趋势,在倾角为0°~10°范围内变化梯度较小,而在10°~30°范围内,最小嵌固深度变化梯度急剧增大。
(3)桩前倾斜滑面情况下,抗滑桩的最小嵌固深度与嵌固段地层的物理力学参数密切相关,最小嵌固深度随其粘聚力、内摩擦角和重度的增大而整体呈非线性减小。
(4)实例分析表明,与规范考虑滑面倾斜的建议方法计算结果相比,本文方法所得的桩体最小嵌固深度约小18%。
