一维等离激元晶格中的能带结构调控
2021-08-26曹凤朝吕博昆丁宇峰石锦卫
曹凤朝,吕博昆,丁宇峰,2,石锦卫
(1.北京师范大学物理学系,应用光学北京市重点实验室,北京 100875; 2.季华实验室,佛山 528000)
0 引 言
近二十年来,表面等离激元及其交叉学科由于其特殊的近场增强特性成为了光学领域的热门话题之一。等离激元具有将电磁波聚集到深亚波长体积的能力,推动了其在纳米光子技术和研究工作中的应用,各种无源和有源等离激元光子器件为产生、引导、调制和检测光信号提供了新的途径[1]。其中,贵金属(特别是金和银)中的表面等离激元的本征能量落在可见光频率范围内,这使得它们成为表面等离激元研究领域的热门材料。古罗马时代引人入胜的“莱克格斯杯”可能是表面等离激元效应的最早证明之一。杯子中的玻璃含有纳米量级的贵金属及合金颗粒,根据光源方向的不同会显示出不同的颜色和图案。
1857年,为了解纳米量级的金属粒子的光学响应,Faraday研究了金胶体溶液,意识到其光学性质与金粒子的尺寸有关。1902年,Wood[2]在研究金属光栅的反射时发现,当光源采用连续偏振光时,会出现反常的衍射行为,这一行为被称为“伍德异常衍射现象”。1904年,Garnett等[3]利用金属中自由电子的共振荡模型,解释了利用金属氧化物粒子制备“彩色玻璃”的原理。1908年,米氏理论被提出用以计算纳米颗粒的光学性质[4]。
但直至1956年,“plasmon”这一名词才被David Pines提出。分析固体薄膜散射快电子时观察到的某些特征能量损耗的问题,发现能量损耗是由金属内的自由电子整体振荡引起的,这与气体中观察到的等离子体电子气振荡行为非常类似,因此David Pines引入术语“plasmon”来描述这种高频集体运动[5]。1957年,Ritchie在研究高能电子穿过无限大金属箔出现的能量损耗问题时,发现单位厚度的能量损耗与金属厚度成反比。为解释这一现象,Ritchie提出了“金属等离子体”这一概念,并表示等离激元模式可能趋近于金属表面[6]。而后,在1959年,Powell和Swan 通过实验验证了Ritchie提出的理论。1968年,德国物理学家Otto 和Kretschmann 分别利用衰减全反射的方法从实验上激发了表面等离激元,并且测量到其色散曲线[7-8],这些方法至今依然被实验室所采用。
虽然米氏理论是在100多年前发展起来的,但迄今为止,它仍是描述光与金属纳米粒子相互作用的重要理论模型。除此之外,研究人员基于电动力学理论开发了各种数值计算方法,如时域有限差分法(FDTD)、有限元法(FEM)、离散偶极子近似法(DDA)和格林函数法等。这些建模工具几乎适用于所有金属结构,如单一金属结构、光子晶体阵列、超表面等。随着扫描隧道显微镜(scanning tunneling microscope, STM)和扫描近场光学显微镜(scanning near field optical)的出现,等离激元及其相关的近场光学效应成为研究热点。
表面等离激元(surface plasmons, SPs)是指金属-介质(两种材料介电常数实部符号相反)界面处自由电子集体振荡的电磁模式[9]。根据金属表面的电子分布特性和传播特性,基本可以分为两大类:沿金属与介质界面传播的表面等离极化激元(surface plasmon polaritons, SPPs)和束缚在金属表面的局域表面等离激元(localized surface plasmons,LSPs),又称为局域表面等离激元共振(localized surface plasmons resonances,LSPRs),本文采取LSPRs这种称呼。
利用麦克斯韦方程可以求出SPPs的波矢kSPP:
(1)
式中:k0是自由空间中光子的波矢;εd是介质的介电常数;εm是金属的介电常数。图1表示了kSPP与k0的色散曲线关系,其中电介质是空气。从图中可以看出,在相同能量下kSPP始终大于k0,这意味着激发SPPs需要提供额外的动量来满足波矢匹配。实验室激发SPPs的常见方法主要有以下几种,第一种是利用棱镜耦合,就是前面提到的Otto 和Kretschmann的方法[7-8]。第二种涉及表面拓扑缺陷的散射引入的额外动量,如亚波长的突起或孔结构[10]。第三种则是在金属表面引入光栅阵列[11]。
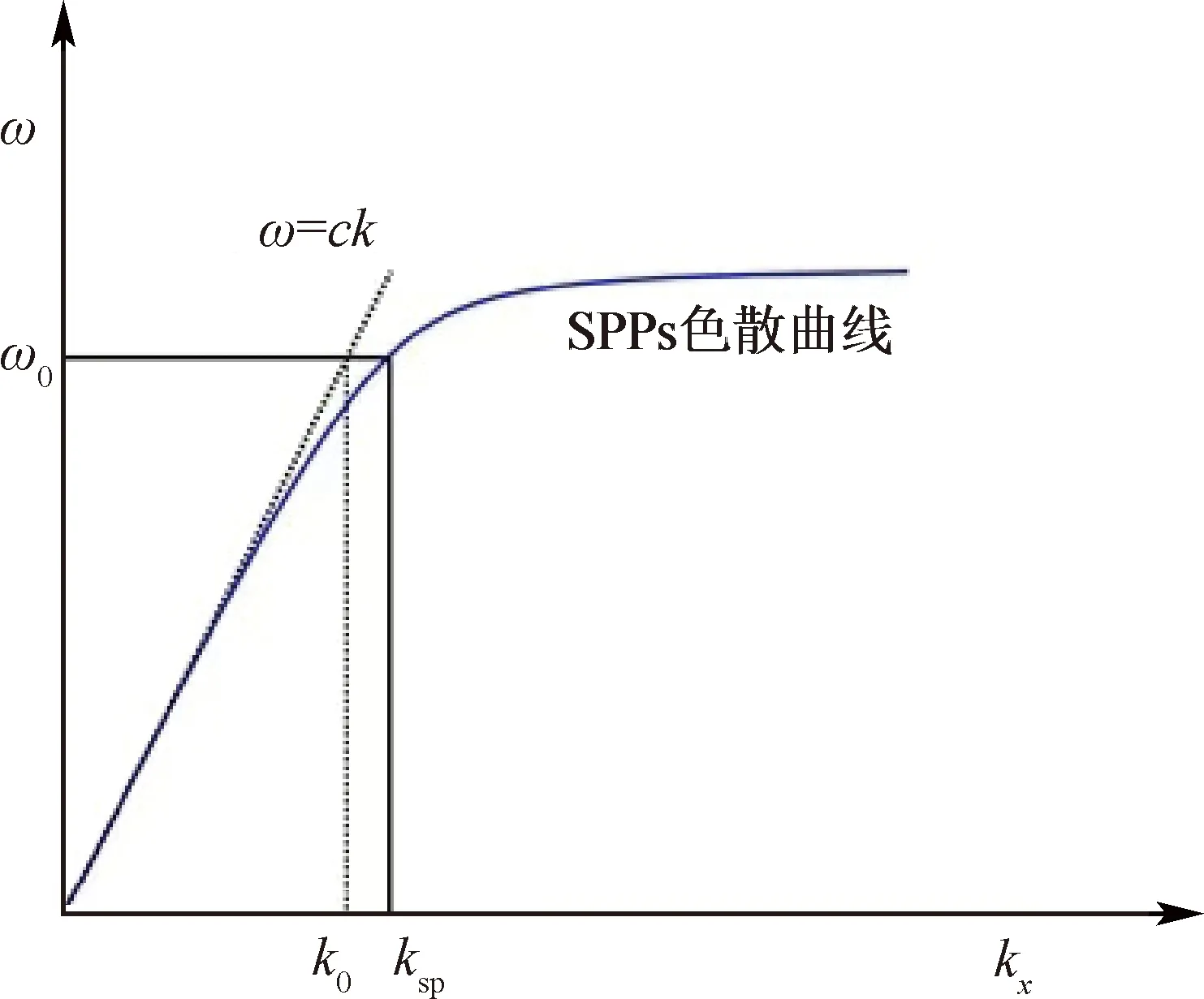
图1 自由空间中的光子与金属表面SPPs的色散曲线
光栅激发方式如图2所示。金属光栅对入射光进行衍射使得入射光与SPPs的动量匹配从而与SPPs进行耦合。并且,相反的过程还允许非辐射的SPPs模式与入射光耦合进行远场探测,这对开发基于SP的光子电路是至关重要的。

图2 光栅耦合激发SPPs
LSPRs是指在外部光场激发下局域在单个纳米结构周围的表面等离激元。当LSPRs被激发时,会形成近场增强效应,增大对入射光的吸收和散射。
事实上,一维等离激元晶格既支持表面等离极化激元SPPs又支持局域表面等离激元LSPRs,是研究表面等离激元及其光学性质的很好的基本结构。本文将以一维等离激元晶格为研究对象,分别从能带调控、表面晶格共振、连续域中的束缚态以及玻色-爱因斯坦凝聚四个方面阐述金属等离激元的新颖性质。
1 能带调控
能带理论最初是研究晶体中电子的状态及其运动的一种理论。在过去的几十年里,光子学的关键发展之一就是对光子带隙材料(photonic bandgap, PBG)的研究。这些人工材料使用波长尺度的周期结构来操纵光与物质之间的相互作用,从而构建新的光子结构[12]。这些发展主要是利用绝缘体和半导体材料的人工周期结构进行的。实际上,将能带结构与等离激元材料结合,也可以实现类似的等离激元光子带隙。
早在1996年,Barnes等[13]就提出了一个模型来描述波纹表面上SPPs传播中光子带隙的存在。当SPPs在周期与光波长成正比的金属表面传播时,其性质会发生变化。当纳米结构的周期是SPPs模式的有效波长的一半时,散射可能会导致驻波的形成以及SP禁带的打开,如图3所示。就像晶体固体中的电子波一样,一维金属晶格有两种SPPs的驻波解,它们具有相同的波长,但是由于不同的场空间分布和表面电荷分布,它们具有不同的频率,ω+和ω-。高频解ω+对应高能带,其表面电荷之间的距离更长且场分布具有更大的变形。而处于高能带和低能带之间的模式是不能传播的,被称为禁带。
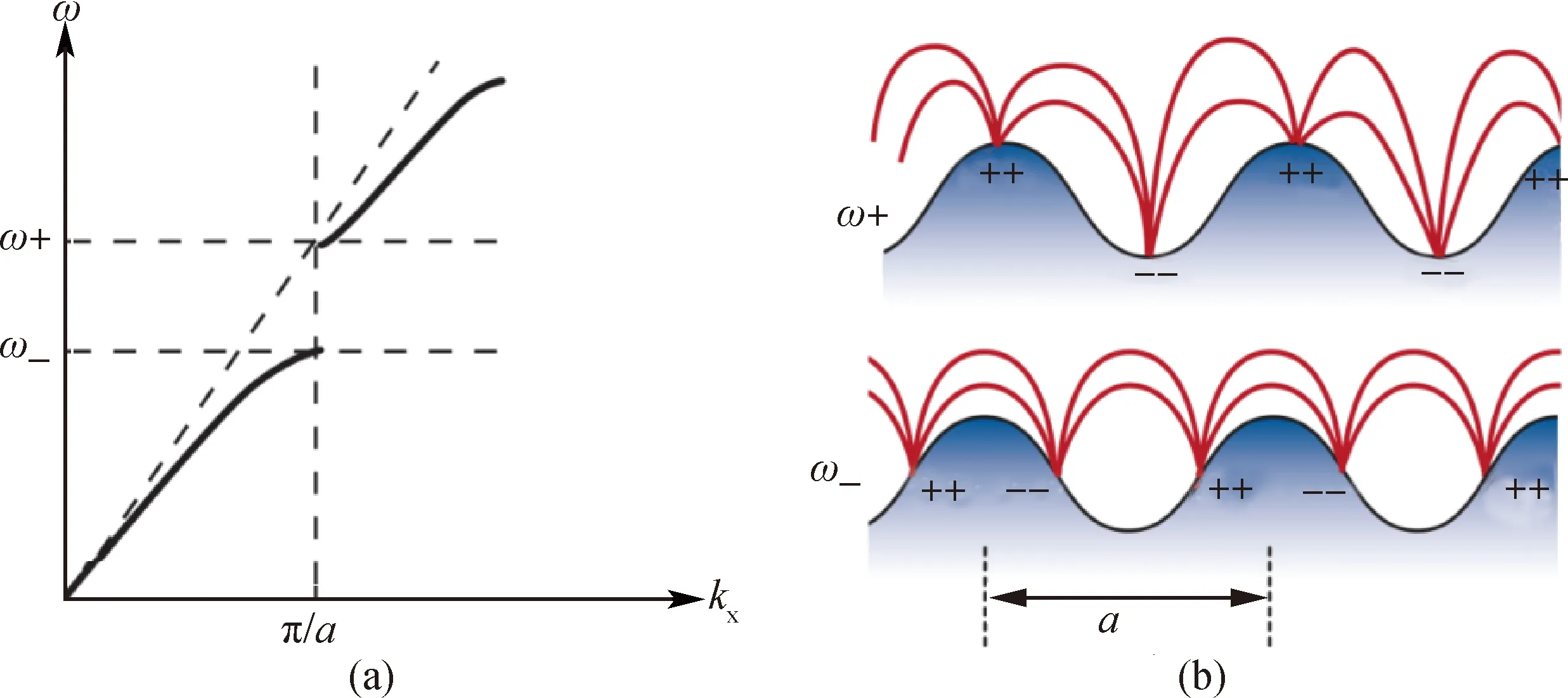
图3 (a)能带示意图;(b)周期为a的等离激元结构中的电子及电场分布示意图[12]
在证明SPPs与周期性结构的共同作用下可以产生光子带隙之后, Tan和Preist等[14]利用计算方法研究了短周期零阶金属光栅表面的SPPs能带和共振光学吸收。短周期金属光栅由一个窄高斯栅槽阵列组成,它的SPPs的色散曲线可以通过计算得到。光栅轮廓由公式(2)计算得出,
(2)
这个模型的优点是栅槽的深度d、宽度w、两个邻近栅槽之间的距离l都可以单独控制,共振频率可以通过改变这三组参数来选定。当深度为200 nm,宽度为10 nm时,作者计算了三组不同周期的高斯栅槽光栅的SPPs能带,周期分别为50 nm、75 nm和100 nm。Tan和Preist等通过计算发现当电磁波长远大于光栅周期和光栅深度时,可以观察到非常平的SP能带。这些平带来自局域在窄光栅栅槽中的耦合的LSPRs模式。而LSPRs模式与自由辐射的相互作用使光锥内的LSPRs模式变宽(辐射损耗增加),并使平坦的LSPRs能带在光锥线处产生强的反交叉现象。这里,光锥线指的是自由空间光的色散曲线,光锥线之上的能带可以与自由辐射波耦合,而光锥线之下的能带其模式无法辐射到真空中。与此同时入射电磁波激发这些零阶光栅的SPPs模式还会引起强烈的共振吸收。
继短周期金属光栅中的LSPRs能带被计算研究之后,Christ等[15]利用一维等离激元光子晶体平板从实验上实现了波导-等离激元共振,并使能带调控的范围达到强耦合的区域。波导-等离激元光子晶体结构是一种新型的杂化结构,由具有周期性的金属阵列和介质波导组成。因此既支持等离激元模式,也支持波导模式。这两种共振都会受到纳米尺度上样品几何结构的影响,因此,可以通过几何参数控制它们的相互作用。
这个一维等离激元光子晶体平板由一个介质波导和一个一维金光栅组成。为制备样品,作者首先在石英衬底上沉积ITO,然后在ITO上利用电子束刻蚀制备了不同周期的一维金光栅,光栅的周期范围为375 nm到575 nm,变化步长为25 nm。光栅的高度是20 nm,宽度是100 nm。光栅的面积是100 μm×100 μm。图4(a)显示的是实验几何示意图和SEM照片。当TE偏振光入射,对应的是图4(b)、(c)中的虚线和(d)中的星形。从图4(b)和(c)中可以看出,TE光入射时消光谱中的窄峰是由于TE准波导模式引起的,当降低ITO波导层的厚度时,则不会有这个模式出现。当TM偏振光入射时,对应的是图4(b)、(c)中的实线和(d)中的圆形。从图4(b)和(c)中可以看出,在1.9 eV处出现了一个较宽的峰,这是每一个单独的金纳米线导致的LSPR共振峰。还可以观察到一个较窄的TM0准波导模式形成的尖峰,在ITO层较薄时会消失。他们还发现,当改变角度或者周期时,这条宽的等离激元共振峰会与窄的TM0准波导共振峰显示出反交叉行为,形成了明显的能带劈裂。作者用耦合模理论唯象分析了LSPRs模式与波导模式之间的耦合并解释了能带劈裂的原因。耦合模理论是研究多个模式间耦合规律的理论,是波动物理一个普适的唯象理论,其模式可以是电磁波,也可以是机械波、声波、电子波函数;耦合模理论的本质是模式间的能量交换引起的希尔伯特空间坐标变换。

图4 一维等离激元光子晶体平板实现能带调控 (a)结构示意图及SEM照片;(b)入射光分别为TE偏振(虚线)和TM偏振(实线)时,周期为400 nm,ITO厚度为140 nm时的消光图;(c)入射光分别为TE偏振(虚线)和TM偏振(实线)时;周期为400 nm,ITO厚度为15 nm时的消光图;(d)入射光分别为TE偏振(星形)和TM偏振(圆形)时,在不同光栅周期下,计算(实心符号)和实验测量(空心符号)的消光光谱中最大值[15]
根据耦合模理论,整个系统的能量矩阵可以写为:
(3)



图5 一维等离激元光子晶体平板实现强耦合。(a)上:入射光激发的单个V形槽支持的LSPR模式。下:入射光激发的等离激元晶格支持的杂化模式。插图为结构的SEM照片。(b)单个SPP模式与LSPR模式耦合能带示意图,此时拉比劈裂能量为2g。(c)两个LSPP模式与LSPR模式耦合能带示意图,此时上带与下带拉比劈裂能量为不同周期下结构的动量空间角分辨反射光谱实验图[16]
用这种结构,同样利用耦合模理论,作者首先分析一个LSPR模式与一个SPP模式耦合的情况,整个系统可以写成一个如式(4)所示的哈密顿矩阵:
(4)
式中:ESPP和ELSPR分别代表SPP和LSPR模式;γSPP和γLSPR分别代表SPP和LSPR模式的阻尼速率,对应SPP和LSPR模式的半高全宽,g代表两个模式之间的耦合强度。当两个模式处于共振时,即ESPP=ELSPR=E0,系统的能量本征值可以被解出:
(5)
式中:UB和LB是两个模式耦合之后劈裂的杂化能带,对应的拉比劈裂为:
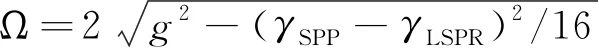
(6)
并且,劈裂之后的上带和下带在零失谐时具有相同的线宽,表明在SPP模式和LSPR模式之间的共振能量交换是相同的。进一步,当LSPR、LSPP的线宽接近时,对应的最大拉比劈裂为ћΩ=2g,如图5(b)所示。
当LSPR模式同时与两个SPPs模式耦合时,此时系统可以写成一个3×3的哈密顿矩阵:
(7)
式中:SPP1和SPP2是两个传播SPPs模式;gSPP-SPP是两个SPPs模式之间的耦合。通过解这个哈密顿矩阵,可以得到三模耦合之后的能量本征值为:
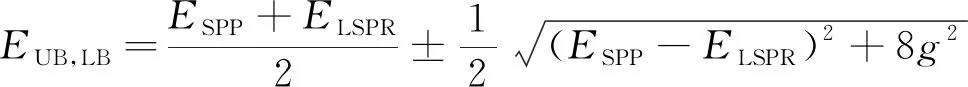
(8)

和介质光子晶体相比,金属晶格中等离激元的能带调控多了局域等离激元共振这个自由度。这个额外的自由度可以极大地改变晶格能带结构,从无传播的平带到无能隙的狄拉克点都可以实现。这一优点将会促进等离激元波导、滤波器、谐振腔的开发与应用。
2 表面晶格共振
基于LSPRs的等离激元模式有一个显著的局限性,它们品质因子Q较低(典型值Q<10,下文统称为Q值),这是由于在光学频率时金属中存在固有的欧姆损耗。Q值与光与物质的相互作用时间以及电场的增强有关,通常希望最大限度地增加这个量。因此,低Q值使得基于等离激元的超表面器件的许多潜在应用不现实,人们一直寻求在等离激元晶格中获得大Q值共振的新方法。
通过合理的设计,将纳米结构排列成晶格阵列时,在阵列中传播的衍射波会与单个纳米结构相关的LSPR耦合,从而产生阵列诱导的模式共振,称为表面晶格共振(surface lattice resonances, SLRs)[17]。这种共振会导致线宽急剧变窄,光谱线宽在某些波段甚至可降至几个纳米,从而形成Q值较高的等离激元共振。晶格阵列可以是一维或二维的,不过影响SLR特性的主要是某一个特定方向的周期排列,因此统一把它归结为“一维”晶格。
利用耦合偶极子近似模型(coupled dipole approximation, CDA)可以预测SLRs并阐述其基本性质。在这种近似中,用一个具有N个电偶极子的阵列代替一个具有N个纳米粒子组成的金属晶格[18]。对于一个无限大的全同粒子阵列,假设每个粒子的激发极化是相同的,那么每个纳米粒子的极化强度可以近似为:
(9)
式中:E0是入射平面波的振幅;αs是纳米粒子的极化率;S是纳米粒子的晶格求和项。阵列中每个纳米粒子的消光截面为:
(10)
式中:k=2π/λ是入射波的波矢。通过公式(10)可以预测,整个等离激元晶格的光学响应都与纳米结构的几何构型有关。通过改变纳米结构的几何构型,每个纳米结构单元的共振波长、共振强度、SLRs的Q值和线宽都可以被调控。
事实上,人们已经从实验上验证了影响SLRs的激发和Q值的因素,SLRs的Q值和线宽取决于阵列的周期、排列、阵列尺寸、粒子尺寸、周围的折射率匹配程度,以及尺寸的无序性,如图6所示。通过增大阵列周期,可以窄化SLRs线宽,增大SLRs振幅[19],如图6(a)所示。Humphrey和Barnes研究了银纳米粒子阵列中几种几何构型的SLRs。结果表明四方、三角和六角蜂窝晶格可以支持类似的SLR;就谐振线宽而言,没有特定的几何形状显示出优于其他几何形状的明显优势,如图6(b)所示[20]。使用上面概述的CDA模型,Rodriguez等发现SLRs的品质因数随着阵列尺寸的增加而增加,如图6(c)所示,当阵列的尺寸包含数百个粒子时响应达到饱和[21]。Fedotov等[22]从实验上探究了阵列大小与共振Q值的关系。他们发现,对于非对称同心劈裂圆环结构,阵列中晶格数目会对共振Q值产生明显影响。当晶格数目为32时,Q值仅为10.5。而当晶格数目增加至688时,Q值会增大至17.5。Le-Van等[23]通过实验证明,Q值可以通过改变纳米颗粒的尺寸来调节,如图6(d)所示。在可见光波段,通过将纳米棒的宽度从30 nm增加到56 nm,SLRs的Q值可以从98提高到325。Auguié等[24]在详细的理论研究中探讨了折射率环境对称/不对称问题。他们发现,通过将金属纳米粒子放置在对称环境中,例如通过添加匹配油以消除基底和覆盖层之间的折射率对比,促进了垂直入射下SLRs的激发。使用严格的电磁模拟,结果表明不对称环境会抑制垂直入射时的SLRs的激发,如图6(e)所示。图6(e)所示为反射率与基底到金纳米球阵列之间距离的关系。整体结构为浸入水中的金纳米阵列以及阵列下方的基底组成。从图中可以清楚地看出,随着基底与金纳米球阵列之间距离的增大,反射峰的强度会明显增大,Q值也会随之增大。

图6 表面晶格共振[17] (a)不同周期的不对称圆盘二聚体阵列的消光截面光谱,从左到右的四条实线对应的周期分别为350 nm、400 nm、450 nm和500 nm[19];(b)银纳米粒子阵列中三种几何构型阵列的消光光谱[20];(c)计算的SLRs的Q值与阵列中每个维度粒子数的函数[21];(d)具有相同周期不同宽度的银纳米棒阵列在垂直入射时的消光光谱,周期为px=340 nm,py=420 nm,宽度分别为30 nm、42 nm和56 nm[23];(e)计算的反射率与基底与金纳米球阵列之间距离的关系[24];(f)具有规则的位置,但粒子大小不同的纳米粒子阵列的消光光谱[25]
覆盖层与基片的折射率差以及阵列与界面的距离是决定衍射耦合强度的关键参数。一般来说,根据公式(9),SLRs的位置由S的实部和单粒子极化率倒数1/αs的实部的交点决定;而SLRs的强度和线宽则取决于S的虚部和1/αs的虚部之差。在不对称环境中SLRs受到抑制的主要原因是衬底产生的额外反射。对于电介质基底,这种额外反射对应的反射系数是纯实数的,只能与Re(1/αs-S)结合并相消,而对Im(1/αs-S)没有贡献。因此,在实部相消而虚部没有相消的光谱位置,SLRs被抑制[26]。事实上,认为折射率“必须”匹配这种观点仅适用于粒子高度相对较小的阵列。在这种情况下,粒子的等离激元共振的偶极矩被限定在阵列的平面内。由于偶极矩非常接近衬底和覆盖层之间的界面,相邻粒子相互作用的场横跨衬底和覆盖层,这两层折射率的对称性就很重要。然而,如果使用更高的粒子,并且光以倾斜角度入射,则可以激发垂直于阵列平面的偶极矩。在这种情况下,涉及相邻粒子之间相互作用的电场主要在覆盖层中,所以衬底和覆盖层之间的折射率失配不太重要[27-28]。最后,等离激元晶格中每一个纳米结构单元的位置无序性以及尺寸的无序性都会使SLRs展宽,如图6(f)所示[25]。
以上关于影响SLRs线宽及强度因素的探究基本都是基于入射光垂直入射到等离激元晶格表面的情况。而实际入射角度不同时,SLRs的光谱峰位会随着衍射边缘移动[30]。图7是Vecchi等测量的零阶透射/反射光谱与平面内波矢的关系。从图中可以明显看出,SLRs的共振位置会跟随波矢的变化而改变。因此,探究衍射边缘与SLRs光谱位置的相关性就显得尤为重要。Thackray等详细研究了垂直和倾斜入射时SLRs的性质,并发现存在两种普遍类型的SLRs,可以通过极化率倒数1/α以及共振附近的S(ω)来区分,如图8所示[25,31]。当S比较大,且Re(S)的曲线与Re(1/αs)的曲线相交时,可以观察到第一类SLR,如图8(a)~(c)所示。此时,在图8(c)中可以看到两个不相等的共振点P和Q,Q的共振强度要远远大于P的强度,因为P点处的Im(1/αs-S)要小得多。此时较强共振的位置偏离了衍射边缘的位置。第一类SLR通常在正入射时观察到。当Re(S)的曲线与Re(1/αs)的曲线不相交但是靠近时,可以观察到第二类SLR,如图8(d)~(f)所示。在这种情况下,可以看到在衍射边缘位置有一个极窄的Fano线形,衍射边缘对应着明显的场增强。第二种SLRs通常具有更高品质的线宽和强度,因为Im(1/αs-S)很小。第二种SLR通常在斜入射时观察到。

图7 (a)零阶透射光谱与归一化频率ω/c和波矢k‖的关系;(b)反射光谱与波长和波矢k‖的关系[29]

图8 不同结构参数下的金纳米球阵列的极化率倒数1/α、晶格求和项S实部曲线、虚部曲线以及对应的消光光谱。对应的结构参数为:(a~c)周期a=600 nm,半径r=80 nm,阵列位于玻璃衬底上,光源正入射到阵列表面;(d~f)周期a=700 nm,半径r=75 nm,阵列位于空气中,光源正入射到阵列表面[6,12]
表面晶格共振的有趣性质来自入射波电磁场的重新分布,通过使用等离激元光子晶体的衍射耦合,使得电磁场集中在阵列平面附近,这导致了表面晶格共振的一系列特性,如与LSPRs相比有更强的场增强、超窄的等离激元共振线宽、表面晶格共振的强消光等。等离激元晶格中支持的表面晶格共振会极大地增强光与物质相互作用。表面晶格共振与各种类型的分子和介质的耦合,有望在生物检测、光伏电池、光电通信器件、光催化以及超材料等方面有潜在的应用。
3 连续域中的束缚态
一个开放系统的本征状态,通常由一个或多个空间扩展的连续态和几个离散的束缚态组成。处于连续态中的波可以与外部场耦合,具有泄露通道,可以辐射至远场。而处于束缚态的波没有泄露通道,不能辐射至远场。连续域中的束缚态(bound states in the continuum, BIC)是一个特例,是一种频率存在于连续态却保持束缚态特性的非常规态。换言之,BIC处于光锥线以内却能实现完美局域。
由于等离激元较小的禁带宽度和很大的损耗,等离激元BIC的实现一直是个挑战。之前人们在很多系统中通过理论或者实验都能实现BIC态,低损耗体系如介质波导或者光子晶体,中等损耗如等离激元-光子晶体混合体系中(损耗补偿)实现BICs。但对于全金属的等离激元体系,由于金属固有的大损耗和小带隙,使得观测BICs成为困难,对其进行调控更是一种挑战,而且能支撑等离激元BICs的结构也很局限[32-34]。2018年,Azzam等[32]提出了在金属-介质混合结构中利用光学波导模式和等离激元模式的强耦合来实现BIC的理论方法,如图9所示,他们通过数值模拟展示了在第一布里渊区高对称点(Γ点)实现的对称性保护的BIC和在远离高对称点(Γ点)实现的Friedrich-Wintgen BIC。结构如图9(a)所示,该结构包含制备在石英衬底上的银浮雕光栅和顶部的二氧化硅覆盖层,光栅高度30 nm,宽度100 nm,周期400 nm,光栅底部的银膜厚度100 nm,覆盖层厚度500 nm。图9(b)为计算的该结构的角分辨反射光谱,蓝色点圈表示对称保护的等离激元BIC,红色点圈表示对称保护的光子BIC。当入射角度为11.4°时,在远离Γ点的白色点圈标记处出现Friedrich-Wintgen BIC,此类BIC是由于等离激元模式与光子模式的干涉和强耦合形成的。从反射谱中可以看到明显的能带反交叉现象,并伴随着150 meV的拉比劈裂。图9(c)~(e)给出了先前讨论的三个BIC周围共振峰的Q值,从上到下分别为受对称性保护的等离激元BIC、受对称性保护的光子BIC、Friedrich-Wintgen BIC的Q值。插图为角度稍微远离BIC位置时模式的电场分布。理论上,由于没有吸收损耗,对称保护的光子BIC的总Q值将会趋向无穷。而等离激元模式的Q值同时受到金属固有损耗和光辐射损耗的限制,因此等离激元BIC的总Q值将会趋向一个很高但是有限的数值。

图9 等离激元-光子模式实现BICs[32]
尽管提出了不少理论模型,但是等离激元的实验实现依然是一个挑战。最近的研究表明,可通过一维金属光栅结构中的强耦合,实现对全等离激元体系中的BIC的观测[35]。一维金属光栅可设计为强耦合系统,体系中的LSPRs模式与晶格表面SPPs模式在适当参数条件下进行能量交换甚至可达超强耦合状态[16]。通过系统研究两类模式之间的耦合,可观测到等离激元BIC并可对其进行调控。损耗的存在使得不同种类模式之间的有效相互作用长度有限,因此全等离激元体系中的BIC均为准BIC。
考虑有限尺寸结构中两模耦合的情况,由于结构的对称性,两个SPP模式除了波矢方向相反外,其余性质完全一样。将金属光栅类比于单层的光子晶体(介质光栅),考虑Γ点(k=0),由体系中哈密顿量的本征态可知,低能态由相位相反的两个SPP模式组成,对应对称性保护的BIC,该结果普适于等离激元与光子晶体结构[35]。然而由于金属的欧姆损耗较大,γ≫gbg(γ为LSPP模式衰减速率,gbg为两SPP模式的耦合强度),因此BIC通常被带隙之上高能态的亮模式所遮盖,以至于难以观测,如图10(a)~(b)所示。对此,可引入LSPR模式与亮模式形成强耦合系统,将亮模式劈裂成上下两个态,从而暴露出被隐藏的BIC态。
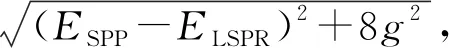
通过不断的调谐LSPRs模式失谐程度,还可观察到杂化带隙的闭合和再次打开过程。当闭合时,出现一个一维 Dirac点(在类石墨烯的能带结构中,比如光子晶体,当布里渊区某些点处的上下能带交叉闭合,带隙消失,交叉点即为Dirac点;这里位于中心对称点Γ处,且是一维结构,而石墨烯是二维的),如图10(f)中虚线椭圆标注,对应着BIC的消失。经过仔细分析,这里实际上对应一个能带的拓扑反转,对应于杂化带几何相位的转变,可通过Zak相位[36]来描述,结果如图10(j)~(n)所示。对于低能带来说,由于布洛赫态在Γ点为奇对称,因此体系中的Zak相位为π,随着光栅槽深度的增加带隙将关闭形成一维Dirac点,如图10(k)所示,此时Zak相位无法被定义;继续增加槽深度后由于强耦合的调控,带隙将再次打开,并且Γ点上能带的对称性被颠倒,导致能带的拓扑相变,如图10(l)~(m)。对称性保护的BIC总是在Zak相位为π的能带上,当形成Dirac点时BIC消失,对应拓扑转变点。这些现象表明,对于类似的结构来说,除了动力学相位产生之外,被激发的SPP也将具有额外的几何相位,可由LSPRs模式来进行调制,这种SPPs相位控制机制可以应用于片上光子和等离激元逻辑、开关器件[37]、非线性频率转换等。
除了对称性保护的BIC之外,体系中还存在非Γ点的BIC(k≠0),即Friedrich-Wintgen BICs。如图10(f)和10(o)所示,除了Γ点的BIC外(黑色虚线椭圆),还可以看到在任意两个LSPRs之间的杂化能带上存在明显的非Γ点BICs(虚线框标注)。图10(o)~(p)分别为同一样品的反射与衍射色散关系图,由于衍射光谱几乎没有背景信号且不受光学元件表面的反射干扰,因此断点对比度更高。对Friedrich-Wintgen BICs进行耦合模分析,得到在体系中所有原始模式所占比例,如图10(q)~(r),LSPR模式在k=±2.32 μm-1处出现完全干涉相消,而模型表明SPPs仍然存在,这与BIC的特性(不被远场探测)矛盾,说明了在该体系中耦合模理论作为一个唯象模型并不完备,需要重新考虑LSPP的物理机制才能理解BICs的出现。当远场光入射一维金属光栅上时,LSPRs模式可以被激发(存在共振或者非共振形式),所有金属槽中的LSPRs模式相互耦合生成LSPPs。当LSPRs模式共振时,LSPRs和LSPPs模式之间发生强耦合,形成对称性保护的BIC;当LSPR模式非共振时(非强耦合状态),周期光栅的散射也足以激发SPPs;然而,当所有到远场的LSPRs通道完全干涉相消时,SPPs并不会被激发,同时在远场也观测不到LSPRs和LSPPs模式,从而形成Friedrich-Wintgen BICs。当参与的LSPR模式更多时(槽的深度增加),能够明显观测到更多的Friedrich-Wintgen BICs成对出现,极大地改变了能带结构。

图10 一维金属光栅中实现BICs并对其进行调控[35]
理想BICs是一种无辐射损耗的模式,而Q值的大小又与体系的辐射损耗大小成反比,因此理想BICs的另一个重要特征是体系的Q值理论上是趋于发散的。但是理想BICs只能作为一种数学理想模型存在于无限大且无吸收的结构中。在实际应用中,受到样品尺寸、材料吸收、加工误差等因素的影响,准BICs通常存在一定的泄漏,其Q值也受限。以图10(o)为例,在接近BIC时,Q因子明显增加,反射法测量得到的最大值分别为62与51.4,如图10(s)~(t),由于金属槽数量限制(只有10个槽)、加工误差特别是反射率测量方法的缺陷等因素使得其小于仿真计算(Q>200,无限个金属槽)。无论是实验还是仿真结果,所获得的Q值都远远大于LSPR模式的Q值(~10),为实现高品质因子等离激元微腔提供了良好的思路。BIC和SLR都是获得高Q等离激元腔的方法。和SLR相比,BIC作为暗态,理论上有希望得到更高的Q值。通过选用单晶银作为等离激元材料以减小材料吸收,BIC的Q值有望得到进一步的提升[38]。在一维金属光栅体系中,可以完全自由地通过设计光栅周期或者槽的深度对两类等离激元BICs进行调谐和控制,这些额外的自由度使全等离激元体系成为研究BICs物理机制及应用的良好平台,包含低阈值等离激元纳米激光器、非线性效应放大器、高灵敏度传感器等。
4 玻色-爱因斯坦凝聚
玻色爱因斯坦凝聚(Bose-Einstein condensation, BEC),是指在某个单粒子模的分布可以由玻色-爱因斯坦分布描述的特定系统中,当低于某个特定温度或者高于某个特定的粒子数密度,大量玻色子在宏观上群居于某一特定的能量最低的模态,此时,所有粒子的动量、能量等参数可以用统一的相干波函数来描述,在动量空间表现为集聚在同一点。玻色和爱因斯坦最初提到的BEC是粒子处于平衡态的凝聚现象,在极低的温度下已经被证实。现在对于BEC的研究逐渐从平衡态(比如基态BEC)拓展到非平衡状态(比如激发态BEC)[40],通过获得激子极化激元(exciton-polariton, EP),可在室温下实现无需粒子数翻转的低阈值激光。
已经有很多工作报道了室温下的BEC激光[41-42],这些工作大多使用非金属晶格或者FP腔来获得光学模式,因为金属等离激元谐振的品质因子远低于介电微腔的品质因子。然而在开放系统中,金属等离激元系统表现出优于介质系统的BEC特征。如前所述,共振金属纳米结构产生的亚波长场增强现象可以显著增强光与物质耦合,因此激子与等离子体结构产生的电磁场强耦合会导致复合准粒子的形成,这种准粒子被称为等离激元-激子极化激元(plasmon-exciton-polariton, PEP)。
通过在金属纳米阵列超表面附着荧光分子,人们分别在弱耦合[43-44]和强耦合[45]区域观察到BEC激光。PEP产生的BEC主要有以下几个特征:(1)BEC发生在强耦合杂化能带带底,对于一维晶格,在k=0处;(2)当泵浦功率大于阈值,受激辐射弥补并超过了其他路径的衰减速率,辐射随入射光功率呈非线性增加,光致发光线宽减小,模式的空间和时间相干性急剧增加;(3)超薄结构,具有天然的开腔特点。
2017年Ramezan等[45]用光泵浦由薄有机分子层包裹的银纳米粒子阵列产生等离子极化激子BEC激光。有机分子中的激子与等离激元共振模式强耦合形成PEP,而金属纳米粒子阵列既支持暗模式,也支持亮模式,这项工作通过等离子体强耦合体系首次观测到暗模式BEC激光。
2018年Hakala等[39]使用金纳米颗粒阵列和染料分子结合,通过金纳米柱阵列产生的表面晶格共振模式和染料分子层的弱耦合,在有限尺寸,开放耗散系统中实现亚皮秒尺度的超快热化和凝聚,观察到了室温下的等离激元自身的BEC。同样是等离激元架构,但是和PEP类型的BEC不同,这是一个平衡态的BEC,如图11所示。将空间域光场分布的变化转变为时间域的演变,提取出特征时间,可以在较长的时间尺度上观测到能带结构中的热化过程、激光产生过程和BEC过程的演变,并区分了各自的物理本质。在BEC演化过程中观察到超过临界阈值后明显的谱线变窄、非线性以及增长的空间相干性等现象。通过调整结构参数实现能带结构的调控,最终实现从玻色-爱因斯坦凝聚到普通激光的转变,为室温下产生超快、低阈值片上激光展示了广阔的前景。

图11 (a)金纳米颗粒阵列和IR-792染料分子构成的超表面;(b)超表面光泵浦位置和信号收集区域,通过调整超表面结构参数实现能带调制,从而观察到热化机制,受激发射机制和玻色爱因斯坦凝聚机制的演化过程;(c)~(e)沿传播方向的原始信号强度;(f)~(h)图(c~e)中每一行的强度被该行强度总和做归一化处理[39]
5 结语与展望
本文系统地总结了一维等离激元晶格能带结构的最新研究进展,重点阐述了能带调控、SLR、BIC、BEC四个方面。由于局域模式与晶格模式的强耦合,即使周期固定不变,等离激元的能带也可以被极大地调控。等离激元的高损耗使得其对于高Q模式的需求非常急迫。SLR和BIC分别从亮模式、暗模式两个角度论证了获得窄线宽模式的方法。等离激元晶格的这些特性既可以用实现非平衡态的激子极化激元BEC,也可以用于平衡态的等离激元BEC。
强耦合后的模式能带与单独的SPPs或者LSPRs相比,具有更多的优越性。与SPPs相比,其具有更强的场增强、更平缓的能带,因而具有更小的群速度,以及可开关的带隙。与LSPRs相比,其具有更强的场增强、超窄的等离激元共振宽度、强吸收。强耦合调控了能带,利用杂化能带在动量空间的分布形成的角度依赖的吸收曲线,可以设计特殊的空间滤波器,比如针对特定时间频率分量的空间频率滤波器,可用于对特定波长光场的空间分布进行调控。同时,这种调控对应数学上的函数变换,因此新能带可以用于光学模拟计算,如微分器、积分器等。
新的杂化模式还可以用于集成光学。等离激元材料直接用作超薄集成光学波导一直存在吸收损耗过大的问题,不过单晶银的制备可以一定程度上减少吸收损耗。目前文献报道,在红光到近红外波段,等离激元在单晶银板上可以传播超过100 μm,可以用于制作逻辑门、全光开关等器件。如果将等离激元和波导耦合,传输损耗还可进一步降低,而能带调控可以用于控制带隙、群速度、传播方向等性质。
等离激元的近场增强效应一直被用来增强各类非线性信号,包括谐波产生、四波混频、克尔效应及其诱导的光开关、自聚焦、自散焦、自相位调制、交叉相位调制等。能带调控可以改变“局域”模式的间距,具有一定的“调谐”能力,可以用于实现多模共振增强,这对于高效非线性过程非常有利。
能带强耦合诱导的SLR与BIC态都具有很高的Q值,同时保留了等离激元强烈的近场耦合效应,对于基于等离激元谐振腔的应用,如等离激元激光器(spaser)、纳米尺度腔与物质相互作用研究、基于耦合模式的级联极化激元产生、芯片上高效量子光源等,具有非常重大的价值。
通过将晶格杂化模式与各种类型的分子和介质耦合,可以实现超灵敏的生物化学环境检测、高效的太阳能光伏器件、水分解、新型光电和通信调制器件、可调谐的滤波器件、高效的光催化、节能的液晶和显示器件。这些方面的研究空间依然很宽广。
