基于多目红外视觉的室内无人车导航系统研究

周颖文 王 勇，2

（1.江苏师范大学电气工程及自动化学院，江苏 徐州 221116；2.徐州市质量技术监督综合检验检测中心，江苏 徐州 221000）

0 引言

随着工业4.0概念和《中国制造2025》战略文件的提出，智能制造工程领域被列为重点发展对象。目前，在国内智能制造工程领域中，机器人产业规模正加速增长[1]，已成为世界最大的机器人市场。其中，室内无人车的需求量逐年上升，无人车导航的精度问题成为目前重点研究的对象。高精度导航无人车能够精确地提供时间和空间信息，从而提高生产生活效率，无人车市场还将不断扩大，具有广阔的发展前景。然而，由于我国机器人行业起步较晚，高精度导航定位系统发展较慢，导航定位系统的精度可靠性较低，国外高精度导航定位系统成本较高，因此制约了我国高精度机器人导航系统的发展。

基于上述研究背景，综合考虑成本、精度等原因，该文对一种低成本、高精度且实时性较好的多目红外系统进行研究，并使用该系统实现室内无人车的高精度导航定位。在该文中，使用一维标定杆对多目红外系统进行标定，计算多目红外系统的相关参数，并设计无人车控制系统，完成轨迹规划。研究表明，该系统能够准确地计算出空间点的位置信息，实现室内无人车定位导航。

1 多目红外系统

该文使用Optitrack公司的Prime13红外相机进行实验。使用三脚架将多个红外相机置于高处，为了使多目相机系统的观测范围达到最大，且保证实验场地中心能被多台相机同时观测到，将多台相机环形摆放。

将大于3台相机的系统称为多目系统，该文实验中使用相机个数为8台。使用多目红外系统需要首先对其标定进行研究。标定是获取空间位置信息的重要过程，通过标定，可以获取相机的位姿和内部参数，再结合相关视觉理论重建空间三维信息，从而实现空间定位。目前，根据标定物的不同，标定方法可以分为3种：三维标定块、二维标定平面以及一维标定杆[2]。该文使用一维标定杆标定法对多目相机进行标定，这种一维标定杆加工制造简单，生产成本较低，相机可以在视场内获得标定杆的任意位置数据来进行参数计算，数据获取速度较快、效率高，同时，使用这种一维标定杆进行标定，可以大大减少标记点在识别和提取过程中产生的误差。因此，一维标定杆标定法广泛应用于在较大空间内对多目相机的标定。该文所使用的一维标定杆如图1所示，由3个特殊材质制成的高反光小球A、B和C组成，用来反射红外相机发射的红外光线。每2个小球之间距离不同，但处于同一直线上，AB距离为175 mm，BC距离为325 mm。

图1 一维标定杆示意图

一维标定杆还具有可手持的优势，能够在短时间内在较大场地内自由运动，方便相机采集大量数据进行计算，大大提高了参数计算的速度和在大空间中进行标定操作的便捷性。

2 系统标定

在一维标定杆标定算法中，首先需要对相机成像平面图像进行二值化处理，使标记点的成像点与周围坏境的成像形成较大亮度差，以便突出标记点在成像图像中的位置，进而提取标记点的像素坐标。具体操作步骤：将图像上256个亮度等级进行阈值设置，使像素点灰度值仅存在0和255，此时成像图像中仅有标记点显示为白色。由于受噪声和相机镜头畸变的影响，在二值化成像平面中显示的标记点的成像点可能是一个不均匀的近圆图像，因此需要对二值图像中的标记点提取像素边缘，再将提取后的近圆图像拟合成圆，最后求解该圆的圆心坐标，其圆心坐标做为标记点的二维像素坐标[3]。

一维标定杆上的标记点在多目相机下投影到成像平面上的示意图如图2所示。记Aj、Bj和Cj为标记点A、B和C在空间中运动时在不同位置产生的空间点，j=1，2，3，…，N。Oi为第i个相机的光心，i=1，2，3，…，m。标记点在相机成像平面中的成像点分别为aij、bij、cij。建立关于空间点和相机位姿的重投影误差函数，对重投影误差进行整体优化，相机参数为优化变量。最小化重投影误差函数即可得到最优的相机参数解，建立的重投影误差函数如公式（1）所示。

图2 一维标定杆多相机成像示意图

使用稀疏LM（Levenberg-Marquardt）算法[4]对重投影误差函数进行优化求解。为了提高参数求解的准确度，根据标定杆一维线性的性质，以标定杆上的Aj点为原点建立球坐标系，根据球坐标与直角坐标的转换关系为x=rsinϕcosθ，y=rsinϕsinθ，z=rcosθ。其中，r为某一点到球坐标系原点的距离，某点到原点的连线与正z轴之间的夹角为ϕ，该连线在xy平面的投影线与正x轴之间的夹角为θ。该文中，Aj为原点，那么Bj的球坐标中r值为175，同理Cj的r值为500。由于3个标记点都在一条直线上，因此Bj、Cj点球坐标的ϕ、θ一致。该空间中Bj、Cj的球坐标如公式（2）所示。

将式（2）带入相机成像模型表达式[3]，得到aij、bij和cij的球坐标表达式，再根据公式（1）进行参数求解。

仿真中的相机硬件参数为焦距5.5 mm、图像分辨率1280×1024，根据该参数，可以计算得到相机实际内部参数值：fx=178.571 pixels，fy=178.571 pixels，u0=640 pixels，v0=512 pixels。根据系统标定过程，采集真实场地下标定杆在成像平面上的二维像素坐标数据，并依次计算2个相机、3个相机以及4个相机系统下的每个相机的内参值，结果见表1。

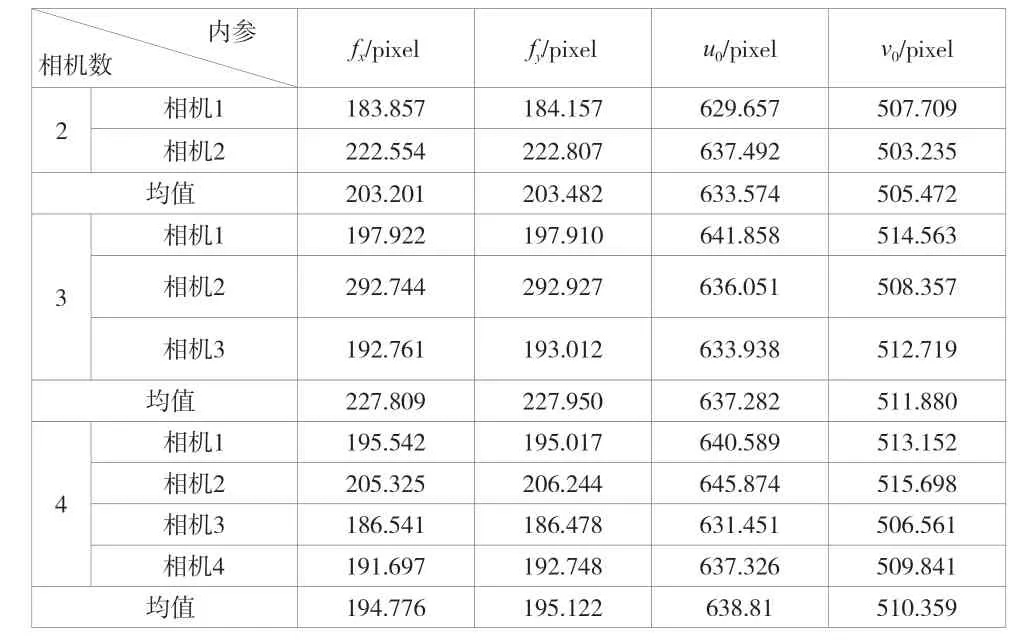
表1 不同相机数目组成的系统标定结果

将表1中不同相机数目下计算出的内参均值与实际内参值进行比较。以不同相机数目下计算出的fx参数结果为例，2台、3台和4台相机的计算结果的平均值分别为203.201 pixels、227.809 pixels和194.776 pixels，那么4台相机下的fx计算值与实际内参值误差最小。同理，将其他参数值进行比较，可以发现，在使用4台相机进行内参计算时，误差均小于2台相机和3台相机下的参数计数结果，可以说明4台相机对抑制噪声等干扰的效果较好，标定结果更准确。因此，可以通过增加相机数目来提高标定精度。

3 三维重建

经过上述过程可以得到相机的相关参数，即得到投影矩阵，再结合相机成像模型、求解投影矩阵的流程，可以将标记点从成像图像上的二维像素坐标恢复为空间三维坐标，该过程为三维重建的过程。根据相机成像模型，假设空间某点坐标为（X，Y，Z），将该点坐标写为齐次坐标[5]形式为（X，Y，Z，1），经过参数估计后，空间某点在一个相机下的投影公式如公式（3）所示。

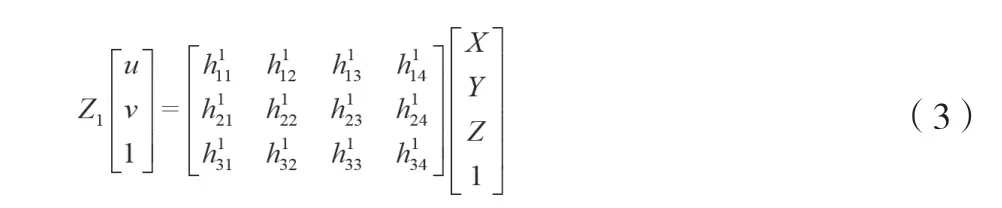
一般来讲，相机数目越多，根据投影坐标公式得到的约束方程组就越多，从而可以得到更加精准的空间点坐标。为了验证这一点，该文使用了精度为0.01 mm的云台，对多目红外系统进行位移定位准确度测量。测量结果发现，2台相机位移准确度可达0.53 mm，3台相机位移准确度可达0.43 mm，6台相机位移准确度达0.26 mm，8台相机的位移准确度可达0.10 mm。可以发现，相机数目越多，位移准确度越好。

4 无人车轨迹控制

该文所搭建的无人车控制系统硬件模块主要包括电源模块、控制器模块、CAN总线接口模块和电机驱动模块。控制器与电机通过CAN总线进行通信。其中，电机通过CAN总线向控制器传输数据时，需要要经过编码器将光信号转换为电信号进行传输。

使用STM32F103型号芯片作为控制器，在keil环境下进行控制编程，使用PID控制算法实现对基于麦克纳姆轮的无人车轨迹控制。根据麦克纳姆轮的运动学模型[6]，求出无人车4个轮子分别对应的旋转速度，作为控制量。4个轮子分别设置4组PID参数，以实现对4个麦克纳姆轮的PID控制，完成相应的运动指令。

在软件设计中，整个软件需要实现小车相关参数的测量与计算、CAN总线通信、上位机与小车的串口通信、PID控制以及小车工作状态监控等多项任务，这些任务都是通过软件端的前后台操作系统来完成的。系统在运行时，程序会不断在循环中调用相关函数来实现模块功能，通过设置的相关中断优先级来运行当前要紧急处理的任务，等中断任务处理完成后，再返回到中断点，继续运行该程序，循环往复。

在实验场地中使用八目红外系统对无人车进行运动轨迹捕捉，设置机器人圆周运动的半径为1000 mm，速度为0.3 m/s的圆周运动，采集连续运动3圈的运动轨迹。圆周运动测量结果和指令轨迹之间的偏差如图3所示，虚线表示指定轨迹，实线表示测量轨迹。

图3 圆周运动测量结果和指令轨迹比较

通过计算测量轨迹与指令轨迹之间的误差，可以得到最大误差为237.667 mm。对3圈轨迹中每相邻2圈的误差进行计算，发现相邻两圈均在水平方向产生最大误差，分别为90.137 mm、87.776 mm，但是每相邻两圈的误差变化较小。从测量结果中可以看出，使用PID控制算法控制基于麦克纳姆轮的无人车时，无人车在做水平方向运动时易产生较大的累积误差，该误差可能和轮子与地面之间的摩擦、传动机构的机械误差有关。

5 结语

该文提出了一套基于视觉的室内无人车导航系统，介绍了多目红外系统的定位流程，并通过对多目红外视觉系统的标定、空间位置进行计算，实现了对无人车的定位导航。经实验发现，使用一维标定法对多目红外系统进行标定，能够快速准确地计算出相机相关参数。同时，多目红外系统可满足室内10 m范围内的定位导航，且相机越多系统精度越高，8台相机的位移准确度可达0.106 mm。

该系统在其他工程领域也有较大的应用空间，可应用于无人车轨迹精度的测量，通过测量的误差结果，可以对无人车进行运动误差补偿，以提高无人车的定位导航精度，从而提高无人车的工作效率，也可用于其他机器人产品的运动精度测量，包括无人机等空间运动的机器人产品，能够为国内机器人相关产品提供一套标准的测试平台。