主成分分析和长短期记忆网络的电力负荷预测
2021-08-26吴定安钟建伟王新磊向家国曾凡伟
吴定安,钟建伟,王新磊,向家国,曾凡伟,胡 凯,陈 晨
(1.湖北民族大学 信息工程学院,湖北 恩施 445000;2.国网湖北省电力有限公司恩施供电公司,湖北 恩施 445000)
0 引 言
电力系统的稳定运行要求发电量和负荷的需求量实现供需动态平衡,但电力负荷的非线性特征明显且波动随机性较强,影响电力负荷消耗的因素多元,特别是气象因素对负荷的影响。相关研究表明,用电负荷预测的误差每增加1%,电力系统每年的运行成本将增加数千万元[1]。因此需要探究电力负荷的变化规律,提高电力负荷的预测精度是目前迫切需要解决的问题。
目前主流的电力负荷预测方法可以分为时间序列预测法和机器学习方法。其中时间序列预测法包含自回归求和移动法[2]、傅里叶展开法[3]、卡尔曼滤波法[4]等;其原理是根据历史负荷数据自身的时序性和自相关性进行预测,该方法不需要考虑负荷的相关因素且计算速度快,预测方法较为简单,但时间序列预测法预测精度较低。机器学习方法对非线性数据拟合较强,随着计算机技术的发展,机器学习方法是目前使用较为广泛的方法。文献[5]和文献[6]使用反向传播神经网络,参数拟合能力较强,但是对时间序列数据不敏感,算法效率低。文献[7]和文献[8]使用支持向量机的方法建立预测模型,虽然得到的解是全局最优,但在大规模数据样本上计算速度慢,计算效率低下。
近几年,随着深度学习的发展和广泛运用,深度学习算法被运用到电力负荷预测中。例如文献[9]采用深度信念网络进行预测,虽然预测精度得到了提高,但仍未很好地利用负荷数据间的时间序列信息。深度学习中的长短期记忆网络算法却可以高效利用数据间的时序信息,其泛化能力强,对较大和较小数据集都具有良好的学习能力,在处理非线性问题时优势明显。
本文对气象因素进行主成分分析(Principal Component Analysis, PCA),提出了基于PCA-LSTM电力负荷网络模型,旨在提取利于提高预测精度的有效信息,去除气象因素中的噪声,然后将获得的主成分和前一日的负荷数据输入LSTM网络中,不断进行电力负荷的滚动预测。通过利用真实气象因素数据和负荷数据,验证了该方法的有效性和可行性。
1 主成分分析
负荷预测模型的输入包括历史负荷、历史气象。输入特征间存在内相关性。采用PCA对气象数据进行主成分分析,获得的主成分可以代替原本的气象数据,不仅可以保留之前数据的基本信息,还可以去除影响神经网络预测的噪声[10]。
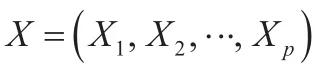

计算协方差矩阵的特征值λi及相应的正交化单位特征向量ai,原变量第i个主成分Fi为:

确定主成分个数m,则方差贡献率和累计方差贡献率分别为:
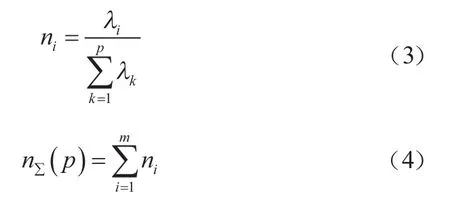
计算主成分载荷系数l:

计算各影响因素在m个主成分上的得分:

累计方差贡献率达到75%~90%时,对应前m个主成分能够包含原始负荷影响数据集中的大部分信息,因此主成分个数为m(m<p)个。
2 长短期记忆网络
LSTM神经网络可有效避免传统网络中梯度消失与梯度爆炸的问题。LSTM通过额外增加记忆单元,能够记忆过去的信息,进行长时间存储。LSTM的泛化能力强,对较大和较小数据集都具有良好的学习能力,在处理非线性问题时优势明显[11]。LSTM基本单元结构如图1所示。
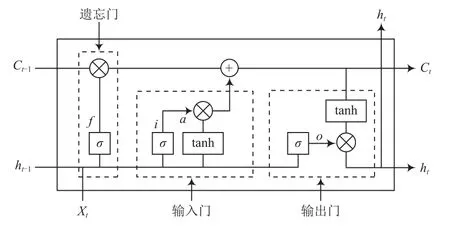
图1 LSTM基本单元结构
遗忘门ft根据上一时刻的状态Ct-1决定丢弃和保留的信息。输入xt分别经过σ和tanh决定要更新的数值并生成新的候选值,经过更新运算后的数值再与遗忘门ft一起更新单元状态。更新后的单元状态Ct经tanh函数与输出门ot运算后输出ht[12]。LSTM基本单元的状态更新方程见式(7)~式(11):


式中:xt和ht分别表示输入向量和输出向量;f、i、o分别表示遗忘门、输入门和输出门;Ct与Ct-1分别表示上一时刻与当前单元状态;ht-1与ht分别表示上一时刻与当前隐藏层单元的输出;σ表示sigmoid激活函数;tanh表示正切函数;W和b表示权重矩阵和偏差向量。
3 PCA-LSTM组合预测模型
3.1 模型结构
本文提出的PCA-LSTM负荷预测模型首先将获取的负荷数据和气象数据进行处理,然后通过PCA方法降维影响负荷的气象数据,将降维后的气象数据和负荷数据进行归一化处理。最后将归一化数据构造成数据集和测试集输入LSTM网络中进行训练和预测。
PCA-LSTM预测模型由输入层、隐藏层、输出层、模型训练层和模型预测层组成。将训练集的数据输入预测模型中,通过预测模型的不断训练达到最大迭代次数,模型各参数达到最优,此时模型预测效果最好;最后将测试集输入训练好的模型中得到预测结果。PCA-LSTM预测流程如图2所示。
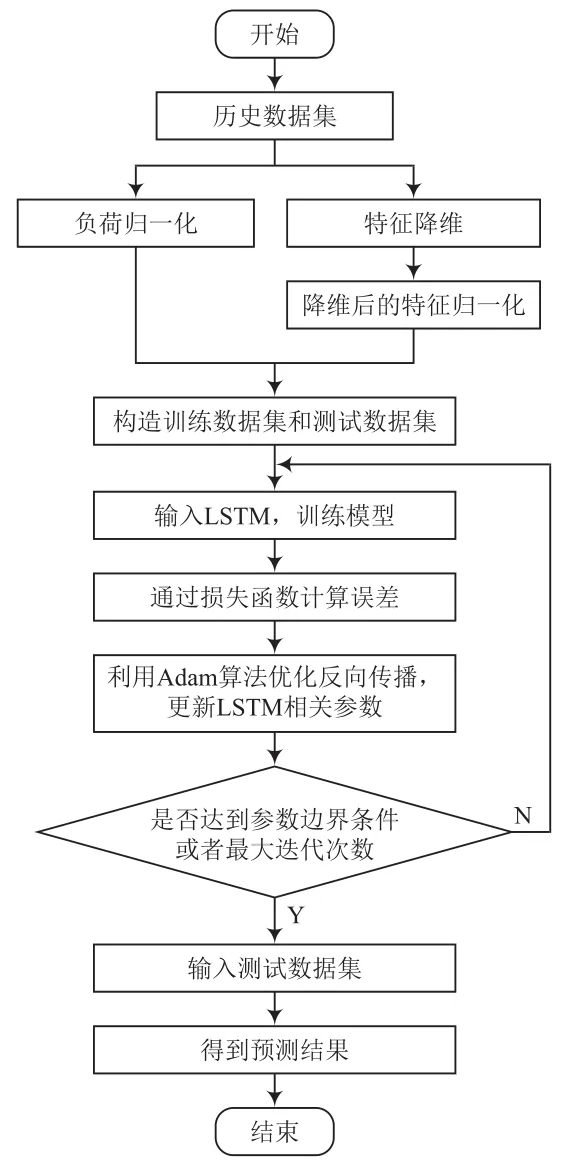
图2 基于PCA-LSTM的电力负荷预测建模流程
3.2 实验评价指标
为评估本文提出模型的精确度,采用平均绝对百分比误差(MAPE)、均方值误差(RMSE)、绝对百分比误差(APE)进行评估。按照国家电网公司的规定:当平均绝对百分比误差低于5%时,表示预测方法符合实际应用标准;平均绝对百分比误差低于3%时,表示预测方法性能良好;平均绝对百分比误差低于2%时,表示预测方法有效;平均绝对百分比误差低于1%时,表示预测方法具有较高的应用价值与精准度[13]。
(1)均方值误差(RMSE)

(2)平均绝对百分比误差(MAPE)

(3)绝对百分比误差(APE)

4 算例分析
4.1 实验环境配置
本 文 实 验 环 境 采 用 Intel(R)core(TM)i5-5200 CUP2.20-GHz处理器,8 GB内存。选用python3.7作为编程语言,软件构架基于Tensorflow框架。
4.2 数据来源
为验证模型的精确性,选择2016年电工数学建模竞赛负荷预测数据集,数据集包含某地区2012年1月1日到2015年1月10日总计1 106天的日负荷数据和气象数据,气象数据包括每日最高温度、最低温度、平均温度、相对湿度和降雨量。
4.3 数据预处理
历史负荷数据和气象数据由于数据采集器故障、数据遗漏等问题,存在异常值和缺失值,影响了模型的预测精度,因此需要对缺失值和异常值进行相关处理。将异常值与缺失值均视为缺失值进行处理,采用平均值法对缺失值进行填充[14]。将数据集中前1 076个负荷数据作为训练集,将后30个数据作为测试集。
4.4 对气象数据进行主成分提取
对5个负荷影响因素(最高温度、最低温度、平均温度、相对湿度、降雨量)进行主成分分析,得到5个指标变量[15]。5个指标变量的协方差矩阵特征值见表1所列。

表1 5个变量的协方差矩阵特征值
通常当累计方差贡献率达到75%~90%时,对应的前m个主成分就能够包含原始负荷影响数据中的大部分信息。设定方差累计贡献率的阈值为90%,由上表可知,前2个主成分已达到81.511%,后3个主成分可以作为噪声不予考虑。因此用2个主成分代替原始气象数据输入网络进行训练。
由于主成分分析后的2个主成分数值波动很大,不利于LSTM网络的训练,因此对2个主成分进行归一化处理,将主成分数值归一化0到1之间,防止LSTM网络中的激活函数出现饱和现象[16]。归一化公式:

式中:ug为归一化后的值;umin为数据集中的最小值;umax为数据集中的最大值;u为对应数据集中的值。
4.5 预测结果对比
为验证本文所提预测模型的精确性,分别使用只有负荷作为输入的单特征LSTM网络模型;气象因素和负荷作为输入的多特征LSTM网络模型;对气象因素进行主成分分析的LSTM网络模型(PCA-LSTM);气象因素和负荷作为输入的ANN网络模型。同时使用MAPE、RMSE评价各模型的预测效果,各模型预测误差对比见表2所列,实际和预测值及绝对百分比误差见表3所列。
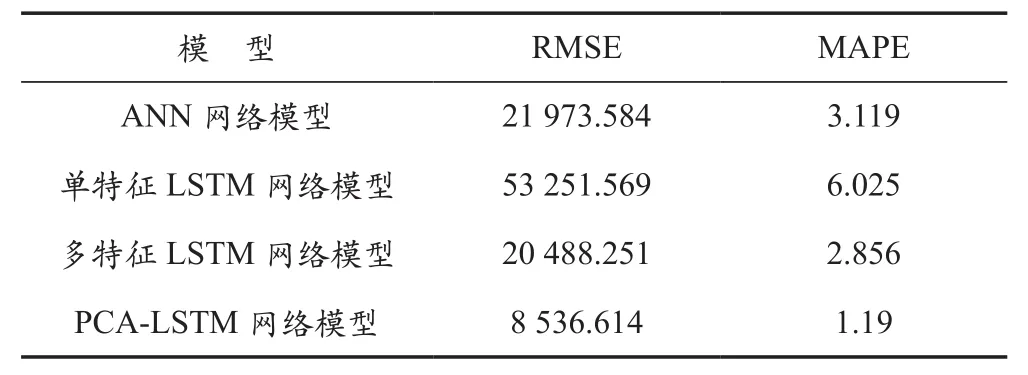
表2 4种模型的RMSE、MAPE对比
4种模型电力负荷预测的绝对百分比误差对比如图3所示,预测曲线与实际曲线对比如图4所示。
RMSE、MAPE值越小,说明该模型的预测效果越好。分析表2可知,单特征LSTM网络模型的RMSE、MAPE值均为最大,说明气象因素对电力负荷的预测结果影响巨大,在神经网络训练时加入气象因素作为输入值,可以大大提高电力负荷的预测精度。将ANN神经网络模型和多特征LSTM网络模型的RMSE、MAPE值进行对比,可以发现多特征LSTM网络模型优于ANN神经网络模型,在时间序列数据中,LSTM网络模型相比传统神经网络模型更优。将气象因素进行主成分分析并输入LSTM网络训练后,MAPE值相对ANN神经网络模型降低了1.929%,相对多特征LSTM网络模型降低了1.756%。
结合表3,PCA-LSTM网络模型的绝对百分比误差均在1左右波动,对测试集第22条数据进行预测时,由于数据波动较大,ANN神经网络模型、单特征LSTM网络模型、多特征LSTM网络模型、PCA-LSTM网络模型的绝对百分比误差分别为23.831,77,19.928,5.151。结合图3可以得出,PCA-LSTM网络模型在电力负荷预测优越性和坚挺性,特别是负荷数据产生巨大变化时依然可以较为准确的预测负荷,该模型相对其他模型鲁棒性较强。通过图4可以看出,PCALSTM网络模型的预测效果优于其他预测模型。

图3 4种模型的绝对百分比误差对比图

图4 预测曲线与实际曲线对比图

表3 实际和预测值及绝对百分比误差
5 结 语
本文提出了一种基于PCA-LSTM网络的负荷预测模型,采用PCA方法对每日气象数据进行数据降维,构建LSTM网络模型,通过对数据的仿真建模验证本文提出的PCALSTM,得到如下结论:
(1)通过单特征LSTM网络、多特征LSTM网络、PCA-LSTM网络的对比可以发现,气象因素对负荷预测的影响巨大,加入气象因素的网络可以提高其预测精度;通过对气象因素降维不仅保留了数据的大部分信息,还去除了数据中的噪声,提高了模型的预测精确度。
(2)LSTM网络模型可以利用时间序列有效分析时序性数据中的隐含信息,通过PCA-LSTM网络与ANN网络的对比可知,提出的模型可以获得更高的预测精度,应用潜力更大。
