基于下垂控制的并联逆变器间环流控制策略

2021-08-25吴海洋赵兴勇

自动化与仪表 2021年8期

吴海洋，赵兴勇，郭垚

（山西大学电力与建筑学院，太原030013）

近年来，随着分布式发电技术发展和广泛使用，微网系统成为当今研究的热点话题[1]，逆变器是微电网系统的核心单元，因此也受到了广泛关注[2]。单台逆变器由于无法满足大电网的需求，现多为逆变器并联运行的情况。但是在实际应用中，各分布式电源的地理位置具有差异性，使得连接逆变器的线路阻抗不尽相同，产生不相同的压降，从而在各逆变器之间产生不同程度的环流。环流导致并网电流严重畸变，损耗增加，系统效率降低，导致逆变器损坏，甚至大电网崩溃[3-4]。所以，为了微网可以稳定高效运行，必须解决并联逆变器之间的环流问题[5]。

目前，并联逆变器的运行控制技术可以根据通信线的有无分为两类，即互连线控制和非互连线控制方法。有互联线控制方式均流精度高，但是通信复杂，互连线的存在受地理位置的限制，可靠性较低。以下垂控制为核心的无互联线控制模式可以灵活配置系统单元，实现微电网中各微源的协调输出和输出功率的合理分配[6]，使其具有良好的冗余性，因此在实际中得到了广泛的应用。传统下垂控制实现方法简单，但控制精度不够高，微源逆变器受自身输出阻抗和线路阻抗的影响，输出有功功率和无功功率相互耦合。并且等效连线阻抗之间的差异性会造成微源逆变器之间环流的增大。

针对以上问题，现大多数都是采用基于虚拟阻抗的下垂控制技术，即在传统下垂控制中，引入已经设计好的虚拟阻抗来重塑逆变器的输出阻抗，使得逆变器并联支路的等效连线阻抗之间能够互相匹配，减少功率之间的相互耦合，从而有效地抑制了环流。文献[7-9]中虚拟阻抗的引入改善了线路阻抗的特性，解决了系统输出功率耦合的问题，但虚拟阻抗的引入会降低公共母线电压；文献[10]采用一种改进下垂控制与虚拟电抗相结合的控制方法实现了有功与无功的解耦，但该方法的精度不高；文献[11]使用串联虚拟电容器方法使系统等效连线阻抗被设计为容性的，从而改善了由无功功率变化引起的逆变器输出电压降的问题；文献[12]分析了微电网并联逆变器环流产生的根本原因，从减小输出电压偏差和等效连接阻抗差两个方面提出了一种改进的下垂控制方法来抑制环流；文献[13]通过引入复合型虚拟阻抗将等效连线阻抗设计成感性来实现功率解耦，而后改进了下垂控制环节提高无功功率均分来抑制环流。

为了解决微电网孤岛运行时并联逆变器系统线路阻抗参数不一致造成的环流问题，本文提出了一种改进的下垂控制策略，通过引入虚拟电容来解决线路阻抗差异的影响以及输出电压跌落的问题，然后通过在下垂控制中改进无功环节提高无功功率均分精度，从而抑制环流。通过仿真验证该方法的可行性和实用性。

1 并联逆变器的功率特性和环流特性

1.1 传统下垂控制的功率特性

微电网两并联逆变器等效模型，如图1所示。

图1 微电网两并联逆变器模型Fig.1 Model of two parallel inverters in microgrid

其中Udcn（n=1，2）为分布式电源；逆变器1 和逆变器2 的输出电压是Un（n=1，2）；电感Ln（n=1，2）以及电容Cn（n=1，2）对系统产生的高频次谐波进行滤除；ZLinen（n=1，2）是将逆变器连接到公共交流母线的线路的阻抗；ZLoad为公共负载，负载电压为UL。

忽略逆变器输出阻抗，根据图1可以得到逆变器i（i=1，2）的输出功率方程为

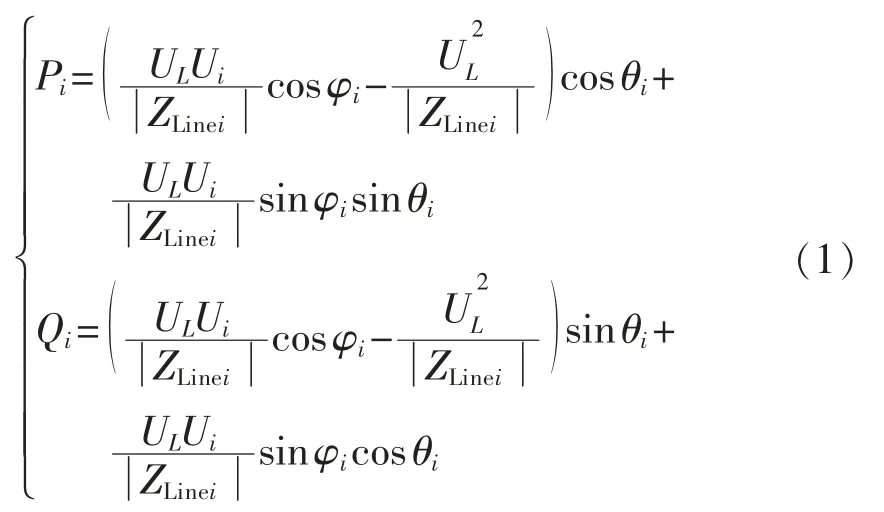
在高压微电网中，Xi≫Ri，同时由于ϕ 在实际中很小，所以认为

因此，可得此时逆变器i（i=1，2）的输出功率方程为

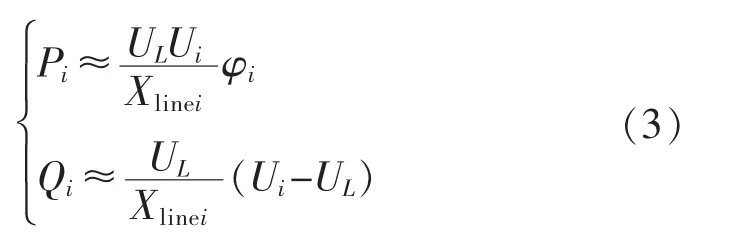
已知相角与频率、角速度的关系为

所以，传统的下垂控制表达式为

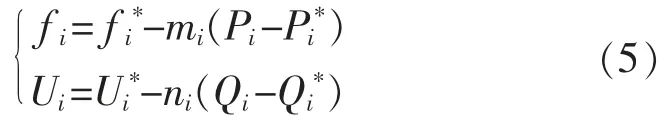
式中：fi*，Ui*，Pi*，Qi*分别为逆变器输出的额定频率与额定电压、输出的额定有功功率与额定无功功率；mi，ni分别为有功下垂控制系数与无功下垂控制系数；Pi，Qi为逆变器实际输出的有功与无功功率。

1.2 并联逆变器等效电路模型及环流分析

本文建立了两个相同容量逆变器的等效电路模型，拓扑结构如图2所示。

图2 微电网两并联逆变器等效电路模型Fig.2 Equivalent circuit model of two parallel inverters in microgrid

其中，逆变器的输出电压表示为Un（n=1，2）；负载端电压为UL和负载阻抗为ZLoad，这里设定电压相位为0；Rn（n=1，2）和Xn（n=1，2）分别表示连线电阻和连线电抗；Zn（n=1，2）表示逆变器1，2 的等效连线阻抗，则：

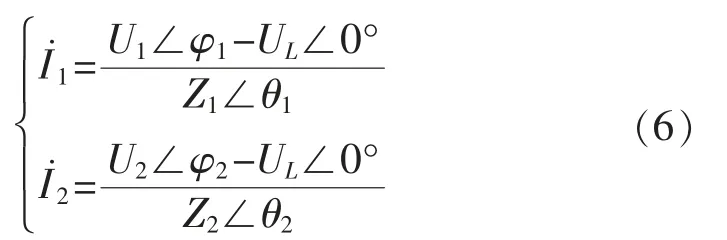
由此可得环流公式为

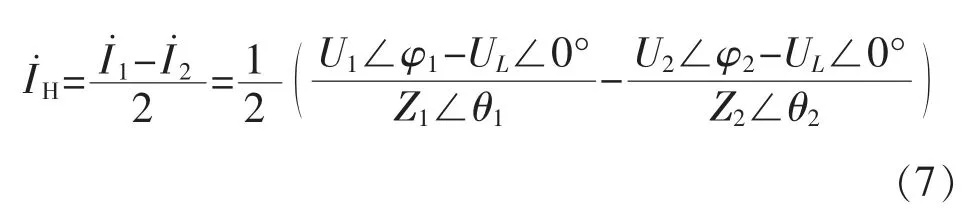
由于两个逆变器参数完全相同并且容量相同，根据式（6）和式（7）可知，在等效连线阻抗完全一致时，系统中没有环流。但是在实际应用中，由于每个分布式电源的地理位置不同，使得连接逆变器的线路长度也不相同，导致等效连线阻抗不一致，逆变器间就会有环流产生。

1.3 并联逆变器间环流与功率均分关系

并联逆变器等效电路简化模型如图3所示。

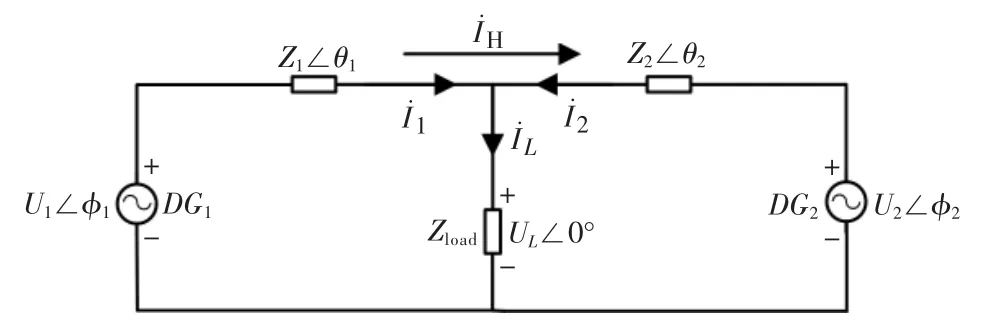
图3 并联逆变器等效电路简化模型Fig.3 Simplified model of equivalent circuit of parallel inverter

在图3中，假设Z1∠θ1＝Z2∠θ2＝Z∠θ，两逆变器间的环流可以写成另一种形式：

将公式（8）标准化，并考虑按逆变器容量来分配负载电流，对于N 台系统并联，则第i（i=1，2，…，N）台逆变器的环流可表示为

式中：Ci表示第i 台逆变器容量在总系统容量中的占比，根据公式（9）可进一步得环流和功率的关系。当第i 台逆变器的环流为0 时，可得：

式中：PL，QL分别表示负载有功和无功功率。由式（10）可知，可以通过控制逆变器按容量对负载功率进行精确均分来消除并联系统间的环流。所以本文沿着这个思路对逆变器控制策略进行改进，实现更加精确的均分效果，从而到达更好抑制环流的目的。

2 基于下垂控制并联逆变器环流控制策略

2.1 引入虚拟电容

在逆变器传统的控制环中引入虚拟电容可使并联支路的等效连线阻抗相匹配，更好的实现功率之间的解耦。控制框图如图4所示。

图4 引入虚拟电容的逆变器控制框图Fig.4 Inverter control block diagram with the introduction of virtual capacitors

其中外环是电压环，内环为电流环。电压外环的比例系数与积分系数为kuP，kuI；kiP为电流内环的比例系数；kPWM为基波放大系数；u0为输出电压；uref为逆变器参考电压；Zv（s）为引入的虚拟电容；为增加虚拟电容后的参考电压值。

（1）在不加虚拟电容的情况下，系统的传递函数为

定义：

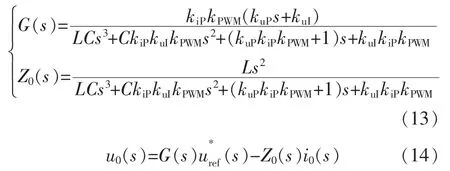
式中：G（s）为开环传递函数；Z0（s）为未加入虚拟电容前逆变器等效连线阻抗。

（2）在加入虚拟电容的情况下：

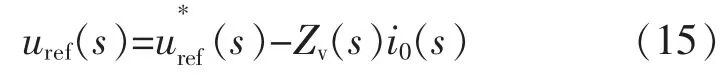
将式（15）带入式（11）可得：

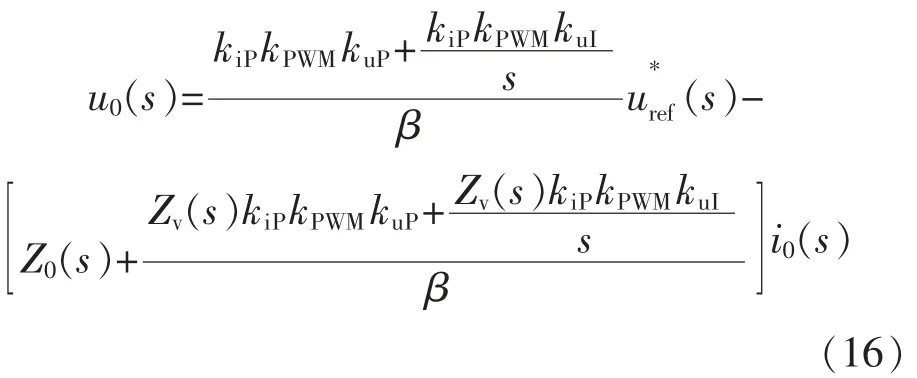
式中：

则传递函数可简写为

定义：

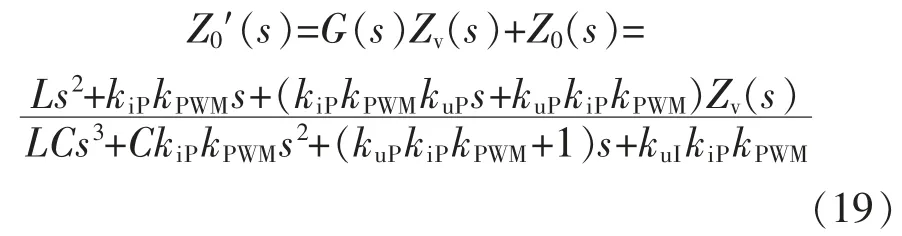
式中：Z0′（s）是引入虚拟电容后逆变器等效连线阻抗。引入的虚拟阻抗为

式中：Cv为虚拟电容。引入虚拟电容前后逆变器等效连线阻抗幅频特性曲线对比如图5所示。

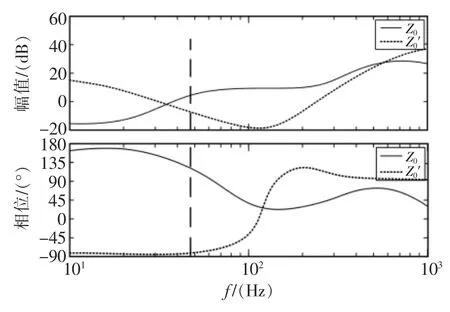
图5 引入虚拟电容后的等效连线阻抗伯德图Fig.5 Bode diagram of equivalent connection impedance after introducing virtual capacitor

从图5中可知，工频条件下加入虚拟电容后，系统的等效连线阻抗呈现容性，降低了系统的功率耦合度，实现了系统有功功率与无功功率的解耦，从而易于功率之间的均分。

2.2 改进下垂控制器

在传统下垂控制中引入虚拟电容可以在一定程度上降低并联逆变器之间的环流，实现功率解耦，但不能达到真正令人满意的均分效果。为了实现更精确的功率分配和消除环流，提出了一种改进的下垂控制策略。

首先，线路上的压降为

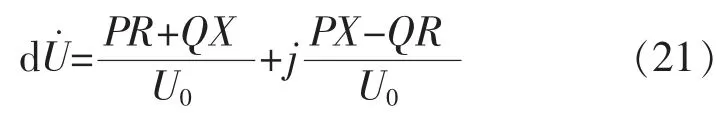
因虚拟电容的引入，可认为线路阻抗呈现容性，阻性成分忽略不计，则：

令其中：

可得：

式中：U0为负载电压；Xi为线路的电抗值。然后作出线路阻抗差异引起的无功均分误差，如图6所示。

图6 线路阻抗差异引起的无功均分误差Fig.6 Diagram of reactive power sharing error caused by line impedance difference

图6中两并联逆变器采用相同的下垂控制系数n，线路1 电抗为X1，线路2 电抗为X2，并设X1＞X2，则根据式（23）可得k1＞k2，交下垂曲线于a，b 两点，对应的输出电压分别为U1，U2，输出无功功率分别为Q1，Q2。从图中可知，Q1＜Q2，两条支路输出的无功功率不相同，未达到功率均分的效果。

现对传统的下垂控制方程作以改进，改进后两并联逆变器输出无功均分示意图如图7所示。

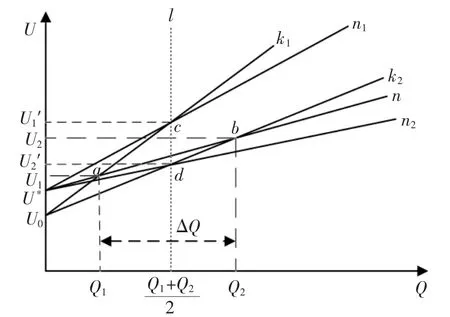
图7 改进后两并联逆变器输出无功均分示意图Fig.7 Schematic diagram of improved reactive power sharing of output of two parallel inverters

改进后的下垂控制表达式为

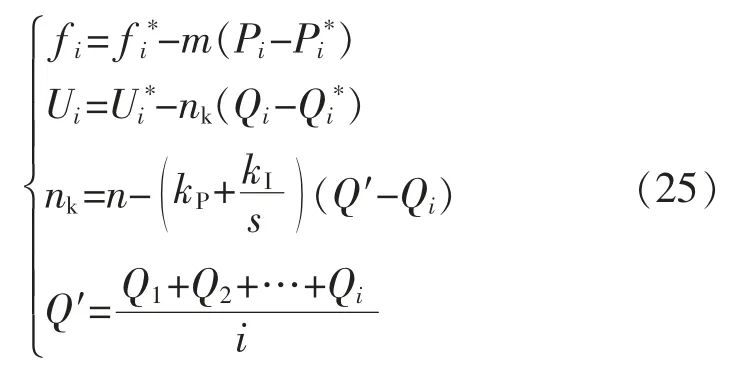
式中：nk是经改进后的逆变器无功下垂系数；kP，kI分别为引入PI 控制器的比例系数和积分系数；Q′为各逆变器无功功率控制给定值；i 为逆变器并联个数。此方法可以动态跟踪各分支无功功率的变化来对各分支的无功输出进行实时调整，实现更加精确的无功均分，消除无功环流。基于改进后的下垂控制框图如图8所示。

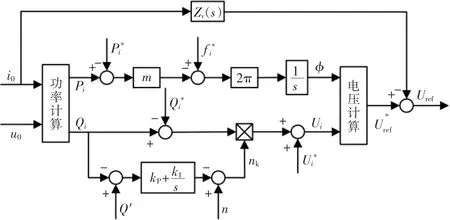
图8 改进后的下垂控制框图Fig.8 Improved droop control block diagram

3 仿真分析

为了验证控制策略的正确性和有效性，在MATLAB/SIMULINK 仿真实验平台上，根据图1建立了不同线路阻抗条件下两个相同容量逆变器并联系统的仿真模型，具体参数如表1所示。不同控制策略下并联系统有功功率均分效果如图9所示。

表1 系统的主要参数Tab.1 Main parameters of system

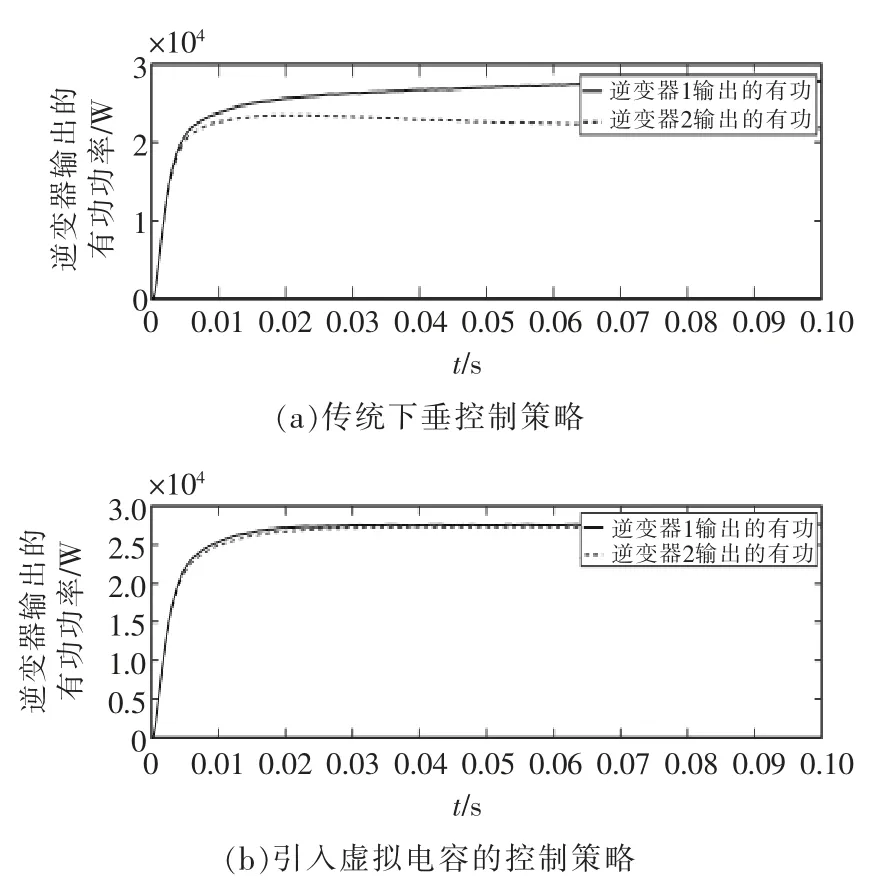
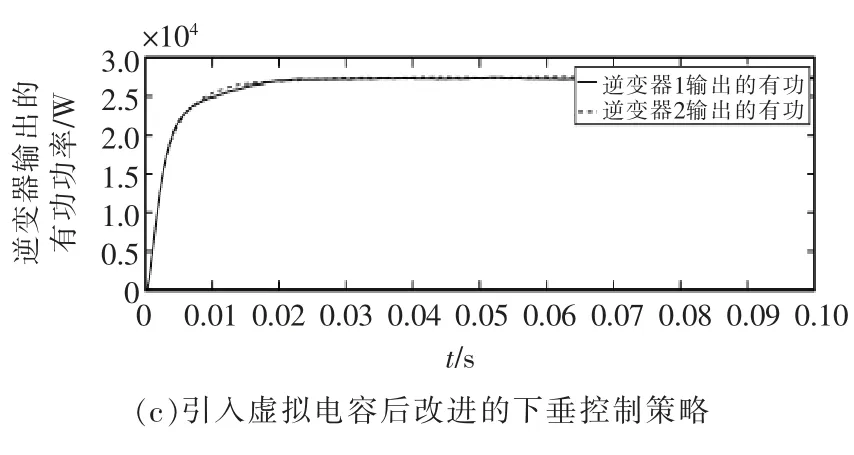
图9 不同控制策略下并联系统有功功率均分效果Fig.9 Effect diagram of active power sharing of parallel system under different control strategies

从图9可知，在连线阻抗不一致的条件下，系统采用传统的下垂控制策略时，有功功率并未达到均分效果，在0.1 s 时有功功率相差6000 W；而采用后两种控制策略时，由于引入虚拟电容使有功和无功解耦，提高了功率均分精度，两个逆变器的有功功率输出经过短时间的波动后迅速达到稳定状态，有功实现了均分，逆变器1 和逆变器2 输出的有功功率为27000 W。

不同控制策略下并联系统无功功率均分效果如图10所示。

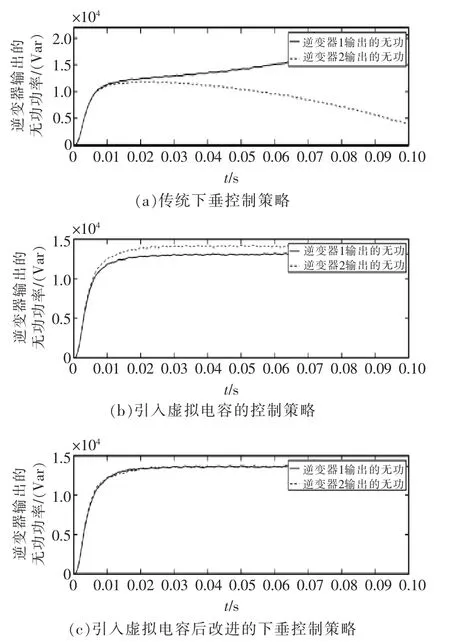
图10 不同控制策略下并联系统无功功率均分效果Fig.10 Reactive power sharing effect diagram of parallel system under different control strategies

从图10可知，采用传统的下垂控制策略0.1 s时无功功率已相差20000 Var；而采用引入虚拟电容的控制策略时，两逆变器输出的无功经过短暂的波动后都实现了稳定输出，逆变器1 和逆变器2 输出的无功分别为13000 Var 和14000 Var，相比而言该控制策略对于无功均分已有了显著改善，但并未实现满意的均分效果；采用引入虚拟电容后改进的下垂控制策略时，由于对下垂控制中无功控制环节进行改进，所以得到了更加精确的均分效果，两逆变器输出的无功功率在短暂的小波动之后，稳定的输出无功13800 Var。

不同控制策略下两逆变器间环流抑制效果对比如图11所示。

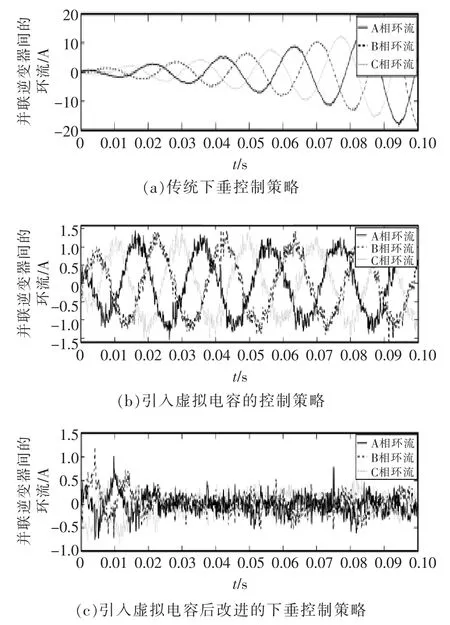
图11 不同控制策略下两逆变器间环流抑制效果对比Fig.11 Comparison of circulating current suppression effects between two inverters under different control strategies

从图11中可以看到，采用传统下垂控制策略时，有功与无功的耦合程度高，两并联逆变器间存在较大的环流；引入虚拟电容后，减小了等效输出阻抗差异，使功率间解耦，并提高了系统的功率均分精度，因此很大程度抑制了环流，使环流幅值稳定在了1.5 A；而引入虚拟电容后，通过改进下垂控制策略中的无功控制环节，使输出的无功达到更加精确的均分，因此环流抑制效果更显著，环流幅值控制在了0.8 A。

不同控制策略下输出电压有效值波形如图12所示。

图12 不同控制策略下输出电压有效值波形图Fig.12 Waveform diagram of effective value of output voltage under different control strategies

传统下垂控制策略中，随着逆变器输出无功的增加，其输出电压将降低，这将导致公共母线电压严重下降。本次仿真设置的交流母线电压参考值为380 V，采用传统的下垂控制策略后，A 相瞬时输出电压峰值为332 V，电压偏差为1.6%；而引入虚拟电容后，使传统感性下垂控制变为容性条件下的下垂控制，采用引入虚拟电容的控制策略，在负载电压满足需求的同时兼顾着改善母线电压偏移的作用，A 相瞬时输出电压峰值为340 V，相比于传统的下垂控制策略，增长了2.5%，电压偏差为0.9%。所以，采用引入虚拟电容后改进的下垂控制策略可以更好的抑制并联逆变器间的环流，同时也起到了改善交流母线电压偏移的作用。