对第33届全国中学生物理竞赛复赛第6题的解答的质疑
2021-08-25范雪娇
李 惠 范雪娇
(株洲市第二中学 湖南 株洲 412007)
【原题】(节选)光电倍增管是用来将光信号转化为电信号并加以放大的装置,其结构如图1所示.它主要由一个光阴极、n个倍增极和一个阳极构成;光阴极与第1倍增极、各相邻倍增极及第n倍增极与阳极之间均有电势差V;从光阴极逸出的电子称为光电子,其中大部分(百分比η)被收集到第1倍增极上,余下的被直接收集到阳极上;每个被收集到第i倍增极(i=1,…,n)的电子在该电极上又使得δ个电子(δ>1)逸出;第i倍增极上逸出的电子有大部分(百分比σ)被第i+1倍增极收集,其他被阳极收集;直至所有电子被阳极收集,实现信号放大.已知电子电荷量绝对值为e.求:光电倍增管放大一个光电子的平均耗能,已知δσ>1,n>1.
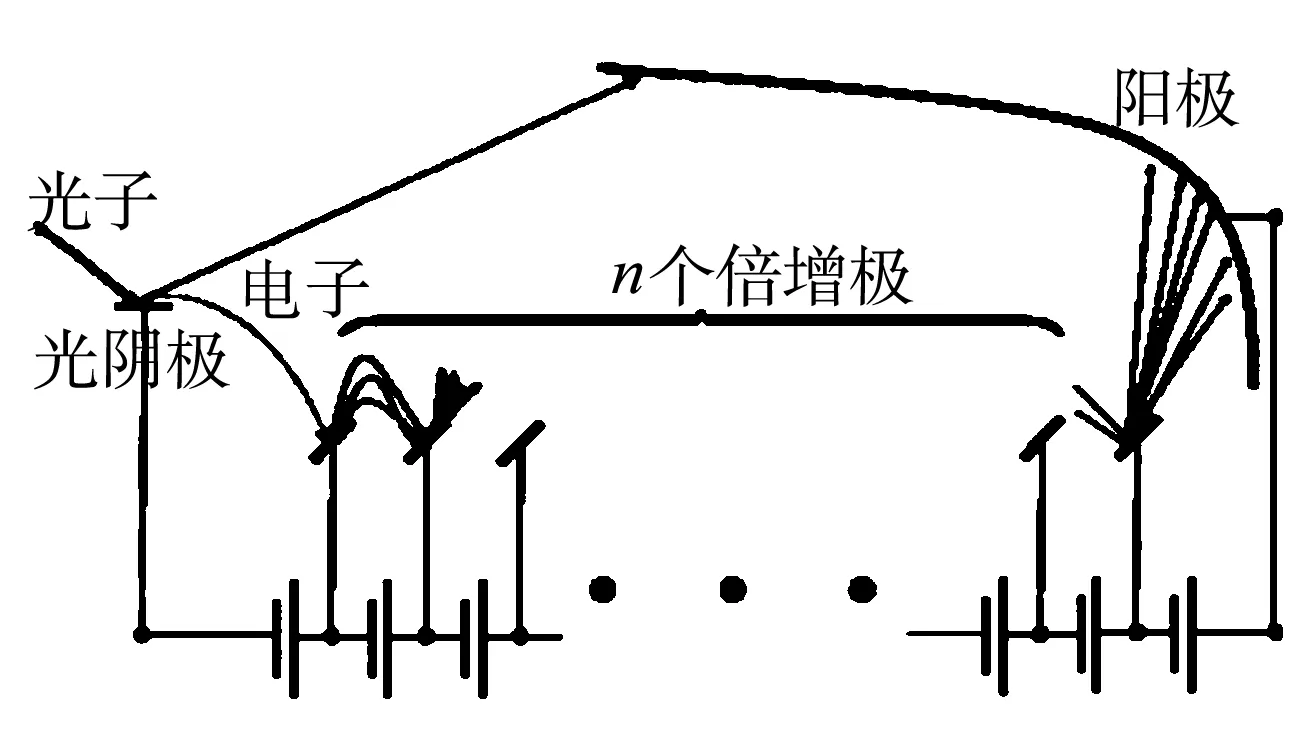
图1 光电倍增管结构图
原题一共有2小问,笔者只节选了参考解答有误的第1小问,附上其解答结果.
光电倍增管放大一个光电子的平均耗能为
式中np是从光阴极逸出的电子个数,E是消耗的总电能.
1 对结果的质疑及验证

我们把n=0代入原解答得
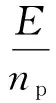
(1)
显然不正确.
进一步验证n=1的情形.当n=1时,其物理意义是光电倍增管中有np个光电子从光阴极逸出,有ηnp个光电子被收集到第1倍增极上,(1-η)np个光电子被直接收集到阳极上,最后有δηnp个光电子从第1倍增极上逸出,被收集到阳极上.我们分成两步来计算光电倍增管放大以上这些光电子所消耗的电能.第一步,先计算从光阴极直接被阳极收集的光电子所消耗的电能.从光阴极到阳极的电势差为
Vpa=(n+1)V=2V
(2)
一共有(1-η)np个光电子从光阴极到阳极,一共消耗的电能为E1,有
E1=2(1-η)npeV
(3)
第二步,计算从光阴极逸出被第1倍增极收集再从第1倍增极被阳极收集的光电子消耗的电能E2,显然
E2=(η+ηδ)npeV
(4)
最后,把两部分消耗的电能加起来,求得
E=E1+E2
(5)
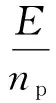
(6)
那么,把n=1代入原参考解答,会是这个结果吗?
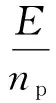
(7)
显然,代入之后的结果式(7)与真实物理意义对应下的结果式(6)不符.
结论:原解答有误.
2 笔者所做的详细解答及验证
为了能让读者清晰地看到加速各部分光电子所消耗的电能,笔者先进行简单的罗列如下:
放大从光阴极到第1倍增极,和光阴极到阳极的光电子消耗的电能为E0,有
E0=[η+(1-η)(n+1)]npeV
(8)
放大从第1倍增极到第2倍增极,和第1倍增极到阳极的光电子消耗的电能为E1,有
E1=[ηδσ+ηδ(1-σ)n]npeV
(9)
放大从第2倍增极到第3倍增极,和第2倍增极到阳极的光电子消耗的电能为E2,有
E2=[ηδ2σ2+ηδ2σ(1-σ)(n-1)]npeV
(10)
放大从第3倍增极到第4倍增极,和第3倍增极到阳极的光电子消耗的电能为E3,有
E3=[ηδ3σ3+ηδ3σ2(1-σ)(n-2)]npeV
(11)
放大从第(n-1)倍增极到第n倍增极,和第(n-1)倍增极到阳极的光电子消耗的电能为En-1,有
En-1=[ηδn-1σn-1+2ηδn-1σn-2(1-σ)]npeV
(12)
放大从第n倍增极到阳极的光电子消耗的电能为En,有
En=(ηδnσn-1)npeV
(13)
接下来,把式(8)~(13)相加得
E=E0+E1+E2+…+En-1+En
(14)
在式(14)等号右边含有两个等比数列,其一是ηnpeV,ηδσnpeV,ηδ2σ2npeV,…,ηδn-1σn-1npeV,我们用级数S1来表示上述等比数列的和;其二是ηδ·(1-σ)nnpeV,ηδ2σ(1-σ)(n-1)npeV,ηδ3σ2(1-σ)·(n-2)npeV,…, 2ηδn-1σn-2(1-σ)npeV,我们用级数S2来表示上述等比数列的和;还剩下两项(1-η)·(n+1)npeV+ηδnσn-1npeV作为第3部分.现在我们来求以上3部分的和.
显然
(15)
S2=ηδ(1-σ)npeV[n+δσ(n-1)+δ2σ2n-2+…+δn-2σn-2·2)]
(16)
构建级数S3=δσS2来错位求和
S3=ηδ(1-σ)npeV[δσn++δ2σ2(n-1)+…+δn-2σn-2·3+δn-1σn-1·2)]
(17)
式(16)、(17)相减得
(18)
把以上3部分相加得
E=E1+E1+E2+…+En-1+En=
S1+S2+(1-η)(n+1)npeV+ηδnσn-1npeV=
(1-η)(n+1)+ηδnσn-1}npeV
(19)
于是光电倍增管放大一个光电子的平均能耗为
(1-η)(n+1)+ηδnσn-1}eV
(20)
我们将n=1代入式(20)中,进行验证
(1-η)(1+1)+ηδ1σ0}eV=
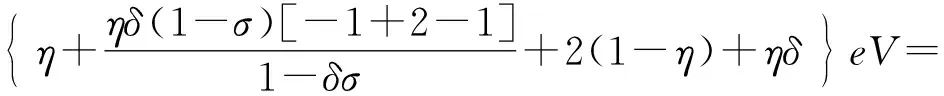
(21)
与式(6)比较,完全吻合.
我们再把文首的n=0的情况代入式(20)中得
(1-η)+ησ-1}eV=
结果与实际的物理意义完全吻合.
综上所述,式(20)才是本题的正确解答,原解答确实有误.
