带电粒子在偏转电场运动过程中的能量转化与守恒分析
2021-08-25陈曦
陈 曦
(中国人民大学附属中学 北京 100080)
张石友 张晓琳
(北京市第一七一中学 北京 100013)
在带领学生进行高三复习时,遇到了一道看似平常的练习题,“奇怪”的是:从两个不同的角度求解,得到的“答案”却不同,引发了我们的思考与讨论,问题描述如下.
【例题】两个平行且彼此靠近的金属板与一直流电源两极相连,电源的内阻可忽略不计,两板间形成的电场可认为是匀强电场.有质量为m,电荷量为-q的粒子,不间断地从两平行板左侧中点以初速度v0沿垂直场强的方向射入电场,粒子偏转后恰打在下极板的边缘上,如图1所示.已知单位时间入射的粒子数为n,两平行板的间距为d,金属板长度为L,不计粒子重力.求稳定时电源的输出功率.
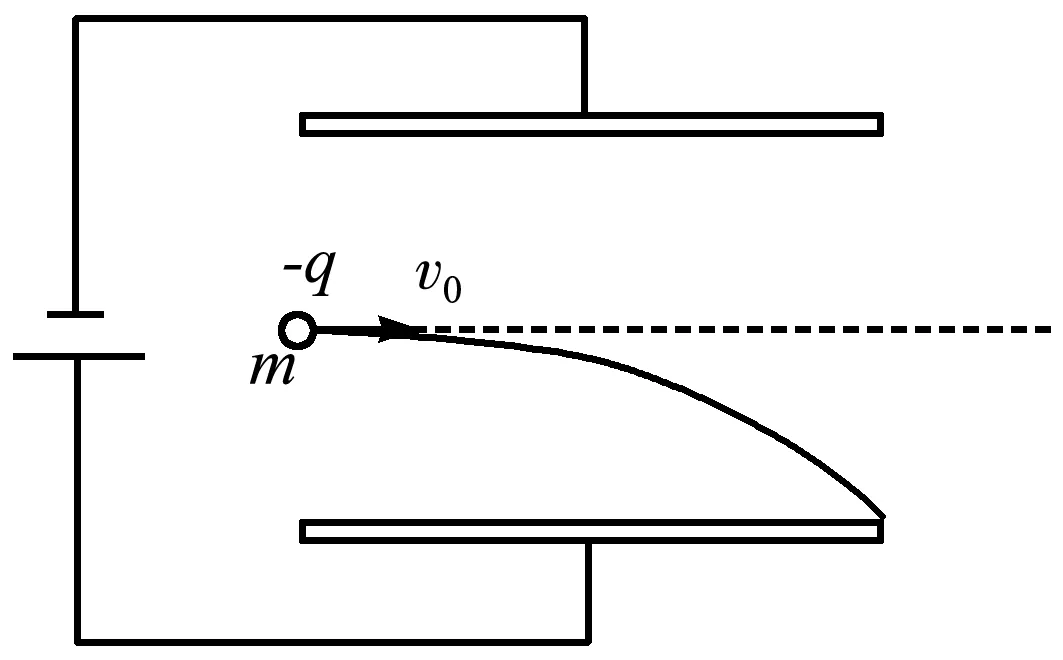
图1 单个粒子打在极板的边缘
解法1(参考答案):
解析:粒子打在极板上,电路导通,电流
(1)
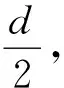
(2)
由式(1)、(2),可得电源输出功率
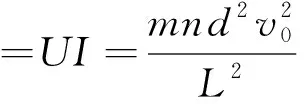
解法2(从能量转化与守恒的大思路来展开):
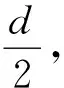
(3)
对单个粒子来说,电源做的功即增加的动能为
(4)
单位时间内电源对粒子所做的功,为
W=nW0
(5)
由式(3)、(4)、(5),可得电源输出的功率
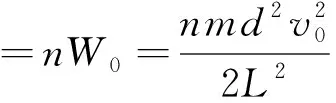
上述两种方法中,一个认为回路中的电流是因为有带电粒子打到极板上产生的;另一个则是避开电流的问题,直接利用能量守恒求解.孰对孰错?
为了弄清楚这个问题,我们不妨做个假设:假如没有带电粒子打到极板上,如图2所示.按照“参考答案”所给思路,电路中就会没有电流,电源的输出功率也将是零,那么带电粒子偏转后获得的动能哪里来的?岂不违背能量守恒定律嘛!据此我们可以判定,第一种求解方法应该是存在问题的.
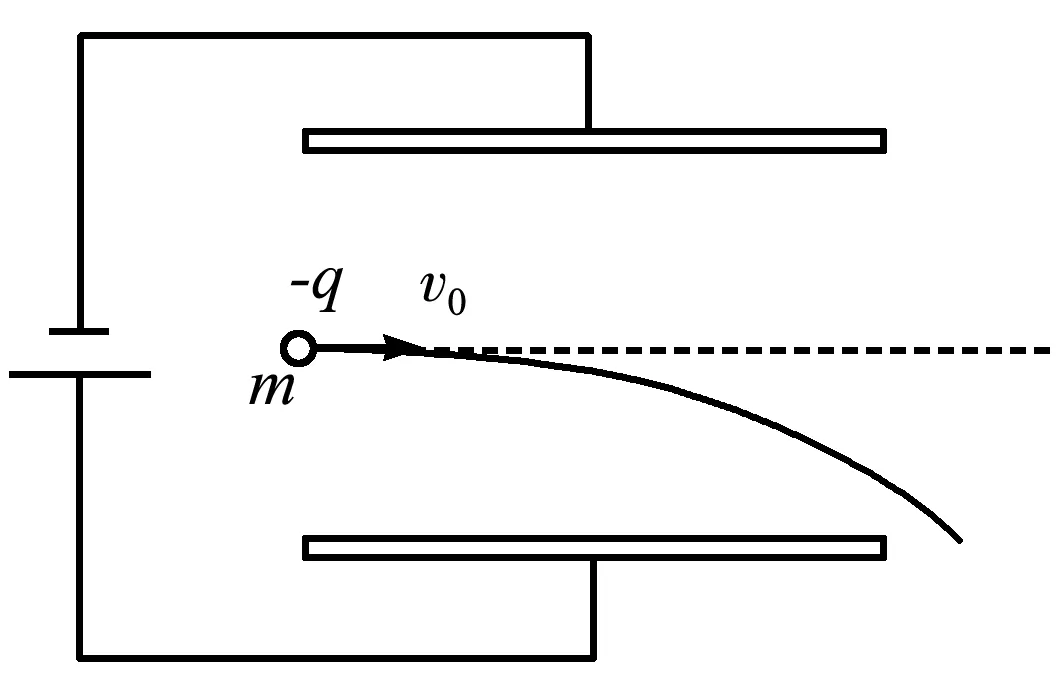
图2 单个粒子从极板间射出
经查阅资料并讨论交流后发现:带电粒子(-q)在进入平行板电容器后会引起两板发生静电感应现象,在上下两个极板上都感应出电荷,感应电荷的电量和带电粒子与极板的距离有关.偏转过程中,带电粒子和两个极板的距离发生变化,导致两个极板上感应电荷的电量也发生变化.一部分感应电荷沿着外电路从一个极板流向另一个极板,形成电流.因此我们并不能认为只有带电粒子打到极板上一瞬间,外电路中才会有电流,更不能认为电流的大小等于单位时间内打到极板上的电荷量.电流流过电源时,电动势做功将其他形式的能转化为电能和带电粒子的动能.
为了能在高中或者高中物理竞赛的知识范围内计算感应电荷的电荷量,我们做以下两个近似.第一,带电粒子入射之前,只有两极板之间存在匀强电场,空间其他位置处没有电场.第二,入射带电粒子的电量远小于电容器所带电量,带电粒子入射之后,除带电粒子周围,两极板之间的大部分区域内的电场仍然可以近似看作匀强电场.在这两个近似下,我们能得到两个结论.首先,利用高斯定理可以证明两个极板上产生的感应电荷总量保持为+q.其次,利用电势叠加[1]和高斯定理[2],可以证明两极板上感应电荷的电量之比等于两极板和带电粒子距离的反比.篇幅所限,我们将在后续的论文中进一步讨论计算感应电荷的方法,并证明上述两个结论.
具体举例说明如下.
说明1:带电粒子偏出电场
设单位时间内有n个带电粒子进入偏转电场并发生偏转,如图3所示.仅考虑进入电容器之间的带电粒子引起两极板发生静电感应而产生感应电荷,整个“弧形带电粒子流”在平行板电容器之间是稳定存在的,因此引起两极板的感应电荷分布也是稳定的,因此只需考虑单位时间内“新进入”和“刚飞出”的带电粒子即可,考虑到整个过程是持续稳定的过程,因此可以等效视为每1 s内都有-nq的电荷量进入,也有-nq的电荷“飞出”.事实上,为了弄清楚电路电流情况,我们只需考虑每秒内两极板上因上述“飞入”和“飞出”的-nq电荷量引起的极板上感应电荷量变化即可,这个过程中电源负责搬运的电荷量也恰好是这个数值,这个电荷量与电路中的电流相对应.
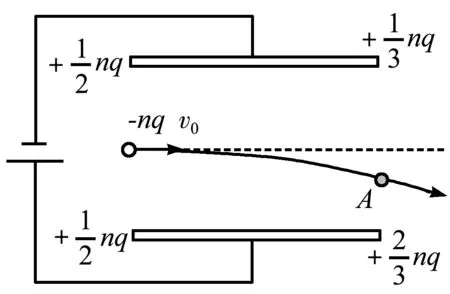
图3 多个粒子从极板间射出
上极板感应电荷量变化为
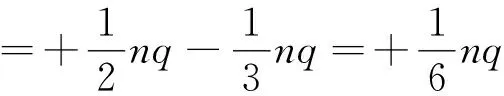
下极板感应电荷量变化为
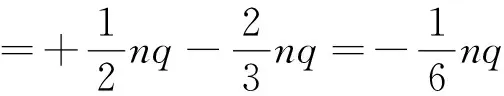
如果要维持系统稳定,极板上的电荷量应稳定不变,这就需要电源把上极板多出的电荷搬运到下极板.即:回路中的电流大小为
说明2:粒子未偏出电场,最终打在下极板上
我们回到初始的题目,带电粒子恰好打到下极板边缘(图4).若带电粒子打在极板上作为末态.沿用上述说明1中的思路,可以得出下面的结论:
这里面要注意每秒内打在下极板的电荷量-nq会使得下极板电荷变化,同时因这部分电荷打在了下极板而使上极板上的感应电荷消失.这样总的来看:
上极板每秒内感应电荷量增加为
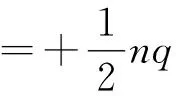
下极板感应电荷量增加量与打在下极板引起电荷变化的总和为
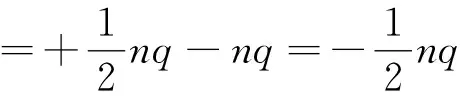
按照上述理论,回路中的电流大小应为
电源的输出功率为
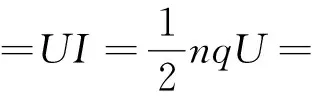
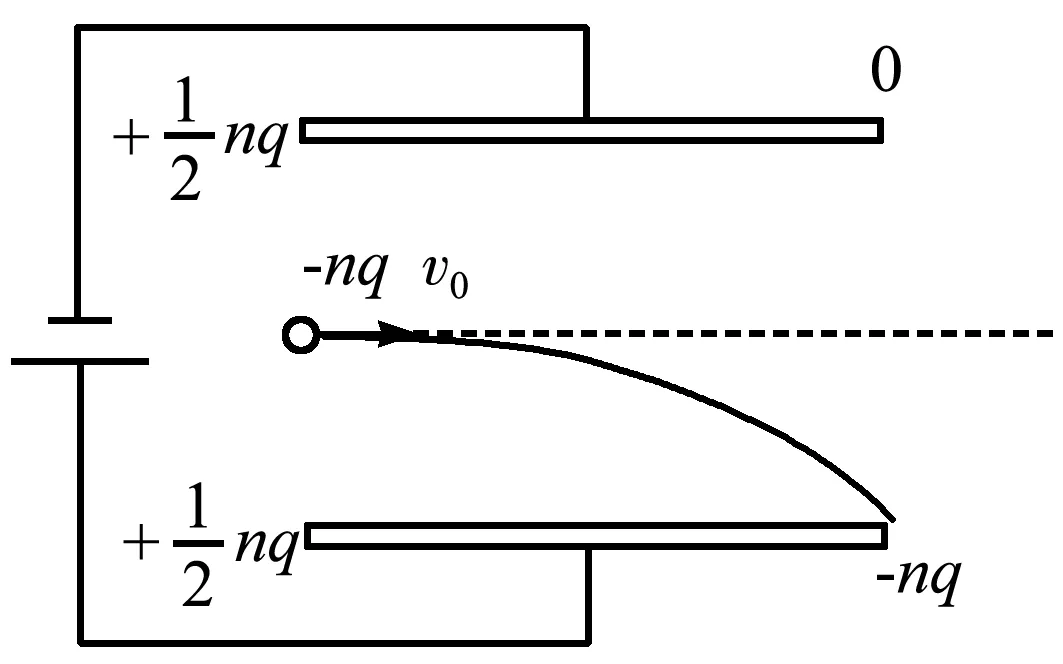
图4 多个粒子打在下极板边缘
当然了,尽管这种算法也能得到答案,但是笔者依然建议从能量转化与守恒的角度来分析问题.
综上所述,问题核心在于由于进入平行板电容器的并不是“等离子体”,这样使得通过电路的电荷量不是打在极板上的“电荷”量.在带电粒子不断靠近极板时,极板上感应电荷发生变化,为形成稳定的状态,电源会不间断地把多出的电荷从一个极板挪到另一个极板上,从而在回路中形成电流.
但也要注意到,上面的讨论也存在一定的局限性.考虑这样一种情况:电容器两极板带等量异号的电荷,和电源断开,如图5所示.带电粒子沿着虚线方向从无穷远处射入电容器,偏转之后离开电容器再运动至无穷远处.这个系统的能量包含3部分,带电粒子的电势能、电容器的电势能和带电粒子的动能.带电粒子从无穷远处来,又运动到无穷远处,它的电势能不变.电容器的电荷量不变,电势能也不变.带电粒子在电容器中被偏转电压加速,动能增加.综上所述,系统的总能量是增加的.在没有电源供电的情况下,系统增加的那部分能量是从哪里来呢?是否能量不守恒了呢?
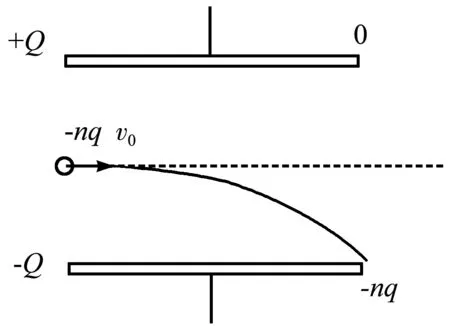
图5 多个粒子的电偏转
实际上,“忽略边缘效应”这一错误近似导致了“能量不守恒”这一似是而非的结果.高中阶段,我们通常认为只有电容器的两极板之间存在电场.而实际情况是,为了保证静电场做功和路径无关,电容器的外部也必然存在电场,我们将这种现象称为边缘效应.带电粒子穿过电容器两极板之间时被电场力加速,电势能转化为动能;带电粒子穿出电容器后,边缘效应又会对带电粒子减速,使其动能又重新转化为电势能.当带电粒子回到无穷远处时,它的动能和电势能都会回到其从无穷远出发时的数值,系统总能量守恒.
这些例子告诉我们,在高中物理范围内分析带电粒子在电场中的偏转时,模型本身的局限性可能会导致某些荒谬的结论.在日常教学中应加以重视,引导学生们通过推理论证,认识物理模型的局限性,加深对能量、运动与相互作用等物理观念的理解.
