混沌理论与BPNN耦合的径流中长期预测模型

2021-08-25王树威李建林崔延华高培强赵帅鹏

水资源与水工程学报 2021年3期

王树威，李建林,2，崔延华，高培强，赵帅鹏

(1.河南理工大学资源环境学院，河南焦作 454000； 2.煤炭安全生产与清洁高效利用省部共建协同创新中心，河南焦作 454000； 3.广西大藤峡水利枢纽开发有限责任公司，广西南宁 530000)

1 研究背景

水资源短缺是长期限制干旱、半干旱区生产生活和区域经济发展的首要因素[1]。科学、有效的中长期径流预测，有助于该地区水资源的合理规划及各种社会效益的可循环发展，并为解决旱涝灾害[2]、水利建设[3]、水能源调度[4]等问题提供有效帮助。中长期径流预报始终是水文学研究中存在的重点、难点问题[5]。目前，径流中长期预测主要分为过程驱动和数据驱动两大类[6]。过程驱动模型主要以分布式水文模型预测为主，如王杰[7]、赵奕等[8]利用SWAT和DHSVM模型对黑河上游流域的水文过程进行模拟。数据驱动主要是利用数学统计和人工智能方法进行径流的模拟和预测，如运用灰色模型(GM)[9]、支持向量机(SVM)[10]、R/S分析[11]和人工神经网络(ANN)[12]等。与过程驱动模型相比，数据驱动模型所需要的观测数据较少，可以快速建模并易于实现；而且，数据驱动模型可以通过从长期径流量时间序列中提取的非线性水流特征，产生比物理过程驱动模型更令人满意的预测效果[13]。因此，目前数据驱动的方法在径流量预测的应用中更为广泛。

江河径流是受多种因素影响的复杂系统，仅依赖单一的方法进行径流预测往往难以达到所期望的效果[14]。因而，选择合理的方法使其优点结合增补，是建立有效预测模型的关键。混沌理论(chaos theory)中的相空间重构技术可以让时间序列中隐藏的丰富的动力学分量信息得以恢复[15]，是研究复杂系统的有效工具。但目前，基于混沌理论预测的全域法、局域法等[16]研究仅能实现对径流量的短期预测，对水文预报的利用意义不大。人工神经网络(ANN)可以模拟人脑神经元处理复杂未知信息的方式，具有极强的非线性映射能力，并在水文时间序列的中长期模拟与预测上具有独特的优势[17]；BP神经网络(BPNN)是一种应用较为广泛的神经网络，它具有训练误差反向传播和预测结果准确性高的优点[18-19]。但利用BPNN进行径流量预测时，输入层神经元的个数及其取值(即径流影响因素的选择及其取值)是决定模型精度的关键。而影响径流的因素往往交织在一起，所以有些影响因素难以收集、量化；或在众多影响因素中难以确定起关键作用的因素，这导致BPNN在预测时具有较大的主观性和局限性。通过混沌相空间重构，可以量化蕴藏在径流时间序列中的影响径流各因素的个数及其取值，所以将混沌理论与BPNN结合，可使其优势互补，实现结果更优的中长期预测模型。

黑河是位于中国西北干旱地区的内陆河，其上游的径流量将直接影响整个流域地区的社会经济可持续性发展与水生态环境保护[20]。所以，莺落峡径流中长期的科学预报对提高黑河出山干流水量调度的精确度、增强水量调用工作的实时动态性管理具有重要的现实意义[21]。鉴于此，建立黑河出山径流中长期预测的混沌-BPNN等维递补模型；同时也为径流中长期预测提供新的思路和方法。

2 数据来源与研究方法

2.1 研究区概况

莺落峡水文站是黑河上游干流出山径流的控制站，设站观测始于1944年，其总径流量达15.523 9×108m3/a，多年平均径流量为49.225 9 m3/s，主要补给源为大气降水、冰川融水[22]。

2.2 数据来源

选取1944年1月-2017年12月莺落峡站888个月的实测月径流量数据资料(图1)进行建模和模型验证。径流数据来源于《甘肃河西地区内陆河水文年鉴》(第10卷第5册)[23]。

图1 1944-1917年黑河上游莺落峡水文站月径流量

2.3 研究方法

2.3.1 相空间重构

(1)延迟时间τ。用于计算参数τ的方法有很多，如自相关函数法、C-C法等。而在处理非线性时间序列方面，互信息法[24]具有更明显的优势。对于径流时间序列x(t)={x1,x2,…,xn}，假设x(t)在序列中出现的概率为P(x(t))，x(t+τ)在该序列中出现的概率为P(x(t+τ))。两者共同出现的概率为P(x(t),x(t+τ))，则互信息函数为：

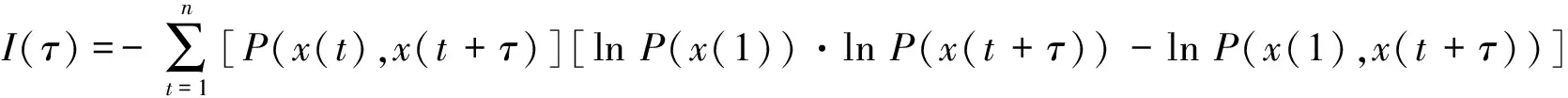
(1)

通过计算，当互信息函数曲线首次达到局部极小值时所对应的τ，即为最佳延迟时间τ。

(2)嵌入维数m。G-P关联维法、FNN法和Cao方法是确定嵌入维数的常用方法。而Cao方法[25]具有主观参数少(仅有1个主观参数τ)、信号区分能力强、计算效率高的优点。Cao方法由公式(2)计算相空间中的点在不同嵌入维数下的最邻近点的距离变化α(i,m)；再经公式(3)计算α(i,m)的均值E(m)，并通过公式(4)计算E1(m)的变化情况。最后，绘制出E1(m)-m曲线。当E1(m)的变化逐渐达到稳定时，则稳定处的m即为所求。

(2)

式中：α(i,m)为不同嵌入维数下的最邻近点的距离； ‖ ‖∞(m+1)为m+1维空间∞-范数；Yn为距离Yη最近的向量。

(3)

(4)

式中：E(m)为α(i,m)的均值；E1(m)为E(m)的变化情况；τ为延迟时间，根据时间序列的时间间隔而定，本文中τ的单位为月。

(3)相空间重构。在参数τ和m确定后，进行径流量时间序列x(t)={x1,x2,…,xn}的相空间重构[26]，得到m维的向量序列：

Yi={xi,xi+τ,…,xi+(m-1)τ}

(5)

式中：i=1,2,…,M，M=n-(m-1)τ。

2.3.2 最大Lyapunov指数最大Lyapunov指数λmax是系统是否具有混沌特征的辨识参数(若λmax>0，则系统具有混沌特征)，同时也可以确定重构序列的递补预测周期T(T=1/λmax)[27]。计算λmax的方法主要有小数据量法、Wolf法、Jacobian法、p-范数法等，其中Wolf法[28]运算简单、应用更为广泛。本文采用Wolf法计算λmax。

2.3.3 BP神经网络(back propagation neural network, BPNN) BPNN是由单个输入层、单个或多个隐含层和一个输出层组成的误差反向传播的前馈型神经网络[18-19]，网络模型中的每一层神经元都具有单向连接、双向传输交换信息的特征。通过BPNN的输出层可将输出值沿误差减小的方向，按梯度下降法逐层反向修正权值与阈值；并经多次训练迭代的向前传递与反向更新后形成达到期望的网络，最后代入测试数据进行预测验证。

2.3.4 混沌-BPNN模型将混沌理论和BPNN结合，建立径流量的混沌-BPNN预测模型，具体步骤如下：

(1)相空间重构。计算径流量时间序列x(t)={x1,x2,…,xn}的延迟时间τ、嵌入维数m和最大Lyapunov指数λmax，并在此基础上进行相空间重构。

(2)确定BPNN输入层、隐含层。嵌入维数m可以被认为是径流量影响因素的个数，将其作为混沌-BPNN模型的输入层神经元的个数；而输入神经元的取值由公式(5)确定。隐含层的节点数n可由经验公式和试凑法求得[29-30]。

(3)构建混沌-BPNN模型。将重构好的向量序列分成训练数据和验证数据。基于MATLAB神经网络工具箱，将训练好的各层网络神经元相结合，构建混沌-BPNN模型，输出预测结果。混沌-BPNN预测模型结构见图2。

图2 混沌-BPNN预测模型结构

2.3.5 模型性能评价为更好地评价预测模型的可靠性和准确性，本文选取水文预报中较为常用的4种评价指标——平均绝对百分比误差MAPE、预测精度PP、相对误差RE、合格率QR进行模型性能的评价[31]。评价指标的具体计算公式如下：

(6)

PP=(1-MAPE)×100%

(7)

(8)

(9)

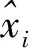
根据《水文情报预报规范(GB/T 22482—2008)》中的规定，中长期径流预报的相对误差数值百分比小于20%时为合格[32]。

3 结果与分析

3.1 黑河出山径流时间序列的相空间重构

以莺落峡1944-2017年径流量数据进行时间序列的相空间重构，由此确定径流量影响因素的个数及其取值。利用互信息法求得黑河出山径流量时间序列的延迟时间τ=5月；利用Cao方法求得其嵌入维数m=7，时间延迟τ与嵌入维数m的确定如图3所示。

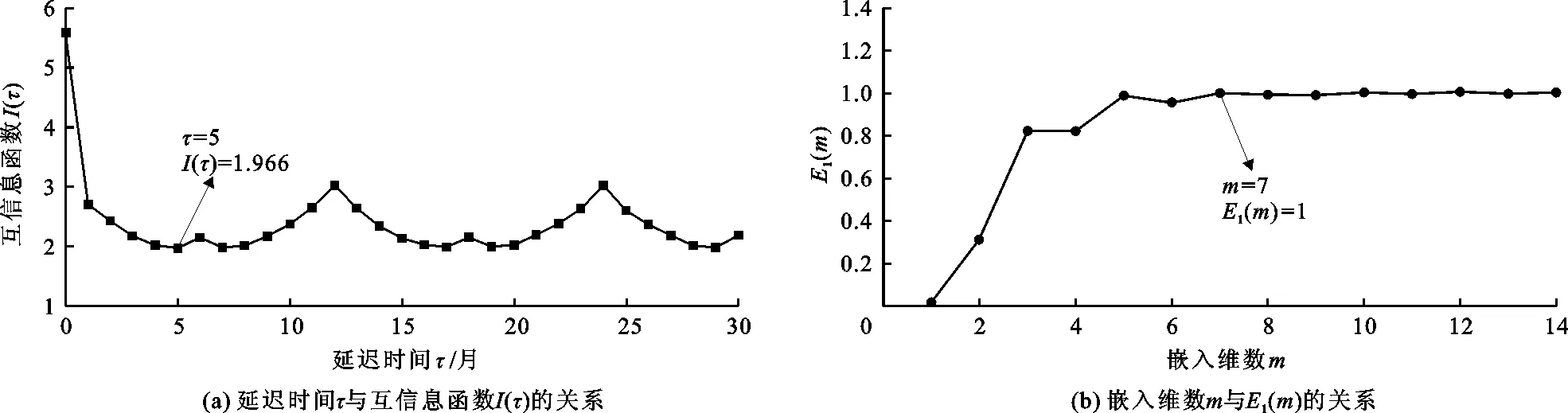
图3 时间延迟τ与嵌入维数m的确定

对黑河出山径流量时间序列进行相空间重构，得到一个延迟时间为5个月的7维向量空间Y：

(10)

3.2 月径流量的混沌-BPNN建模与验证

图4 黑河出山径流混沌-BPNN预测模型结构

为评价所建立混沌理论与BPNN耦合模型的有效性，建立黑河出山径流的BPNN模型。单一的BPNN模型是将黑河上游1944年1月至2012年12月(828个月)的径流量数据作为输入层变量进行建模训练。该模型只考虑单一时间序列，不进行相空间重构，因此BPNN的输入层神经元个数为1(即影响因素为1)。由经验公式法和试凑法求得隐含层节点数为5。经过BPNN训练后的模型可对2013年1月至2017年12月的径流量进行预测验证。

绘制径流量实测值与两种模型验证值的散点图进行对比(图5)；利用公式(7)式计算得到径流量的预测精度分别为83.57%、88.29%。结果表明，混沌-BPNN模型对黑河出山径流的中长期预测精度优于单一的BPNN模型。

图5 2013-01-2017-12两种模型的预测结果与实测值的对比

4 讨论

4.1 混沌-BPNN模型存在的主要问题

虽然混沌-BPNN模型具有较高的预测精度，但还存在2个主要问题：(1)由于径流存在周期性，对未来径流量影响较大的应该是一个周期内的数据。而混沌-BPNN模型在进行BPNN训练时，将(Y1,Y2,…,Y798)T全部作为的输入层(图4)，模型可能会因序列跨度太长(1944-2012年)，受个别极端值影响导致预测精度降低；(2)对2013年1月-2017年12月的黑河出山径流量进行模型验证，即公式(10)中x829～x888设定为未知(图6中灰色部分)；而混沌-BPNN模型将(Y799,Y800,…,Y858)T全部设为未知(图4)，则已知信息(图6中的白色部分)没有被充分利用。

图6 混沌-BPNN模型验证环节的已知信息和未知信息

4.2 混沌-BPNN模型的改进

基于以上两点，对混沌-BPNN模型进行改进。

(1)由最大Lyapunov指数可求得T=1/λmax=6.49≈6，即混沌-BPNN模型的预测周期时长为6个月。因此，可选取2012年8月-2012年12月(共5个月)径流量数据建模，即在公式中选择向量Y794～Y798，5个向量进行BPNN建模与训练。

(2)预测x829。输入Y794～Y798进行样本训练，输出层输出：

(11)

(12)

(13)

(4)重复以上步骤，每次预测去掉第一个向量，补充新的向量，保持输入层为5个向量进行BPNN训练，可得x831,x832,…,x888的预测值。由改进模型的特点，可称之为径流中长期预测的混沌-BPNN等维递补模型。

4.3 不同预测模型的性能评价

依照水文预报的规范，本文选取相对误差在20%以内的预测为合格。通过公式(8)对黑河上游60个月逐月预测的相对误差对比分析(图7)，混沌-BPNN等维递补模型明显优于另外两种模型，其各月径流量的预报误差率基本小于20%。

图7 3种模型的逐月相对误差对比(2013-01-2017-12)

根据公式(6)、(7)、(9)的计算结果(表1)，混沌-BPNN等维递补模型的平均绝对百分比误差为8.16%，低于另外两种预测模型；预测精度为91.84%，高于BPNN和混沌-BPNN，达到了90%以上，实现了较高精度的中长期径流预测。此外，通过逐月比较各模型预测值与实测值的相对误差，可以看出混沌-BPNN等维递补模型的合格率更高，为88.33%。

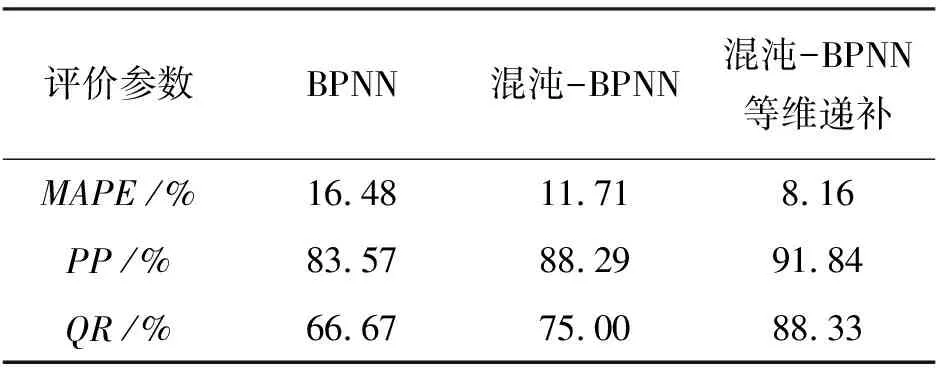
表1 3种预测模型的综合性能评价

(1)混沌理论与BPNN结合，弥补了两种方法各自的缺点，所以混沌-BPNN和混沌-BPNN等维递补模型的预测精度明显高于单一BPNN模型的预测精度。混沌理论和BPNN耦合为解决复杂非线性系统的问题，提供了强有力的工具。

(2)在利用BPNN对相空间重构后的径流量时间序列进行训练建模时，若选用全部的历史重构序列建立预测模型，则可能会因径流时间序列跨度较长而受到某些随机跳跃性数据的扰动，导致模型精度降低；若所选列太短，则可能缺少相应的建模信息，也是对历史观测数据的浪费。利用最大Lyapunov指数确定预测周期时长后，在一个周期内进行径流量预测，不仅降低了时间序列跨度的波动性、减少了对历史水文观测资料的浪费，还可避免人为随意截选样本序列进行建模的主观性。所以，混沌-BPNN等维递补模型的预测精度又明显高于混沌-BPNN的预测精度。