基于电气系统聚类的汽车线束连接正确性快速仿真分析方法

刘冰清，王 强，甘 霖，龙昭灯，何 归

（重庆长安汽车股份有限公司，重庆401120）

1 引言

汽车线束作为汽车的“神经网络”，正确的连接设计一直是整车研发的重要环节之一。传统的汽车线束设计是通过人工计算与校核，直接在2D图纸上绘制出线束产品的尺寸、接插件型号、包裹物类型、回路导通等信息，其电气原理连接信息由线束设计工程师人为进行管控［1］，图纸正确性、规范性、完整性受工程师设计经验影响较大。在快速变化的市场需求环境下，传统线束设计方法的连接正确性难以得到保证。

目前，诸多主机厂均已开始使用自动化线束设计软件进行整车线束开发，通过计算机软件模拟汽车电器件的工作状态，在未生产实物之前发现并解决问题。其中CHS（Capital Harness System）拥有较为先进的设计方法和个性化的设计流程，在国内外多家主机厂都已开始应用［2］。CHS软件内置电气原理分析功能，在完成电气原理图绘制后直接对其进行连接正确性分析，再利用该原理图直接生成线束2D图纸，保证了线束设计的全过程控制，有效提高线束设计的连接正确性。运用CHS连接正确性分析是通过对电器零部件进行建模，并利用整车电器功能检查清单建模功能检查模型，最后计算机运算检查电器功能是否正常实现，从而验证线束设计的连接正确性。由于现在汽车智能化程度提升，汽车电气连接关系也日益复杂，电器部件功能数量增加会导致仿真运算次数呈指数增长，大大地延缓了仿真分析运算速度，难以适应快速开发设计的需求，更甚者已超出了常规计算机的运算能力。

针对上述问题，本文提出了一种快速线束连接正确性分析方法，通过功能配置对整车电气系统进行划分，再对各电器系统进行失效模式相关性聚类，最后再对各类电气系统进行功能仿真分析，有效降低仿真运算次数的同时保持连接正确性检查的准确度，且其计算量能被常规计算机所接受，适用于复杂电气连接关系的汽车线束连接正确性分析。

2 基于CHS汽车电气原理仿真分析

CHS电气原理仿真通过对电器零部件进行建模，并利用整车电器功能检查清单确定功能检查模型，最后计算机运算检查电器功能是否正常实现。针对不同的仿真需求，CHS提供了定性分析与定量分析两种运行方式，定性分析状态下不进行任何数字计算，定量分析需要引入零件的各种参数，并赋予端节点之间连接线不同的电阻值等用于计算整个电路的多种数据。由于连接正确性仅需要判断节点之间是否正确接通，为实现计算机快速完成仿真运算，通常选用定性分析。

2.1 电器零部件建模

CHS的电器零部件建模需要完成模型接口参数设定、模型电器结构设定、模型电器行为设定。模型接口参数包含该电器零部件可能发生变化的参数以及仿真时需要监控的参数。电器结构用于表示用电器各引脚在内部的逻辑连接关系，具有电相关的引脚需用线进行连接。电器行为采用状态机进行编程。定性分析状态下不进行任何数字计算，需进行导通演示的电阻用ZERO（零）、MEDIUM（负载）、INFINITE（无穷）表示回路状态。电器零部件建模如图1所示。

图1 电器零部件建模

2.2 电器功能建模

功能模型利用整车电器功能检查清单建立，模型中各特征分组表示该电器系统需要实现的功能，子特征表示系统子零部件需要实现的功能。子特征集内可以创建响应函数，用于标识电器执行该功能的响应，单一子特征集可由多个响应函数组成。例如：子特征集“前照灯点亮”需由“左前照灯点亮”响应函数与“右前照灯点亮”响应函数组成。响应函数下可创建控制函数，控制函数用于表示电器执行该响应所需的外界环境的输入，同理响应函数下可创建多个控制函数，控制函数之间由“和”、“或”、“非”3个符合进行控制逻辑的组合。响应函数需要定义其失效与自发。整车功能模型设定如图2所示。

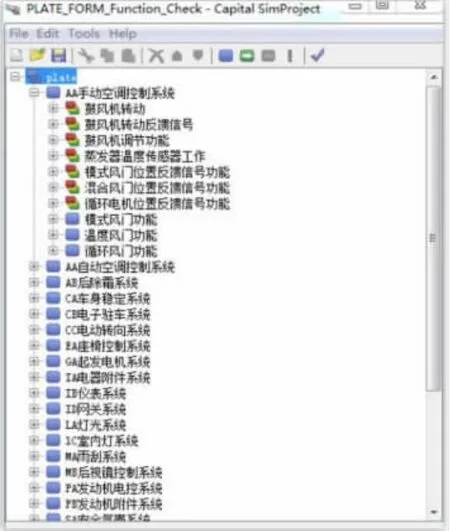
图2 整车功能模型设定

2.3 连接正确性仿真分析

完成电器零部件建模与功能模型建模后，可通过软件进行检查功能模型中各功能是否正确实现，如果系统发现可能存在的功能问题，则会显示这些问题，以及问题发生时候的开关控制组合，从而完成线束连接正确性检查。功能问题报告如图3所示。

图3 功能问题报告

3 电气分系统聚类

在汽车电气连接关系日益复杂的背景下，整车电器设计为了应对市场的快速变化，电气原理设计通常会根据产品策划输出的电器功能配置表将整车电气原理划分为多个电气分系统。由于这样划分的电气分系统并不是完全独立的，各系统之间仍存在大量信号传输；如果直接在这些系统中进行连接正确性仿真分析，虽然可以极大地压缩仿真分析时间，但是大量的系统间连接关系将无法仿真分析到，从而造成问题漏检。

为了平衡仿真时间与正确性，本文提出了一种汽车电气系统聚类的线束连接正确性快速分析方法，首先判断失效模式库中各情况与电气分系统的相关系数：

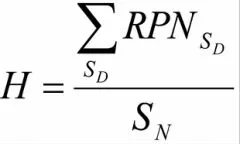
式中：SD——失效模式库中与该系统相关的因子数量；SN——失效情况所涉及因子总数；RPN=严重度（S）×频度（O）×探测度（D）——失效模式库中对失效的风险评估数；然后将已得到的电器分系统与失效情况相关系数按照失效情况的顺序排列为数组an=［H］。计算各数组内均值，选取数组an均值最大对应的电器分系统作为第一个聚类中心进行聚类［3］。

本文采用K均值的方式对系统进行聚类，首先按照如下公式计算各数组到聚类中心的欧式距离：

并计算所有样本之间距离的平均距离：

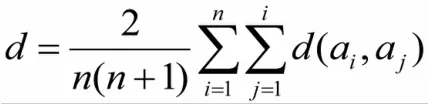
把与已有聚类中心距离大于平均距离d的样本方差置空，在剩余样本中选取均值最大的那个样本作为下一个聚类中心；重复该步骤，得到k个聚类中心；在本文实验设k=5。然后计算每个数组到各个初始聚类中心的距离，按欧式距离最近原则将每个数组对应的电气系统分到各个类；然后按照平均法更新各个类的质心，作为新的聚类中心，计算每个数据对象到新聚类中心的距离d，按最近距离原则将每个数组对应的电器系统原理图分到各个类；计算准则函数E：

判断E是否收敛，若收敛，则结束，输出最终聚类结果；若不收敛，则再次更新聚类中心并重复聚类步骤。

4 基于电气分系统聚类的连接正确性分析

本文方法流程如图4所示。通过电气分系统聚类，原电器分系统根据失效模式相关性聚为多个类，对于每个类可单独进行电气原理仿真分析，当每个类都进行仿真分析后，可认为整车电气原理通过了仿真分析，可进行下一步的试生产与实物验证。本文以某量产项目的CHS电气原理图为例用以验证本文仿真方法的有效性，该项目原理图已完成过整车级电气功能分析，通过人为设定100个设计问题进行验证，本文通过检查运算次数，设计问题检出率和设计问题误检率对最终检查模型进行评估。设计问题检出率表示被检出问题占总设定问题的比例，误检率表示系统错误判断的设计问题占总检出问题的比例，详见表1。

表1 中O表示仿真分组范围内开关数量。从表1结果可以得出，本方法较全局仿真算法误检率下降了13%，检测率仅降低了1%，同时，相对于系统仿真算法误检率上升了2%，检测率提高了29%，由于误检出来的问题可以通过设计人员判断再次排除，而漏检项往往会产生设计错误，就准确率来说全局仿真算法最优，其次为本文算法，最差为分系统仿真。同时将本文方法与平均分组算法进行对比，平均分组是将系统按照排列顺序直接分为一组在组内进行仿真分析，结果可以看出，两种方法运算次数相近，但是本文方法准确率较平均分组方法提升了20%，证明本文系统聚类方法的有效性。

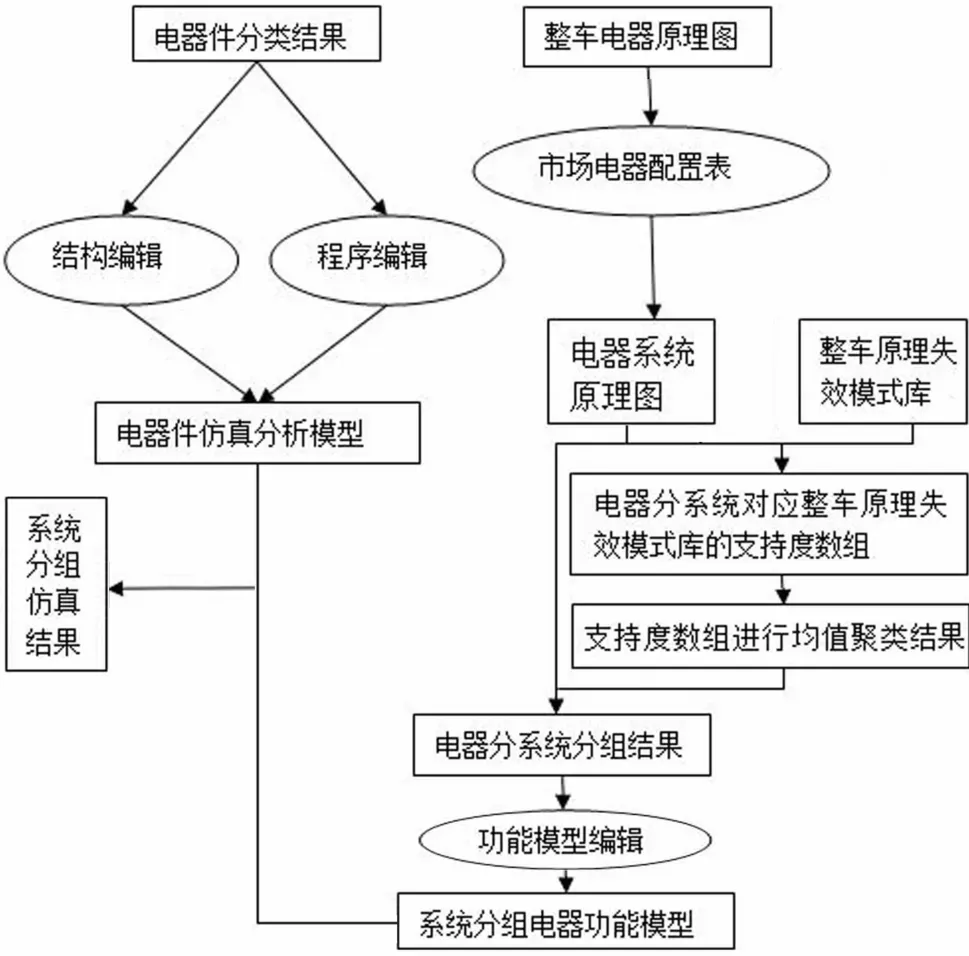
图4 本文方法流程图

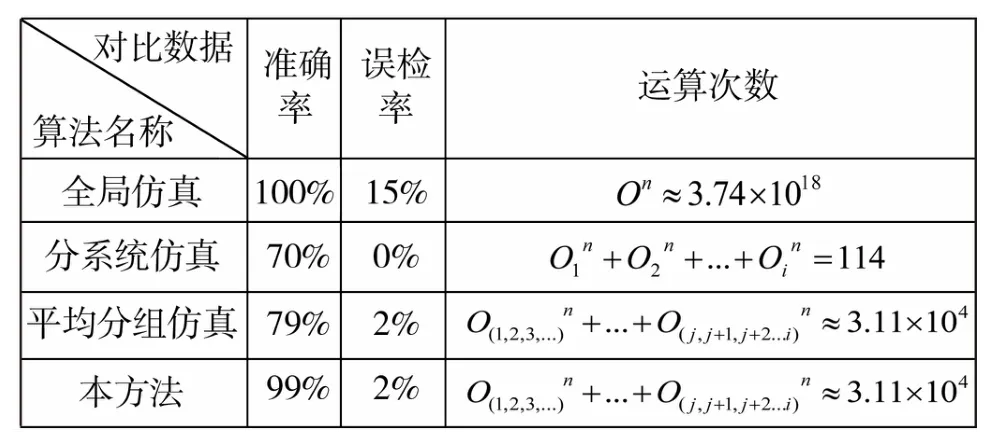
表1 本方法与全局检查以及系统检查算法的准确率以及时间对比

结合运算次数对四者进行了对比，从结果看出本算法较全局仿真大大降低了运算时间，同时检测率未明显下降。

表2 为本算法分类数量K不同时算法的检查率与算法时间对比，通过表格数据可以看出，随着分类数量的增加，检测率逐渐下降，算法运算时间也同时下降，运算时间下降趋势呈指数形式，在分类数量达到一定程度后继续增加分类数量时间收益并不高，且检测率下降严重，本方法旨在解决普通计算机无法满足的大运算量问题，因而在普通计算机能满足运算的条件下应尽量减少分类数量。

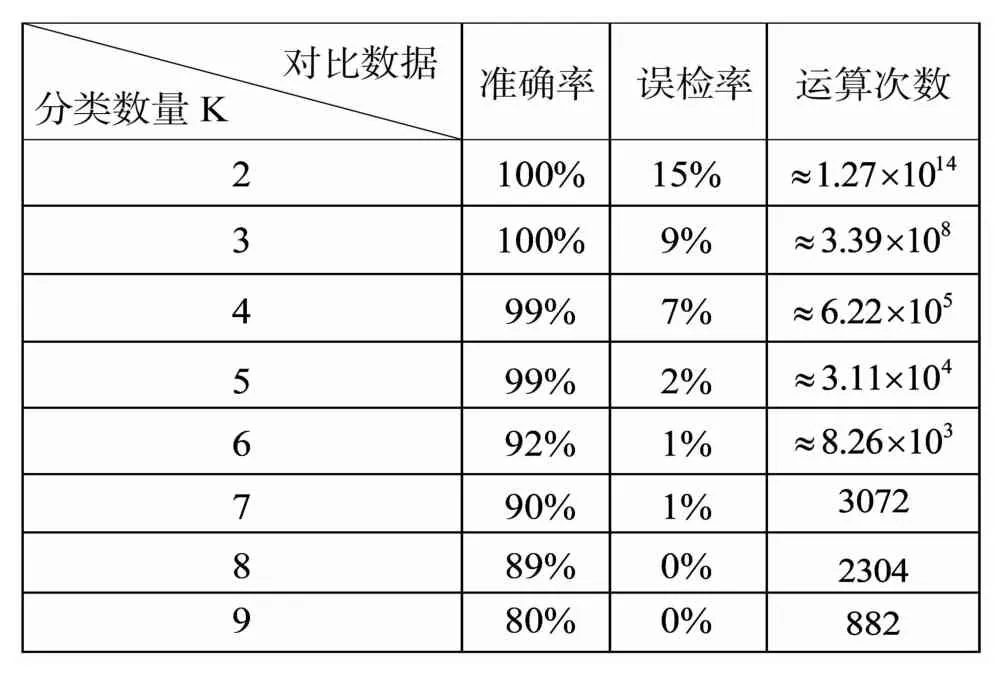
表2 本发明聚类数量结果对比

5 结论

综上所述，本文方法根据市场需求的功能配置对整车电器原理进行划分，在需求发生变化时，能够针对配置变化涉及的系统进行更新，相对于整车全局仿真，该仿真模型具有更好的适应性，仿真速度也得到了有效提高。同时仿真模型将失效风险评估数引入各个电器分系统相关系数中，有效地利用问题的关重信息，在提升运算速度的同时有效避免了关键信息丢失。系统分组数量以及分组方式仍对连接正确性仿真分析结果有较大的影响，后续仍需对分组数量以及分组方式进行更加深入的研究。