一种基于三支聚类的快速KNN算法

赵书宝，姜春茂

(哈尔滨师范大学 计算机科学与信息工程学院，哈尔滨 150025)

1 引 言

分类是数据挖掘领域中非常实用的技术，常见的分类算法有决策树、神经网络、KNN和支撑向量机等.其中KNN算法以其理论成熟、思想简单和准确率高的特点得到了广泛的应用.KNN算法的基本思想是先从给定的训练样本中找到与待测样本距离最近的K个点，然后计算K个点中属于每一类的条件概率，最后通过投票得出分类结果.传统的KNN算法进行分类时对每一个待测样本都需要搜寻整个训练集，计算与所有训练样本的距离，然后选出距离最近的K个点.KNN算法的分类效率与训练样本的规模呈正比，训练样本的规模越大，则分类效率越低.因此，一系列快速KNN算法被提出，以解决KNN算法在面对大规模数据分类效率较低的缺陷.

针对传统KNN算法分类效率较低的情况，许多学者提出了改进的KNN算法.分析发现所提出的算法大致分为两种类型，第1种是对训练样本裁切，减少训练样本的规模[1-5].第2种是通过快速搜索算法，快速寻找距离最近的K个近邻样本[6].如文献[1]针对文本分类时，样本规模较大导致分类效率降低的现象，引入了粗糙集的近似集模型，将所有的样本划分到类别的上近似集合和下近似集合，从而根据待测样本与类别的位置关系，选择合适的类别，从而提高算法的分类效率.文献[2]通过基于界标的谱聚类算法将训练样本划分为多个类簇，分别计算待测样本与所有类簇中心的距离，使用距离最近的类簇中的对象重新构造训练集进行KNN分类，有效降低训练集的规模.文献[3]针对传统的KNN算法近邻点个数固定的问题，提出了一种使用环形过滤器的自适应K值的KNN算法，算法通过计算样本之间的相似度动态选取K值，相比于传统的KNN算法，不仅提高了分类的效率，而且提高了分类的准确率.文献[4]针对KNN算法在面对大规模数据时分类效率降低的问题，提出了一种基于CUDA的并行化KNN算法，实验表明算法在保证分类准确率的基础上，提高了分类的效率.文献[5]首先将训练样本中相似度较高的数据聚为一个类簇，然后以测试点为中心构建环形过滤器，对待测样本进行分类，有效减少了训练样本的规模.

在对训练样本进行裁切时，最常用的方式是聚类.基于聚类的快速KNN算法[2，3，5，7]通过在训练样本上进行聚类，将样本划分为多个类簇，然后选取某一类簇中的对象作为训练集，但传统的聚类算法大多是一种二支聚类的结果.类簇之间具有清晰的边界，在处理对象与类簇之间缺乏明确的归属关系的数据时无法清晰的描述类簇边界模糊的特征.当待测样本位于类簇的边界时，容易带来近邻点的缺失，从而引起分类准确率的降低，因此基于聚类的快速KNN算法，大多以降低分类准确率为代价，提高分类的效率[2].

三支聚类[8-13]在二支聚类的基础上引入了中间域的概念，将对象与类簇之间的关系分为3种，即对象确定属于该类簇，对象确定不属于该类簇和不确定对象是否属于该类簇.三支聚类能够更好的描述类簇边界模糊的结构特征，避免了二支聚类的缺陷.因此，本文针对传统聚类改进的KNN算法中存在的问题，提出了一种基于三支聚类的快速KNN算法(TWC-KNN).其基本思想是首先通过三支聚类将训练样本划分为多个类簇，每个类簇均由核心域和边界域两个部分组成.然后通过分析待测样本与类簇之间的位置关系，如果待测样本位于类簇的核心域，则使用核心域中的对象作为训练样本进行KNN分类，如果待测样本位于多个类簇的边界域，则使用这些边界域的对象作为训练样本进行KNN分类，如果待测样本不属于任何类簇的核心域和边界域，则使用所有的训练样本进行KNN分类.

本文组织如下：第2节分析了原有的改进型KNN算法的缺陷以及TWC-KNN算法的优势.第3节回顾了阴影集和三支聚类的基本概念.第4节提出了一种基于阴影集的三支聚类算法，并通过该算法对训练样本进行聚类，去除明显不属于待测样本K近邻的对象，从而提高KNN算法的分类效率.第5节在UCI数据集上进行试验，通过与传统KNN算法和3种改进的KNN算法的对比验证了本文中所提出算法的优势.第6节总结全文，并分析了未来的研究工作.

2 问题描述

基于聚类改进的KNN算法大多采用首先在训练样本上聚类，然后找到与待测样本距离最近的类簇中心，使用该类簇所包含的对象构建训练集进行KNN分类.这样可以有效减少训练样本的规模，提高KNN算法的分类效率.然而目前采用的聚类算法大多是一种二支聚类的结果，即对象确定属于该类簇或确定不属于该类簇，类簇之间具有清晰的边界.这种聚类结果在某些数据集上无法很好的表述类簇边界模糊的特征，当待测样本位于类簇边界时，仅根据距离选取最近的类簇，并使用该类簇中的对象构建训练集进行KNN分类，容易引起误分类，降低KNN分类的准确率.为了更好的描述文本所阐述的思想，通过如下两个示例来描述二支聚类改进的KNN算法分类时产生的问题，以及三支聚类改进的KNN算法的优势.

二支聚类算法对样本进聚类的结果如图1所示.通过二支聚类将训练样本划分到C1和C2两个类簇，二支聚类的结果中对象只能属于一个类簇.当待测样本位于x1和x2时，二支聚类算法将其划分到不同的类簇，此时对x1和x2进行KNN分类时容易带来近邻点的缺失.而在传统的KNN分类中两者可能属于同一类别.产生这一问题的主要原因是传统的二支聚类算法无法很好的描述类簇边界模糊的特征.因此容易产生较高的误分类代价，降低KNN算法的分类准确率.

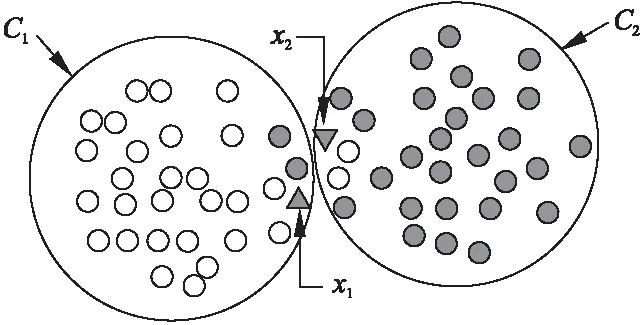
图1 二支聚类的结果

三支聚类算法对样本进行聚类的结果如图2所示.通过三支聚类将训练样本划分到C1和C2两个类簇，三支聚类中的每一个类簇由两个子集表示，即Ci=(Co(Ci)，Fr(Ci)).位于核心域Co(Ci)的对象表示确定属于类簇Ci，位于边界域Fr(Ci)的对象表示可能属于类簇Ci.当待测样本位于x1和x2时，三支聚类算法将其划分到类簇C1和C2的边界域.因此在进行KNN分类时使用类簇C1和C2边界域中的对象构造训练集进行KNN分类.这样可以有效克服二支聚类改进的KNN算法在面对类簇边界模糊的数据时准确率较低的缺陷.基于三支聚类的改进KNN算法在保持较高分类准确率的同时，能够有效降低训练集的规模，提高分类效率.

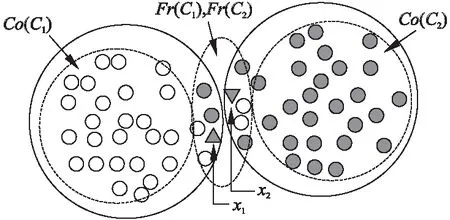
图2 三支聚类的结果

3 基本概念

3.1 阴影集

阴影集[14，15]由Witold Pedrycz于1998年首次提出.阴影集由模糊集演化而来，增强了结果的可解释性并将传统的模糊集转化为三支逻辑.下面给出阴影集的定义.

定义1.[14]在论域U中，给定阴影集S，一对阈值(α，β)，并且有0<β<α<1.将论域U中所有的对象根据隶属度μA(x)映射到集合{0，[0，1]，1}中.即：

(1)

其中隶属度μA(x)表示对象x隶属于概念A的程度.如果隶属度函数μA(x)大于或等于阈值α，则通过提升操作将对象x的隶属度μA(x)提升到1.如果对象x的隶属度μA(x)小于或者等于阈值β，则通过降低操作将隶属度μA(x)降低到0.如果对象x的隶属度μA(x)在α和β之间，则将对象划分到阴影区域.图3表示一个阴影集，阴影集通过隶属度函数μA(x)将所有隶属度高于阈值α的对象的隶属度提升到1，将所有隶属度低于阈值β的对象的隶属度降低到0，阴影区域则包括所有隶属度在α和β的对象.

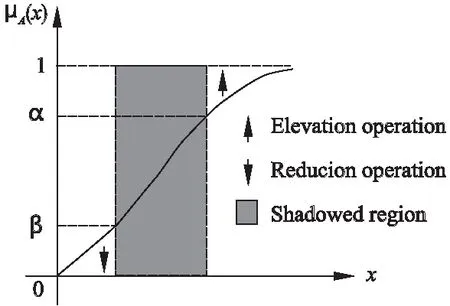
图3 阴影集

3.2 三支聚类

于洪教授[11]首次将三支决策[16-22]引入到聚类分析中，提出了三支聚类理论.王平心教授[12]借鉴数学形态学中收缩和扩张的思想，提出了一种基于数学形态学的三支聚类算法，该算法可将传统的二支聚类的结果扩展为三支聚类的结果.姜春茂教授[23]分析了云任务的多样化需求和资源动态的特性，提出了一种基于负载敏感的云任务三支聚类评分调度算法.

传统的聚类算法是一种二支聚类的结果，即对象和类簇之间的关系只有两种，对象确定属于该类簇或者对象确定不属于该类簇.给定一组数据U={x1，x2，…，xn}，三支聚类的每个类簇表示为Ci={Co(Ci)，Fr(Ci)}，即类簇Ci由两个子集构成，分别是类簇Ci的核心域Co(Ci)和边界域Fr(Ci).类簇的琐碎域表示为Tr(Ci)=U-(Co(Ci)∪Fr(Ci))，琐碎域包含的对象表示确定不属于该类簇.类簇Ci的3个域满足如下条件：

1)Co(Ci)∪Fr(Ci)∪Tr(Ci)=U

2)Co(Ci)∩Fr(Ci)=∅

3)Co(Ci)∩Tr(Ci)=∅

4)Tr(Ci)∩Fr(Ci)=∅

上述4个条件说明任何一个类簇的核心域、边界域和琐碎域之间的并集为论域U.核心域、边界域和琐碎域两两互不相交.

4 基于三支聚类的快速KNN算法

4.1 构造三支聚类

三支聚类的类簇由核心域和边界域两个集合组成，而二支聚类的类簇则是单个集合.本文尝试通过阴影集的提升与降低操作对FCM聚类的结果进行处理得到三支聚类的结果.FCM聚类算法通过最小化类内间距不断更新隶属度，在所有的对象对所有的类簇的隶属度都确定后，生成对象与类簇的隶属度关系矩阵.通过隶属度表示对象与类簇之间的关系，对于隶属度高于阈值α的对象，通过提升操作将隶属度提升到1，表示对象确定属于该类簇.对于隶属度低于阈值β的对象，通过降低操作将隶属度降低到0，表示对象确定不属于该类簇.隶属度在α和β之间的对象划分到阴影区域，表示对象可能属于该类簇.最终得到三支聚类的结果.

给定一组数据U={x1，x2，…，xn}，通过FCM将论域U中的对象划分为k个类簇C={C1，C2，…，Ck}对象x与类簇Ci之间的关系通过隶属度μCi(x)表示.给定一对阈值(α，β)并且有0<β<α<1，根据隶属度μCi(x)与阈值α和β的关系，有如下3种类型的操作：

EO={μCi(x)=1|μCi(x)≥αi}

RO={μCi(x)=[0，1]|βi<μCi(x)<αi}

SO={μCi(x)=0|μCi(x)≤βi}

(2)

通过对象的3种操作，可以得到三支聚类的核心域、边界域和琐碎域：

Co(Ci)={x∈U|μCi(x)=1}

Fr(Ci)={x∈U|μCi(x)=[0，1]}

Tr(Ci)={x∈U|μCi(x)=0}

(3)

为了计算最优阈值(α，β)，Zhang[24]将博弈论引入到阴影集，通过求解纳什均衡获得最优阈值.Pedrycz[14]将阴影集中提升和降低操作变化的隶属度之和与阴影集中对象数量之差的绝对值作为优化函数，通过求解优化函数的最小值获得最优阈值.Deng[25]将贝叶斯风险决策引入到阴影集中，寻找风险最小时的阈值.本文采用Pedrycz所提出的方法，通过求解如下优化函数获得最优阈值α和β.对于任意类簇Ci，μCi(x)表示对象x对Ci的隶属度，通过分析对象与类簇的隶属度关系，构建优化函数：

(4)

其中：

-card{x∈U|β<μCi(x)<α}|

算法的主要步骤如算法1所示：

算法1.three-way clustering based on shadowed set

1. input：a set of dataU={x1，x2，…，xn}，the number of clusters k

2.output：C={(Co(C1)，Fr(C1))，(Co(C2)，Fr(C2))，…，(Co(Ck)，Fr(Ci))}

3. obtaining membership matrix and cluster center through FCM algorithm

4. calculate the optimal thresholdαandβfor each clusterCithrough the shadowed sets

5. for each clusterCi：

6. foriin range(n)：

7. ifμCi(x)>α：

8. dividexintoCo(Ci)

9. else ifμCi(x)<β：

10. dividexintoTr(Ci)

11. else：

12. dividexintoFr(Ci)

13. returnC={(Co(C1)，Fr(C1))， (Co(C2)，Fr(C2))，…，(Co(Ck)，Fr(Ci))}.

4.2 快速KNN分类

通过三支聚类对训练样本进行裁切，从而构建新的训练集.根据待测样本y与类簇Ci的隶属度可知待测样本与类簇Ci有3种位置关系，当待测样本y与类簇Ci的隶属度高于给定的阈值α时，则使用类簇Ci核心域的对象构建训练集，然后进行KNN分类.当待测样本y位于多个类簇的边界域时，则使用这些边界域中的对象作为训练样本进行KNN分类.如果待测样本不属于所有类簇的核心域和边界域时，则使用全体训练样本进行KNN分类.

基于阴影集三支聚类的改进KNN分类算法主要步骤如算法2所示：

算法2.improved KNN classification based on three-way clustering of shadowed set

1. input：C={(Co(C1)，Fr(C1))，(Co(C2)，Fr(C2))，…，

(Co(Cn)，Fr(Cn))}，

test sampleY={y1，y2，…，yn}.

2. output：the predicted value of the label of the test sample.

3. foryiinY：

4. foriin range(n)：

5. ifμCi(y)>α：

6. construct training set using objects inCo(Ci)region.

7.elseifβ<μmi(x)<α：

8. construct training set using objects inFr(Ci)region.

9. ifyinot belong to any cluster：

10. construct training set using all training objects

11. run KNN algorithm.

5 实验数据分析

5.1 对比算法与实验数据集

为了比较本文所提出的基于三支聚类的快速KNN算法(TWC-KNN)是否具有更好的性能，本文选取了一些对比算法，包括传统的KNN算法和3种改进的快速KNN算法，RC-KNN[2]、LC-KNN[2]和FCM-KNN[26].实验选取了8组UCI真实数据集，表1给出了8个UCI数据集的详细信息包括样本数、属性数和类别数.训练数和测试数是以7∶3对实验数据集进行分割，所获得的样本个数.

5.2 算法性能分析

为验证所提出算法的性能，本文比较了所提出的算法与4个对比算法的准确率、平均计算每一个对象参与运算的样本的个数和算法的运行时间，实验共重复了50次，最终结果取平均值，分类个数为样本的真实个数，具体结果如表2-表4所示.

从表2可知，所提出的算法在Waveform、Spambase、Satimage、Avila和Parkinsons均获得了最高的分类准确率，在Letter、Pendigits和Segmentation3个数据集上分类准确率略低于传统的KNN算法，在整体上看TWC-KNN仍高于其余3种改进的KNN算法.从8种不同数据集的平均准确率来看，所提出的算法略微高于传统的KNN算法，而其他3种改进的KNN算法的准确率则低于传统的KNN算法.从表3可知，所提出的TWC-KNN有效减少了参与运算的对象的平均个数.传统的KNN算法对训练样本不做任何处理，因此参与训练的样本最多.在Spambase数据集上， 所提出的算法对训练样本裁切的比例最少，参与运算的样本为训练样本的89.16%.而在Parkinsons数据集上，所提出的算法参与运算的对象的平均个数为训练样本的1.87%， 裁剪的样本比例最多.

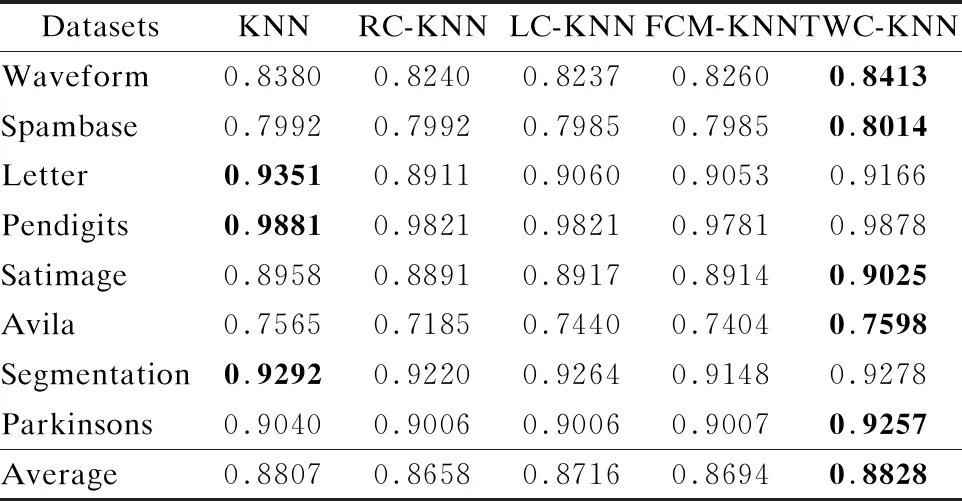
表2 5种KNN分类算法的平均准确率对比

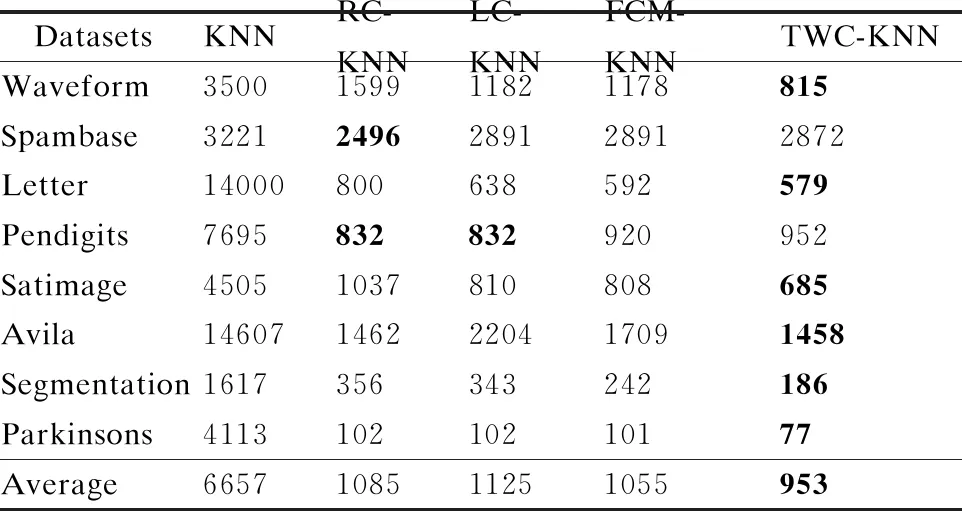
表3 不同算法参与运算的对象的平均个数

从表1可以发现Spambase数据集类别数最少为2个，Parkinsons数据集的类别数最多为42个.因此类别个数与分类的效率可能存在一定的关系，类别数越多，则分类的效率越高.表4展示了不同算法的平均运行时间，从中可知Spambase数据集上，TWC-KNN算法的运行时间高于传统的KNN算法，这主要是由于该数据集上类别数较少，因此训练样本裁切的比例较少，而在分类时需要判断并选择合适的类簇作为训练集，因此算法的消耗时间高于KNN算法，其他3种改进的KNN算法，RC-KNN、LC-KNN和FCM-KNN均出现了这种现象.在Letter数据集上，TWC-KNN算法运行时间提升的最高，这主要是Letter的训练样本个数和维数较高，因此传统的KNN算法分类时间较高，TWC-KNN算法裁切后，训练样本的规模大幅度降低，因此在分类时间上提升最高.

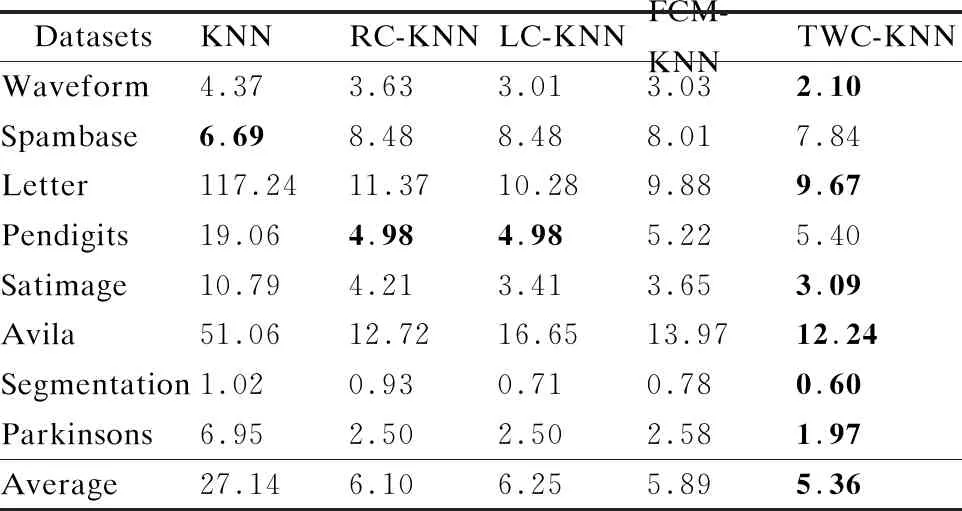
表4 不同算法的平均消耗时间(time/s)

5.3 分类簇数与算法效率的关系分析

根据5.2节可以发现，分类簇数越少，则算法的效率越低，分类簇数越多，则算法的效率越高，为验证这一结论是否具有普遍性，本文设置了以下实验，在8种不同的UCI数据集上，对比了所提出的TWC-KNN算法与传统的KNN算法和3种改进的KNN算法在不同规模的分类簇数下算法所需的时间与准确率.分类簇数设置为5，10，15，20，25，在不同的分类簇数下均进行了50次重复，最终结果取其平均值具体结果如图4和图5所示.

从图4可以看出，在不同的分类簇数下KNN算法消耗的时间基本稳定，这是由于KNN算法对训练集并未裁切，而所提出的TWC-KNN算法与3种对比的改进KNN算法随着分类簇数规模的增加，分类所消耗的之间大幅度的降低，但随着分类簇数的增加到一定程度，分类效率的增加趋向于平稳，在Segmentation数据集上由于样本的规模较小，所以所提出的算法并未展现较好的分类效率，这也反应了所提出的TWC-KNN算法更加适合于样本规模较大的数据集.从图5中可以看出，随着分类簇数的不断增加，所提出的TWC-KNN算法有轻微的下降趋势，这主要是由于所提出的算法为近似算法，随着分类簇数的不断增加，所产生的边界越多，越容易引起近邻样本的缺失，因此分类准确率有所降低.从图4和图5可知，TWC-KNN算法在各个分类簇数规模下，分类准确率都高于其它3种改进的KNN算法，且时间消耗也小于其它3种改进的KNN算法.总体来看，当数据集的分类数较多时，考虑到分类准确率的要求，一般建议以真实分类数进行聚类，划分类簇，当数据集的分类数较少时，一般建议类簇数在10-15.总体来看TWC-KNN相比于其他3种改进的KNN算法，在分类准确率和分类效率方面均有提高，因此所提出的算法是可行的.

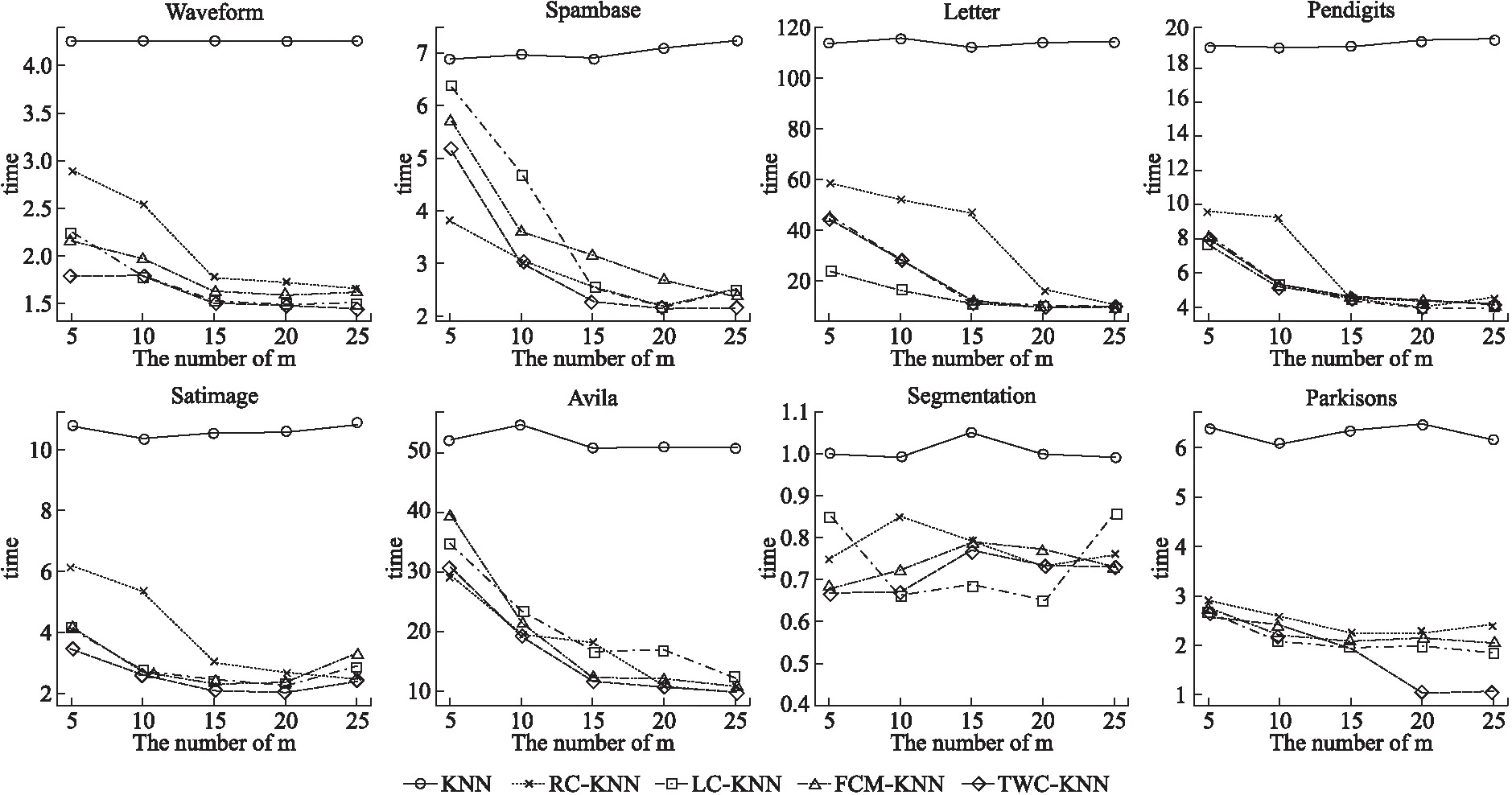
图4 不同分类簇规模下算法平均消耗时间

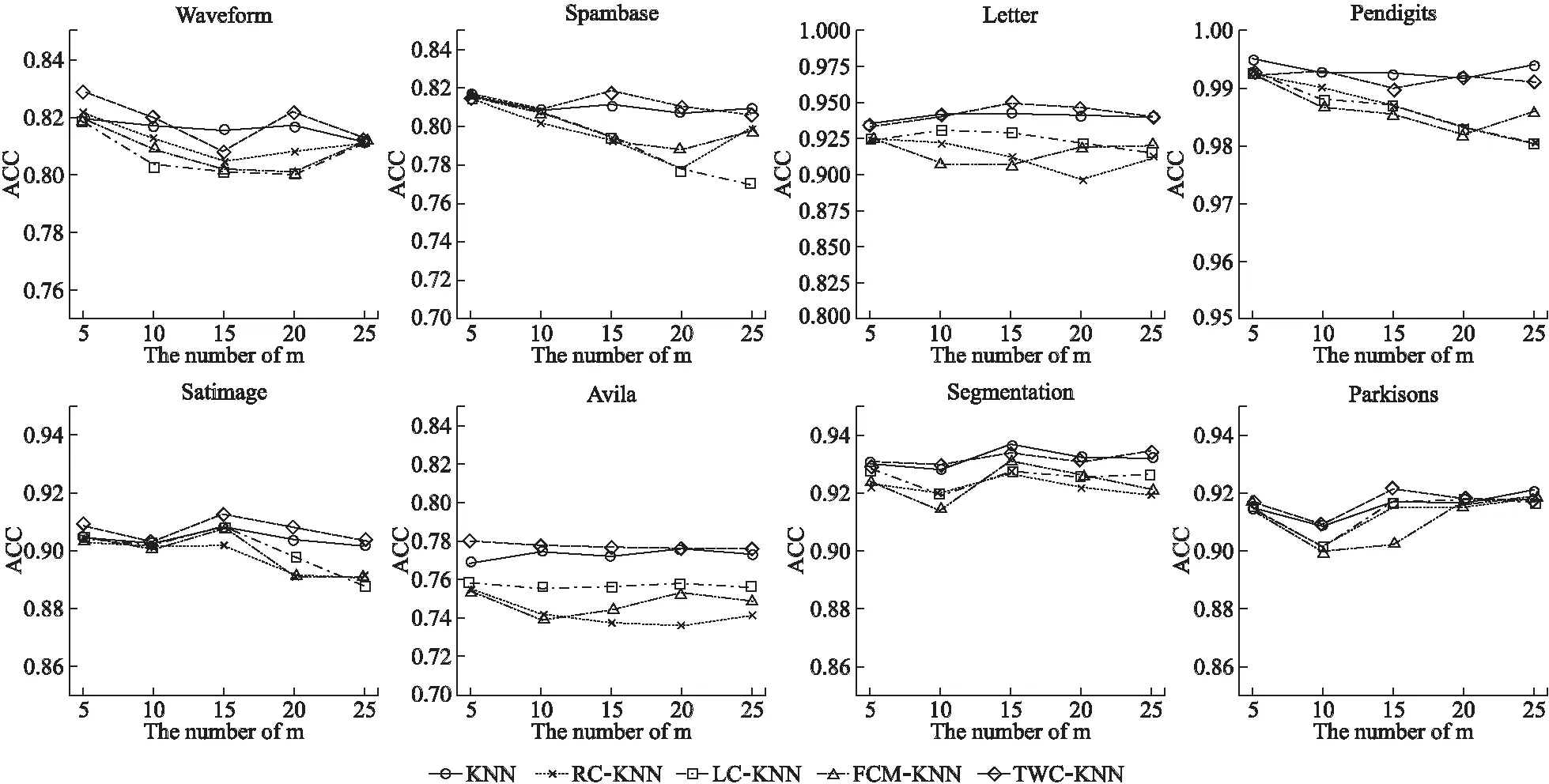
图5 不同分类簇规模下算法的平均准确率

5.4 训练样本规模与分类准确率的关系分析

通常随着训练样本规模的减少，分类的准确率会逐渐降低.为分析本文所提出的算法随着训练样本规模的减少，分类准确率是否相对于原有的KNN算法和3种改进的KNN算法呈现显著的降低，为此本文设计了如下实验，在8种不同的UCI数据集上，分别运行本文所提出的算法以及其他4种对比算法，聚类的类簇数为真实类簇数，训练样本的规模占总样本的规模的比例依次减少，分别为90%，80%，70%，60%，50%.实验结果如图6所示.

从图6可以发现，随着训练样本规模的减少，分类的准确率在8种数据集上均有一定程度上的降低，但所提出的TWC-KNN算法与传统的KNN算法和3种改进的KNN算法相比降低程度趋于相同，因此随着训练样本规模的降低，本文所提出的算法相比于对比算法并不会带来分类准确率的显著降低.

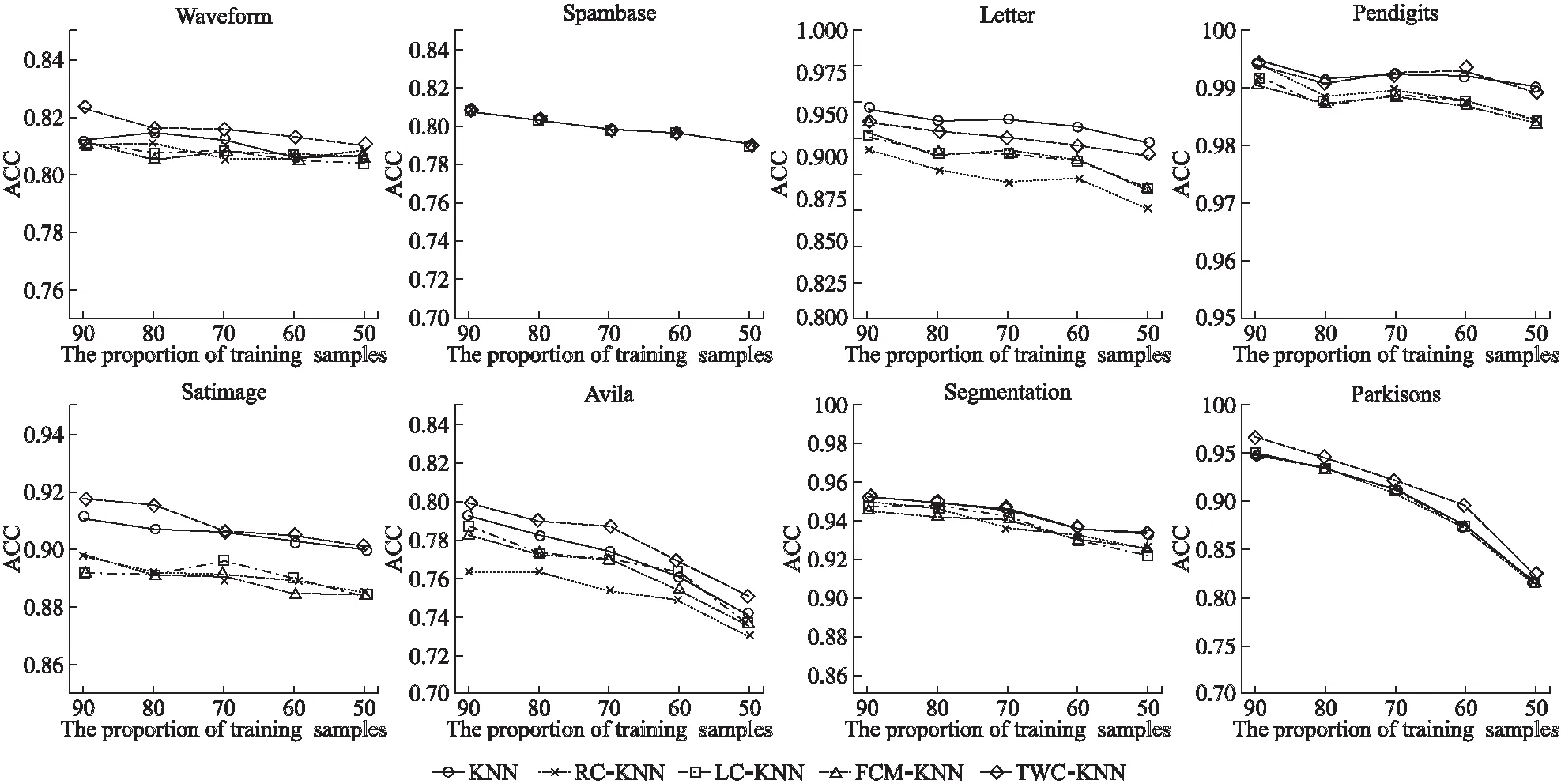
图6 不同训练样本规模下算法的平均准确率

6 总 结

本文针对现有聚类改进的KNN算法分类准确率较低的问题，提出了一种基于三支聚类的改进KNN算法.该算法首先通过阴影集对FCM聚类结果的隶属度矩阵进行处理，得到三支聚类，从而将训练样本划分为多个类簇，通过分析待测样本与类簇中心的位置关系重新构造训练集，然后进行KNN分类，有效的去除了大量确定不属于待测样本K近邻的对象，且克服了现有的改进KNN算法分类准确率下降的缺点.实验结果表明了本算法相比于传统的KNN算法和3种改进的KNN算法，在分类准确率和分类效率方面均有所提高.