换热管周围声流强化对流传热的数值模拟

杨延锋，姜根山，于 淼

(1.华北电力大学 能源动力与机械工程学院，北京 102206； 2.华北电力大学 数理学院，北京 102206)

近年来，声波(或振动)诱导振荡流强化热、质传输过程的研究已受到广泛的关注[1-3]。理论研究表明，声波作用于物体或物体发生自激振动时，不论何种形式，物体周围均可形成2种不同的流场成分[4-5]：(1) 依赖于激励频率的自由振荡流；(2) 与时间无关的具有漩涡特性的稳定声流(或定常流)。这表明，声波(或振动)诱导振荡流对热、质传输速率的影响取决于这2种不同的流场特性。声流的形成是由于声波在固体声学边界层内的热黏性损耗而产生的时均净流量，由雷诺应力驱动，由此在声学边界层内形成的声流称为内涡流；而通过动量和涡量的传递，又可在声学边界层外诱导出尺度更大但强度较弱的外涡流[6]。声流的存在可以破坏边界层结构，从而降低热、质的传输阻力。Gopinath等[7]理论分析了大流雷诺数条件下声流对传热的影响，指出声流强化传热的效果与频率成反比，而与声强成正比。对于声流结构的研究，Bahrani等[8]利用粒子图像测速法(PIV技术)可视化了振动圆柱外的声流结构，清晰呈现了内涡流和外涡流。林同骥等[9]对同心圆柱间内柱作小振幅(Re≪1)振荡诱导的稳态漩涡流进行了数值模拟，并通过实验可视化了稳态涡流的结构。然而，国内外对声流引起的热对流问题还鲜有研究。因此，笔者建立了行波场中单换热管外声流强化传热的数值计算模型，试图探究声流对传热的影响机理。

在数值和实验研究方面，Gupta等[10]数值模拟了具有幂律分布的脉动流对加热圆柱传热的影响，结果表明，在适当的速度幅值、雷诺数和幂律指数条件下，脉动流可以增强流体的整体混合和传热过程。Molochnikov等[11]实验研究了加热圆柱在脉动交叉流中的传热问题，得到圆柱体表面局部传热系数随脉动频率和幅值的分布规律，且传热效果随着频率和脉动雷诺数的增大而增强。姜波等[12]数值模拟了振动圆柱外的传热特性，发现振动圆柱传热效果随着振动频率和振幅的增大而增强。谢公南等[13]数值研究了渐扩渐缩波纹管通道内周期性脉动气流引起的强化传热特性，发现传热系数随着雷诺数Re、频率f和压力幅值prms的增大而增大。周国发等[14]对脉动流诱导换热管振动的热-流-固耦合强化传热机制进行了数值研究。研究发现，强化传热强度随脉动频率的增大而加强，且近壁区域形成的内涡微流加强了管壁附近流体的混合对流换热。李国能等[15-16]实验研究了不同雷诺数、脉动频率和压力振幅的脉动流中平行圆柱体的对流换热问题，发现相对努塞尔数与频率、雷诺数成反比，与压力幅值成正比。刘健华等[17]数值研究了管内壁面振动对传热的影响，发现存在临界振动频率使传热效果最佳。

综上所述，国内外通过研究不同参数下圆柱进行自激振动或脉动流横掠圆柱时的传热特性发现：传热效果与雷诺数、压力幅值等表征振荡流强度的参数成正比；而与频率的关系存在不确定性，如文献[11]～文献[14]与文献[15]～文献[16]得到了相反的结论。这是由于对稳定声流强化传热机理缺乏深入认知，而频率决定了稳定声流和自由振荡流的相对强弱。基于此，笔者以某电厂630 MW锅炉中屏式过热器末级换热管为研究对象，研究了不同参数声波在换热管周围形成的稳态声流对传热效果的影响，这丰富了声波强化热、质传输的理论基础。

1 物理模型与控制方程

1.1 几何模型

图1给出了某电厂630 MW锅炉中屏式过热器末级换热管二维结构示意图。换热管外径为d=38.1 mm。如图1所示，换热管受到水平方向声波的作用。

图1 声波作用换热管示意图Fig.1 Schematic diagram of acoustic wave action heat exchanger tube

1.2 控制方程

1.2.1 一阶热黏性方程

为了准确捕捉换热管外的声学行为，需要耦合求解一阶热黏性方程。一阶声场通过耦合求解热力学传热方程、运动连续性方程和动量方程[18]来描述：

(1)

(2)

(3)

式中：λ为流体的导热系数；T0为换热管初始壁温；T1为声波在管壁附近热黏性损耗引起的温度变化；u1、p1分别为一阶流体流速和压力；ρ0为流体静态密度；α为流体的热膨胀系数；γ为比热比；k为等熵压缩率；μB为体积黏滞系数；μ为切变黏滞系数；cp为流体的比定压热容；t为作用时间。

以上一阶场量是由激励源引起的具有谐波依赖性的变量：

(4)

式中：ω1为激励角频率；p10、u10、ρ10和T10为一阶场量的幅值;因子exp(-iω1t)表征流体对激励声场的响应特性。

1.2.2 二阶声流控制方程

基于流体基本方程和传热方程，考虑小振幅(ε<1，其中ε=u10/(ω1d))的情况，利用Nyborg微扰法将流场变量展开到二阶项,可得到稳态声流的控制方程[18-19]：

(5)

ρ0∇〈u2〉=-∇·〈ρ1u1〉

(6)

ρ0cp〈u2〉∇T2=∇·〈λ∇T2〉+Q

(7)

式中：〈〉表示对物理量在整个振荡周期内取时间平均；T2为由边界条件给定的温度；u2、p2分别为二阶流体流速和压力；Q为给定内热源，此处设定为恒定热流。

由式(5)、式(6)可知，一阶场量是驱动二阶场量的源项。式(5)等号右边的一阶场量可视为驱动二阶场量的体积力。式(6)等号右边的一阶场量为驱动二阶场量的质量源。式(7)表示稳定声流与温度场的耦合热动力学方程。

2 数值模型

2.1 模型建立

图2给出了换热管外一阶场和二阶场的数值计算模型。为尽量减小外边界对换热管外声流的影响，设定计算域为边长L=10d=381 mm的正方形。

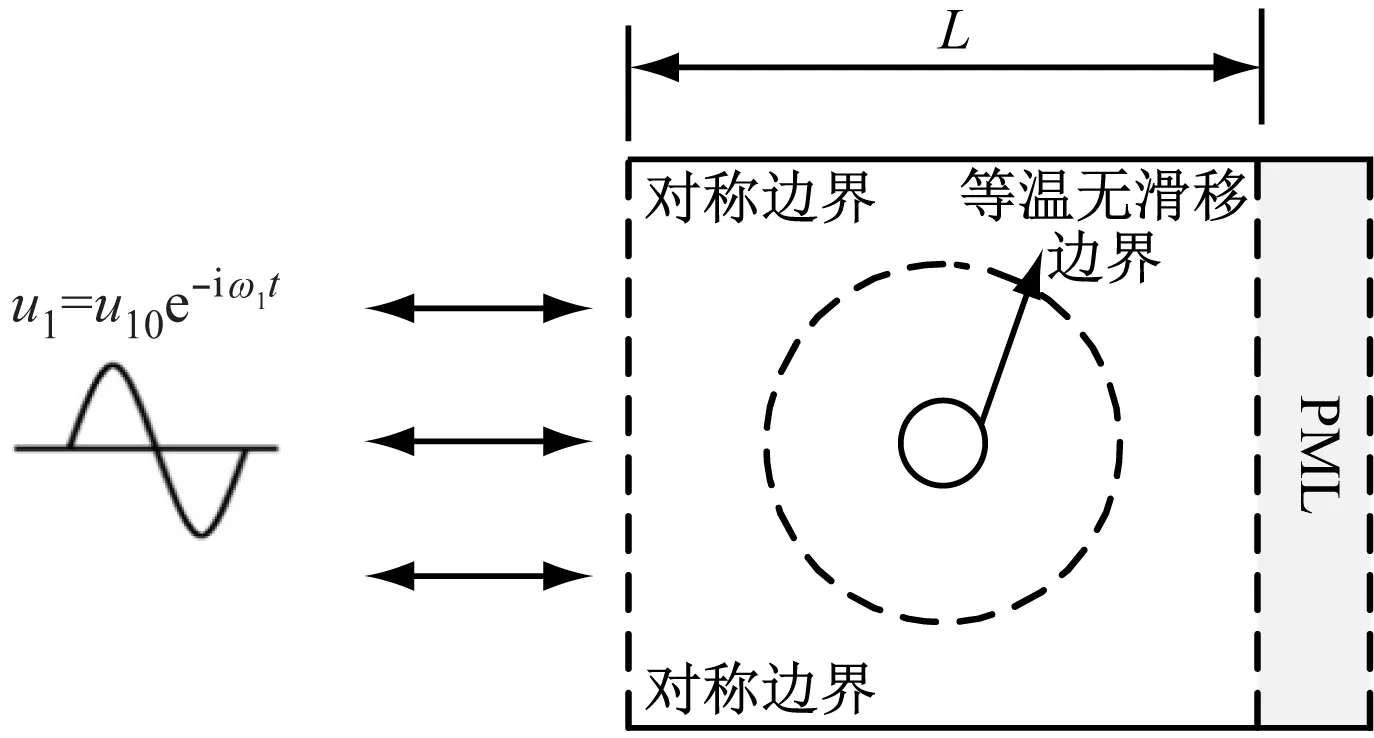
(a) 一阶场计算模型示意图

(b) 二阶声流耦合温度场的数值计算模型图2 数值计算模型Fig.2 Numerical calculation model

图2(a)给出了一阶场计算域边界条件：(1) 上、下侧设定为对称边界；(2) 右侧出口设置为PML边界层，即声波在右侧被完全吸收；(3) 换热管壁面为等温无滑移条件，该边界条件可在换热管壁面附近形成热黏性边界层(即声学边界层)，这也是形成声流的必要条件；(4) 左侧给一个速度边界作为激励源在计算域内形成平面行波场(见式(8))。

ubd=u0e-iω1t

(8)

式中：ubd为边界激励速度；u0为速度幅值。

根据式(8)的速度幅值，可折算为相应的声压级SPL：

(9)

式中：Uref为参考质点振动速度，取4.83×10-8m/s。

结合式(1)～式(4)，图2(a)中的边界条件可完整描述换热管置于平面声波场中诱导的流场特性。

图2(b)给出了声流影响传热的计算域边界条件：(1) 换热管壁设定为恒定热耗率P0；(2) 四周边界都设定为恒温边界T0。结合式(5)～式(7)，图2(b)中的边界条件可完整描述换热管外二阶声流与不均匀温度场的耦合关系。

2.2 网格划分

图3给出了换热管附近的局部网格划分结果。一阶场在声学边界层内的热黏性损耗是形成换热管外声流的关键因素。因此，精确捕捉到声学边界层中的物理场信息是准确模拟换热管外稳态声流的重要条件。声波在换热管附近形成的热边界层厚度δth和黏性边界层厚度δv[18]分别为：

(10)

式中：ω1为激励角频率，ω1=2πf，其中f为激励频率。

由式(10)可知，热黏性边界层厚度与激励角频率成反比。在1 200 ℃、标准大气压的空气介质中，频率为10 Hz的声波在换热管壁面附近形成的热边界层厚度和黏性边界层厚度分别为：δth=3.12 mm，δv=2.72 mm。由此可见，换热管壁面附近需要非常精细的网格控制来捕捉声学边界层内的物理现象。

图3 换热管局部网格Fig.3 Local grid for heat exchanger tubes

在空气介质中，普朗特数Pr=(δv/δth)2<1，这表明热耗散尺度要大于黏性耗散尺度。因此，以黏性边界层厚度δv为基准，在换热管壁面附近生成第一层网格厚度为0.1δv、边界层拉伸因子为1.115、边界层数为12层的自由四边形网格，以完全覆盖声学边界层，而边界层外生成自由三角形网格。通过加密声学边界层外三角形网格，当模型计算域生成网格数大于37 724时，数值解趋于稳定。

计算域内选取1 200 ℃的空气作为计算介质，其主要参数见表1。

表1 介质主要参数Tab.1 Main parameters of calculation medium

2.3 数值计算方法

基于有限元软件COMSOL，采用分离时间尺度的数值方法实现了换热管外稳态声流的精确模拟，并评估了不同参数下声流对传热的影响。图4给出了计算流程图。

图4中，首先通过热黏性声学频域模块求解满足式(1)～式(4)的一阶声场。然后，将得到的一阶场量时均值作为源项代入式(5)、式(6)中，并采用预定义的层流模块求解满足式(5)、式(6)的稳态声流控制方程，由此可计算出没有耦合温度场的声流。最后，同样将得到的一阶场量作为输入源，将预定义的层流模块、传热模块进行耦合后，求解式(5)～式(7)，从而评估声流对传热的影响。

图4 计算流程图Fig.4 Calculation flowchart

2.4 数值方法验证

为验证本文数值方法的可行性，图5给出了圆柱处于驻波声压波节位置时，归一化声流速度的数值解与相应解析解的对比曲线，其中θ为方位角。归一化声流速度U定义为径向r上的声流速度除以声流速度最大值后得到的分布特征，U=u2/max(u2)。

(a) θ=0°

(b) θ=45°图5 数值解与相应解析解的对比Fig.5 Comparison of numerical solution and corresponding analytical

激励频率f=1 000 Hz，声压级为103 dB(速度幅值u0=0.01 m/s)。在满足小振幅(ε≪1)和声波波长L≫d的条件下，Lee等[20]给出了驻波声场中二维圆柱体边界层外声流的解析解。Lee的解析解表明，当圆柱体处于声压波节位置时，边界层外的声流结构关于圆柱呈轴对称均匀分布。

由图5可知，采用分离时间尺度得到的数值解与相应的解析解基本一致，这表明该数值方法可用于计算换热管外的稳态声流。观察图5可知，在靠近管壁一定距离(r=0～15 mm)的数值解和解析解吻合度较高，这表明在靠近换热管壁面声学边界层附近的二阶声流得到了精确求解；而随着r增大，二者的吻合度降低，这是因为Lee的解析解是在无限计算域中得到的，而本文数值解是在有限计算域内计算得到。计算表明，计算域越大，声流的涡中心离圆柱越远，相反，计算域变小，声流的涡中心向着圆柱靠近。然而，只要计算域的尺度远大于换热管壁面附近的热黏性耗散尺度，这并不影响对声流特性的分析。此外， Lee的解析解是在满足ε≪1和L≫d的严格条件下得到的，而数值解对振幅参数ε没有严格的限制，但同样要满足ε<1和L≫d的条件。当需要考虑ε≥1的条件时，声流控制方程式(6)、式(7)不再适用，而需考虑更高阶的物理量[5]。综上所述，本文数值方法直接求解小振幅(ε<1)声流控制方程式(5)和式(6)，可以完整描述换热管外的声流特性。

3 声流强化对流换热的数值分析

3.1 声压级对耦合场特性的影响

为清晰呈现换热管热黏性边界层中的内涡流结构，选取激励频率f=10 Hz。为考察声压级的影响，根据式(9)，将选择的速度幅值u0折算成相应的声压级。图6给出了不同声压级下声流和温度场耦合后的场分布特性和以最大声流速度u2max表征的声流强度随声压级的变化规律，为方便比较耦合场特性，在图6(a)～图6(c)中，上半部分给出了耦合场中的声流流线图，下半部分给出了耦合场中温度场云图。

由图6(d)可知，声流强度随着声压级的增大呈指数增大。SPL取103 dB、117 dB时声波在换热管周围形成的最大声流速度分别为0.089 mm/s和2.23 mm/s，因此声压级较小时，该强度的声流运动对换热管外温度场的影响几乎可忽略，温度场基本呈均匀分布(见图6(a)和图6(b) )；SPL=123 dB时声波引起的声流速度最大约为20 mm/s，因此声压级较大时该强度的声流运动对换热管外的温度场产生较大影响，使温度场呈不均匀分布(见图6(c))。以上分析表明，低强度(SPL<123 dB)声波形成的弱声流运动对温度场的影响可以忽略，而高强度声波(SPL≥123 dB)形成的激烈声流运动对换热管外温度场具有决定性作用。

(a) SPL=103 dB

(b) SPL=117 dB

(c) SPL=123 dB

(d) 声流强度随声压级的变化规律图6 声压级对耦合场特性的影响Fig.6 Effect of sound pressure level on coupling field characteristics

此外，对比图6(a)～图6(c)可知，随着声压级的增大，换热管外黏性边界层中的内涡流在声波作用方向受到“挤压”而发生了流型畸变，该流场结构的改变使换热管左、右侧附近的流体温度降低。

3.2 激励频率对耦合场特性的影响

对于给定声压级SPL=123 dB，图7给出了不同激励频率下声流和温度场耦合后的场分布特性及声流强度随激励频率的变化规律。

由图7(d)可知，换热管外的声流强度随着激励频率的增加呈指数形式减小。对比图7(a)～图7(c)可知，换热管热黏性边界层中的内涡流尺度随着激励频率的增大快速减小，而边界层外的涡流尺度随之增大。低频声波可在换热管外较厚的热黏性边界层中形成强烈的涡流，如图7(a)所示，f=10 Hz、SPL=123 dB的声波在换热管外形成的最大声流速度约为9.06 mm/s，这时换热管附近的温度场主要受到内涡流流场特性的影响。此外，通过边界层内、外涡流的流线密度也可看出边界层内的涡流强度要大于边界层外的涡流强度。在图7(a)中，内涡流在水平方向上的“冲刷”效应使换热管左、右两侧附近的流体温度较低，而在垂直方向受到内、外涡流的共同影响。高频声波在换热管外形成的外涡流是影响温度场的主要因素，因为高频声波在换热管壁面形成的热黏性边界层厚度极薄，使换热管散失的热量快速穿过该边界层，这时外涡流的流场特性将对换热管外温度场分布起到决定性作用。如图7(b)和图7(c)所示，外涡流在垂直方向上对换热管的“冲刷”效应使换热管上、下两侧的流体温度较低，而换热管的热量在水平方向被背离换热管流动的外涡流带走。

综合第3.1节和本节的分析可知，声压级和激励频率是影响换热管外温度场的重要因素。激励频率决定了内、外涡流的尺度大小和强弱，且内、外涡流总保持着反向旋转；声压级则决定了声流运动的整体强弱。

3.3 声流对局部努塞尔数和平均努塞尔数的影响

为研究声流对换热管传热的影响，设定管壁为恒定热耗率边界条件：

P0=Ah(Twall-Ta)=qA

(11)

式中：P0为热耗率，取为10 W；A为换热管单位长度热流面积，A=πd；q为热流密度；Twall为换热管壁温；Ta为环境温度；h为换热管管壁的局部对流传热系数。

(a) f=10 Hz

(b) f=20 Hz

(c) f=50 Hz

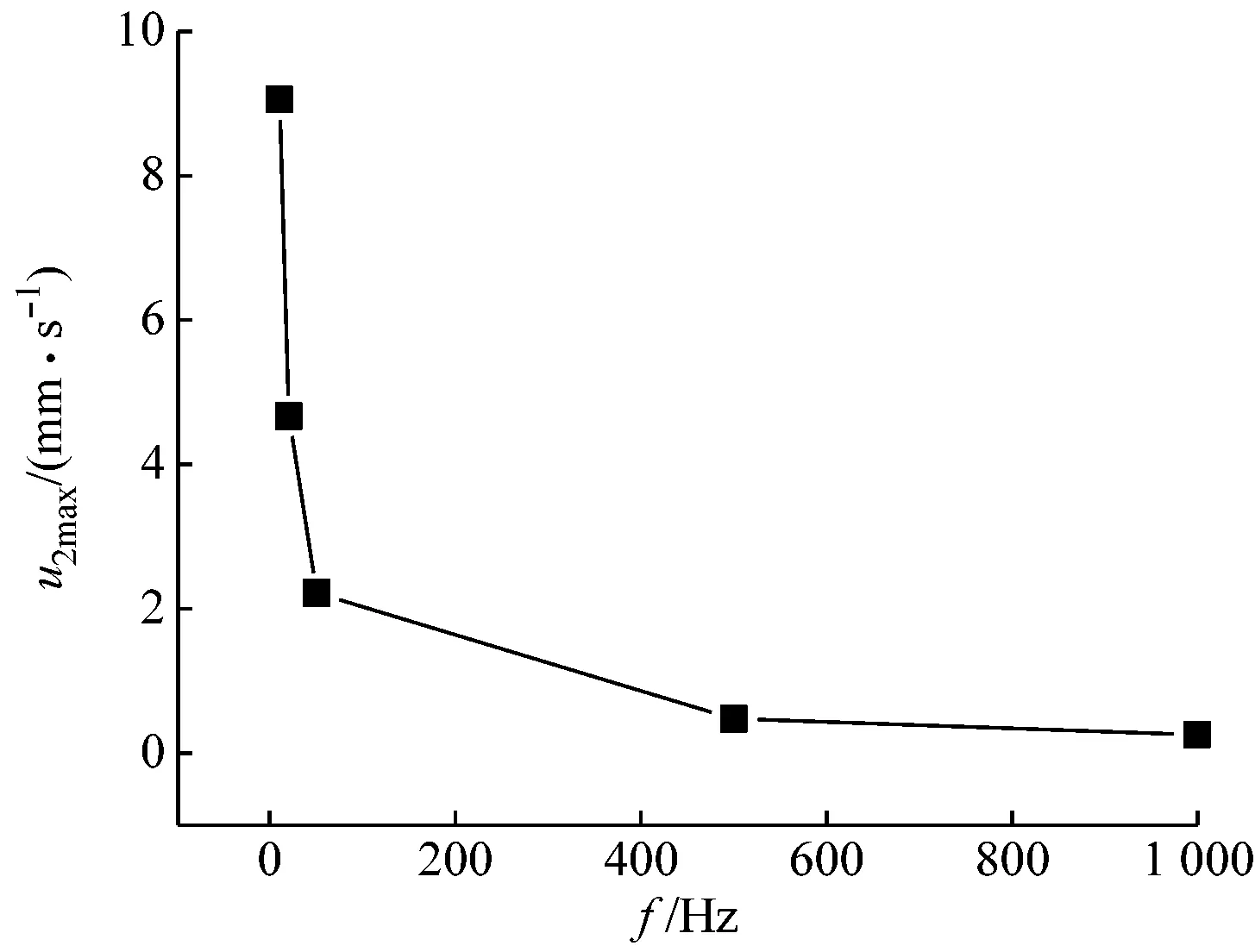
(d) 声流强度随激励频率的变化规律图7 激励频率对耦合场特性的影响Fig.7 Effect of excitation frequency on coupling field characteristics

为描述声流对换热管周围空间的影响规律，式(12)给出了换热管壁面局部努塞尔数Nuθ的定义，表征声流对换热管壁面圆周对流换热的影响，与换热管外的声流特征有关。

(12)

式中：hθ为换热管壁面圆周上的对流传热系数。

(13)

3.3.1 激励频率对换热管换热的影响

根据式(12)和式(13)，图8给出了不同声压级下激励频率对换热管局部努塞尔数和平均努塞尔数的影响曲线。

由图8(a)～图8(c)可知，对于给定声压级，激励频率对换热管局部努塞尔数Nuθ的分布特性具有重要影响。激励频率较低时，如f=10 Hz，换热管局部努塞尔数在90°和270°方位角下出现峰值，这是因为低频声波在换热管外产生尺度较大、强度较强的内涡流，这些内涡流在平行于声波作用方向上对换热管左、右侧产生“冲刷”效应；而在激励频率较高时，如f≥100 Hz，换热管局部努塞尔数在0°和180°方位角下出现峰值，这是因为高频声波在换热管外产生的内涡流尺度很小、强度很弱，这时换热管受到外涡流在x=0方向上对换热管上、下两侧的“冲刷”效应。从图8(a)～8(c)还可知，对于给定声压级，高频声波对换热管局部努塞尔数的影响很小。

3.3.2 声压级对换热管换热的影响

图9给出了不同激励频率下声压级对换热管局部努塞尔数和平均努塞尔数的影响曲线。

由图9(a)～图9(c)可知，对于给定激励频率，不同声压级对换热管局部努塞尔数Nuθ分布的影响规律类似。声压级越大，换热管局部努塞尔数越大，而较低的声压级对换热管的传热效果并不显著，如SPL取103 dB、113 dB和117 dB时对应的曲线。由式(9)可知，低声压级引起的介质速度振幅很小，即对介质的扰动不够强烈。而高声压级可在换热管外形成强烈的声流扰动，这加强了换热管与周围介质的换热过程。因此，增大声压级是强化换热管换热的直接有效手段。

(a) SPL=117 dB

(b) SPL=123 dB

(c) SPL=127 dB

由图9(d)可知，换热管平均努塞尔数随着声压级的增大呈指数形式上升，且激励频率f越低，平均努塞尔数越大。这也同样证明了低频高强度声波是强化换热管传热过程的重要手段。

(a) f=10 Hz

(b) f=100 Hz

(c) f=500 Hz

4 结 论

(1) 对于低频声波，局部努塞尔数的分布规律由换热管周围的内涡流流场特征决定，如在90°和270°方位角上出现局部努塞尔数的峰值；而对于高频声波，局部努塞尔数的分布规律由换热管周围的外涡流流场特征决定，如在0°和180°方位角上出现局部努塞尔数的峰值。换热管周围内、外涡流的流场特征共同确定了换热管外的温度场。

(2) 对于给定声压级，声流强度和平均努塞尔数随着激励频率的增大呈指数形式快速减小；对于给定激励频率，声流强度和平均努塞尔数随着声压级的增大呈指数形式迅速增大。

(3) 激励频率和声压级是影响换热管对流换热特性的主要因素。低频高强度声波可在换热管热黏性边界层内、外形成强烈的声流扰动，极大地强化了换热管的热传输过程。此外，增大声压级是强化换热管热传输过程最直接有效的手段。