类椭球体放矿理论移动过渡方程的研究
2021-08-23李金河范才兵郭进平
李金河 范才兵 郭进平
(1.中钢矿业丰宁万隆矿业发展有限公司;2.中钢矿业开发有限公司;3.西安建筑科技大学资源工程学院)
类椭球体放矿理论是在实验观察、回归分析和理论研究的基础上创立的,其包含了椭球体放矿理论的部分合理内核(如移动迹线方程、移动过渡方程、相关关系方程),解决了椭球体放矿理论存在的问题和不足(如放出体形、移动边界、速度场和密度场)[1],拓展和发展了椭球体放矿理论。
移动过渡方程是放矿理论的重要基础方程,是评价一种放矿理论是否正确、完备的重要指标[2]。为夯实理论基础,特对类椭球体放矿理论的移动过渡方程建立的基础以及建立过程进行深入研究。
1 移动过渡方程建立的基础
类椭球体放矿理论的移动过渡方程是建立在移动过渡原理和质量守恒定律的基础上的。
1.1 移动过渡原理
移动过渡原理是放矿理论最重要的基础。前苏联学者Г.М.马拉霍夫根据实验认为,放矿中存在放出体过渡和等速体(等速度面)过渡,并根据等速度体过渡建立了椭球体放矿理论[3]。前苏联学者B.B.库里柯夫根据实验认为,放矿过程中只存在放出体过渡,并在放出体过渡的基础上,建立了现行的椭球体放矿理论。许多研究者通过实验证实了B.B.库里柯夫的观点是正确的。因此,移动过渡原理被准确描述为放出体移动过渡原理。
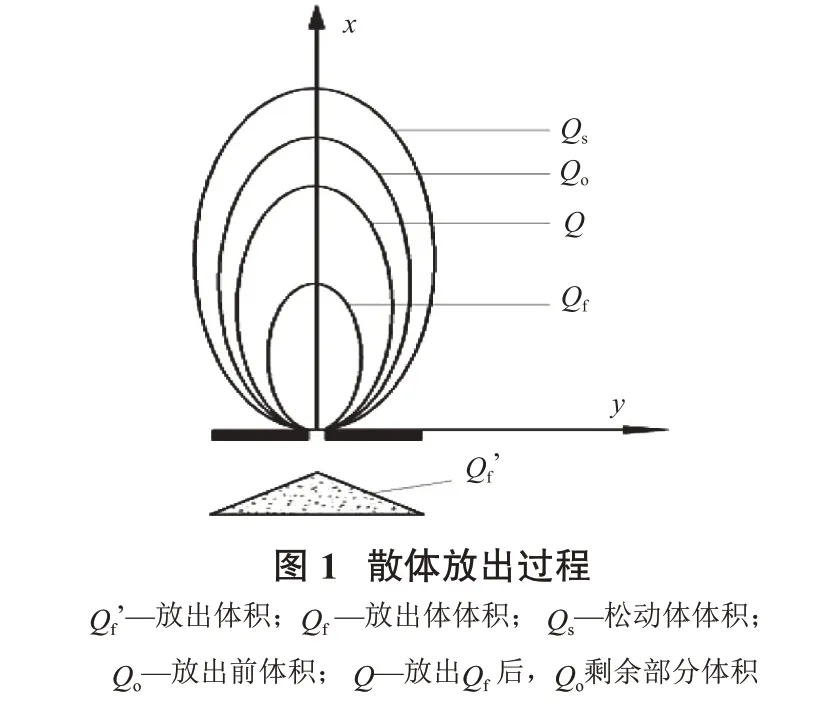
如图1所示,设Q0空间中的散体颗粒放出放出体Qf后移动到Q(即Q0中未放出的散体占据空间位置Q),这种移动过渡关系包括以下内容:
(1)整体过渡。即Q0内所有散体,除放出体Qf内的颗粒已放出,其余全部散体颗粒都移动到了Q内。
(2)移动体表面整体过渡。即Q0表面那些颗粒都移动到了Q表面上。
(3)颗粒间相关位置不变化的整体过渡。即颗粒间位置不互换,颗粒顺次移动(位置坐标比例不变)。
(4)体形不变整体过渡。即类椭球体的体形不变,决定体形的参数不变。
1.2 质量守恒定律
质量守恒定律是建立移动过渡方程的基础,对于散体场应用质量守恒定律的条件为
(1)散体场为无源场,即散体场中无其他散体源;
(2)散体场底部的放出口是唯一的,散体场中无任何其他放出口。
2 理想散体的移动过渡方程
研究散体放出过程中的质量变化,根据质量守恒定律,可建立散体移动过渡方程的质量平衡方程如下。

式(1)、式(1′)对于理想散体和实际散体均适用。式中,Q0为散体放出前的散体体积;Qf为散体放出体体积;Q为放出Qf时,中Q0剩余散体颗粒在散体场中的散体体积;ρ为散体移动范围内的密度;ρa为散体放出前的初始密度;ρCQ为放出散体Qf时,Q中散体的平均密度。
对于理想散体有二次松散系数η=1,散体密度场为均匀场和定常场,即散体放出前及散体场中各处密度均相等,且不随时间变化。同时,由于无二次松散现象,因此当散体放出开始时,散体场中移动范围内的所有散体颗粒都同时开始移动,无移动滞后现象。故有

式(2)代入式(1′),整理变换得:

式(3)即为类椭球体放矿理论理想散体的移动过渡方程[4]。
3 实际散体质量平衡状态分析
对于实际散体,有二次松散系数η>1,散体密度场在放出前为均匀场和定常场。在放出开始后的放出过程中,由于二次松散使移动范围内各处的密度随坐标位置及时间而变化,移动范围内的密度场为非均匀场和不定常场,但移动范围之外密度仍然保持不变,为均匀场和定常场。
可根据Q0表面颗粒的状态划分出实际散体不同的质量平衡状态。
3.1 Q0表面颗粒静止不动(静止状态)
当放出体Qf<Q0C时,此时Qs<Q0,其质量平衡方程为
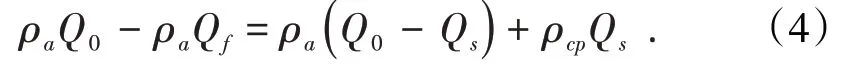
整理得到:

式中,Qs为对应于放出体Qf的松动体体积;C为松动范围系数,;ρcp为松动体Qs内的平均密度,ρcp=ρaη[6]。
式(4′)为Qf<Q0C时的质量平衡方程。
由式(4′)可知,此时Q0表面颗粒静止不动,Q0与Q、Qf不存在函数关系。
3.2 Q0表面颗粒即将投入运动(临界状态)
当放出体Qf0=Q0C时,此时Q0=Qs=Q,Q0表面颗粒正处于松动体边界上,虽然静止不动,但即将投入运动,处于临界状态,此时质量平衡方程为

或
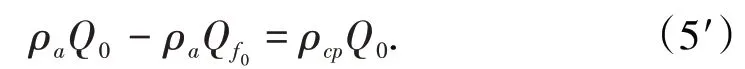
当Q=Qs=Q0时,有ρCQ=ρCP,故由(1)式得:
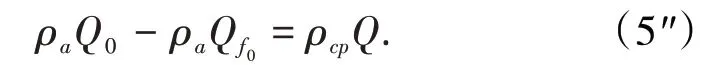
式(5)、式(5′)、式(5")为Q0表面颗粒处于临界状态(静止但即将投入运动)的质量平衡方程。
3.3 Q0表面颗粒投入运动
当放出体Qf>Q0C时,此时Qs>Q0,因此Q0表面颗粒在移动范围内向下移动。此时的质量平衡方程为(1)式或(1′)式。
将式(5′)代入式(1)或式(1′)得:
整理得:

式(6)或式(6’)也为Q0表面颗粒投入运动(移动状态)后的质量平衡方程,式(6)实际是式(1)的另一种表达形式。由式(6′)及式(4′)、式(5′)可知,只有当Qf≥Qf0,即Qf≥Q0C时,Q0和Q的函数关系才存在,故Qf的取值范围为Q0C≤Qf≤Q0。
4 实际散体的移动过渡方程
4.1 密度方程
类椭球体理论经实际观察和研究,建立了散体放出过程中移动范围内的密度方程:

式中,ρ0为放出密度;α为密度变化系数,是与静止密度(处室密度ρa)和放出密度ρ0有关常数;ρ为移动范围内任一点的密度。
式(7)经检验符合实际,且与速度方程一同通过了移动连续性的理论检验,可以认为是类椭球体理论的理论方程[5]。
4.2 移动体平均密度ρCQ计算
根据类椭球体放矿理论的密度方程,计算移动体Q内的平均密度ρCQ。

式(8)、式(8′)即为ρCQ的计算式。
4.3 类椭球体放矿理论实际散体的移动过渡方程
4.3.1 实际散体的质量平衡方程
将式(8′)代入式(1)和式(6),得

式(9)变换整理得:

或
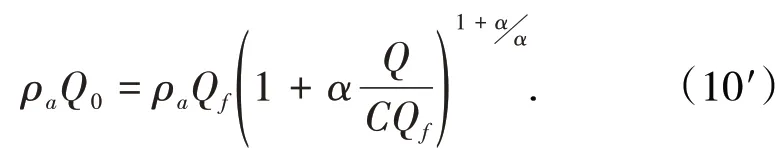
式(10)、式(10′)为实际散体的质量平衡方程。
4.3.2 实际散体的移动过渡方程
对式(10)、式(10′)经变换整理得:
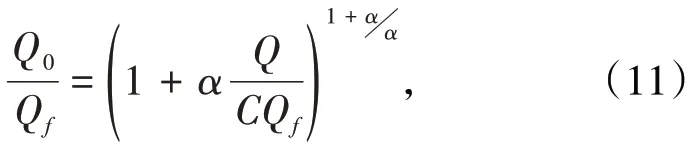
或

式(11)、式(11′)为实际散体的移动过渡方程。
式(11)、式(11′)经变换整理可表达为

或
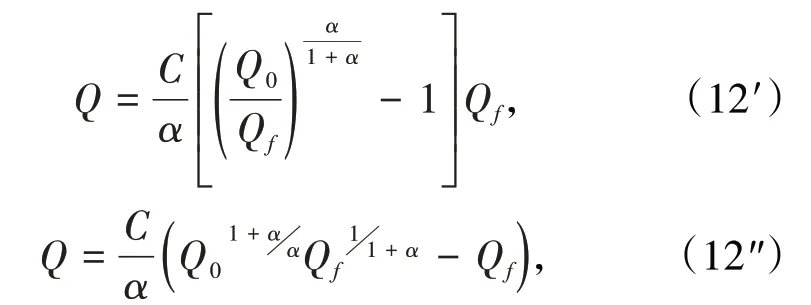
式(12)、式(12′)、式(12")也为实际散体的移动过渡方程。
4.3.3 实际散体移动过渡方程的讨论
(1)当放出体Qf<Q0C时,Qs<Q0,此时,Q0表面颗粒静止不动,由式(4)和式(4′)式知,Q和Q0、Qs不存在函数关系,因此,移动过渡方程式(11)、式(11′)、式(12)、式(12′)不反映Qf<Q0C时的状态,移动过渡方程式(11)、式(11′)、式(12)、式(12′)中Qf的取值范围是Q0C≤Qf≤Q0。
(2)当Qf=Q0,由式(12′)可知Q=0,即Q0表面颗粒全部放出,Q变为零。
(3)当Qf=Q0C时,由式(12′)可知:
Q=CQf=Q0,即Q0表面颗粒即将投入运动,处于临界状态。
(4)当η=1时,根据η=可知:α→∞,此时,代入式(12′)得:

式(13)与式(3)完全相同,为类椭球体放矿理论理想散体的移动过渡方程,因此,理想散体的移动过渡方程是实际散体移动过渡方程η=1的特殊方程。
5 结 论
(1)移动过渡原理和质量守恒定律是类椭球体放矿理论移动过渡方程建立的基础。
(3)实际散体移动过渡方程中,Q0表面颗粒有静止状态、极限状态和移动状态3种质量平衡关系。
(5)类椭球体放矿理论理想散体的移动过渡方程是Q=Q0-Qf,它是实际散体移动过渡方程当η=1时的特殊方程。
