基于迭代动态初始解的水电站发电流量计算方法研究

胡 志 鹏， 吴 莹

(中国电建集团成都勘测设计研究院有限公司，四川 成都 610072)

0 引 言

水电站短期优化调度是水电站水库发电调度的重点研究领域，也是实现水能资源高效利用的关键[1]。对于水电站短期优化调度研究，国内外相关学者主要集中在相关数学模型以及模型的相关求解方法的研究上。在数学模型研究方面，主要变化由单一水电站水库过渡到水库群、单目标转变为多目标模型。模型类型主要是随机动态规划模型[2]、确定性动态规划模型[3]以及模糊优选模型[4]等。在数学模型准则方面，单一水电站的数学模型准则主要包括耗水量最小、发电量最大、保证率最大等，而对于梯级水电站(群)的数学模型的优化准则来说，一般包含有水电站耗能量最小、机组发电量最大[5]等。在对数学模型求解方面，传统求解方法包括有等功率法、等微增率法、运行特性图解法、分支定界法、线性规划法、动态规划法[6]、进化算法[7]等。水库调度方程组的发电流量迭代求解是水电站水能计算的核心环节[8]。针对发电流量迭代计算的相关理论与方法研究在文献中极为少见，亟待深入探索和研究。

传统迭代算法计算机组发电流量时常出现迭代次数过多，迭代不收敛等现象。迭代次数过多限制了收敛速度，对计算效率不利，迭代不收敛则会导致计算结果异常，严重影响水库调度决策[9]。在迭代算法中，迭代因子的初始假设值及迭代方式是制约迭代收敛及收敛速度的关键因素，而对于迭代初始值的假定多具有随意性。本文针对这一问题，以机组发电流量计算影响因素为对象进行研究，提出一种在实际工况下的机组发电流量隐函数形式，并基于发电流量计算影响因素拟提出水电站机组发电流量迭代动态初始解函数式，以该函数计算值作为发电流量迭代计算的初始值。实例应用表明，该方法能够较好提高迭代计算效率且方法简单有效。

1 常规发电流量迭代算法

水电站机组发电流量的计算如公式(1)所示。

Qfd,i(t)=Pi(t)/(9.81ηTηgHi(t))

(1)

式中ηT、ηg分别为水轮机效率和发电机效率；Qfd,i(t)、Hi(t)、Pi(t)分别为第i台机组t时段的耗流量(m3/s)、机组净水头(m)以及出力(kW)。

水库水量平衡公式(2)。

(2)

式中V(t)、V(t+1)分别为t时段初、末库蓄水量(m3)；Qin(t)、Qqs(t)分别为t时段平均入库流量和弃水流量(m3/s)；n为投入运行机组台数；ΔT(t)为时段长。

库容曲线公式(3)。

Zsy(t+1)=fzv(V(t+1))

(3)

式中Zsy(t+1)为t时段末水库上游水位(m)；fzv(V(t+1))表示库容曲线函数。

下游水位流量关系式(4)。

Zxy(t)=fZQ(Qck(t))

(4)

式中Zxy(t)为t时段下游平均水位(m)；fZQ(Qck(t))表示下游水位流量关系函数。

在水电站短期优化调度中，在已知水电站初始计算条件(包括时段初上游水位、入库流量以及各台机组出力等)由出力推求机组发电流量的一般步骤如下：

(1)假设t时段第i台机组的发电流量Q0,i(t)；

(2)计算相应机组水头损失ΔHi(t)；

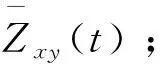
(5)判断第i台机组发电流量迭代计算的收敛性，若|Q0,i(t)-Qfd,i(t)|>ε(其中ε为计算迭代精度)，则表示迭代不收敛，并调整第i台机组发电流量假设值Q0,i(t)返回步骤(2)重新计算，若收敛则迭代结束，由此计算得到第i台机组在t时段的发电流量。

上述对机组发电流量的迭代计算[10]中决定迭代计算次数与效率的一个重要因素就是在进行迭代计算时给发电流量所赋予的初始值Q0,i(t)。因此，在每次迭代计算时，对迭代计算的初始赋值尤为重要。由于水电站机组发电流量不仅与其面临时段的水库水位有关，并且还与计算当前时段的工作状态有关，若能将各台机组的发电流量假设值Q0,i(t)设定为一动态值，其数值大小根据该计算的初始条件而定，因此，可在最大程度上接近迭代计算真值。寻求该方法可以较好地反映不同水电站耗流量大小的真实状态，也能极大地减少迭代计算，提高水电站厂内实时经济运行计算效率，对于水电站的调度运行具有重要的意义[11]。

2 影响发电流量的因素

根据水库水量平衡以及上下游水位库容、水位流量关系，将式(1)展开推导可得到机组出力公式(5)。

(5)

式中α为水头损失系数，其余变量同前所述。

水轮机效率ηT与机组出力Pi(t)、水头之间具有多值非线性函数关系[12]，发电机效率ηg与出力Pi(t)具有非线性函数关系，并由式(5)可知，机组发电流量是关于水库水位、出力以及入库流量为因变量的复合函数，其大小受水库当前水位、水电站机组出力以及入库流量的影响，如式(6)。

Qfd,i(t)=F[Zsy(t),Pi(t),Qin(t)]

(6)

在推导式(5)中，下游水位受水电站总的出库流量(含弃水流量)决定，对于各台机组在承担不同负荷条件下其耗流量也是不同的，为了研究单台机组的发电流量计算方法，本文在进行上述处理时可作一假设：假定在同一初始水位和入库流量条件下，水电站时段总出力均分到投入运行的各台机组，则各机组此时的发电流量和机组水头值相等。根据假定，式(5)可推导转化为式(7)。

-f(n×Qfd,i(t))-αQfd,i(t)2

]

(7)

式中变量同前所述。

3 入库流量与发电流量的关系

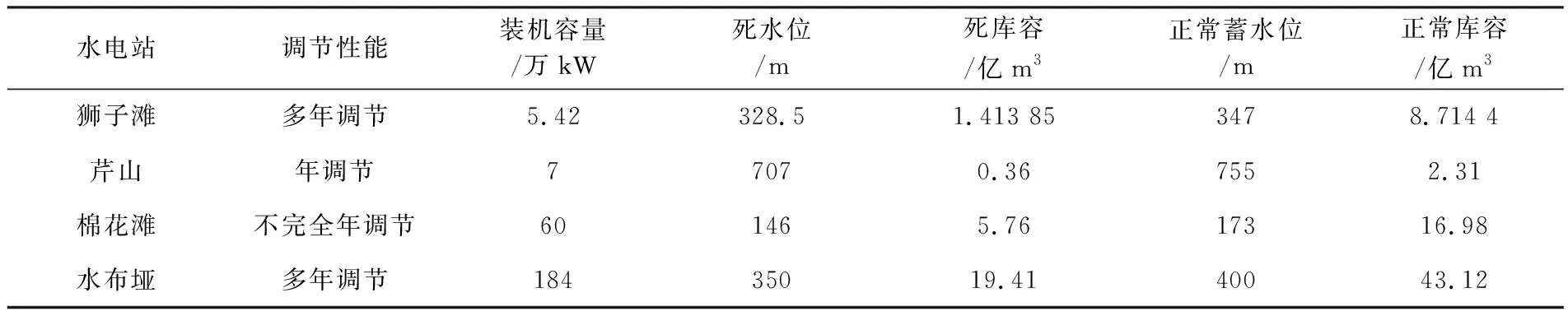
表1 水电站特征参数值表

通过拟合入库流量与发电流量，分析得到两者具有一定的指数函数形式关系，其形式如式(8)所示。

Qfd,i(t)=Qin(t)exp(K)

(8)

式中K为关联参数，其余变量同前所述。

以入库流量Qin的自然对数lnQin为横坐标，发电流量Qfd与入库流量Qin之比的对数ln(Qfd/Qin)为纵坐标作出图1所示的关系图，从图中可以看出两者具有较好的线性关系。对于短期实时调度而言，水库时段初、末的水位变化不大，而水轮机的型式、尺寸在进行计算耗流量时是确定的，运行工况是根据机组在时段内某一水位条件下承担负荷所决定的。水库在不同的入库流量情况下，由水量平衡原理可知水库上下游水位会受入库流量的影响。对于水电站弃水流量可简化忽略不计，入库流量对机组发电流量的影响表现在改变时段内的发电水头，入库流量越大，机组承担的某一出力下所需要发电流量就越小。且该影响取决于水电站运行初始条件，而水电站机组出力与机组耗流量、水电站机组净水头之间具有隐性非线性函数关系。由图1所得到的关系，可将水库上游时段初水位与单台机组出力作为计算前提初始条件，将入库流量与机组发电流量建立单一变量函数关系，并按图1线性关系进行拟合得到式(9)所示函数。

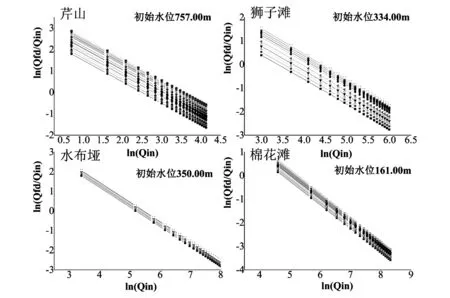
图1 相同初始水位不同机组出力条件下入库流量与发电流量关系图

ln(Qfd/Qin)=aln(Qin)+b

(9)

式中a、b分别为线性拟合得到的一次项和常数项系数；Qfd、Qin分别为单台机组发电耗流量(m3/s)与对应时段的入库流量(m3/s)。联立式(8)、(9)，推导得到单台机组发电流量计算式(10)，式中各变量如前所述。

Qfd=Qin(a+1)exp(b)

(10)

4 实例分析

水布垭水电站位于湖北省恩施州巴东县境内，水库坝址以上流域面积达10 860 km2，是一座以发电为主，同时具有防洪、航运功能的大型水利枢纽。大坝全长660 m，坝顶高程409 m，最大坝高233 m。水布垭水库特征参数见表1，水电站主要设计参数表见表2。

表2 水布垭电站主要设计参数表

根据水布垭水电站发电流量及机组设计资料，电站从引水洞至尾水出口，单台机组发电流量产生的沿程水头损失和局部水头损失总值按式(11)计算。

ΔH=3.242×10-5×Q2

(11)

式中Q为机组流量，单位m3/s；ΔH为沿程和局部水头损失，单位m。

以5 m为步长将上游初始水位从死水位离散至正常蓄水位，水电站机组出力从保证出力310 MW(单台机组)离散至装机出力1 800 MW并考虑对应水头下的预想出力，入库流量的离散范围根据水布垭电站实际测得的流量资料,由最小值离散至最大值，离散范围为[50 m3/s,2 050 m3/s]。由此求得不同条件下的水电站单台机组发电流量，并按前面所述方法研究发电流量与入库流量的关系。

4.1 参数与水位、出力的函数关系

水轮机的效率值与水轮机出力具有复杂的函数关系，式(5)的具体函数形式也是难以确定的。因此，可将前面lnQin与ln(Qfd/Qin)的关系式中参数与发电流量各影响因素进行定变量拟合。在进行实例计算时，由于水电站出力时段内满足预想出力限制，在低初始水位情况下往往达不到水电站最大出力，为了研究机组在所有出力范围内具有的入库流量与发电流量关系，故选取385.00 m、390.00 m、395.00 m、400.00 m等高水位作为计算初始条件，结果如图2所示。

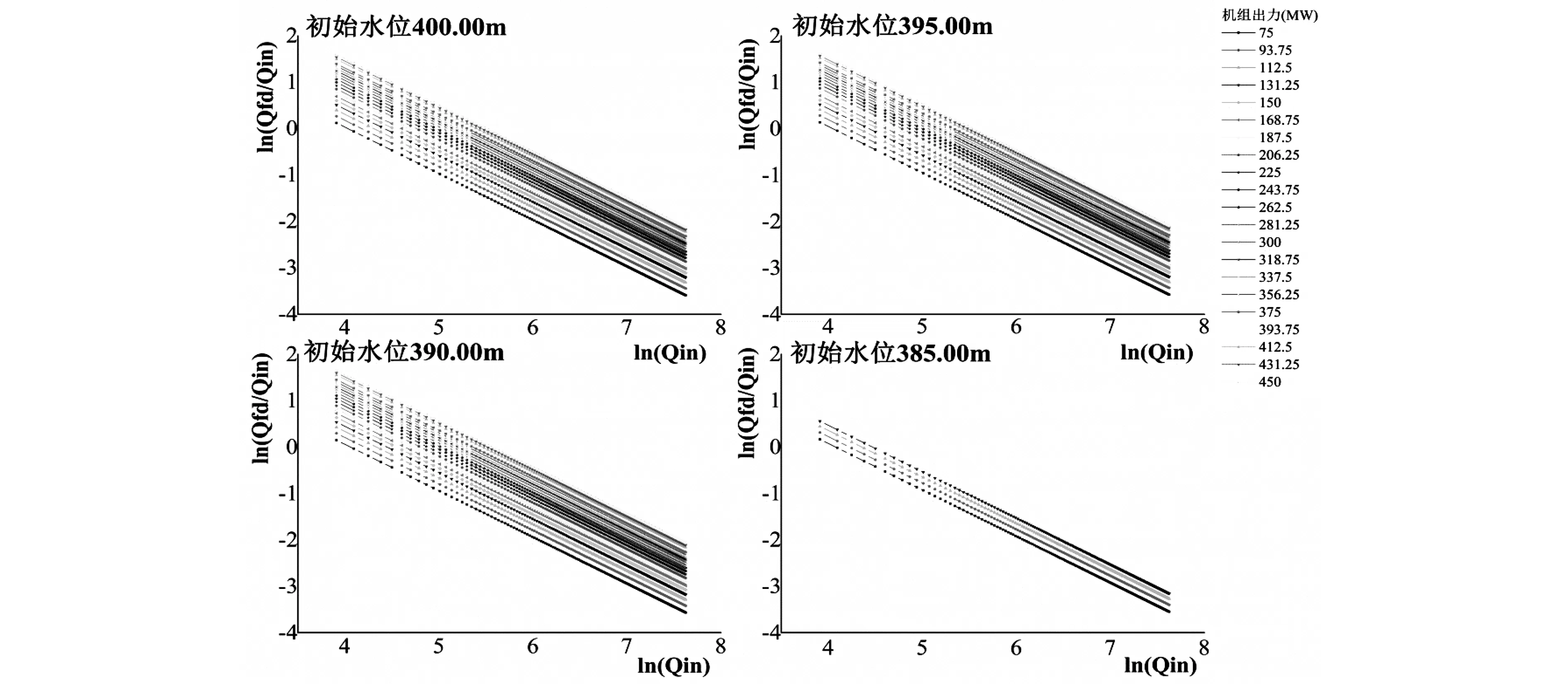
图2 水布垭入库流量与发电流量关系图

以上游初始水位为395.00 m为例，对曲线进行线性拟合，提取曲线拟合得到的函数式中参数a、b的值，结果见表3。

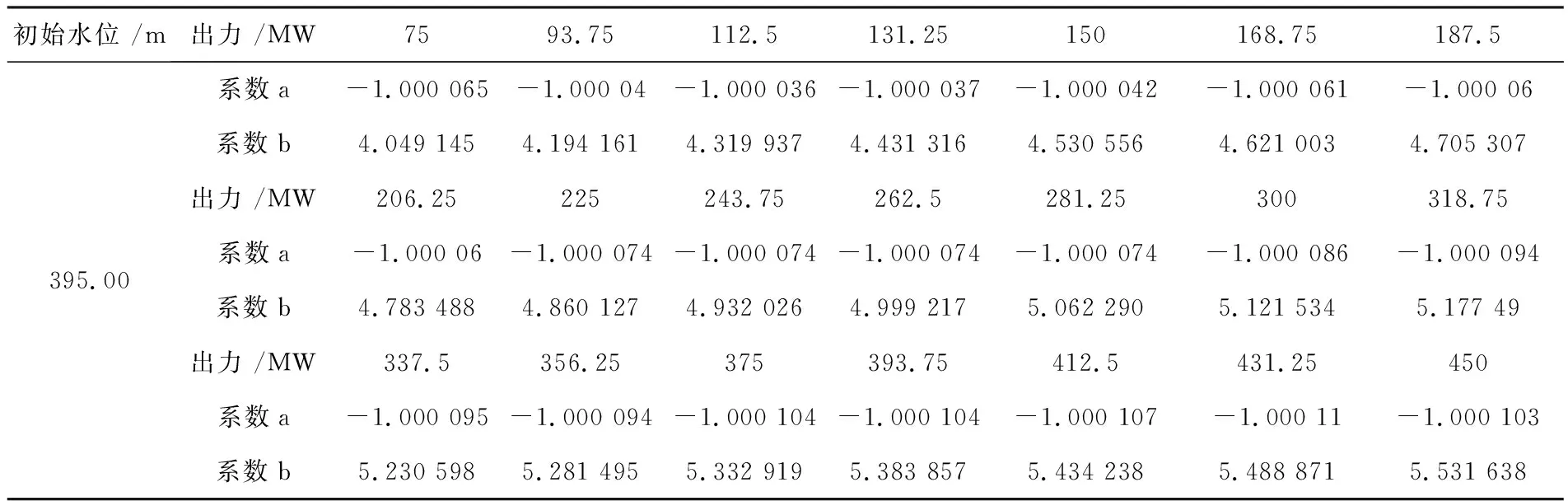
表3 水布垭初始水位395m在不同出力条件下对应的系数a、b值

将一次项系数a和常数项系数b分别与单台机组的出力建立关系，系数a随出力呈线性分布。为在利用发电流量迭代动态初始解函数式计算迭代初始解时计算简单起见，故将系数a与出力进行线性拟合，考虑式(10)中含有自然对数的底以及系数b的点据分布形式，采用自然对数函数f(x)=ln(A+Bx)，拟合曲线得到图3所示结果。

图3 水布垭初始水位395.00 m系数a、b拟合曲线图

将图3中出力随系数a、b拟合曲线的函数式代入式(10)中进行求解，可得到初始水位为395.00 m条件下的发电流量迭代动态初始解函数式，如式(12)所示。

(12)

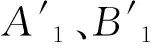
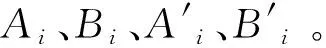
Qfd=Qin(-2×10-7×Pi-0.000 03)×(0.112×Zsy-23.45×(1.6-0.002 5×Zsy×Pi)

(13)

4.2 成果分析

将本文所研究的发电流量计算方法与固定迭代初始解发电流量计算方法在相同初始条件下进行比较。在水布垭计算实例中，以水电站日运行情形下比较两种方法时设定计算初始条件相同，在日调度中设定24个时段不同的水电站负荷值，利用动态规划算法进行机组负荷优化分配，并记录相应耗时与计算耗流量时总的迭代次数，从计算时间与在相同的收敛精度条件下所需的迭代次数分析两种方法的效果。

在水布垭水电站实例中设定情形一：上游初始水位为360.00 m、入库流量为100 m3/s，水电站24个时段中各时段负荷值分别从最小值Nmin=600 MW以步长10 MW离散到最大值Nmax=840 MW。

情形二：上游初始水位为370.00 m、入库流量为100 m3/s，水电站24个时段中各时段负荷值分别从最小值Nmin=700 MW以步长10 MW离散到最大值Nmax=940 MW。

上述基本方法固定迭代初始解均为100 m3/s，结果见表4：在相同的迭代计算收敛精度以及水电站运行情形下，利用本文方式计算机组耗流量能够有效地大幅度减少迭代次数和减少计算时间。

表4 实例计算结果对比表

5 结 语

本文针对在机组出力推求发电流量中迭代初始值的取值随意性，导致存在迭代计算耗时长、效率过低以及迭代不收敛等现象。通过实例研究机组发电流量与入库流量的函数关系，提出了水电站机组发电流量迭代动态初始解的计算方法。在水布垭计算实例中表明：

(1)在本文研究水电站实时运行工况下，采用(12)式所列的机组发电流量隐函数形式计算得到的迭代初始值，能够最大限度地接近迭代计算收敛值，减少迭代计算时间。

(2)依据多组计算数据，以拟合曲线的方式加以确定的系数a能反映出入库流量及对应时段初始水位对机组发电流量的影响程度；系数b反映出时段机组的出力与初始水位对发电流量的影响程度。

(3)实例计算结果表明，本文方法能够较好地提高计算效率且方法简单有效，为水电站短期优化调度中由出力推求发电流量提供了新的方法，有效提高水电站(群)短期优化调度效率，加快水库调度决策。

本文所提出的机组发电流量隐函数形式有待在不同规模水电站进一步进行适应性应用研究。此外，局限于待定系数的复杂性，相关物理意义有待分析研究。