供电距离对含水光配电网孤岛初期稳定性的影响研究
2021-08-23温永森周培源王智东罗艺华
王 玕,温永森,周培源,王智东,罗艺华
(1.广州城市理工学院 电气工程学院,广东 广州 510800;2.广东电网有限责任公司韶关翁源供电局,广东 韶关 512026)
0 引言
电力电子技术的日益成熟,使得水力发电,光伏发电得到了更大规模的开发与利用[1-2]。水、光、风、生物质等多种能源互补运行,不仅可以削弱可再生能源的不稳定性与波动性影响问题,还可以提高各能源电站的运行效率[3-4]。2021年3月中共中央总书记习近平强调要构建清洁低碳安全高效的能源体系,提高利用效能,构建以新能源为主体的新型电力系统。以风光水等新能源电站的建设势在必行。
我国南方偏远山区,由于远离主要供电网络,更高质量、更高可靠性供电成为了农村居民最亟待解决的问题。优先依靠当地丰富的自然资源如水力能源、太阳能等构建分布式电源主动配网系统或微电网系统,可有效解决山区居民在区域主供电线路发生故障或检修时的短时供电问题以及供电线路末端的低电压问题[5-8]。不仅有效提高当地居民的用电可靠性,而且可以减少偏远地区长距离的输电损耗。但水力、光伏等分布式电源分散且大量就地接入配电网,一定程度上使得源端和荷端电压频率均出现较大的不确定性,电力系统的运行方式将更加多样化、分散化,这对富含小水电与光伏的配电网稳定性造成了新的挑战[9-11]。
电压稳定与频率稳定是电力系统运行安全、可靠的两个考核重要指标[12]。频率稳定是电力网络安全可靠运行的基本反映,文献[13]搭建了风光储微网发电系统模型,相对于独立的风电与光伏系统,风光互补系统电压及功率波动较小,风光储微网发电系统则能有效改善输出电压及功率波动的问题。但由于储能成本较高,山区风力发电、光伏发电、水力发电多运行在缺少储能的状态下。针对这一情况,文献[14]研究无储能情况下风光微电网孤岛初期幅频特性,仿真结果表明风电孤岛容易出现系统崩溃的现象,风光互补运行具有较好的频率稳定性。文献[15]对风水不同源比下孤网初期的稳定性进行研究,结果表明对比风力发电机组,水力发电机组具有较大的惯量水平。
目前水轮机组与光伏发电并网后系统的孤岛稳定性研究较少,因此本文构建水光并网仿真模型,通过仿真研究的方法,分析源端的接入距离对含水光的配网系统孤岛初期频率稳定性的影响,为山区配网建设提供理论支撑。
1 水光并网系统架构
小水电、光电接入主电网的系统框图如图1所示。光伏发电与水力发电后经变压器升压后传输至负荷端,当光伏发电与水力发电的发电源端功率大于负载时,富余电力通过联络开关送入电网;当光伏发电与水力发电的发电源端功率小于负荷端功率时,不足的功率电网将通过联结开关送入负荷[16]。当电网单线路需检修或线路出现故障时,主动断开联络开关,水力发电、光伏发电与负荷离网后孤岛运行,保障重要负荷的正常供电。

图1 小水电、光电接入配网系统架构图Fig.1 System architecture diagram of small hydropower and photovoltaic access to power grid
1.1 水电并网简化模型
小型水力发电站通过天然水库或自建拦水坝将水流集中后由引水渠引入水轮机组,再由水轮机调速器与励磁系统控制器调节水轮机组发电,后经变压器转换电压,经过输电配电线路后供给用户[17]。小型水力发电并网模型如图2所示。

图2 水力发电简化模型Fig.2 Simplified model of hydropower generation
1.2 光伏并网简化模型
图3为光伏并网模型,由光伏阵列、三电平功率变换器、LC滤波器组成,光伏阵列设定工作在最大功率点工作模式[18]。一定光照条件下,光伏阵列利用光生伏特效应将太阳能转换为直流电能,直流电能通过三电平功率变换器逆变为交流电能,经LC滤波器削弱逆变过程中的谐波分量后并入电网[19]。

图3 光伏并网简化模型Fig.3 Simplified model of photovoltaic grid-connected system
2基于MATLAB的水光并网模型
为深入研究源端供电距离对含水光配电网频率的影响,在Matlab平台上搭建含水力和光伏联合发电的微电网模型如图4,图中包含水力发电模型,光伏发电并网模型,供电线路、负荷、并网开关等[20]。其中光伏发电、水力发电后经过变压器升高电压,然后经过线路给区域负荷供电。仿真初始时,水电光伏并网运行,1 s后并网开关断开,并网开关断开后,孤岛状态下的系统电源与负荷之比为1∶1,仿真总时长为60 s。

图4 小水电、光伏并网模型Fig.4 Small hydropower and photovoltaic grid connection model
3 不同供电距离的仿真分析结果
为了研究系统孤岛的仿真情况,在本地小水电与光电两种电源容量和与本地负荷相等的前提下,通过调整光伏和小水电的接入距离进行仿真,仿真场景如

表1 不同供电距离仿真设置Table 1 Different power supply distance scenarios
场景一模式下,水力发电与光伏发电的供电距离均为4 km。如图5所示,仿真初始系统频率稳定为50 Hz。1 s时并网开关断开,断开后,水光配电网系统为孤岛模式,系统频率快速上升,在8.318 s时到达峰值54.72 Hz,然后频率开始下降,在27.75 s时下降至波谷值49.56 Hz,谷值后开始缓慢上升,最终稳定在50.24 Hz左右。
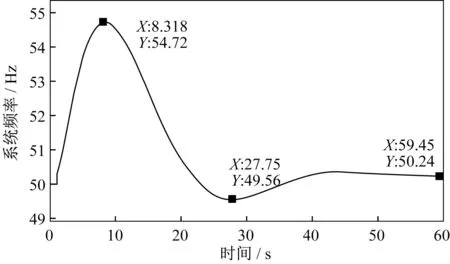
图5 场景1模式下系统频率波形图Fig.5 System frequency waveform in scenario 1
场景二模式下,光伏发电侧的供电距离为4 km,增加水力发电侧供电距离至10 km。如图6所示,仿真初始系统频率稳定为50 Hz。1 s时并网开关断开,断开后,水光配电网系统为孤岛模式,系统频率快速上升,在9.061 s时到达峰值62.63 Hz,然后频率开始下降,在32.33 s时下降至波谷值47.74 Hz,谷值后开始缓慢上升,最终在51.06 Hz上下平稳波动。
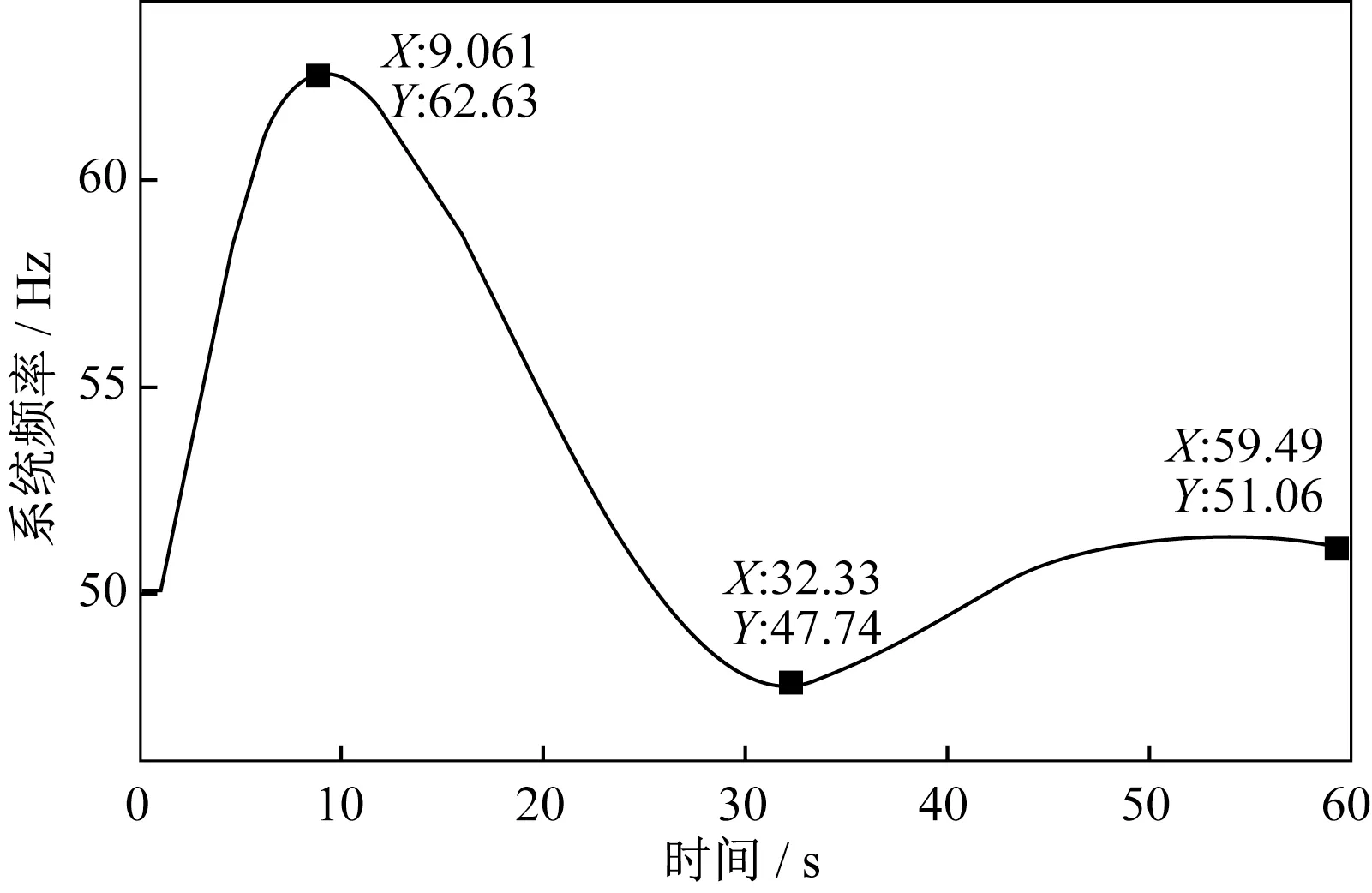
图6 场景2模式下系统频率波形图Fig.6 System frequency waveform in scenario 2
场景三模式下,光伏发电侧的供电距离为6 km,水力发电侧供电距离为8 km。如图7所示,1 s时并网开关断开,水光配电网系统频率缓慢上升,9.13 s到达峰值60.33 Hz,然后频率开始下降,31 s时下降至最小值48.27 Hz,31 s后开始上升,最终在50.74 Hz上下平稳波动。
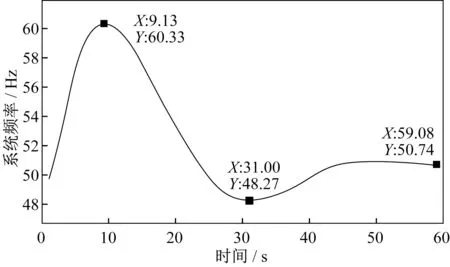
图7 场景3模式下系统频率波形图Fig.7 System frequency waveform in scenario 3
场景四模式下,光伏发电侧的供电距离为8 km,水力发电侧供电距离为6 km。如图8所示,并网开关断开后,水光配电网系统频率快速上升,8.542 s到达峰值57.58 Hz,然后频率开始下降,29.31 s时下降至最小值48.96 Hz,29.31 s后开始缓慢上升,最终在50.43 Hz上下平稳波动。

图8 场景4模式下系统频率波形图Fig.8 System frequency waveform in scenario 4
场景五模式下,光伏发电侧的供电距离为10 km,水力发电侧供电距离为4 km。如图9所示,并网开关断开后,水光配电网系统频率快速上升,8.378 s到达峰值54.72 Hz,然后频率开始下降,27.71 s时下降至最小值49.56 Hz,27.71 s后开始上升,最终在50.24 Hz上下平稳波动。
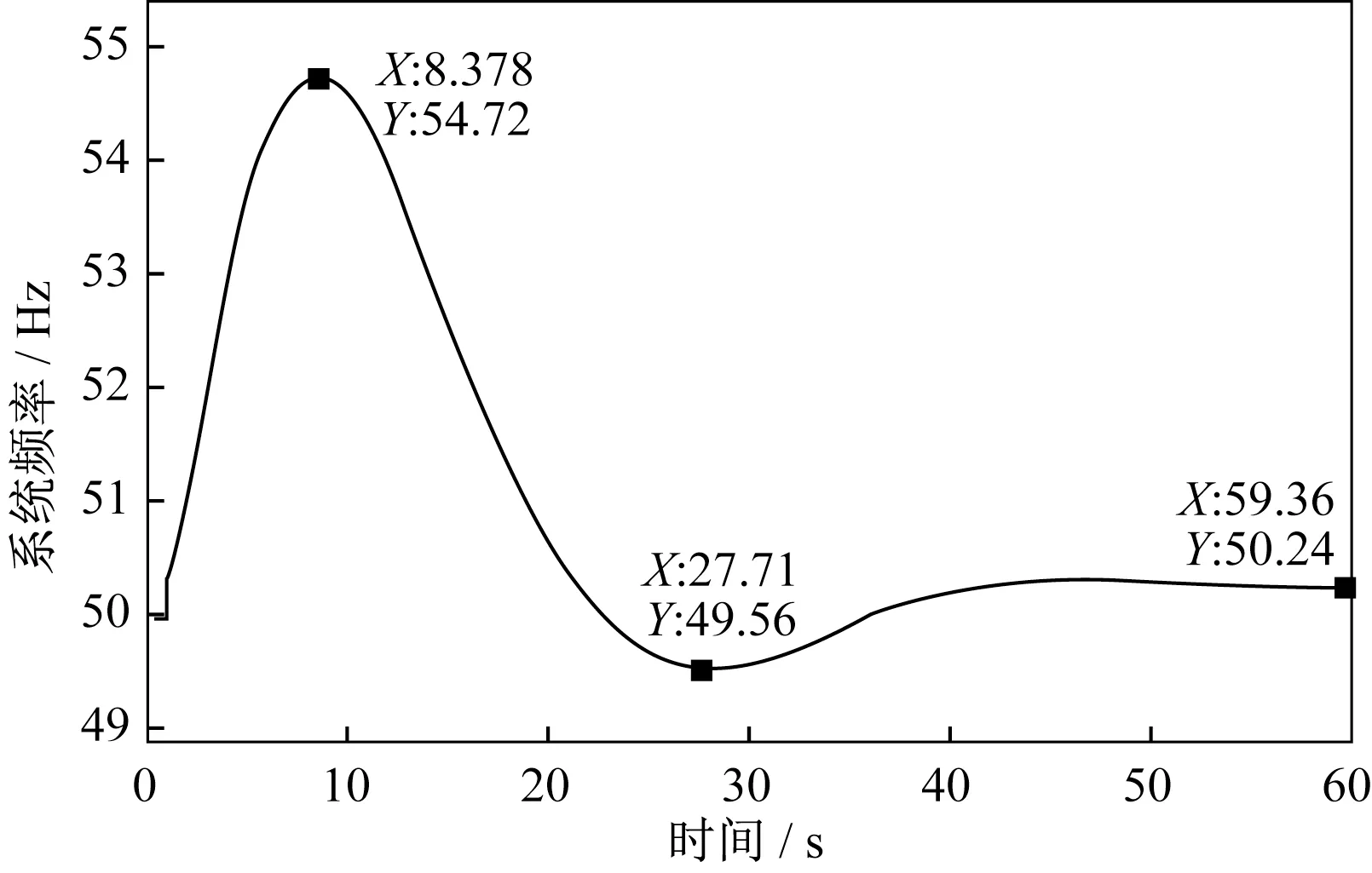
图9 场景5模式下系统频率波形图Fig.9 System frequency waveform in scenario 5
五组场景模式下峰值频率与稳定频率如表2所示。数据的对比发现,当水轮机侧电源供电距离由4 km增加到10 km的过程中,孤岛下水光配电网系统频率上升的峰值由54.72 Hz增加到62.63 Hz,稳定后的频率由50.24 Hz增加到51.06 Hz。

表2 不同供电距离下孤岛后频率值Table 2 Islanding frequency value under different power supply distance
3 结语
结合山区小水电与光伏发电运行的实际情况,本文仿真含水光配电网的运行情况,重点对孤岛初期频率特性进行研究。以场景一作为对照组,与场景二至场景五进行对比,研究发现:
1)光伏供电距离的远近对系统孤岛情况下的频率稳定性影响较弱;
2)在一定范围内,水轮机供电距离越长,孤岛后水光配电网系统频率上升峰值越高,系统越不稳定;水轮机供电距离越短,孤岛后水光配电网系统频率上升峰值越低,稳定后的系统频率越接近50 Hz。由于水轮机对频率的支撑作用,系统孤岛运行时具有较好的稳定性。
