基于未确知测度模型的防暴弹药使用安全性评估*

宋 科，马永忠

（1.武警工程大学 装备管理与保障学院，陕西 西安710086；2.武警阳泉支队参谋部，山西 阳泉045000）

防暴弹药虽然是一种非致命弹药，但在使用时安全问题较多、不确定性强。从目前研究成果来看，王佳通过对弹药性能与温湿度研究得出弹药包装技术承担着弹药的存储和防护任务并影响着弹药的使用安全[1]；崔晓萍在对某爆炸型催泪弹的使用安全可靠性试验评价时得出不同存储时间对防暴弹药的作战效果影响明显[2]；郭三学在爆震弹破片非致命效应研究中得出某型爆震弹使用时产生的较大破片在近距离对有生目标能造成致命伤害[3]。上述文献从单个因素入手对影响防暴弹药安全使用进行了深入研究，但防暴弹药的安全性还受弹药性能与状态、使用人员训练水平和使用环境等多个因素影响。因此，文章立足于防暴弹药使用的全过程，分析影响防暴弹药使用安全的因素，研究各因素所占权重，为保证防暴弹药安全使用提供理论支撑。

1 影响防暴弹药使用安全的因素

从近几年的研究成果来看，杨延海在仓储弹药安全要素研究中分析了影响弹药存储安全的因素主要在于人、设备和管理等几个方面[4]；宣兆龙在野战弹药环境安全的灰色模糊综合评判中研究得出气候、力学、电磁、战场对抗等环境因素对弹药安全性影响较大[5]；毕晓焘在闪光爆震弹预控破片设计与飞散特性研究中得出防暴弹药爆炸破片飞散角在30°～60°[6]。防暴弹药在长期储存和使用过程中，由于人的不安全行为、物的不安全状态和环境的不安全条件，均可造成弹药装备各类事故的发生，因此分析影响防暴弹药使用安全因素应从弹药性能与状态、人员及环境因素三个方面进行分析。

在防暴弹药使用中，首先要清楚所使用防暴弹药的性能与状态，比如要考虑杀伤半径及化学试剂刺激性强度、弹药生产年限、数质量及包装情况；同时要考虑使用人员的政治素养和训练情况，保管人员的业务能力等；其次要掌握温湿度、风向、海拔和可能发生的恶劣天气等自然环境因素；临时使用时还要提前计划弹药补给，考虑临时弹药库的选址和安全防卫，防止盗抢、雷击等不安全情况发生，确保整个使用过程安全可靠，为高效完成任务打下坚实基础。综合不同的影响因素，构建防暴弹药使用安全评价指标体系，如图1所示。

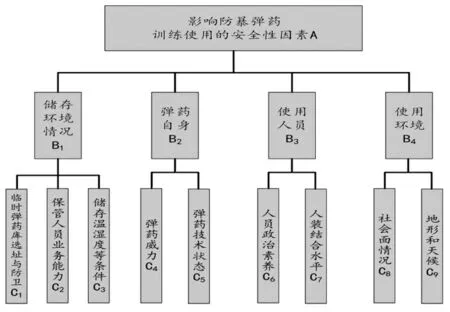
图1

2 未确知测度模型

为了有效地解决面临“不完整信息”的问题，本文引入了一种全新的方法——未确知测度模型。这一方法凭借其严谨的逻辑过程，避免了推理时可能存在的信息损失，在针对“未确知信息”的处理和数学表达研究上有着天然优势。

2.1 单指标未确知测度[7]

作为一种可能性测度，单指标未知测度是指用来衡量“程度”的测量结果，需要满足归一性、可加性以及非负有界性这三条测量准则。为了定义单指标未确知测度的具体形式，首先给出两个集合A，B，其中A={a1，a2，...an}被称为论域，ai表示在遂行任务中影响待评价防暴弹药对象使用安全性的综合评价因素指标（总计有n个），也被称作单因素评价指标；对应于每个相互独立的单因素评价指标ai又有m个评价等级，将这些评价等级记为集合B={b1，b2，...bm}。

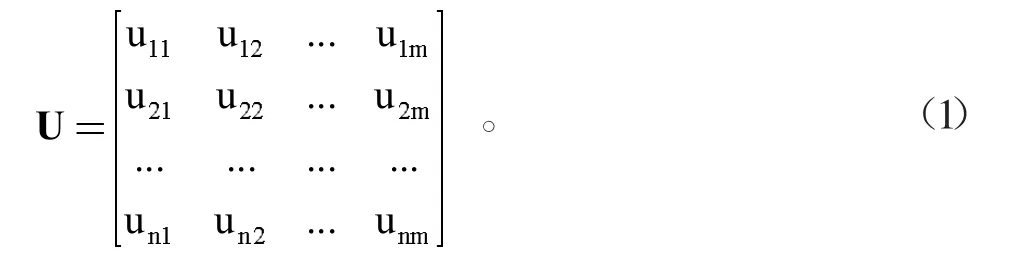
在本文的未确知测度模型中，采用专家打分法进行评估。具体方法是将单因素评价指标ai在评价等级bj上的观测值记作aij，由专家将0～100之间的分数打给每个单因素评价指标ai及其对应的评语等级bj，同时规定在所有评语等级上的单因素评价指标总得分为100分，即Σl≤i≤n，l≤j≤maij=100。在此基础上，通过归一化方法定义待评价防暴弹药在单因素评价指标ai评价等级bj上的未确知测度uij=aij/100，继而可得到待评价对象的单指标未确知测度评价矩阵。

2.2 指标权重的确定

作为一种观测值域的分布泛函，熵[8-11]常常被用作描述与观测值之间相关的不确定性，即定量地刻画不确定性或混乱度。熵（entropy）的概念最早由克劳修斯提出，主要用作热力学系统中状态的描述，具有对称性、非负性、可加性、极值性等特点。此后这一概念被拓展应用到多个不同领域当中。在统计学中，离散型随机变量的信息熵定义为假设在一个自然状态空间中存在n个不确定因素X＝（x1，x2，...xn），其中xi为真实观测到的状态。如果在这个自然状态空间中n个不确定因素发生的先验概率分布为P（X）={P（x1），P（x2），...，P（xn）}，则该状态的未确知测度的熵函数为：

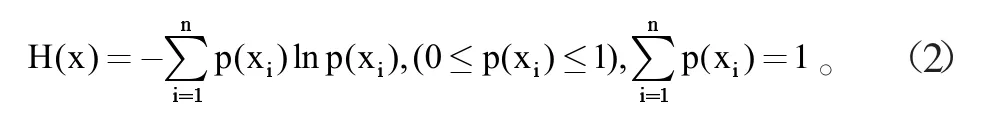
将上一节中所计算得到的未确知测度代入式（2），则可以得到在给定状态下各未确知测度的熵为：

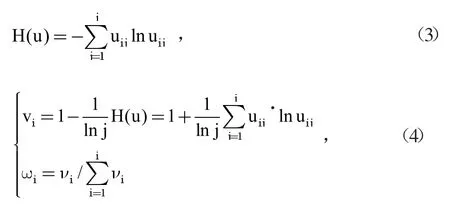
ωi即为在遂行任务中待评价防暴弹药安全性单因素评价指标ai的权重。W=[ω1，ω2，...ωn]则为相对应的权重向量。

2.3 综合评价系统

基于式（1）与式（4）给出的单指标未确知测度评价矩阵以及对应的权重向量，可以给出在遂行任务中待评价防暴弹药安全性综合测度评价向量如下：

这一向量中描述了待评价对象在m个不同的评价等级当中的不确定性程度。注意到评价等级B={b1，b2，...bm}的划分是单调降序排列的，因此可以在此基础上进行置信度识别。很明显最大测度识别准则不能够适用于这种情况，因此我们在此改用置信度识别准则。对于给定的不小于0.5的置信度 λ（通常取为0.6或0.7），可以给出置信度识别模型如下：

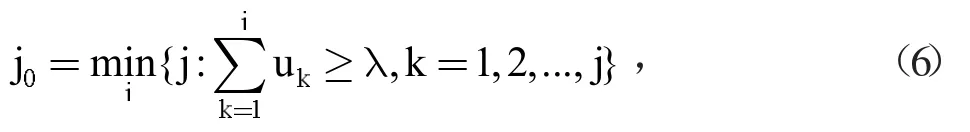
取j值直至满足公式（6），则在遂行任务中待评价的防暴弹药安全综合评价结果为第j0个评价等级uj。

3 案例分析

为验证未确知测度模型在防暴弹药使用时安全性评估的适用情况，文章以某次训练为例对模型进行验证。

案例：某部计划在野外组织防暴弹实弹训练，参加训练的人员军政素质良好，但缺少防暴弹使用的经验；野外条件较为恶劣，当地气温适宜，但可能会出现大风和雷雨的天气情况；此次训练要对多个弹种进行实弹实投训练，本批弹药保存完好、技术性能正常。为合理管控安全风险，计划在开始之前对此次训练的安全性进行评估，确定安全风险等级，为下步训练工作打下基础。

下面利用未确知测度模型对此次驻训任务的防暴弹药安全性评估，首先采用专家打分法，将各影响因素分为很安全、较安全、一般安全、不安全、很不安全5个等级进行评定，确定单指标测度评价矩阵，打分结果统计如表1：

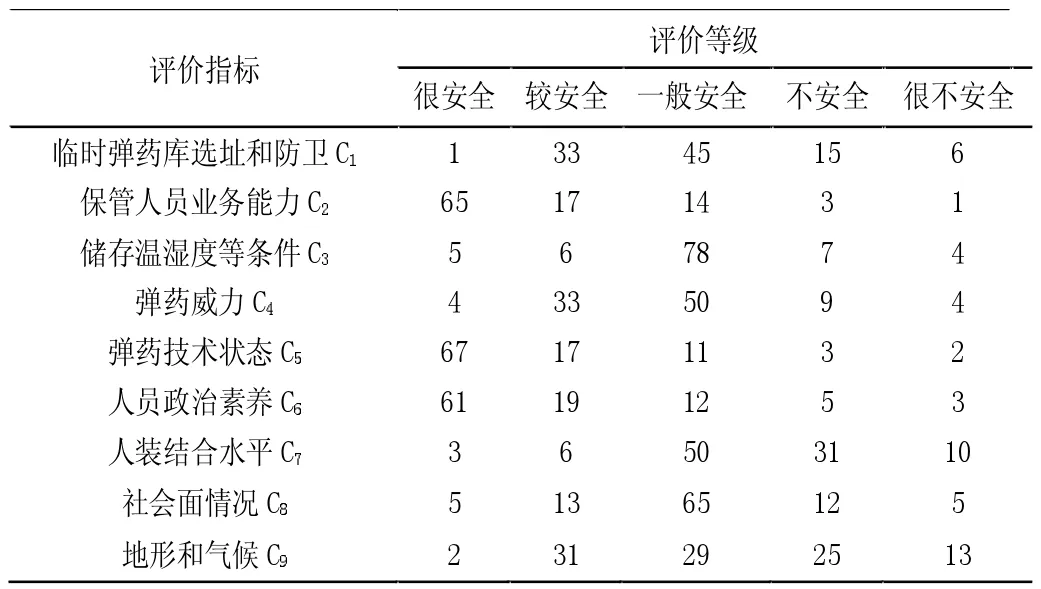
表1 专家打分结果统计表

由以上打分结果，得到单指标未确知测度评价矩阵：

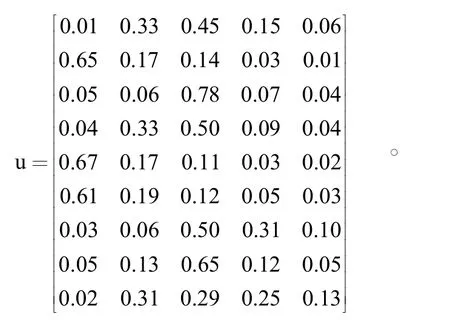
根据公式（4）计算出影响因素的指标权重可得：ω=（0.1153，0.1065，0.0992，0.1138，0.1060，0.1113，0.1148，0.1102，0.1229）。

根据公式（5）求得最终的评判结果：

μ=（0.2302，0.1981，0.3908，0.1260，0.0549）。

取置信度λ=0.7，根据置信度识别准则及公式（6）判定此次防暴弹药使用的安全评价等级为第3等级，即“一般安全”。

4 结论

文章通过建立基于熵权的未确知测度的防暴弹药使用安全性模型，并结合实例对未确知测度模型在防暴弹药使用的安全性综合评价中的应用进行了初步探讨，实现了对影响安全因素的综合评价。

（1）基于未确知测度理论的防暴弹药使用的安全性综合评价模型的运用表明，其在各评价指标权重和识别准则的确定上，分别采用了信息熵和置信度识别准则，避免了模糊数学、层次分析法以及灰色关联理论等评判法在这些方面的不足，使评价结果更具客观性。

（2）通过基于未确知测度理论的防暴弹药使用的安全性综合评价模型的研究及其实际应用表明，未确知测度模型能够很好地对防暴弹药使用安全性进行综合评价，其评价指标可根据实际情况灵活选取，评价模型计算简单，其对安全性的评价结果为组织训练人员，提前根据实际情况，适时调整方案，为确保防暴弹药使用安全提供决策依据。

（3）未确知方法注意了评价空间的有序性，给出了比较合理的置信度识别准则和排序的评分准则，而这正是模糊数学、层次分析法以及灰色关联法评判所不具有的优点。