隔声量的阻抗管法和混响室法仿真计算对比

2021-08-21漆琼芳李英伟

噪声与振动控制 2021年4期

张苗，漆琼芳，李英伟

（1.武汉第二船舶设计研究所，武汉430000；2.渤海造船厂集团有限公司，辽宁葫芦岛125004）

在船舶、轨道交通、建筑等行业经常出现噪声污染，因此所使用的壁板一般具有一定的隔声性能，隔声量是隔声构件的一项重要指标，是指材料一侧的入射与另一侧的透射的声功率级差，目前对隔声量的估算主要采用等效质量法和质量定律等，隔声量测试可采用驻波管和混响室法[1–2]。

目前，刘冬冰[3]根据垂直入射阻抗管传递函数法、四传声器法编写了吸声系数和隔声量计算程序，并将隔声量理论值和数值仿真结果进行对比，验证了所设计的斜入射隔声阻抗管的设计可行性。董明磊[4]分析混响室隔声量的测试原理，并推导了三传声器法、四传声器法及改变边界的四传声器法的隔声量计算公式，设计了隔声量数据处理仪器，计算仿真值与仪器测量值吻合较好。赵阳[5]基于四传声器阻抗法原理，引入声源反射系数和吸声末端的反射系数，推导了考虑反射修正的试件隔声量公式，采用北京声望阻抗管进行测试得到4个传声器通道的复声压，根据提出的修正公式对传递损失进行修正，将试件解析解与修正值进行对比，验证了所提出的隔声量修正公式的准确性。石嘉欣、杨德庆等[6]采用有限元法模拟驻波管，并与混响室模型和瑞利李兹法进行比较，确定了驻波管模型的边界条件。刘杰等和张树峰[7–8]采用FEM 法的AML 技术模拟无反射边界，并定义结构-内声场-外声场的耦合面，对隔声罩进行声-振耦合计算。

本文分别基于驻波管和混响室法建立了试件隔声量仿真模型，通过建立试件结构域与周围空气域的声-振耦合模型，施加无反射边界模拟消声室，采用随机声场模拟无指向性声源等方法，得到声-振耦合计算的测点声压值，并根据后处理公式编程得到试件隔声量，探讨了试件边界条件、夹层、声波入射形式等参数对隔声量的影响。

1 声学模型理论方法

1.1 声学有限元

声学有限元的原理是将求解域划分成一系列单元，单元之间由节点相连，引入插值函数用以描述单元变量，依据变分及加权余量等建立声学有限元方程，根据声压、阻抗、质点振速等边界条件求取节点变量，从而得到节点处变量的近似数值解。

理想流体介质中声压的波动方程为

式（1）解的形式为p2(x,t)=f(ωt-kx)+g(ωt+kx)，其中：x是位移，t是时间，ω是声波角频率，波数k=2πf/c，f是频率(Hz)，c是声速(m/s)，管中声速c=343.2，T为空气温度(K)，p是管道内声压(Pa)。式(1)中，c0是声速，p是声压。

声学有限元中采用插值函数：

其中：{N}是节点声压列向量，{p}是形函数列向量。

根据格林函数将式(1)转化为

其中：∂n是结构外法向，边界表面S=Sr +Sv +Sz，Sr、Sv、Sz分别是刚性壁面表面、法向质点振速表面和法向声阻抗表面，一般定义3种声学边界条件。

刚性壁面边界条件为

法向质点振速un的边界条件为

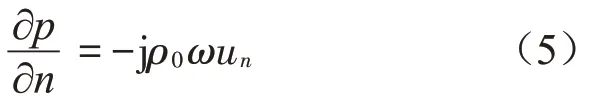
法向声阻抗z的边界条件为

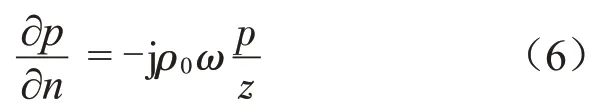
根据声学边界条件，得到等式：

1.2 四传声器的阻抗管法

隔声量测试所用阻抗管如图1 所示，发声管内的扬声器近似发出平面波声源，假设发声室的正向波为PA，反向波为PB，接受管内的正向波为PC，反向波为PD，传声器1#、2#、3#、4#与试件近端面的距离分别为x1、x2、x3、x4，传声器测点声压分别为P1、P2、P3、P4，接受管端部有吸声的声学末端。

图1 隔声量测试用阻抗管

根据四传声器法，发声管和接收管内传声器1#、2#、3#、4#的复声压分别为

其中：波数k=2πf/c，f是计算频率（Hz），c=343.2是管中声波的速度（m/s），T是空气温度（K）。

试件的透射系数τp为

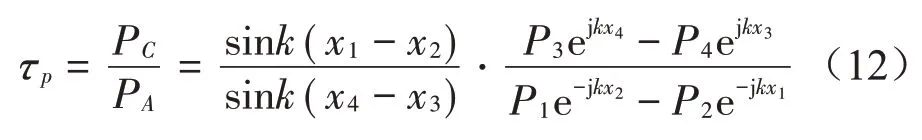
试件的传递损失TL为

四传声器法忽略声波多次反射，只考虑声学末端的一次反射，因此声学末端的吸声越佳，测量结果越精确。

1.3 混响室法

隔声量测试所用的混响室一般如图2 所示，在发声室（混响室）布置无指向性声源用于发射声波，发声室的壁面反射较高，可将发声室的声场视作扩散声场。在接收室（消声室）四周布置吸声尖劈等，可将接收室内的声场视作自由声场。试件安装在发声室和接受室中间墙面的孔洞上，可认为发声室的声波无规则入射到试件上。

图2 隔声量测试用混响室

试件的入射声功率Win为

其中：为混响室声压均方值，S为试件的表面积，ρ0是空气密度，c0是声音在空气中速度，S是试件面积。

因此试件的入射功率Win为

其中：pa为入射声腔的声压幅值。

透射声功率Wt与总声强I和试件表面积满足：

传递损失TL为

仿真时根据式（15）计算出入射声功率，提取试件与接受室的耦合声功率即透射声功率，通过式（17）得到试件的传递损失，称之为隔声构件的隔声量。

1.4 隔声量曲线质量定律

假如声波以θ角斜入射，根据质量定律，单层板隔声量公式[2]为

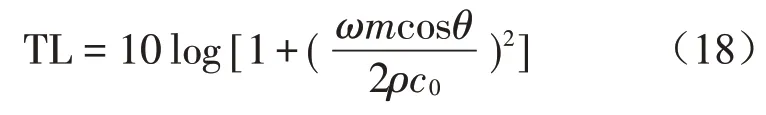
其中：m是单位面积质量（kg/m2），ω是圆频率，f是频率（Hz），ρ是空气密度（kg/m3）；c0是声速（m/s）。

若声波垂直试件入射，传递损失TL1为

若声波随机入射，传递损失TL2为

在测试或仿真时板隔声量曲线可能出现V型低谷，这是由于板弯曲波波长等于入射波波长在板方向的投影时，两波产生共振造成隔声量下降，该现象称为吻合效应，最低吻合频率称为临界频率[2]。比共振频率低的频段称为刚度控制区，比共振区高的频段进入质量控制区，共振频率估算公式如下：

其中：c0是声速，θ是声波入射角，E是材料弹性模量，μ是材料泊松比，h是板厚。

2 建立声学模型

2.1 声学计算模型的建立

2.1.1 阻抗管模拟法

如图3 所示，阻抗管内径为100 mm，发声管长480 mm，接收管长580 mm。建立试件的结构有限元以及阻抗管内空气域的声学有限元，单元尺寸为10 mm，为保证每个单元尺寸至少大于等于6个声波长，计算频率范围取为5 Hz～4 000 Hz。在发声管初始端施加速度载荷，模拟扬声器的平面波声源，声波垂直入射到试件上，在接收管端部施加无反射边界条件，模拟声学末端，根据四传感器法的距离关系设置传声器测点，采用Virtual. Lab Acoustic 软件进行直接声-振耦合计算，提取传声器测点的复声压，再根据四传声器法公式即式（8）至式（13）进行后处理，采用MATLAB编程计算试件在垂直入射波作用下的传递损失。

2.1.2 混响室模拟法

如图4 所示，采用混响室模拟法时的试件尺寸与阻抗管模拟法一致，在试件左右两边建立空气域有限元模型，模拟混响室里的发声室和接受室，基于试件结构域与两侧空气域分别建立声-振耦合面，在接受室非声-振耦合面设置声波向外辐射而无反射边界，模拟半消声室的自由场。在试件发声室一侧设置12 个随机平面波声源，用于模拟混响声源，声波非垂直无规则入射到试件上，也可设置平面波声源，模拟声波垂直入射在试件上。

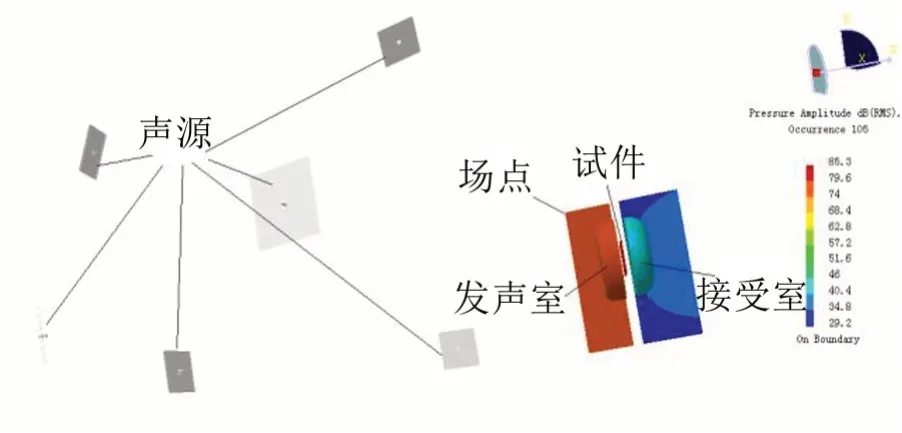
图4 隔声量计算的混响室模拟法

采用Virtual. Lab Acoustic 进行直接声-振耦合计算及随机声场计算，根据12个平面波工况的耦合响应合成随机计算的响应，分别提取试件与发声室耦合面的声功率和试件与接收室耦合面的声功率，根据式（14）～式（17）计算试件的在无规则入射波作用下的传递损失。

2.1.3 声学模型的有效性验证

对比声波在无限介质中垂直入射中间层的理论隔声量公式计算结果、文献测试值[3]与本文阻抗管法模拟的结果。其中，本文阻抗管模拟法所采用的试件为铝板，弹性模量为70 GPa，泊松比为0.3，密度为2 700 kg/m3，厚度为10 mm，对试件结构不施加约束，网格尺寸为10 mm，在发绳室一侧施加1 m/s 速度激励模拟平面波声源的垂直入射。文献[3]中采用自主设计的阻抗管，管壁厚10 mm，测试13 种试件的隔声量，所选择试件6 为2 mm 铝板，与本文阻抗管试件一致。得到隔声对比曲线如图5所示。

图5 隔声量仿真的有效性验证

在5 Hz～2 kHz范围内，阻抗管模拟法的结果和解析解接近。在300 Hz～4 kHz 范围内，仿真值、解析解和实验值较为接近。测试值在1 600 Hz 有低谷，这可能与测试时试件的安装状态有关，不同边界条件影响了试件安装模态，造成在某些固有频率下产生隔声低谷。3种方法所得的隔声量曲线在趋势上较接近，说明阻抗管四传声器模拟法是仿真计算隔声量的一种有效方法，验证了根据式（8）至式（13）编制的隔声量计算程序的准确性。仿真计算结果与测试值存在差别，这是因为试件并非理论上的无限大障板，试件的边界条件、刚度、阻尼、吻合效应等会影响隔声量测试结果。

对2.1.2 节中所述阻抗管内试件施加刚性固定约束，将平面波声源入射到试件上。对2.1.3节所述混响室中的试件采用刚性固定约束，采用直径2 500 mm 的半球形模拟发声室和接受室，发声室一侧采用出至于试件的平面波模拟，发声室和接受室的单元尺寸10 mm，在发声室和接受室外侧设置快速吸收AML模拟无反射边界，使用混响室法仿真模型的混响室大小、网格密度、AML 均满足25 00 Hz 计算频率上限。在1/3倍频程10 Hz～2 500 Hz范围内的隔声量曲线如图6所示，曲线变化趋势较为一致。

图6 混响室法和阻抗管法所得隔声量对比

3 模型参数对结果影响分析

3.1 试件边界条件对隔声量的影响

以阻抗管模型为例，铝板直径为100 mm，厚为2 mm，设置铝板3 种类型的边界条件，分别为自由、简支和刚性固定，隔声量计算结果如图7所示，在计算频率5 Hz～4 kHz范围内，试件在自由状态下时其计算结果与文献测试值[3]较为接近。当频率增加至大于2 500 Hz 时，试件在简支和刚性固定边界下的隔声量曲线较为接近。当试件刚性固定时，隔声量曲线有明显的峰值和低谷，曲线呈现震荡现象。当试件处于自由边界状态时，隔声量曲线较平缓无明显震荡现象。总结以上现象可知试件边界约束越强，隔声量曲线上下震荡越明显，在低频阶段，试件边界约束越强，隔声量偏大，这是因为在低频阶段，隔声量处于刚度控制区，仿真时若对试件施加刚性约束则试件刚度增加，在低频刚度控制区域刚度越大则隔声量越大。在自由状态下仿真时，试件尺寸较大时，可认为其尺寸近似于半无限尺寸，这种情况下与质量定律下的声传播特性较为一致。实际工程应用中，试件几乎不能达到完全刚性、完全简支或完全自由状态，因此进行隔声量仿真计算时，建议采用自由边界条件，得到的曲线较为平缓且呈现出质量控制区特性，在全频段与测试值较为接近。随着频率的继续上升，试件进入质量控制区，隔声量主要与试件面密度有关，所以3 种边界条件下仿真结果较接近。试件隔声低谷一般出现在结构的共振频率附近，试件模态与约束边界条件有关，试件所受约束为简支时，1 kHz 左右出现隔声低谷，试件所受约束为刚性支撑时，2 kHz 左右出现隔声低谷，试件边界约束越强，试件刚度越大，隔声低谷越向高频移动。

图7 不同边界条件对隔声量的影响

3.2 夹层对试件隔声量的影响

根据混响室模型，取公路两侧声屏障常用的PMMA 板为研究对象。假设试件尺寸为0.9 m×1.2 m，弹性模量为53.5 GPa，泊松比为0.35，密度为1 180 kg/m3，试件分别为：试件1（10 mm PMMA板）、试件2（5 mm PMMA 板+60 mm 空气层+5 mm PMMA 板）、试件3（5 mm PMMA 板+100 mm 空气层+5 mm PMMA板）。网格尺寸小于最大计算频率的1/6，网格密度能满足最大计算频率为2 000 Hz的要求，但由于使用了大范围的自动匹配边界层（AML）模拟无反射边界，网格密度能满足最大计算频率为510 Hz 的要求，最终取计算频率为5 Hz～510 Hz，得到隔声量曲线如图8 所示。可知当使用随机声源和空气域时，采用声-振计算所得的曲线震荡比较大，并非呈现出文献[2]中光滑的曲线，随着夹心层厚度的增加，隔声低谷有向低频移动的趋势。

图8 夹层厚度对试件隔声量影响

3.3 无规则入射与垂直入射对隔声量的影响

采用4.2节中所述的试件1为研究对象，设置自由边界，分别采用平面波入射和混响声源入射到试件上。

（1）无规则入射：发声室内混响声源无规则入射到试件上，设置试件结构网格与空气域的耦合面，采用12 个随机平面波声源模拟12 面的无指向性声源。

（2）垂直入射：发声室内平面波垂直入射到试件上，设置试件结构域和空气域的声-振动耦合，采用一个沿试件法向的平面波模拟垂直入射。

根据两种入射方式计算所得的隔声量如图8所示。当声源为平面波垂直入射时或者随机无规则入射时，隔声量曲线如图9 所示。在200 Hz 以上垂直入射相较无规则入射计算所得的隔声量偏大，但在50 Hz～200 Hz范围内偏小，与式（20）所反映的一般规律有所不同，有可能与采用声学有限元计算时发生的曲线震荡有关。