基于集成学习的改进灰色瓦斯浓度序列预测*
2021-08-20赖祥威夏云霓郑万波崔俊飞吴燕清史耀轩
赖祥威,夏云霓,郑万波,崔俊飞,吴燕清,史耀轩
(1.昆明理工大学 理学院,云南 昆明 650500;2.昆明理工大学 数据科学研究中心,云南 昆明 650500;3.重庆大学 计算机学院,重庆 400030; 4.中煤科工集团重庆研究院有限公司,重庆 400037;5.瓦斯灾害监控与应急技术国家重点实验室,重庆 400037;6.重庆大学 资源及安全学院,重庆 400030)
0 引言
瓦斯浓度预测是煤矿安全生产重要环节。国内学者针对瓦斯预测开展研究:杨丽等[1]基于多元分布滞后模型(MDL)提出多变量瓦斯浓度时间序列预测模型;胡坤等[2]为准确预测瓦斯涌出量,建立回采工作面瓦斯涌出量优化预测模型;李冬等[3]为提高瓦斯突出危险区域预测精度,建立瓦斯突出危险区域综合预测方法;李成武等[4]为预测矿区突出能量,通过引入煤体当量半径,推导突出能量预测模型;张友谊等[5]通过研究灰色关联模型输出端与输入端,提出煤与瓦斯突出多指标耦合预测模型。此外,国内部分学者基于神经网络、随机森林等时间序列进行预测研究[6-8],但均需基于大量数据,针对信息匮乏的时间序列研究,灰色理论在能源消费、电网安全运作能力等众多领域得到充分运用[9-15],但在煤矿瓦斯预测领域研究较少。现有煤矿瓦斯浓度预测方法为传统灰色预测模型,但传统灰色预测模型灰色作用量为常量,不随时间发生变化。因此,本文通过对传统灰色模型进行优化,得到随时间改变的幂指数灰色作用量,并提出基于集成学习的幂指数型灰色瓦斯浓度预测模型,研究结果可有效提瓦斯浓度预测精度。
1 预测算法设计流程与评价分析
灰色预测在解决不确定性问题,尤其对于小样本时间序列问题具有一定优势。通过将历史数据序列累加得到生成序列,建立灰色预测模型,实现对未来发展趋势预测。
1.1 传统灰色预测模型
传统灰色预测模型建立主要包括以下5个步骤:
1)设原始瓦斯浓度序列如式(1)所示:
(1)
经1次累加生成瓦斯浓度序列,如式(2)所示:
(2)
经1次累减生成瓦斯浓度序列,如式(3)所示:
(3)

2)X(1)紧邻均值生成序列如式(4)所示:
(4)
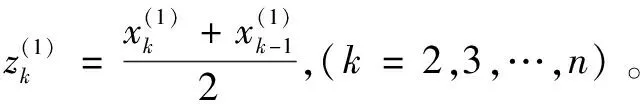
3)传统灰色预测模型如式(5)所示:
(5)
式中:k=2,3,…,n。
利用1阶单微分方程拟合,得到传统灰色预测模型白化方程,如式(6)所示:
(6)
式中:a为发展系数;b为灰色作用量。
4)在传统灰色预测模型中,利用最小二乘法进行参数估计,向量u,Y,B分别如式(7)~(9)所示:
u=[a,b]T=(BTB)-1BTY
(7)
(8)
(9)
基于式(7)~(9)求解传统灰色模型白化方程,得到瓦斯浓度响应序列,如式(10)所示:
(10)

5)利用1次累减生成瓦斯浓度序列,得到瓦斯浓度预测值序列,如式(11)所示:
(11)
1.2 优化后幂指数型灰色预测模型
实际问题中,灰色作用量随时间变化而变化。因此,本文通过对灰色作用量进行优化,得到幂指数型灰色作用量,建立改进后灰色预测模型。主要包括以下5个步骤:
1)将传统灰色预测模型对应白化模型静态灰色作用量替换为幂指数型灰色作用量,即将b替换为beαk+c(其中α为参数),得到改进后灰色预测模型白化模型,如式(12)所示:
(12)
改进后灰色预测模型如式(13)所示:
(13)
式中:c为参数。
2)设向量Y,B如式(14)~(15)所示:
(14)
(15)
式中:β=a-1(eα-1)。
参数估计向量u如式(16)所示:
向量u=[a,b,c]T=(BTB)-1BTY
(16)
3)假设任意函数μ(k)满足式(17):
μ′(k)=aμ(k)
(17)
通过求解可得式(18):
μ(k)=heak
(18)
式中:h为常数。
4)将式(12)两边同乘μ(k)并积分,如式(19)~(21)所示:
(19)
(20)
(21)
式中:C为常数。
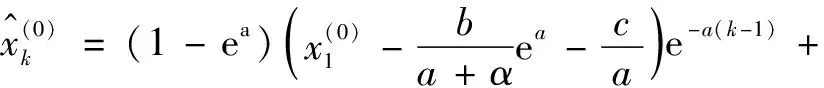
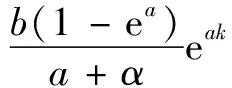
(22)
式中:k=1,2,…,n;a,b为常数。
1.3 基于集成学习的幂指数型灰色预测模型
集成学习通过将多种不同模型按照权重加权组合得到新预测模型。本文采用标准差法得到瓦斯浓度组合预测模型权重,进行瓦斯浓度预测。组合预测模型构造流程如图1所示。
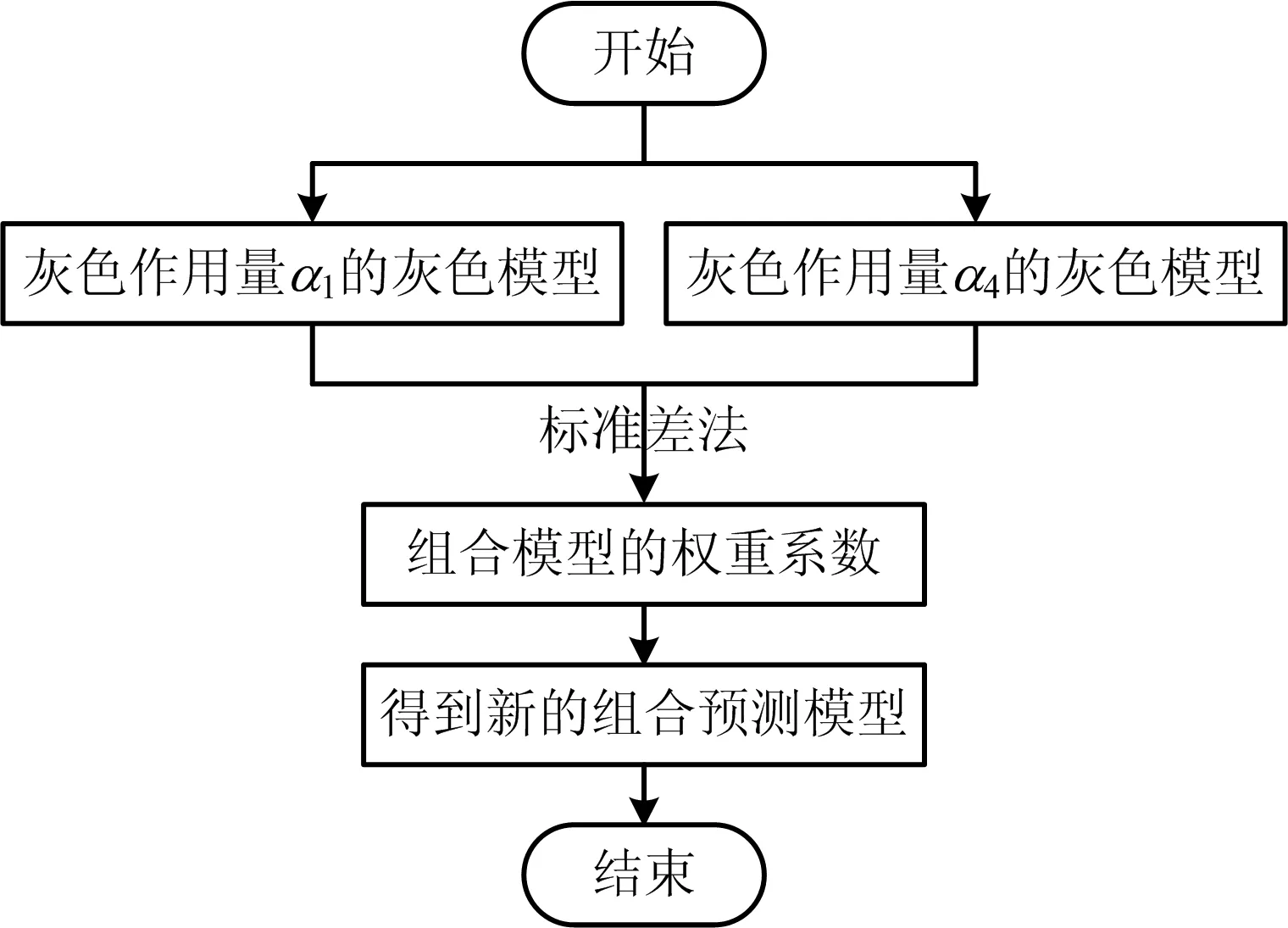
图1 组合预测模型构造流程
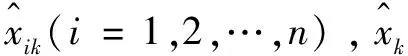
(23)
同时,需满足预测误差平方达到最小准则,如式(24)~(25)所示:
(24)
(25)
式中:xk为k时刻瓦斯浓度实际值,%。
1.4 模型评价指标
本文采用均方根差(RMSE)与平均绝对误差(MAE)对不同算法预测精度进行科学评价。均方根差与平均绝对误差如式(26)~(27)所示:
(26)
(27)
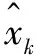
2 瓦斯浓度预测仿真实验
2.1 实验数据
本文以吉林八连城矿井为研究背景,基于八连城瓦斯监控数据,采用不同算法进行预测,并对实验结果进行讨论分析。实验数据来源于八连城煤矿瓦斯灾害风险管控平台2021年1月1日至2021年2月1日以及2021年2月1日至2021年2月4日长期与短期瓦斯监控数据。八连城煤矿瓦斯灾害风险管控平台如图2所示。

图2 八连城煤矿瓦斯灾害风险管控平台
瓦斯浓度监控传感器数据24 h不间断采集(极少部分数据缺失),瓦斯浓度序列数据时间间隔1 h。选取其中2个矿井工作面(南11902上顺工作面、北12005上顺工作面)监测数据作为实验数据。以数据集前75%数据作为训练集,剩余25%数据作为测试集。2个矿井工作面瓦斯浓度传感器采集数据周期见表1。

表1 2个矿井工作面瓦斯浓度传感器采集数据周期
2.2 实验结果
采用瓦斯浓度序列传统灰色预测模型,幂指数型灰色预测模型及基于集成学习的指数型灰色预测模型,对矿区南11902上顺工作面、北12005上顺工作面数据集瓦斯浓度数据进行预测,并对预测误差进行分析。
1)南11902上顺工作面不同预测模型预测值与误差分析
不同模型训练集与测试集绝对误差如图3所示,不同模型下预测值误差分析见表2。由表2可知,相较于瓦斯浓度传统灰色模型,幂指数型模型与集成学习模型平均绝对误差及均方根差均有所降低;在训练集短期预测中,基于集成学习的指数型预测模型误差相对较小,较传统灰色预测模型平均绝对误差和均方根差分别下降1.27%,1.26%;长期预测中,基于集成学习的指数型预测模型较传统灰色预测模型平均绝对误差和均方根差分别下降1.76%,2.25%。
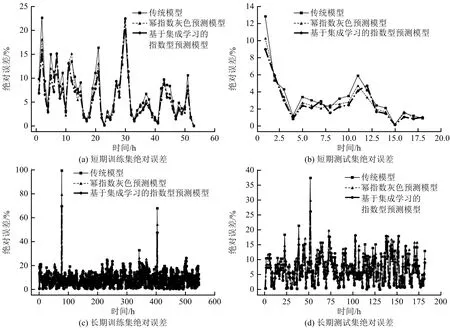
图3 南11902上顺工作面不同模型绝对误差
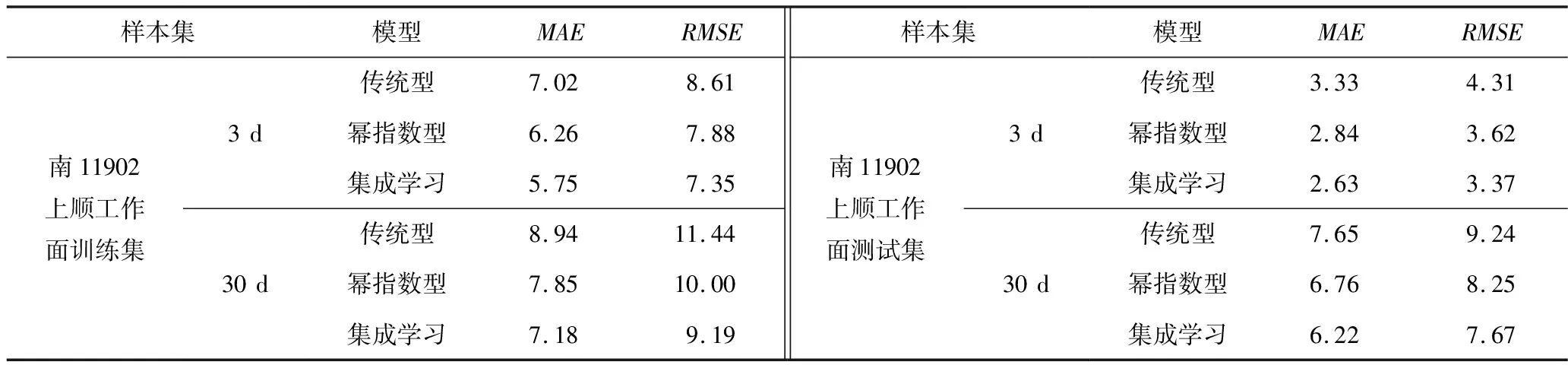
表2 南11902上顺工作面不同模型下预测值误差
在测试集短期预测中,基于集成学习的指数型预测模型误差相对最小,较传统灰色预测模型平均绝对误差和均方根差分别下降0.7%,0.94%;长期预测中,平均绝对误差和均方根差分别下降1.43%,1.57%。
2)北12005上顺工作面不同模型预测值及误差分析
不同模型训练集绝对误差与测试集绝对误差如图4所示,以不同模型下预测误差分析见表3。由表3可知,相较于瓦斯浓度传统灰色模型,幂指数型模型与集成学习模型平均绝对误差和均方根差均有所降低。在训练集短期预测中,集成学习模型误差相对最小,较传统型平均绝对误差和均方根差分别下降0.51%,0.45%;长期预测中,集成学习模型较传统型平均绝对误差和均方根差分别下降0.95%,1.99%。
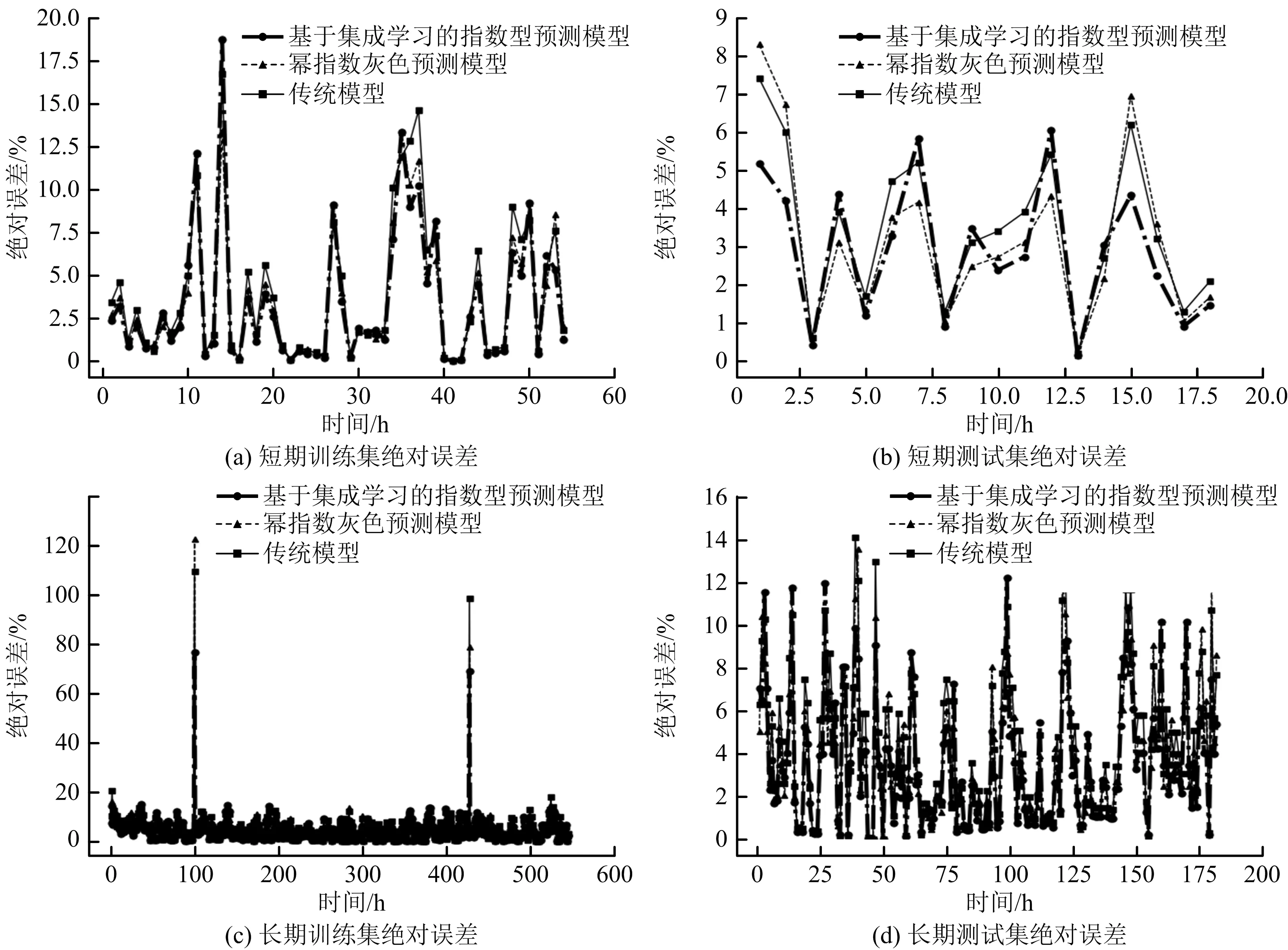
图4 北12005上顺工作面不同模型的绝对误差
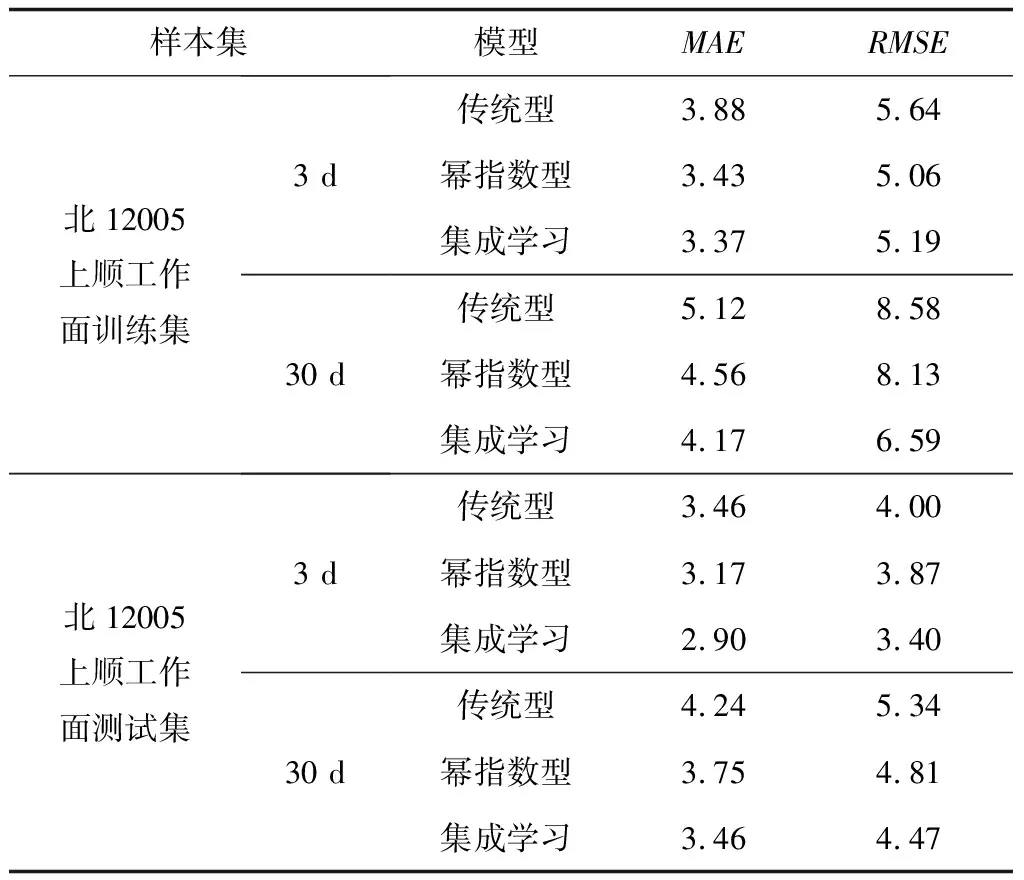
表3 北12005上顺工作面不同模型下预测误差分析
在测试集短期预测中,集成学习模型误差相对最小,较传统型平均绝对误差和均方根差分别下降0.56%,0.6%;长期(30 d)预测中,平均绝对误差和均方根差分别下降0.78%,0.87%。
综上,本文提出的基于集成学习的改进灰色瓦斯预测模型相较于传统灰色模型预测值误差更小,预测精度更高。
3 结论
1)基于集成学习的改进灰色瓦斯预测算法有效降低瓦斯浓度预测值与实际值绝对误差及均方根误差,瓦斯浓度序列均方根差最大降低2.25%,尤其针对瓦斯浓度时间序列为近似线性情况时,预测效果较好。在算法设计方面,考虑瓦斯浓度序列混沌特性,对混沌特性数据具有普适性。
2)基于集成学习改进灰色瓦斯浓度预测算法预测精度方面仍有较大上升空间。研究结果为智慧煤矿瓦斯预警提供借鉴。
