基于Python 的RSA 密码算法的设计与实现
2021-08-20白永祥陈逸怀
白永祥,何 林,陈逸怀
(1.天津职业技术师范大学自动化与电气工程学院,天津 300222;2.天津市信息传感与智能控制重点实验室,天津 300222;3.渭南职业技术学院,陕西 渭南 714000)
现代密码学体系加密算法一般分为两种:对称加密算法和非对称加密算法(亦称公钥加密算法)。所谓对称加密就是通信双方加密和解密消息时使用相同的密钥,对称密码算法的优点是加解密运算速度较快,适用于处理大批量消息处理,缺点是很难解决密钥分发的安全性和数字签名等问题。在非对称加密算法中,发送方和接收方使用不同的密钥,发送方使用接收方的公钥对明文进行加密,接收方使用自己的私钥对密文进行解密,从而获得明文内容,因公钥密码算法运算速度较慢,所以适用于处理密钥分发和数字签名等问题,一般在实际应用中,往往会将两者结合起来使用,即混合密码算法,使用非对称加密算法对密钥进行加密,对称加密算法加密内容较多的明文。
RSA 密码体制是目前较流行的一种公钥密码算法。1977 年由Rivest、Shamir、和Adleman 3 位专家提出并于1978 年首次发表的算法,人们习惯称其为RSA 密码算法[1]。RSA 算法自诞生之日起就受到广泛使用,早期的RSA 算法采用C、C++或者JAVA 实现,实现起来比较繁琐。近来年,随着Python 语言的盛行,尤其是大量开发软件包的出现,使得Python 语言应用领域不断扩大。Python 是上世纪80 年代末由Guido van Rossum 创建的,它是一种解释性的高级通用编程语言,具有动态类型系统和自动内存管理功能,并支持多种编程范例,包括面向对象、命令式、函数式和过程式,拥有一个大型的标准库。目前,Python 3.X 是主流版本,PyCrypto 是Python 下的一个密码软件包,但已经超过3 年无人维护,因此Github上的开发者们呼吁不要再使用PyCrypto,而应该使用PyCryptodome 代 替PyCrypto。PyCryptodome 是 一个包含低级密码原语的自包含包,对于要使用Python 加密库的新项目,建议开发者使用PyCryptodome 或者Cryptography。该文正是基于此软件包,针对RSA 密码体制进行了设计和实现。
1 公钥密码算法理论
公钥密码学的提出是为了解决对称密码学中密钥分配和数字签名两个难题。1976 年Diffe 和Hellman 首次公开提出了公钥密码学的概念[2],并设计了在不安全公共网络上进行安全传输密钥的协议问题。公钥密码学系统的安全性是基于单向陷门函数的安全性,所谓单向陷门函数就是正向计算函数值很容易,在缺少附加信息时计算函数的逆是不可行的,一般满足下列条件[3]:
1)若k和X已知,则可计算Y=fk(X);
2)若k和Y已知,则可计算X=fk(Y);
3)若Y已知,但k未知,则计算出不可行。
1.1 公钥密码体系的实现过程
从集合论角度看,一个公钥密码系统可以定义为一个九元组集合:

1)M为明文集合,或称作明文空间;
2)C为密文集合,或称作密文空间;
3)K为密钥集合,或称作密钥空间;
4)m∈M,是明文集合的一个子集;
5)X∈C,是密文集合的一个子集;
6)e为公钥,d为私钥,(e,d)∈K,且e≠d;
7)E为加密函数,D为解密函数;
由于m∈M,X∈C,使用公钥ek,加密如下:

8)D为解密函数,则:
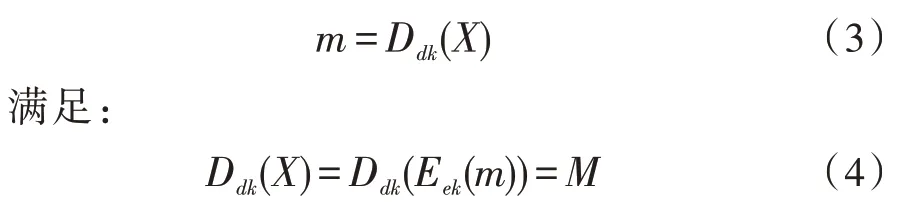
公钥密码系统工作原理如图1 所示[4]。
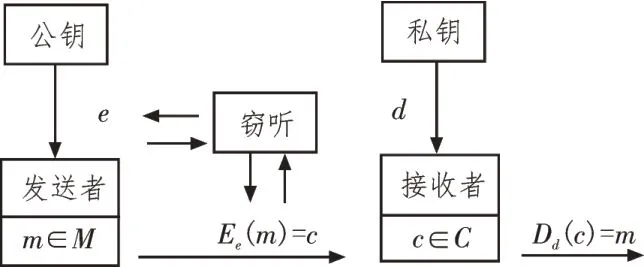
图1 公钥密码系统工作原理
1.2 公钥密码体制的应用
1)加密与解密
公钥密码系统使用一对配对的密钥实施加密和解密,由于公钥密码系统运算量大,加密和解密速度慢,使用混合加密方法,即使用对称密码算法对消息进行加密和解密,使用公钥密码算法对会话密钥进行分发。
2)数字签名
当在法律文件、合同书或私人信件上签名时,是通过手写签名来证明自己的身份。有时为了防止犯罪分子伪造签名,还需要一些验证程序,例如,销售人员通过与信用卡本身的签名进行比较来验证信用卡上的签名。在这里可以看到的是两个阶段的签名和验证过程,数字签名也是如此,它是通过网络进行加密的一种电子签名[5]。
通常数字签名方案必须满足两个安全标准:如果Alice 用Sigk(m)来签署一条消息m,那么接收方检索这对(m,Sigk(m))在计算上一定是不可行的;其次,如果Bob 从Alice 那里收到Sigk(m)=c,那 么Bob 必须能够使用Verk(c)来验证这是Alice 的签名,称为可信属性[6]。数字签名方案还需要满足另外两个属性:第一,消息被传送后,Bob 和Darth都不能改变m,称为不可改变属性;第二,Bob 必须能够立即检测到m是否被重新发送,称为不可重用性[7]。
2 RSA密码算法理论
RSA 密码体制属于分组密码,是目前最流行、应用最广泛的公钥密码系统。假设Bob 向Alice 发送消息,RSA 公钥密码系统工作流程如图2 所示[4]。

图2 RSA公钥密码算法工作流程
RSA 密码算法可以假设为一个八元组[8-9]:{M,C,K,e,d,N,E,D};1)M为明文空间;2)C为密文空间;3)K为密钥空间;4)e为公钥,d为私钥;5)E为加密函数;6)D为解密函数;7)N为p和q两个大素数之积,且p、q位数不小于100,{(e,N),(d,N)}∈K且e≠d,同时满足ed≡1(modφ(N)),φ(N)=(p-1)(q-1)。
2.1 RSA密钥对生成
1)Bob 随机生成两个大小相当的大素数p和q,且p≠q;
2)计算n=pq,φ(n)=(p-1)(q-1),这里的整数n是RSA 算法的模;
3)Bob 再选择一个随机数e∈N,这样1 4)使用扩展欧几里德算法,计算出d∈N,且1 5)Bob 在一些公共数据库中发布(n,e),但不发布d、p、q和φ(n),因此,Bob 的公钥为(n,e),私钥为d,或者被称为它的解密指数。 假设明文消息m∈M是数值形式,且m 1)Bob 通过公共数据库获得Alice 的公钥(n,e); 2)Bob 通过加密算法对消息m进行加密,c≡me(modn); 3)Bob 发送c∈X给Alice。 当Alice 接收到加密消息c时,使用m≡cd(modn)进行计算。 RSA 的主要应用之一是数字签名,在这里,数字签名是一种将信息绑定到实体的机制,并且包含一个验证过程[9]。讨论的第一个签名方案是消息恢复方案,这意味着发送的消息不需要作为验证算法的输入,在这种情况下,原始消息可以从签名本身恢复[10]。 1)初始化阶段 Alice 发送消息给Bob,从RSA 密钥空间k={n,p,q,e,d}选择签名所需要的各种参数。 2)签 名 Alice 的私有数字签名Sigk由下式生成: Verk是它的公共验证算法,然后它发送(m,c)给Bob。 3)验 证 Bob 获得Alice 的公钥及签名信息(e,Verk),计算Verk(m,c),当m≡ce(modn)时,Verk(m,c)正好是1,在这种情况下,Bob 接受签名,否则拒绝它。 PyCryptodome 是一个包含底层密码原语的Python 包,该文基于Python3.7 以及PyCryptodome 密码包,软件环境为Win7、Pycharm。 1)Cryptodome.Cipher:包含保护数据机密性的算法,有3 种加密算法:对称加密、非对称加密和混合加密[11]; 2)Cryptodome.Random:返回长度为N的随机字节字符串; 3)Cryptodome.PublicKey:系统定义了一个密钥对,其中一个是机密的(私钥),另一个是可以公开的(公钥); 4)Cryptodome.Hash:哈希函数,以任意二进制字符串为输入,生成随机的固定长度输出,又称为消息指纹或哈希值[12]; 5)Cryptodome.Signature:数字签名的算法,用于保证完整性和不可否认性。 3.2.1 生成密钥对 使用非对称密码算法时,Bob 首先要随机生成一对密钥,下面代码是Python 的RSA 密钥对生成过程,公钥存储在文件Bob_public_key.pem 中,私钥存储在文件Bob_private_key.pem 中,程序代码如下: 3.2.2 RSA数据加密 Alice要向Bob发送加密的数据,假设Alice已经获得Bob的公钥,且存储在一个名为Bob_public_key.pem的文件中。因为希望能够加密任意长度的数据,一般使用混合加密方法,即使用AES 加密消息明文,再用RSA 加密随机生成的会话密钥,使用EAX 模式[13]来检测未经授权的修改。过程如下: 3.2.3 RSA解密算法 Bob 首先使用自己的私钥解密,获取会话密钥,然后进行密文解密。具体算法如下: 3.2.4 RSA数据签名 发送者Bob 使用自己的私钥对消息进行签名,接收者Alice 使用Bob 的公钥对签名信息和完整性进行解密及真实性验证[5]。 假设明文为: 同理,接收方首先使用自己的私钥解密并获得对称密钥key,然后对密文Encrypt_text 解密获得明文Message,这里不再赘述。 无论设计的算法有多安全,攻击者总会想办法破解或绕过它们,每种算法都有其局限性,加密和破解永远是一对矛盾。RSA 当然也不例外,有其弱点,从以下几个方面对其安全性进行分析。 RSA 密码算法的安全性是基于大整数因子分解难题[14](The Integer Factorization Problem,IFP),其中,p和q是两个不同的大质数,如果求出p和q,那么就可以通过ed≡1、φ(N)=(p-1)(q-1)等计算出私钥d。也就是说,任何能够因式分解N的人员都可以通过计算C=Me的逆M≡C1/e(mod(p-1)(q-1))(modN)来破解RSA 密码算法,即如果给出N的质因数分解,那么RSA 算法问题可以在多项式时间内求解。因子分解问题的进展情况如表1 所示。 表1 因子分解问题的进展情况[3] 最近的研究表明,破坏RSA 可能比分解更容易,但也有证据表明,破坏RSA 可能与分解一样困难,因此,破坏RSA 最直接的方法是因式分解RSA 模数N,常见的关于RSA 整数因子分解的方法有费尔马因子分解、二次筛攻击等。 美国普渡大学计算机科学教授Samuel 说:“如果能很快地计算出离散对数,也就是说,如果能在一个很大的有限域中解出方程ax=b,许多密码系统就能被破解”[15]。离散对数计算问题[16](Discrete Logarithm Problem,DLP)是计算数论、代数的基础,也是公钥密码学研究的重要问题。一个离散对数问题符合式子[4]: 现代数学证明,DLP 在计算上是难以处理的,常见的密码系统,如Diffie-Hellman 密钥交换方案、ElGmmal 密码系统[6]和数字签名算法DSA 的安全性是基于DLP 的难处理性。因此,对于RSA 的因式攻击来说,离散对数攻击也是所有基于DLP 密码系统中最直接的攻击。RSA 密码系统是基于大整数因子分解的密码系统,离散对数攻击也是最直接的威胁。如果攻击者掌握了一种有效的大整数因子分解方法,就能够在多项式时间内分解N=pq,并且计算d≡1/emod((p-1)(q-1)),从而计算C≡Md(modN)。 随着量子计算的出现,计算机运算速度得到了几何级增长,因此破解现代密码体系也不是不可能,据估计,这类计算机的诞生还需要10 年甚至更长时间[6]。2015 年8 月,美国国家安全局宣布,计划在“不久的将来”过渡到一种新的密码套件,可以抵抗量子攻击[4]。 值得注意的是,以上所有的操作都可以由量子算法在量子计算机上有效执行,而经典算法不能在目前的电子计算机上有效执行。在量子计算机上可以在多项式时间内完全破解RSA,也可以在多项式时间内完成IFP、DLP、ECDLP等问题的快速求解[17]。 以上针对RSA 攻击的一个共同特点是它们都直接针对RSA 算法的弱点,然而,有大量的攻击并不直接针对RSA 算法,也就是说,不尝试因式分解模N,这些攻击称为间接算法攻击。比如中间人攻击[4],假设Bob 想和Alice 交流,但间谍Eve 截获了它,然后,他可以用自己的公钥替换附加在电子邮件中Bob 的公钥,然后把它发给Alice。当Alice 用假的公钥加密回复邮件时,Eve 又会截获消息并解密(因为Alice 用间谍Eve 的公钥加密了信息,而不是Bob 的公钥)阅读,然后Eve 用Bob 的实际公钥对回复邮件重新加密并发送给Bob。同理,Eve 对Alice 发送给Bob 的任何信息也可做同样的处理。 RSA 是目前使用广泛的一种公钥密码系统,它的安全性基于大整数因子分解难题[8]。该算法已经受了30 多年的攻击,且生成密钥长度由以前的1 024位发展到现在的2 048 位和3 072 位[9],因此对于当前信息安全保密程序设计来说,它被认为是相当安全的[18]。RSA 密码系统可用于机密性(加密)和身份验证(数字签名),由于签名和解密要比验证和加密慢得多,密码强度主要与RSA 模数N的长度有关,目前长度是2 048 位,即256 字节,相当安全。近年来,计算机语言发展很快,目前较流行的编程语言有C/C++、java、Go 及.NET 等。RSA 密码算法都可以在这些语言环境中得到实现,2019 年11 月,编程语言流行指数(Popularity of Programming Language,PYPL)11 月份榜单发布,Python语言排名第一,首次超Java 语言[19],这个当然不是偶然的,主要是因为Python 语言简单易学,具有丰富的资源库开源软件,还有其他语言没有的“粘合力”,尤其是与大数据、人工智能等的无缝结合[20],所以,在Python 语言环境中实现密码学编程是大势所趋。2.2 RSA加密算法
2.3 RSA解密算法
2.4 RSA数字签名算法
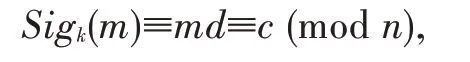
3 基于PyCryptodome的RSA设计与实现
3.1 PyCryptodome库相关函数
3.2 RSA加密算法设计




3.3 消息内容的AES加密与解密

4 RSA算法安全性分析
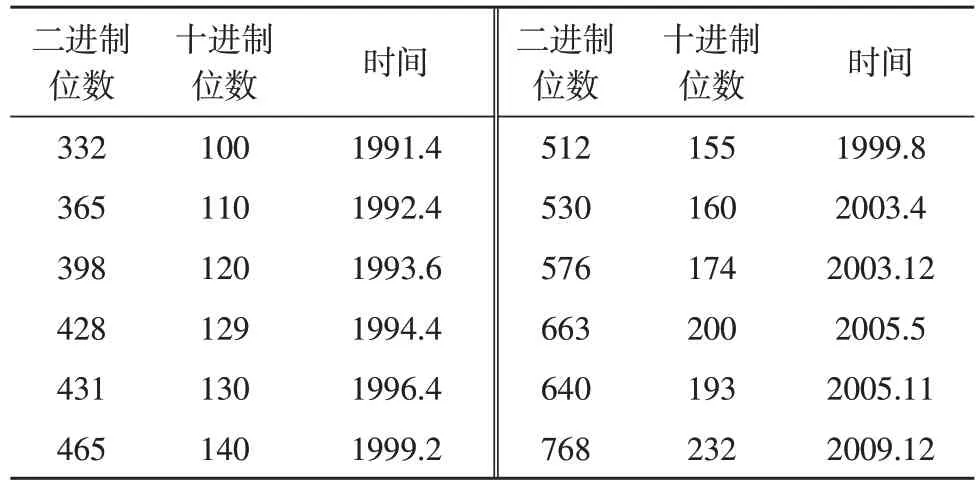
4.1 大整数因子分解攻击
4.2 离散对数攻击法
4.3 量子计算机攻击
4.4 中间人攻击
5 结束语
