进化树突状神经元模型

徐 哲，雷振宇，王子谦，孟祥莲，周 瑜，高尚策

（1.常州工学院计算机信息工程学院，江苏常州 213032；2.富山大学工学部，日本富山 930-8555）

随着科技的发展，工程问题变得越来越复杂。由于这些复杂非线性问题都定义在高维度空间，传统的方法不能有效地解决这些问题。一些学者则利用人工神经网络模拟生物神经网络的信息处理机制去解决这些复杂问题。人工神经网络对非线性问题有很好的拟合效果，已经成功用于图像识别、语言识别、文本分类等问题。为了解决更复杂的问题，许多学者也提出了许多不同的神经网络，如循环神经网络[1]、卷积神经网络[2]、前馈神经网络[3]、树突状神经元模型。其中，树突状神经元模型模拟了一个神经元信息传递的过程。由于其易于解释、实现简单等特点已经被许多学者用来解决各种复杂问题，如预测问题[4]、分类问题[5]等。一些学者则利用非BP 学习方法来训练网络模型[6]。

进化计算是受自然启发的启发式算法，其模拟自然界中生物的生活模式去求解问题，例如粒子群算法(Particle Swarm Optimization，PSO)是模仿自然界中鸟群、鱼群的集体行为，通过不断地对精英个体和自身经验的学习去探索问题解[7]。重力搜索算法(Gravitational Search Algorithm，GSA)是模拟牛顿的万有引力定律，每个个体拥有质量并且通过个体间的相互作用去探索整个搜索空间[8]。差分进化(Differential Evolution，DE)是通过一系列的变异、杂交、选择等操作，寻找更优解[9]。进化计算已经应用于很多工程问题，如模式识别[10]、控制工程[11]、土木工程[12]等。文中利用进化计算的算法训练容易理解的树突状神经元模型。

1 树突状神经元模型

1.1 突触层

突触层是一个神经元连接到另一个神经元或者细胞体的相互接触的结构。神经元通过突触将信号传递给下个神经元或者细胞体，这时神经元或者细胞体则由于不同的阽危呈现抑制状态或者激活状态。将这些不同的突触组合成突触层来接收外界的信号，第i个突触连接到第j个突触层被定义为式（1）：

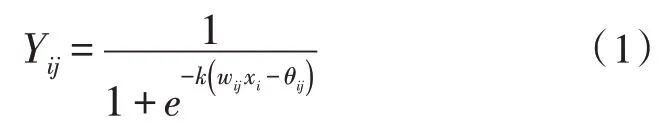
其中，Yij是第i个突触在第j个突触层上的输出，k是一个正常数，xi是第i个突触上的输入，wij和θij分别是学习的权重和阈值。

根据不同的权重和阈值，神经元与神经元或细胞体之间有4 种不同的连接状态：常0 状态，与输入无关；常1 状态，此时输出为恒定值1，与输入无关；抑制连接，此时输入与输出成反比；兴奋连接，此时输入与输出成正比。

1.2 树突层

树突层接收突触层的各个突触传入的信号，由于突触的非线性，树突层采用乘法操作来处理非线性信号。这种乘法操作即为逻辑AND 操作，定义为式（2）:

其中，N是突触层数量，Yij是突触层输入。

1.3 膜 层

膜层接收每一个树突传来的信号，通过求和操作处理后传递给胞体层。这种求和操作即为逻辑OR 操作，定义为式（3）:

其中，M是树突层数量，Zj是树突层输入。

1.4 胞体层

信号通过层层处理，胞体层接收膜层的信号，利用sigmoid 函数给出最终的结果，胞体层定义为式（4）：

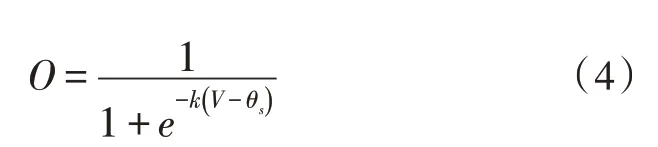
其中，k是一个常数，V是膜层处理的输入信号，θs阈值由0 变到1。

2 进化计算

针对高维度、非线性、不可微的复杂问题，许多学者受自然启发提出了许多启发式算法，如差分进化(DE)[13]、重力搜索算法(GSA)[14]、粒子群算法(PSO)[15]等。许多学者也已经证明了启发式算法能够解决高维度、非线性的问题。

进化计算与传统BP 训练神经网络[16]的目的都是通过调整权重和阈值减小模型误差。进化计算按照网络模型的结构随机初始化一个种群，这个随机种群包含了模型的权重和阈值。这些权重和阈值决定模型层之间信息的传递，决定最终的输出。种群被随机初始化，其中个体代表一组网络的权重和阈值，定义为式（5）：

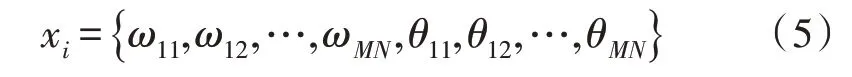
进化计算优化的目标函数则是模型输出结构目标结果的误差。其目标函数定义为：

其中，P是训练样本的个数，Tp是第p个样本的目标，Op是第p个样本真实的网络输出。

2.1 粒子群算法（PSO）

粒子群算法是受鱼群、鸟群启发，模拟自然界的群体行为，每个个体有他们自己的速度和位置，粒子的位置也代表了潜在的解。每个种群中有当前全局最优解和每个个体的最优解。利用全局最优和个体最优来更新粒子的速度和位置去探索，如式（7）和式（8）所示。

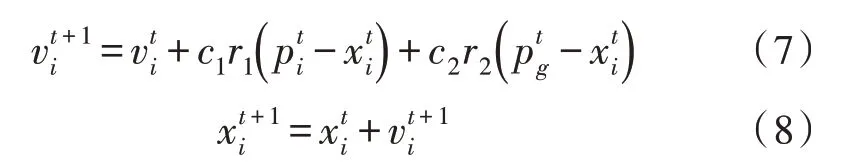
其中,c1和c2是两个正常数，vi是区间(0,1)内的随机数,是粒子在时刻t时的历史最优位置，粒子通过向自己最优和全局最优学习来更新自己的位置。通过式（6）作为优化目标不断地更新粒子的位置，直到达到终止条件。粒子群算法的易于实现、稳定等特点已经用来解决许多非线性问题。

2.2 差分进化（DE）

差分进化是一个简单有效的进化算法，进化计算类似于一般的进化算法通过编译、交叉和选择来搜索解。进化计算的基本流程为按照式（5）随机初始化种群，基于当前种群通过差分策略生成变异向量，进行杂交操作形成子代种群，选择子代中优于父代的个体留在新的种群中。

变异操作是基于当前种群利用不同差分策略产生变异个体的，例如：

其中，下标r0、r1 和r2 是在集合{1,2,3,…,NP}中选取的随机数；xbest是当前种群中最好的个体；Fi是常数，用来控制差分幅度。

交叉操作在变异操作后定义为式（12）：

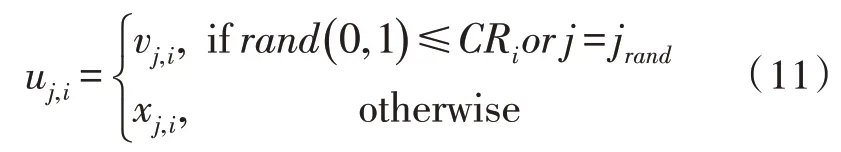
其中，CRi是交叉概率，rand(a,b)是在区间(a,b)上随机取一个整数；jrand是随机在(0,1)上随机选一个整数。

选择操作根据目标函数的适应度在父代和子代选择更好的个体构成新的父代，定义为式（12）：

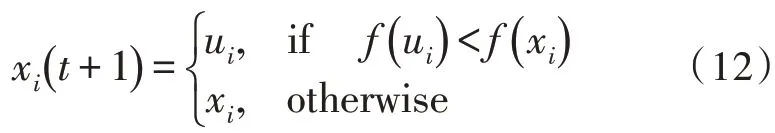
其中，f()∙是目标函数的适应度即式（6）。

2.3 重力搜索算法（GSA）

重力搜索算法可以看作基于种群的启发算法，重力搜索算法是基于万有引力定律启发，利用万有引力定律和牛顿第二定律，计算粒子的加速度去更新粒子的速度、位置。

重力搜索算法利用式（5）随机初始化种群，将神经网络中的权重和阈值作为有质量的粒子并通过万有引力更新它们的位置。粒子xi和粒子xj之间的万有引力被定义为式（13）：

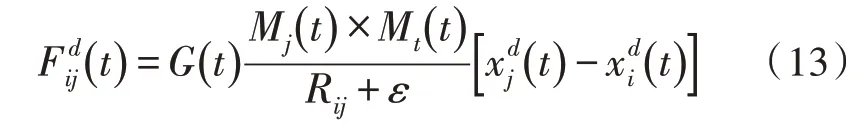
其中，G(t)是万有引力常量，Rij是粒子xi和粒子xj之间的欧氏距离，Mi(t)和Mj(t)分别是粒子xi和粒子xj在t时刻的重量。GSA 通过重力不断更新粒子位置，搜寻最优个体。GSA 流程图如图1 所示。

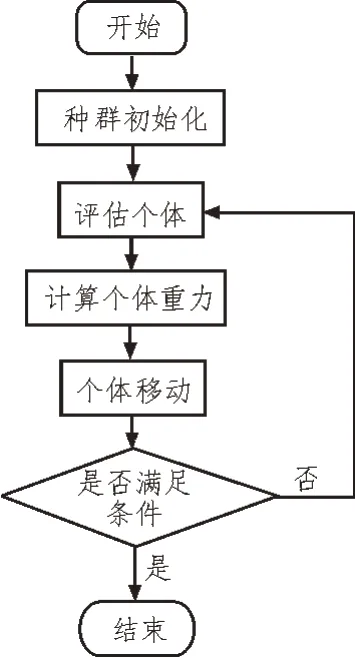
图1 GSA流程图

重力搜索算法将权重和阈值作为空间中有质量的个体，不断地更新个体的位置，直到达到终止条件。

3 实验分析

文中将神经网络与进化计算进行了结合，提出了进化神经网络。在进化神经网络中，神经网络使用进化算法训练。神经元之间的权重和阈值被随机初始化，然后通过进化算法进行优化，减小网络的误差。

为了验证进化计算在神经网络训练上的有效性，PSO、GSA、DE 用来训练神经网络，在不同的分类数据集XOR、Balloon、Iris 和Heart 中验证进化计算在神经网络训练中的鲁棒性。表1 描述了详细信息。

表1 数据集详述

针对不同的数据集，树突状神经元模型的参数包括树突层数量M、阈值θ和k。不同的参数，模型的泛化能力不同。通过正交实验法，确定了网络模型的参数，确保更优地解决拟合问题，其参数设置如表2 所示。

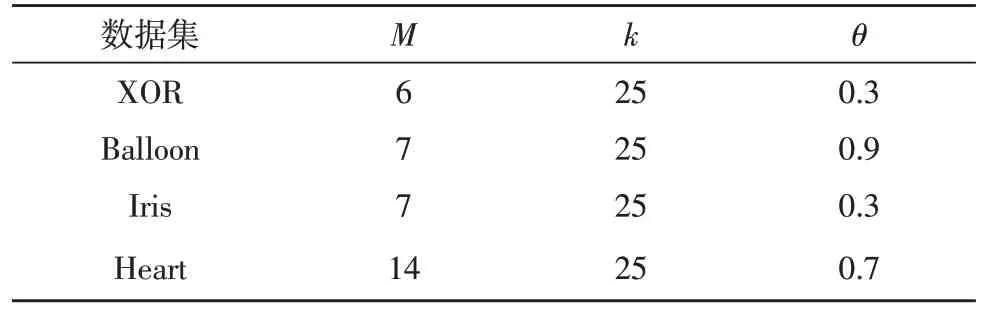
表2 神经网络模型参数设置

进化计算代替传统的BP 学习去训练神经网络的权重和阈值，文中用DE、GSA、PSO 训练树突状神经元模型。表3 记录了DE、GSA 和PSO 与传统BP 的实验结果，包括30 次实验的均值、标准差和p值。

通过表3 可以发现，进化计算在所有的数据集上都优于传统BP 学习，拥有更小的误差。此外，Heart 数据集上的收敛图为图2。由于进化算法和传统BP 的迭代次数不同，给出了进化计算的收敛因子图，方便观察。通过收敛图可以发现，进化计算收敛速度明显优于传统BP。不同的进化算法也存在差异，因此，选择合适的进化计算算法也是十分重要的。

表3 进化计算与传统BP的实验结果

图2 Heart数据集的收敛图

箱线图能够更直观地展现算法的稳定性和收敛效果。通过图3 可以观察到进化计算能够搜索到更优解，并且有较强的稳定性。

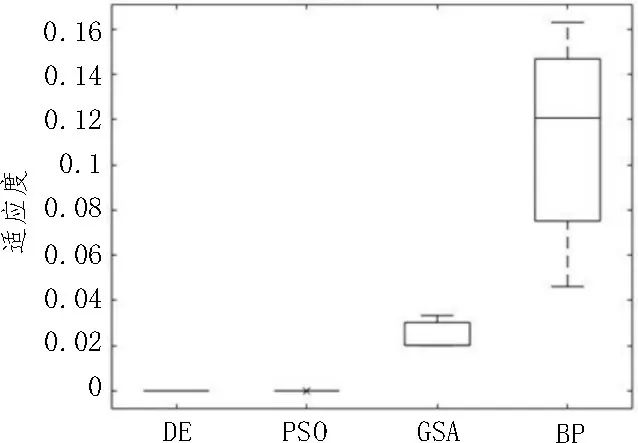
图3 Heart数据集的箱线图

实验表明，进化计算能够代替传统的BP学习训练神经网络，并且进化计算能够取得更优的结果[17-19]。

此外，树突状神经元模型，由于神经元之间的连接有4 种不同的状态，因此可以根据连接状态进行裁剪并用逻辑电路实现。GSA 训练的Heart 数据集的最终网络模型利用逻辑电路呈现，如图4 所示。

图4 裁剪后的神经网络的逻辑电路图

通过图4 可以发现，树突状神经元很容易利用逻辑电路实现，而且通过裁剪大幅度优化了网络的复杂度，更加容易理解。同时可以发现GSA 训练的神经网络模型减少了树突层的个数，由原始的七层减少到了两层。

4 结束语

文中用进化计算算法训练树突状神经元模型，并在不同的数据集上进行测试。结果表明进化计算比传统的训练方法更有效。在未来工作中，仍能改进计算算法，进一步提高训练精度。