基于测压管数据的某水库土坝渗流安全性分析

2021-08-20刘凤茹波兰汗开肯詹达美

人民珠江 2021年8期

刘凤茹，波兰汗·开肯，詹达美

(1.深圳市广汇源环境水务有限公司，广东深圳 518020;2.河海大学水利水电学院，江苏南京 210098)

大坝安全一直是水利工程领域重点关注问题，尤其是大坝渗流安全是大坝安全评价的重要组成部分[1-2]。坝体渗流通常对混凝土坝和坝基岩土产生化学侵蚀破坏，而对土石坝可能产生渗漏或管涌等严重的渗透破坏[3-4]。据相关统计[5-7]，在美国206座破坏的土坝中，管涌和渗透破坏导致溃坝占52.5%；在中国存在严重渗漏的大型水库132座，其中土石坝占80%左右，在大型水库发生的事故调查中，渗漏管涌破坏占31.7%。可见，大坝渗漏问题是影响大坝安全的重要因素，因此有必要对大坝，尤其土坝开展渗流分析及渗透稳定性判别[8-11]。

土坝渗流分析有水力学解析法、流体力学解析法和数值解法等，而目前常用的方法是数值解法，主要包括边界元法、有限单元法和有限差分法等[12-14]。可以通过计算获得过渗流水头线、渗漏量和渗透坡降等参数，对坝体进行渗流安全分析。本文在对某水库大坝测压管实测资料分析的基础上，利用有限单元法对大坝进行渗流安全性计算分析和综合评价。

1 渗流计算方法

1.1 渗流计算原理

假设坝体符合平面假定，采用二维饱和渗流场基本方程为：

(1)

式中x、y——主渗透方向；kx、ky——主渗透系数；H——水头。

对于平面问题的四边形单元，单元内的水头分布为：

(2)

应用变分原理将微分方程(1)转化为有限元计算格式：

[k]{H}={Q}

(3)

式中 [k]——总传导矩阵；{Q}——计算区域边界上的分布流量的等效节点流量。

(4)

式中 [k]——e单元的传导矩阵；[Be]——单元的形变矩阵；Ω——计算域。

对每个可能包含自由面的单元，逐个高斯点计算水头，当计算水头值小于其位置水头时，按式(5)计算该高斯点对该单元各节点初流量的贡献。

{Ω}e=-[B][K][B]

(5)

(6)

则第r次迭代的水头值为：

{Hr+1}={Hr}+{ΔHr}

(7)

1.2 渗透稳定性判别

无论是流土还是管涌，一般采用渗透坡降来判别渗透稳定性。其中，临界渗透坡降根据《水利水电工程地质勘察规范》推荐的公式进行计算[15]：

流土型Jcr=(Gs-1)(1-n)

(8)

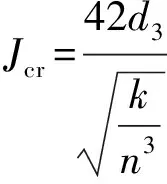
(9)

式中Jcr——土的临界渗透坡降；Gs——土的颗粒密度与水的密度之比；n——土的孔隙率；k——土的渗透系数；d3——小于该粒径占总土重3%的土粒粒径。

2 实例分析

2.1 工程概况

某水库大坝原为均质土坝，于1957年10月动工兴建，1958年基本建成，后经过多次加固与修复处理，并于1989年在坝轴线上游侧老坝体增设0.7 m厚混凝土防渗墙；2013年除险加固对坝基、坝肩采用帷幕灌浆进行防渗处理，并对大坝下游坡进行培厚。大坝上游坝坡为混凝土护坡；大坝下游坡为草皮护坡，分别在高程28.59 m和22.68 m处设有宽为2 m的一级马道和二级马道，排水棱体顶部高程为20.0 m，棱体外坡比为1.0∶1.5，顶部平台宽2 m，排水棱体后设量水堰。除险加固后的大坝断面见图1。

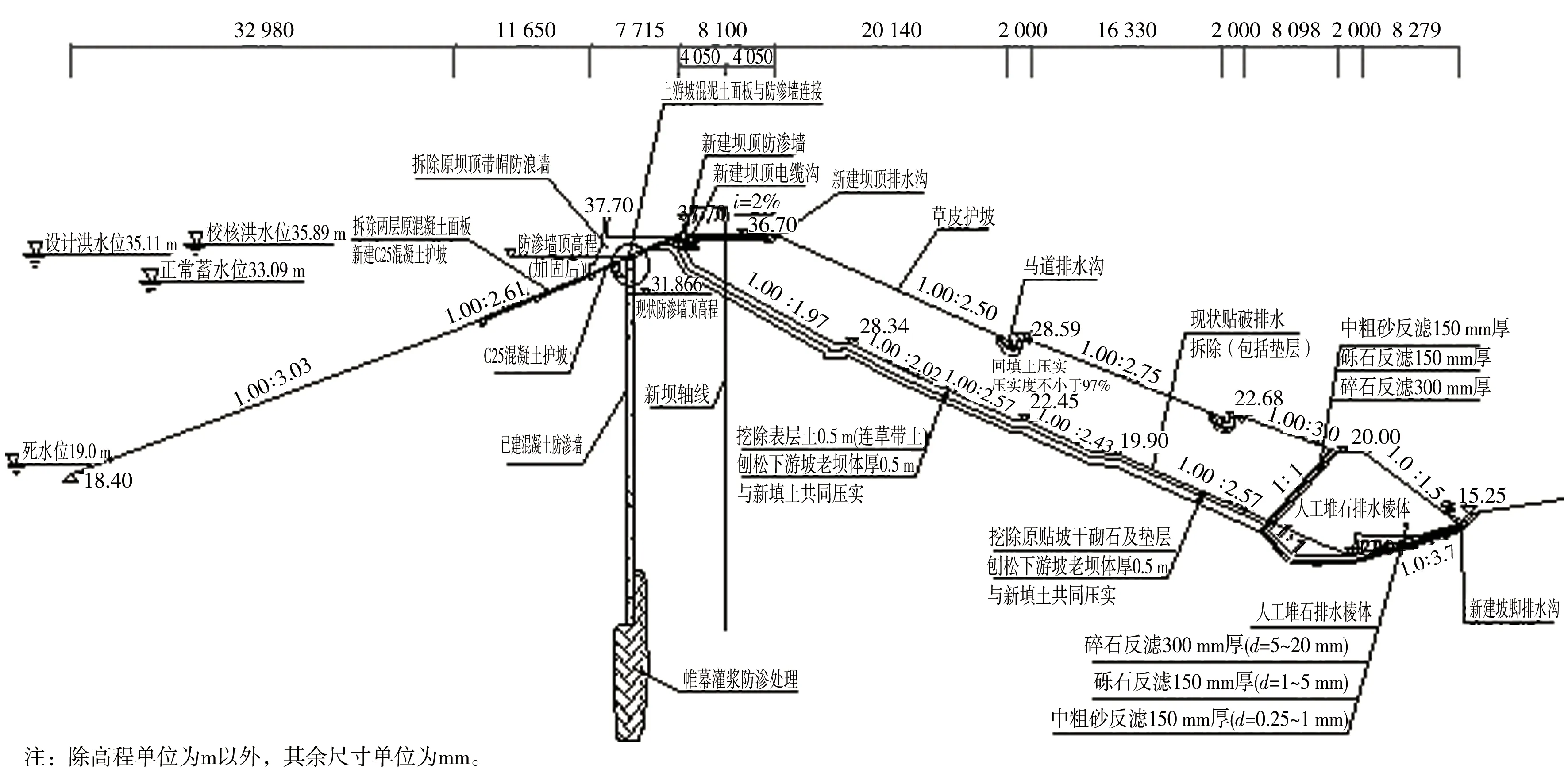
图1 除险加固的大坝断面

2.2 渗流观测数据分析

图2为水库大坝监测设施平面布置，共设置4个观测横断面，本次以测压管编号为CY5、CY6、CY7和CY8的观测断面作为研究断面。采集了2014年1月至2018年10月份的水库运行水位数据与测压管水位数据资料，绘制随时间的变化曲线(图3)。

由图2、3分析可知，各时间节点库水位大于各测压管(CY5、CY6、CY7和CY8)水位；随着测压管位置与上游坝脚距离的增大，水位逐渐减小，说明坝内水头逐渐削减；位于防渗墙上游侧的CY5测压管水位明显大于下游侧测压管(CY6、CY7和CY8)水位，说明混凝土防渗墙防渗效果较好；CY5、CY6、CY7测压管水位变化趋势与库水位变化趋势基本一致。由于CY7对水位敏感，CY8位于下游对水位不敏感，导致了库水位骤降局部时段产生了CY7低于CY8的滞后效应。测压管数据总体上合理性较好，库水位越高，浸润线越高；从上游到下游，坝内水位沿程不断降低，在混凝土防渗墙处有明显降落，说明防渗墙起到了显著的防渗作用。混凝土防渗墙之后坝体浸润线较为平缓。

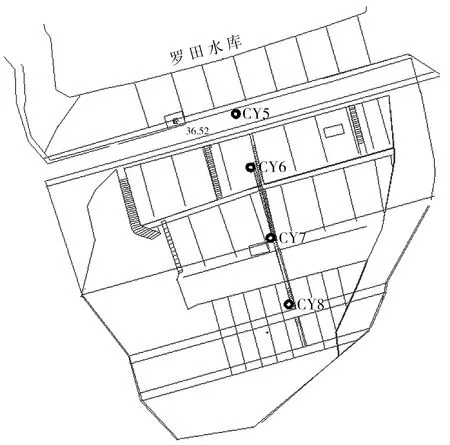
图2 水库监测设施平面布置

图3 2014年1月至2018年10月测压管水位与库水位关系

2.3 坝体渗流特性分析

2.3.1计算工况及参数选取

大坝渗流场计算考虑水库运行中出现的各种不利条件，选取了正常蓄水位、设计洪水位和校核洪水位3种稳定渗流工况和设计洪水位降至死水位、校核洪水位降至死水位2种非稳定渗流工况(表1)。坝体渗流场计算参数见表2。

表1 渗流稳定计算工况

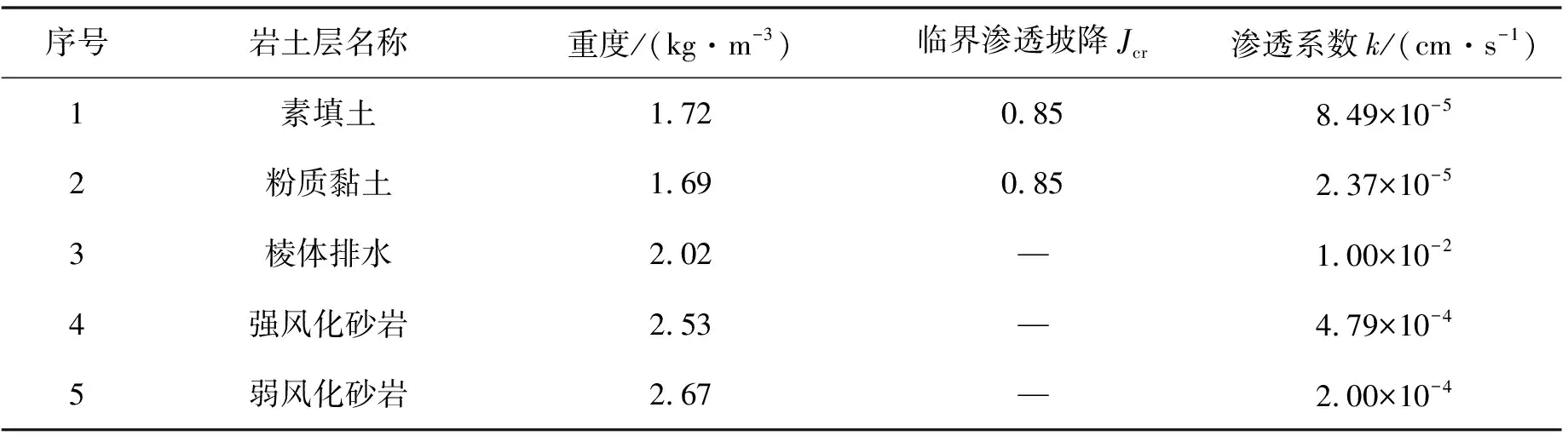
表2 渗流稳定计算参数

2.3.2渗流计算结果与分析

计算得到各工况下大坝等水头线和浸润线见图4，单宽渗流量和出逸点渗透坡降见表3。

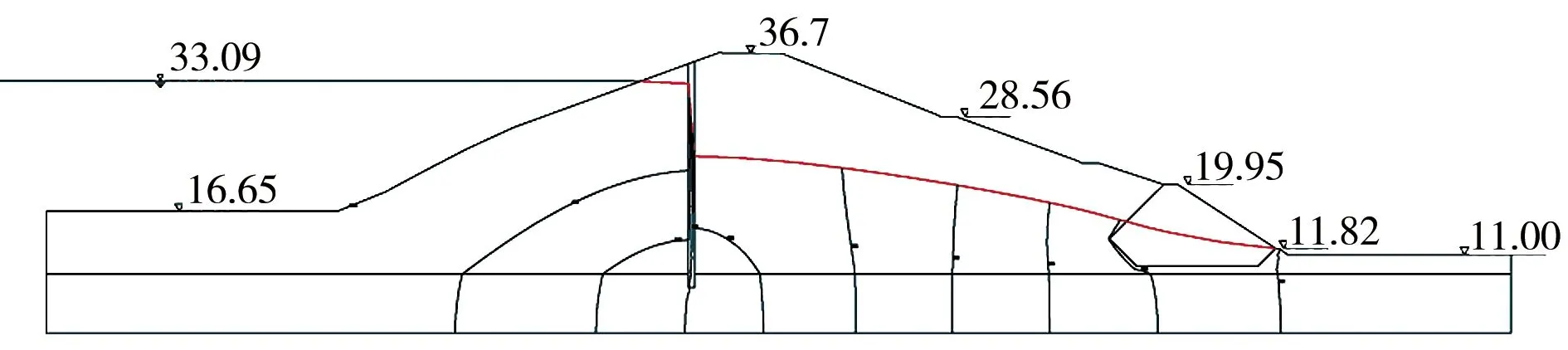
a)工况1 b)工况2

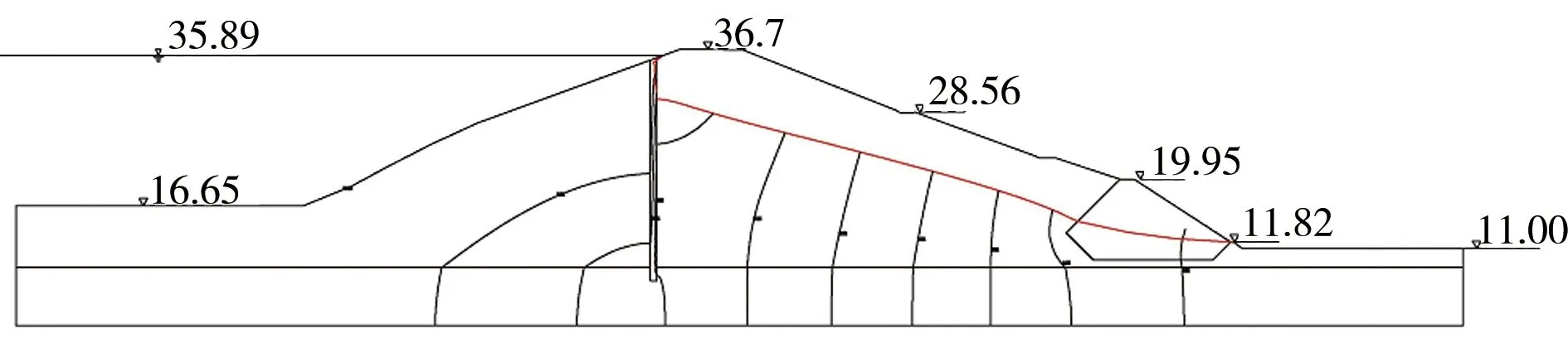
c)工况3 d)工况4

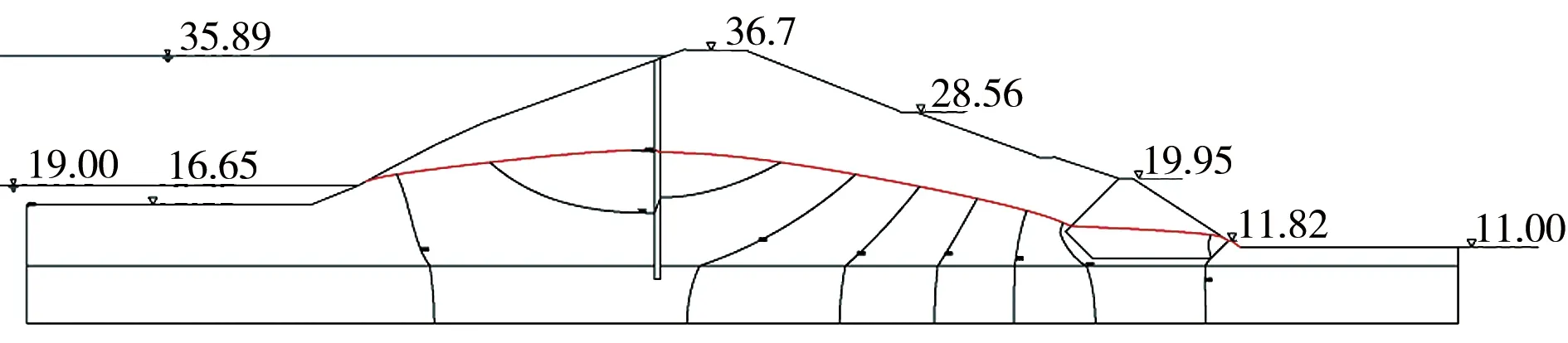
e)工况5

表3 大坝渗流计算结果

由图4分析可知，大坝各工况计算断面等水头线在材料分区处发生偏折，在混凝土防渗墙处密集，浸润线在防渗墙处跌落，浸润线逸出点位置降低，并全部进入排水棱体，符合心墙坝的一般渗流规律。在稳定渗流(工况1—3)中防渗墙能够有效降低浸润线，而在非稳定渗流(工况4、5)中，浸润线降低幅度减弱，但浸润线高度和浸润线逸出点高度相对较低，说明混凝土防渗墙防渗效果较好。计算浸润线与测压管观测数据基本一致，在稳定渗流场情况下，库水位越高浸润线越高，库水位越低浸润线越低，计算结果均能合理反映。

根据表3分析可知，稳定渗流(工况1—3)和非稳定渗流(工况4、5)中，均存在随着库水位的升高，最大单宽渗流量升高，而非稳定渗流的最大单宽渗流量小于稳定渗流工况的情况。此外，随着水位变化，关键部位的渗透坡发生相应变化；稳定渗流的逸出坡降小于非稳定渗流工况。非稳定渗流的工况5逸出渗透坡降最大，为0.36，但小于坝体填土允许坡降0.85，不会发生渗透破坏，大坝的渗流稳定性满足要求。