基于模糊层次分析法的工业机器人可靠性分配

胡钧铭，黄洪钟，黄 鹏

(1.电子科技大学机械与电气工程学院，成都 611731；2.西华大学汽车与交通工程学院，成都 610039；3.电子科技大学系统可靠性与安全性研究中心，成都 611731)

可靠性是保障工业机器人安全有效运行的重要质量特性，是工业机器人研发的关键指标。在研发阶段，通过可靠性分配将工业机器人的整机可靠性指标合理分配到各子系统，对明确各子系统可靠性研制要求、权衡系统研制方案、统筹项目进度具有重要指导意义。作为工业机器人研发的关键步骤，可靠性分配需要综合考虑多种可靠性分配影响因素，如技术复杂度、维修性、故障危害性等。因此，可靠性分配可视为一个多属性决策问题。

作为一种有效的多属性决策问题分析工具，层次分析法运用层次结构将复杂问题解构，通过对低层级各元素相对上一层级某个元素进行两两比较，将元素间的相对重要性量化为判断矩阵，随后由判断矩阵推导各备选方案的权重并整合到目标层[1]。但限于数据和经验，层次分析法判断矩阵中的两两比较不可避免地具有主观性和模糊性。为解决层析分析法判断矩阵成对比较的主观性强的问题，相继提出了区间层次分析法[2-3]、区间粗糙数层次分析法[4]以及层次分析法与模糊综合评价相结合[5-7]等改进方法。在这些方法中，模糊层次分析法将判断矩阵的整数型标度扩展到模糊集合上，是层次分析理论的进一步发展[8]。作为处理模糊信息的有效理论，模糊数学能清晰刻画成对比较中的模糊性。因而，模糊层次分析法广泛应用于公共交通服务质量评价[9]、采煤风险评估[10]、物联网[11]、项目风险评估[12]、关键技术元素识别[13]等多属性决策分析问题中。

现综合考虑影响工业机器人可靠性分配的因素，建立工业机器人可靠性分配的层次结构，运用三角模糊数建立模糊判断矩阵，基于约束模糊运算方法进行权重计算，为工业机器人各子系统排序及可靠性确定提供参考。

1 模糊判断矩阵

1.1 三角模糊数

(1)

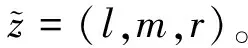
(2)

1.2 模糊判断矩阵

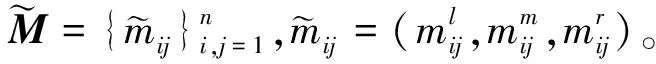
(3)

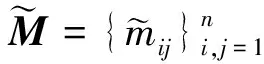
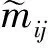
(4)

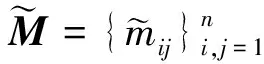
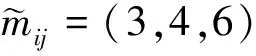
因模糊层次分析法可视为对层次分析法中原整数型标度的模糊扩展，因此建立语义变量与三角模糊数标度间的对应关系如表1所示。

表1 整数标度模糊扩展

1.3 权重确定

(5)

(6)

(7)

显然该算法中保留了模糊判断矩阵的互反关系，充分利用了模糊判断矩阵所具备的信息。

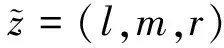
(8)

2 工业机器人可靠性分配

依据功能，工业机器人可以分为本体、驱动器控制器、减速器和伺服电机5个关键部件。整机功能的实现有赖于5个部件的协调配合，系统可靠性可以视为5个关键部件的串联模型。

2.1 层次模型建立

工业机器人可靠性分配需要首先建立工业机器人的层次结构模型。它主要包括可靠性分配的目标层O、准则层C和方案层A。将目标层O设定为工业机器人可靠性分配的目标值，即将工业机器人的系统可靠性要求作为求解目标；准则层C对应可靠性分配中考虑的各种影响因素；方案层A对应工业机器人的关键部件。建立工业机器人可靠性分配的层次结构如图1所示。

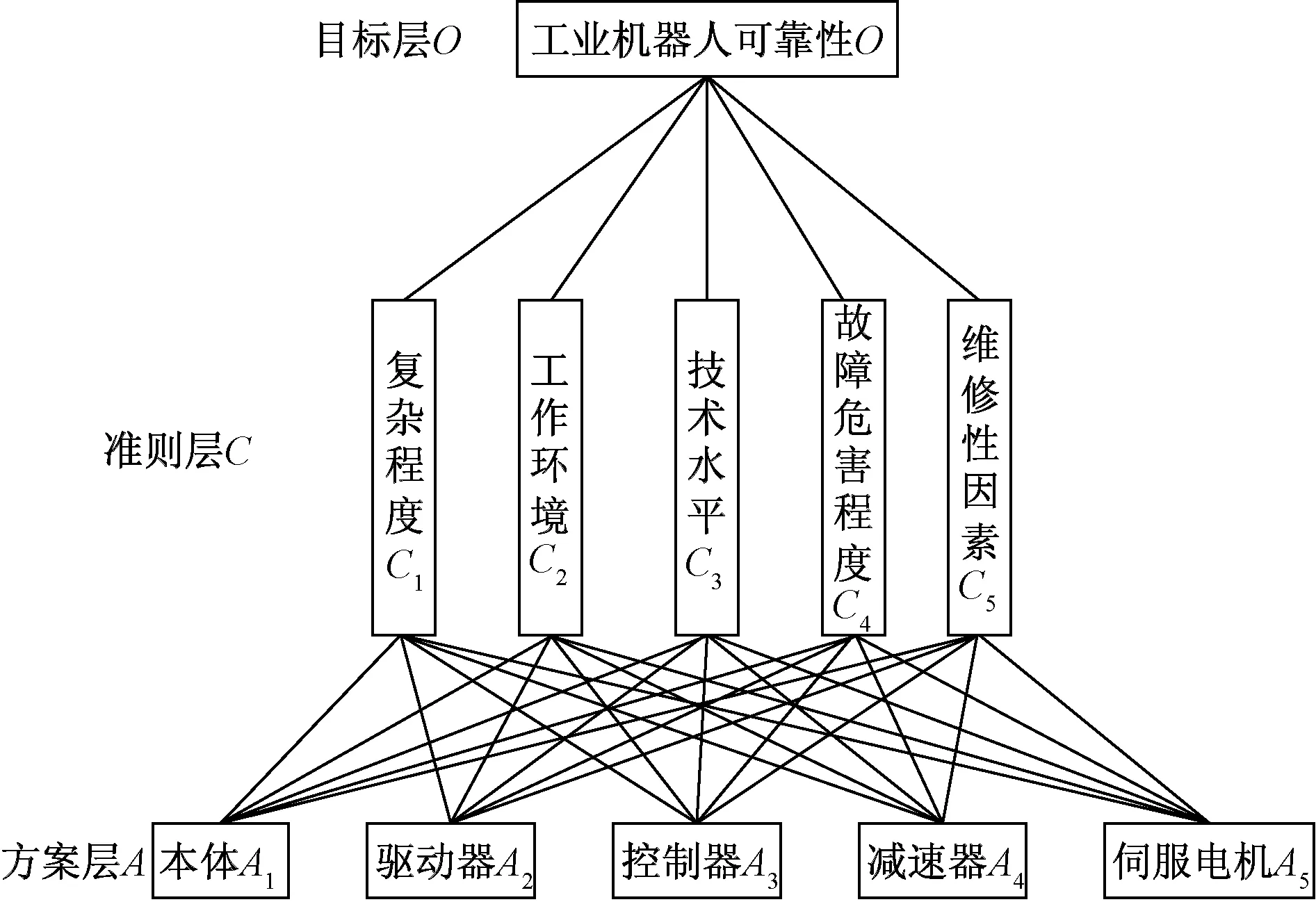
图1 工业机器人可靠性分配层次结构

2.2 判断矩阵构造

通过两两比较，并利用表1设定的三角模糊数标度建立工业机器人可靠性分配各层级的判断矩阵。准则层C相对于目标层O的模糊判断矩阵如表2所示，方案层A相对于准则层各准则Ci的模糊判断矩阵如表3所示。

表2 准测层C相对于目标层O判断矩阵

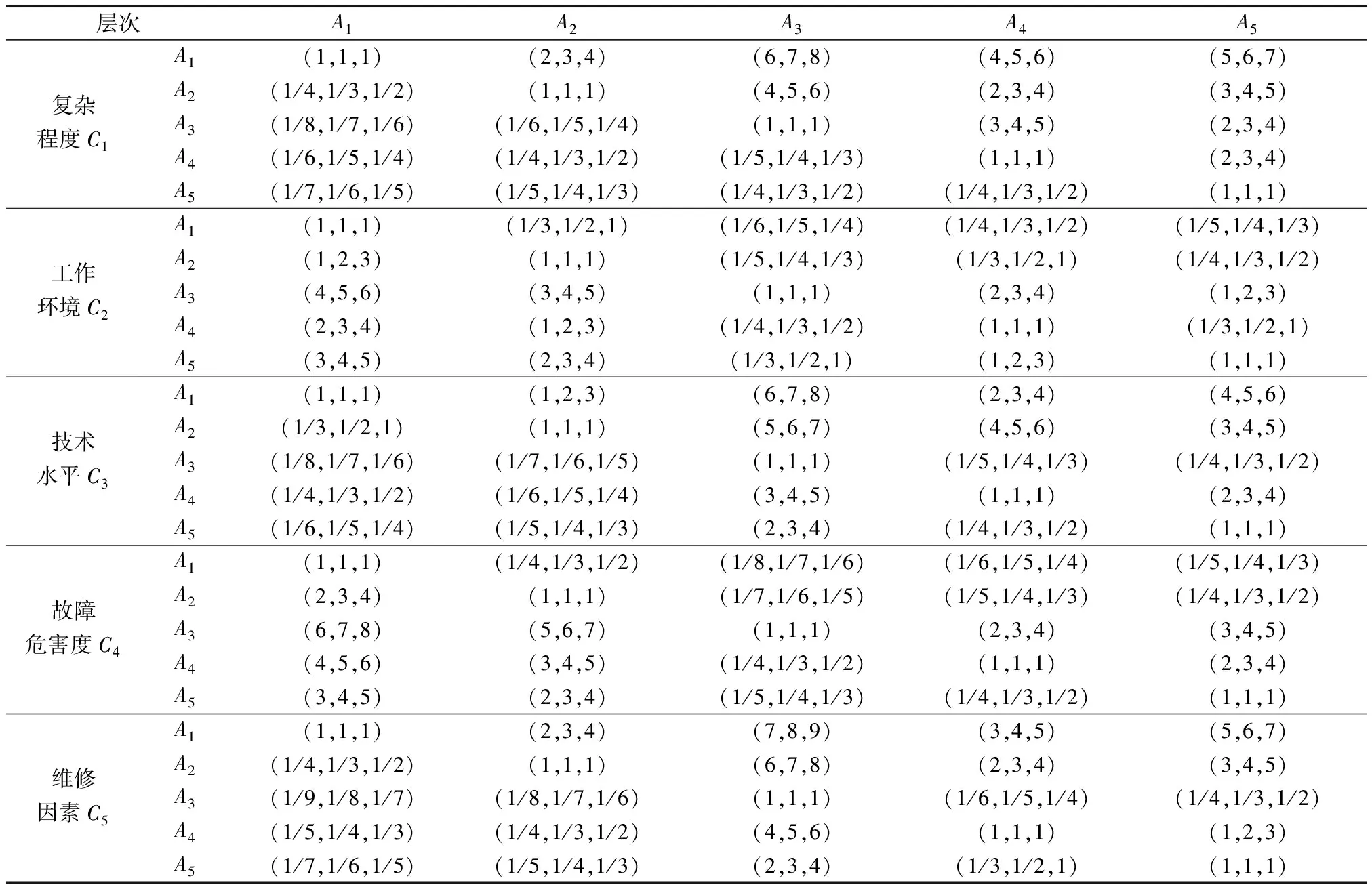
表3 方案层A相对于准则层C判断矩阵

2.3 权重向量计算

利用式(5)～式(7)计算各判断矩阵的模糊权重，并通过式(8)将各模糊权重清晰化，并将清晰化的各级权重进行归一化。表4给出了各准则相对于目标层的模糊权重、去模糊化后的权重以及归一化权重。方案层各方案Ai相对于各准则Ci的权重列表分别如表5～表9所示。

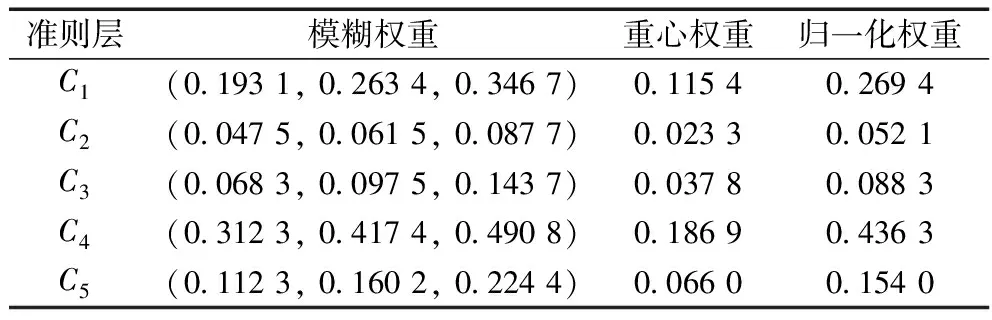
表4 准则层C相对于目标层O权重

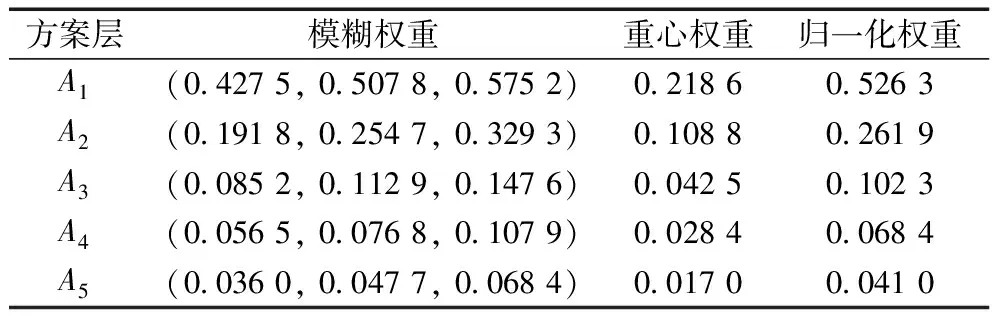
表5 方案层A相对于C1权重

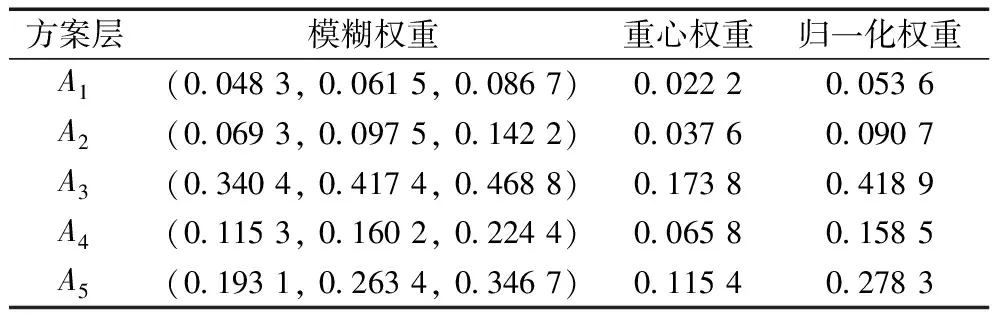
表6 方案层A相对于C2权重

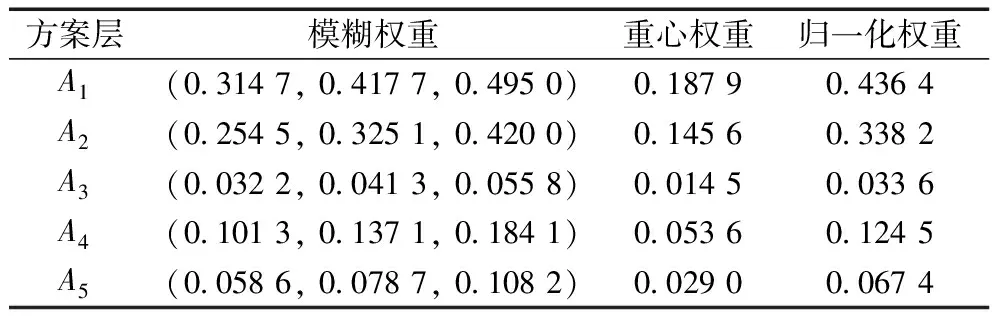
表7 方案层A相对于C3权重

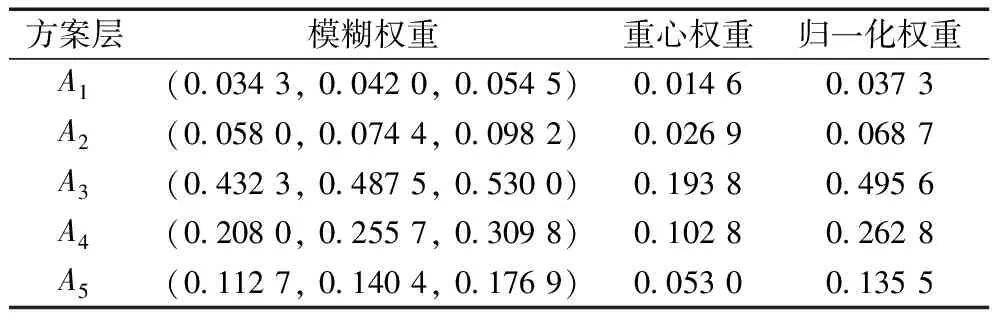
表8 方案层A相对于C4权重

表9 方案层A相对于C5权重

3 可靠性分配

整合方案层权重wC和准则层权重矩阵M可以获得各方案Ai相对于目标层的权重向量w=(w1,w2，…,w5)。综合表4～表9可得

wC=[0.269 4, 0.052 1, 0.088 3, 0.436 3, 0.154 0]，

M=

且

w=wCM=[0.276 5, 0.177 1, 0.273 2, 0.171 8,

0.101 6]

(9)

工业机器人整机可靠性指标设定为平均无故障工作时间MTBF=4 000 h。由串联系统可靠性模型可知，各单元的可靠性分配为

(10)

故本体MTBF1为1.446 8×104h，驱动器MTBF2为2.259 2×104h，控制器MTBF3为1.464 3×104h，减速器MTBF4为2.328 5×104h，伺服电机MTBF5为3.938 4×104h。

4 结论

由于工业机器人可靠性分配需要考虑多种影响因素，运用模糊层次分析法将系统可靠性要求、可靠性分配影响因素与工业机器人各子系统构建成层级模型，便于确定各子系统相对整机可靠性要求的权重，为子系统的可靠性确定提供了参考。

三角模糊数扩展了传统层次分析法中整数标度，改进了传统层次分析法对判断矩阵确定中存在的不精确性量化不足的缺点。同时相较于模糊互补判断矩阵的标度，三角模糊数提供了更为充分的信息。它不仅提供了模糊数的支撑集，而且给出了其出现的可能性。前者包含了相对重要性的未知比率的范围，后者则通过所在范围的隶属度函数来量化。此外，经约束模糊运算改进的几何权重法不再是单一的算数运算，而是保留了模糊判断矩阵的实际意义，使得模糊权重更符合工程实际背景。

结果表明，工业机器人的各子系统中，伺服电机分配的MTBF最大，其次是驱动器和减速器，本体和控制器的MTBF较小。伺服电机、减速器和控制器是影响工业机器人可靠性的关键部件。