基于线性二次调节器算法的两轮自平衡机器人最优控制方法
2021-08-20刘东洋
徐 鑫,刘 彬,刘东洋
(空军工程大学信息与导航学院,西安 710077)
随着科学技术的发展,机器人和自动化产业变得越来越普遍,并与日常生活融为一体。从智能家居到语音交互再到人机共存,人工智能无论是在效率还是在便利性方面都正朝着改善人们生活的方向发展。例如家庭服务的扫地机器人,公共服务的导游,迎宾机器人,工业生产的搬运、码垛、包装机器人,以及国防军事、公共安全方面的特种机器人[1]。
两轮自平衡机器人作为一类具有两个独立制动的车轮的自平衡机器人平台,其重心位于车轮旋转轴线上方,仅靠两个轮子来实现平衡和灵活的移动,并且它可以帮助用户携带物品运动而不使物品掉落,从而为用户提供一双“额外的手”。在两个车轮上保持平衡是自平衡机器人的核心部分,为了优化这些机器人的平衡机制,开发一种机电控制系统使自平衡机器人能够尽快平衡自身显得尤为重要。
两轮自平衡机器人的运动行为类似于经典的倒立摆机械系统,可以在垂直位置进行平衡。该系统具有固有的不稳定性,即使轻微的干扰也会导致系统跌落。因此,中外众多专家学者提出了多种不同方案,也取得了重要成果[2-6]。杨兴明等[7]分层滑模控制策略推导系统总的控制律,利用模糊逻辑的万能逼近功能进行估计,进一步改善了控制系统的品质。张俊杰等[8]采用模糊自适应控制策略解决了两轮自平衡机器人的模型多样化的自适应运动控制问题。文献[9-10]针对两轮自平衡机器人的参数不确定性开展了基于滑模变结构跟踪控制的研究。宋寅卯等[11]采用线性自抗扰控制解决了两轮自平衡车因不同用户身高体重差异导致系统控制稳定性能差的问题。这些研究取得了很重要的理论成果及应用。当然,自平衡机器人控制系统的研究还逐渐以产品的形式出现在人们的日常生活,例如Segway或Hoverboard平衡车。此外,该类机器人紧凑的结构和良好的机动性在更多方面可以帮助人们日常生活[10-11],它们可以很大,可以在建筑工地周围帮助工人运输混凝土块,它们也可以很小,在办公室内为人们端茶送水、传递文件,例如助理机器人[12]、残疾人轮椅[13]。
为了深入理解两轮自平衡机器人的运动平衡机制并以此来设计控制器,从而实现对两轮自平衡机器人的控制。首先,通过分析自平衡机器人的运动原理;其次,建立系统数学模型并在状态空间实现中表示;此外,设计状态估计反馈控制器使机器人稳定在不稳定的平衡点附近;最后,引入线性二次调节器(linear quadratic regulator,LQR)控制方法得到更好的控制效果。实验结果表明,LQR控制方法对于这类自平衡机器人运动平衡控制具有良好的稳定性和鲁棒性。
1 问题定义与解决方案
1.1 问题定义
倒立摆是控制系统中的经典问题,这类系统的不稳定性和非线性很适合用于探索不稳定的动力学。常见的例子如图1所示。
影响双轮自平衡机器人机体保持平衡和直立的原因可以分为软件和硬件两个方面,软件方面的问题是所使用的惯性传感器输出噪声大,需要对传感器的原始输出进行滤波处理,并使用控制理论方法加以控制,才能给控制器提供可靠的性能,并且防止阶跃扰动。而硬件方面的问题是微控制器运行控制算法所需的计算时间。过量的计算延迟导致倒立摆倾斜角的修正时间较长,使系统偏离垂直平衡位置。与传统的机器人相比,在自动平衡机器人的情况下,驱动电机保持平衡位置所需的功率要高数倍。
1.2 解决方案
在软件方面,为了滤除惯性传感器的噪声输出,需要使用滤波算法融合加速度计和陀螺仪的输出,以提供可靠的倾斜角度信息。目前常见的滤波算法有卡尔曼滤波、互补滤波、粒子滤波等。良好的数字控制算法可以提供最佳控制比例积分微分(proportion integration differentiation,PID)和线性二次调节器(LQR)。其他研究工作也探索了线性-高斯控制(LQG),模糊逻辑和极点配置方法的使用。
1.2.1 PID控制器
PID控制器是一种控制回路反馈,广泛用于工业和需要连续调节的控制系统。控制器连续计算系统的误差值e(t),并通过比例、积分和微分项调节控制输入量u(t),以使其随时间变化将误差降到最小。在数学上,其控制函数可表示为
(1)
式(1)中:u(t)为控制器的输出;Kp、Ki、Kd分别为非负比例、积分和微分系数。
1.2.2 LQR控制器
LQR控制集中于线性系统或线性化非线性系统以及成本函数的选择其中成本函数是状态和控制的二次函数。
通常情况下,线性系统线性系统由其状态空间表达式给出,其中包括矩阵A、B和C,表达式为
(2)
寻找一个使成本函数J最小的控制函数u,即
(3)
式(3)中:Q为正定(或正半正定)对称矩阵;R为正定对称矩阵。两个成本矩阵Q和R被称为权重矩阵,以便在称重状态向量需要每个相应元件有多快达到其所需的最终值引入。
利用代数黎卡提方程计算增益并最小化成本函数,则有
(4)
式(4)中:K为增益矩阵;P为轴心的位置。
在硬件方面,芯片技术的飞速发展为微控制器提供了更通用、更高效、更便宜和更可靠的选择。例如Arduino就是一款性能强、功耗低和成本低的开发板,滤波算法和控制算法都可以在Arduino中轻松实现。同时,配备高扭矩直流电机可以将机器人驱动至其垂直平衡位置并平衡整个物理结构。此外跟踪速度也是至关重要的,因为速度信息在车轮编码器的反馈回路中反馈给微控制器,以最大限度地减少误差以达到平衡。
2 两轮自平衡机器人数学模型
2.1 运动原理
通常而言,自平衡机器人平台由两个轮子连接在一个带有马达的车轴上。从车轴起,平台将垂直延伸以能够保持平衡。当平台倾斜时,其上的力不再与车轴垂直方向对齐,在平台的质心周围产生一个力矩。因此,必须有一个扶正的时刻,防止机器人翻倒。电机将在车轮上施加力矩并在平台上施加相等且相反的力矩。这种机制允许平台在倾斜时保持垂直。如果平台向前倾斜,那么轮子就会向前移动以保持它的直立。驱动车轮前进的时刻在平台上产生了一个向后的力矩,从而使它恢复平衡。
2.2 两轮自平衡机器人系统模型建立
系统数学模型建立是为物理结构设备形成一套有效控制策略的重要前提。为了推导两轮自平衡机器人的数学模型,将车身建模为质量集中于重心且旋转轴高于车轮轴的倒立摆,它将机器人限制为其功能的基本要素,以便将系统缩减为更简单的形式,可以更轻松地处理而不会损失实际系统的准确性。在该系统中,机器人的电机驱动车轮从原点行进时的移动距离与车轮的角加速度直接相关,同时,期望在运动过程中车体保持角度为0 rad。因此,两轮自平衡机器人的数学模型可以分为直流电机线性模型、车轮模型和摆体模型3个部分,最终得到系统的状态空间模型。如图2所示为两轮自平衡机器人平面模型。通常认为两轮自平衡机器人属于倒立摆的范畴,因此在进行物理建模时,常采用类似倒立摆的模型,其平面模型与倒立摆平面模型不同的是,两轮自平衡机器人还需要加以分析轮子的运动模型。
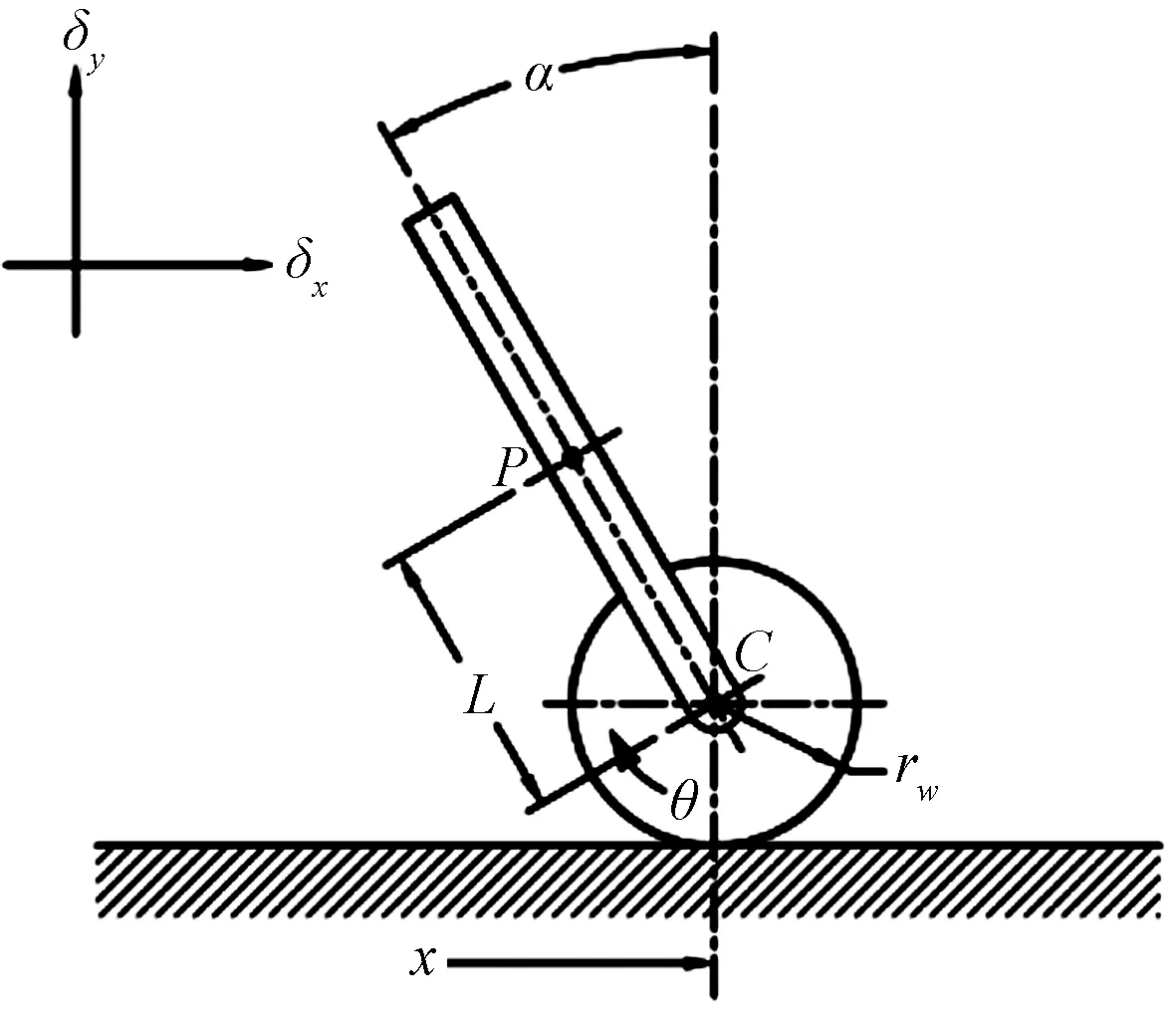
α为摆角;C为车轴位置;θ为车轮旋转角度;L为车体轴心到车轴之间的距离;rw为车轮半径
2.2.1 直流电机线性模型
机器人使用两个直流电动机来驱动车轮,电动机的电气等效模型如图3所示。
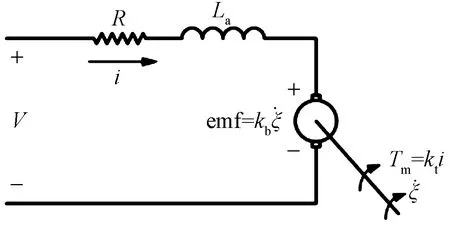
V为电机电压;R为电机电阻;La为衔铁电感;i为衔铁电流;kb为电机反电动势常数;emf为反电动势;kt为电机转矩系数;Tm为电机扭矩;ξ为电机相对于定子的旋转速度
电机模型需要将施加的电压与传递的扭矩相关联。该模型可以通过将电压与电流关联得到相关表达式为
(5)
电流与扭矩的关系为
(6)
式(6)中:Im为电机转子惯量;bm为电机转子的黏滞阻力。
假设电气系统响应比机械响应快得多,则电感可以忽略。此外,电刷电压和黏滞摩擦也都可以忽略不计。结合式(5)、式(6),并注意到电枢旋转角度是机器人主体角度α与车轮旋转角度θ之差,扭矩可以表示为
(7)
2.2.2 车轮模型
电机驱动车轮,车轮将机器人连接到地面。图4为车轮的平面运动模型。

Fp为摆体在车轮上的作用力;Fs为车轮与地面之间的反作用力;F为电机轴上的水平力;mw为车轮的质量;rw为车轮半径;Tm为电机扭矩;Tf为与电机角速度成比例的摩擦转矩
对绕车轮轴的扭矩求和以得出运动的旋转方程,得
(8)
式(8)中:Icm,w为车轮质心的惯性矩。
式(8)可与电动机转矩表达式组合以消除变量,得
(9)
车轮的运动平移方程为
(10)
2.2.3 摆体模型
针对水平方向,绕机器人质心的旋转以及垂直于摆的运动,得出了图5所示的机器人主体的运动方程为
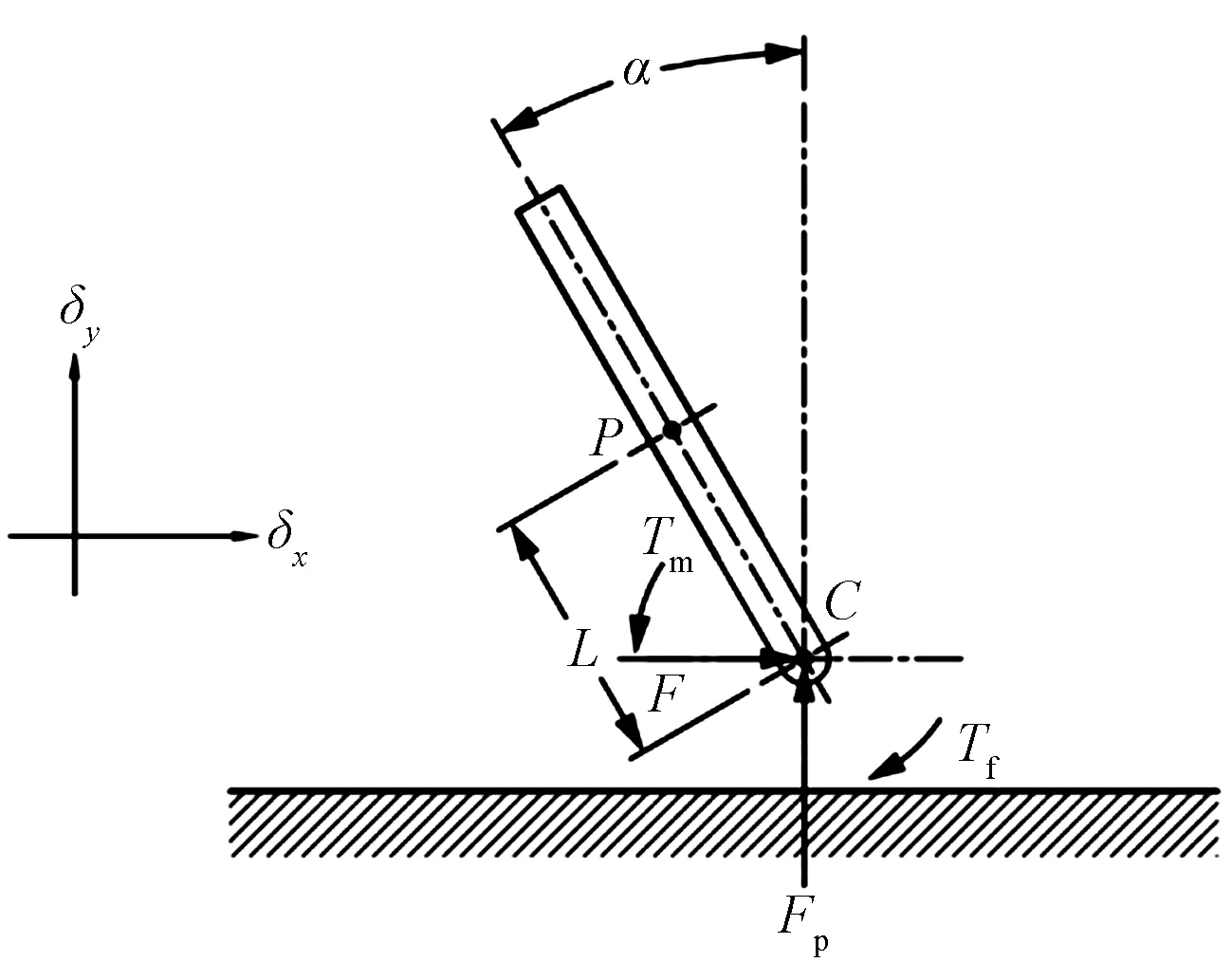
P为摆体参考点;α为摆体与垂直方向的俯仰角;L为车轮中心到P点的距离;mp为摆体质量;Ip为P点的惯性矩;x为车轮的水平位移;C为车轮中心位置
(11)
(12)
(13)
假设车轮不打滑,x=rwθ,并且等价于电机轴上的力,可以将式(7)、式(12)和式(13)组合在一起,以消除电机轴上的水平力,得

(14)
上述方程式中具有非线性项。因此,使用小角度假设将系统围绕所需的平衡点(摆角,α=0)进行线性化[其中sinα≈α,cosα≈1],可得

(15)
最终多项公式整理可得
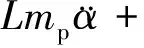
(16)
2.2.4 状态空间模型
得到系统的线性化方程后需要将其转换为状态空间形式。对于物理设备机器人而言,系统的状态变量x、系统输入u和系统输出y的定义为
(17)
使用模型中的线性化方程,可以将该模型的状态空间表示为
A=
(18)
(19)
(20)
式中:
(21)
测量单个机器人的参数与模型推导分析同样重要,系统模型中机器人的质量、摆的惯性常量等都会影响系统的稳定性和控制器的控制效果。因此,经过多次仿真测试与实体机器人测试,得到机器人的测量参数,如表1所示。

表1 两轮自平衡机器人测量参数
3 系统控制器设计与仿真分析
闭环系统也称为反馈系统,其使用系统之前的状态及其模型来计算系统的输入。这种类型的系统会检查其输出是否达到结果,是否存在任何错误。同时,该系统可以纠正错误,并且可以容忍系统中发生的任何干扰。对于两轮自平衡机器人而言,其控制器效率将通过垂直平衡、位置控制和干扰抑制能力进行测试。
3.1 系统稳定性分析
对于稳定系统,可以利用能控能观判别条件检查系统的可控性和可观察性。根据系统线性化空间状态方程的A、B、C和D矩阵,其中D为四行一列的0矩阵,并使用MATLAB对系统的可控性和可观性进行判断,如图6所示。

图6 系统能控能观性判断结果
从系统的可控制性矩阵和可观察性矩阵中发现两种矩阵的秩为4,即都是满秩的。因此,该系统既可控制,又可观察。
3.2 控制器设计
3.2.1 状态估计
使用摆的状态空间模型中的A和C矩阵找到闭环状态估计器。估计器的A矩阵计算公式为
Aest=Asys-LCsys
(22)
式(22)中:L为估计器内的反馈增益矩阵。
放置系统极点可以使系统稳定,并通过将极点远离y轴放置在S平面的左半部分,从而找到增益L以使系统比原有系统速度快5~6倍。
利用系统状态空间的A、B、C和D矩阵解得系统极点分布图,如图7所示。
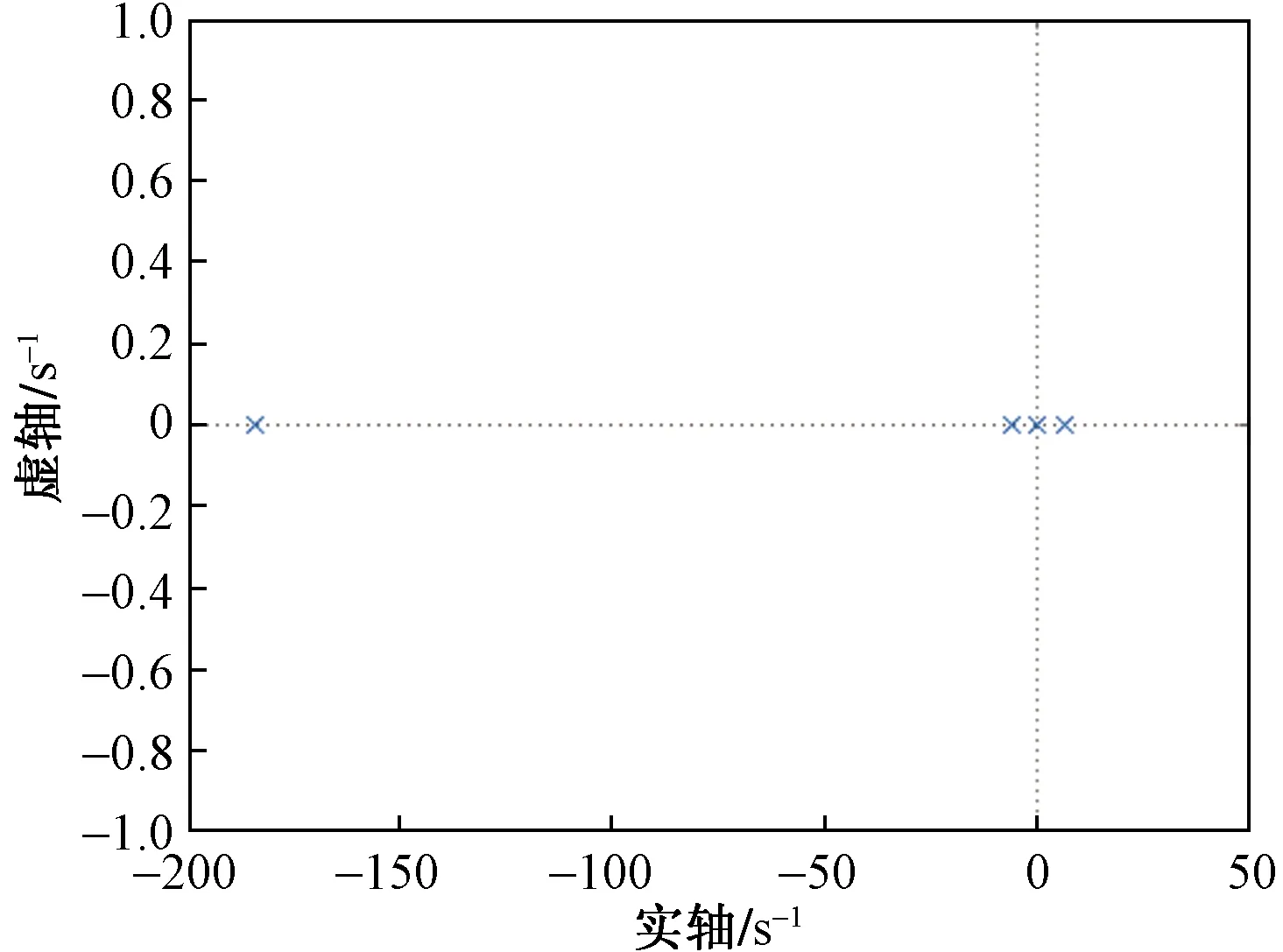
图7 系统极点分布图
将系统极点重新放置在S平面左半部分,并代入估计器,得到系统输出,如图8所示。
从图8可以看出,估计器状态虽然完全遵循原始系统状态,但是状态从x轴向无穷大发散,因此系统仍然不稳定。
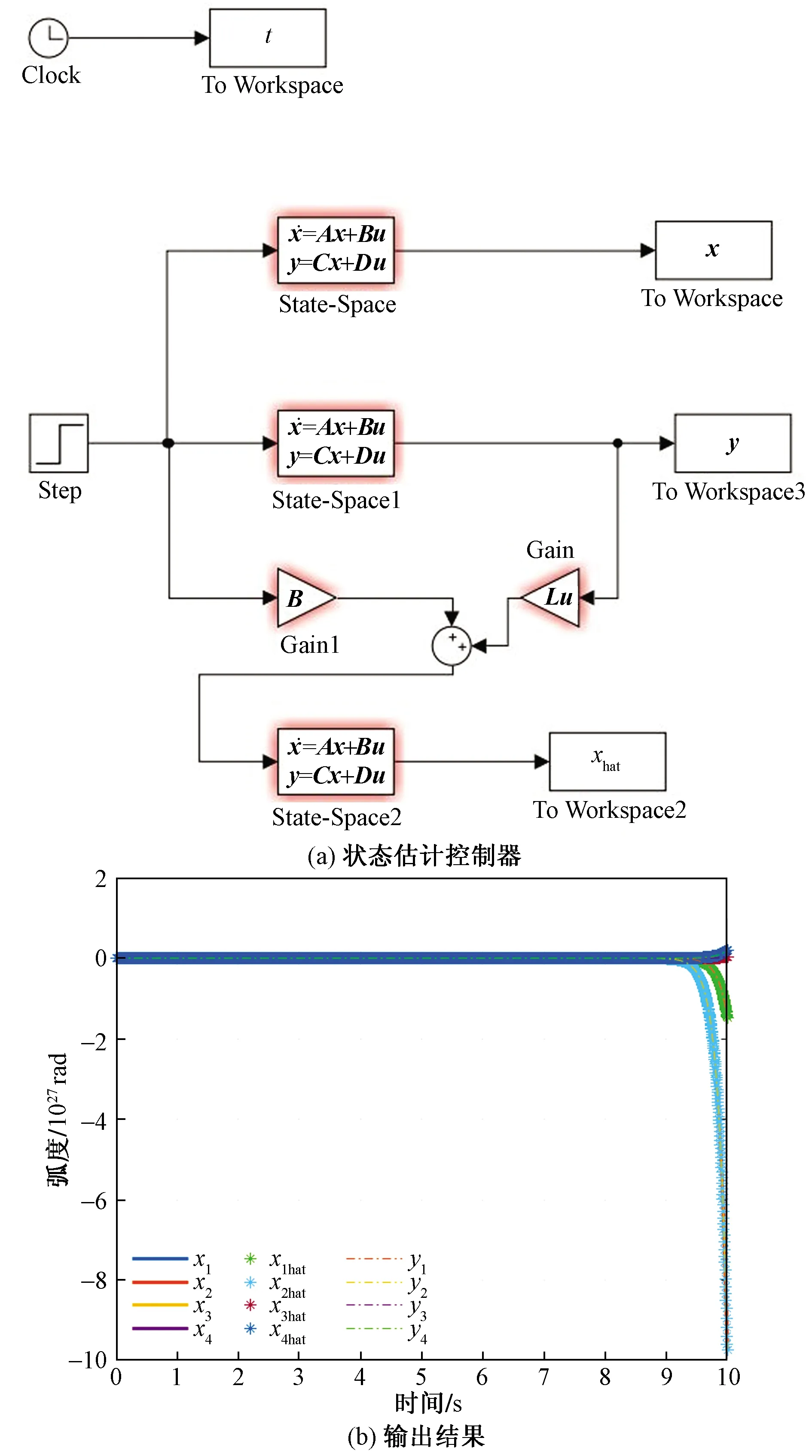
图8 状态估计控制器与输出结果
3.2.2 反馈控制
系统估计器已经完美跟踪状态。现在需要通过设计反馈控制器来使系统稳定。新的A矩阵可以表示为
Actr=Asys-BsysK
利用状态估计获得的增益L,可以得到系统的极点为[-67.2,-59.2,-12,-6],如图9所示。

图9 重新配置后的系统极点分布
将极点放置在[-67.2,-59.2,-12,-6]上,并通过在MATLAB中使用place命令找到了最佳增益K。将增益K代入到反馈控制器中,得到系统的输出如图10所示。
从图10可以看出,系统输出最初变化很大,但最终稳定到零。现在已限制输出,并且系统已稳定。

图10 反馈控制器与输出结果
3.2.3 具有状态估计的反馈控制
根据状态估计和反馈控制的效果,可以确定设计具有状态估计的反馈控制器会形成一个完整的稳定系统,如图11所示。
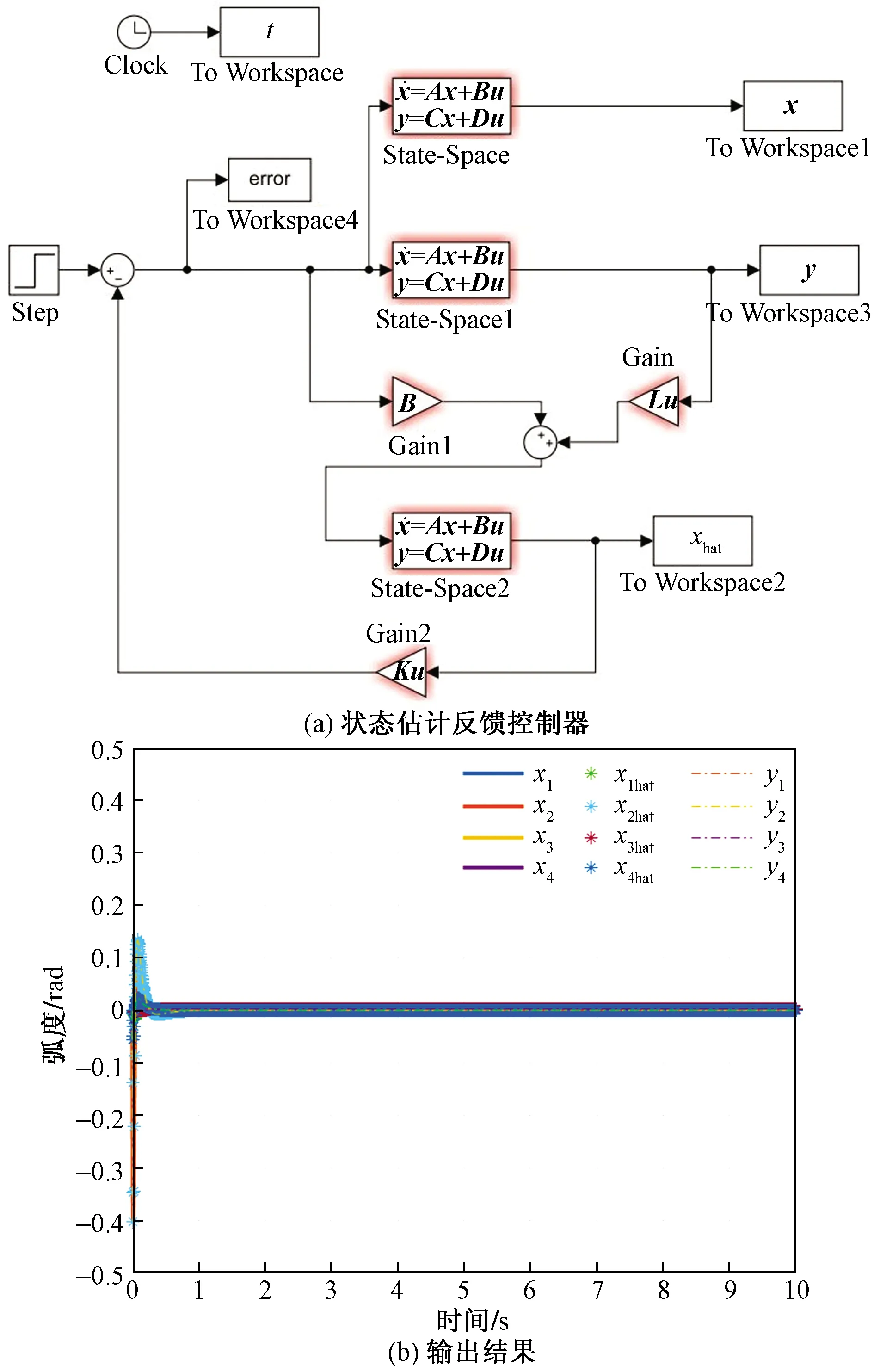
图11 状态估计反馈控制器与输出结果
从图11可以看出,系统起初的误差较大,但是随着时间的增加而逐渐降低。此外,系统在状态有界时变得稳定,并且稳定到零,同时估计器状态完全遵循原始系统的状态。
3.3 仿真实验与结果分析
根据设计好的具有状态估计的反馈控制器虽然可以保证系统稳定,达到较好的控制效果,但初始条件下的误差较大,对于实际的两轮自平衡机器人而言,很容易出现起摆失败甚至跌倒的情况。因此,在最终的系统仿真中利用两轮自平衡机器人的实际物理数据进行模拟仿真,同时引入LQR控制方法以期望取得更好的控制效果和控制成本。
从式(4)中可以知道除了Q和R以外的其余参数均为已知的,其中Q与控制器精度有关,R与控制器工作量有关。通常情况下,Q矩阵都是根据实际经验估计得到,需要依照实际控制效果进行修改。
经过多次仿真后,确定矩阵Q和R为
利用式(4)使用MATLAB求解方程,可以得到控制器的极点位置和增益。而有了这些参数,机器人就可以保持平衡运动。利用MATLAB设计两轮自平衡机器人运动动画界面,其中可以看到机器人在10 s内的运动位置,摆体的旋转角度以及摆体与垂直方向的状态对比,如图12所示。
从图12可以看出,机器人在运动过程中的整个运动状态分为加速、匀速、减速和保持平衡4个状态。此外,机器人刚启动时向前的加速度较大,摆体向前倾斜以平衡向后的反作用力,因此机器人摆体与垂直方向的角度偏差较大;当机器人运动到0.3 m处时,机器人从匀速状态逐渐进入减速状态,此时机器人加速度为负,从而导致机器人摆体稍微向后倾斜;当机器人接近并到达0.5 m处时,机器人进入保持平衡状态,机器人摆体与垂直方向基本重合,偏差为-4.778×10-6rad。

图12 两轮自平衡机器人运动动画
系统的响应速度与稳定性分析结果如图13所示。从图13可以看出,机器人在0~0.5 s的运行过程中摆体与垂直方向的角度偏差最大(约为 0.1 rad),而且机器人启动时的状态类似于倒立摆起摆状态(先向负方向回摆,后向正方向加速),机器人进入加速阶段;机器人在1~1.5 s的运行过程中摆体角度逐渐减小,位移曲线的斜率基本不变,说明机器人进入匀速阶段;机器人在1.5~4.5 s的运行过程中,摆体角度逐渐趋于0 rad,位移曲线斜率变小,说明机器人进入减速阶段;4.5~10 s的运行过程中,摆体角度基本保持在0 rad,位移基本保持在0.5 m,说明机器人进入保持平衡阶段。此外,可以看出加入LQR控制方法可以有效地降低机器人启动时的系统误差,虽然延长了系统的稳定时间,但是可以避免出现摆体倾角过大而可能出现起摆失败甚至跌到的情况。

图13 阶跃响应下LQR优化控制器的摆体角度与运动位移的输出图
4 结论与展望
两轮自平衡机器人的核心是必须能够在两个车轮上保持平衡,否则机器人的所有其他功能都会崩溃。根据直流电机线性模型、车轮模型和摆体模型推导出两轮自平衡机器人的运动控制数学模型并利用系统能控和能观性判断条件确定了系统具有能控和能观性。但是由于某些特征值位于S平面的右半部分,因此系统是不稳定的。为了得到一套完整的稳定系统,结合状态估计和反馈控制设计状态估计反馈控制器并引入LQR控制方法优化控制器性能。系统仿真实验结果表明,所设计的控制器对于移动机器人的平衡移动具有良好的控制效果。
系统具有完整的数学模型,因此,系统可以用作测试控制器的基准,对各种控制器的性能进行比较研究,例如,以设计非线性控制器并可以测试其性能,还可以定量地研究线性控制系统在实际非线性系统上的稳定性分析。
进一步的工作将通过添加视觉系统来提高机器人的自主水平,从而使机器人能够避开障碍物。此外,通过改进机器人的组件,希望获得更高的速度。另一个可能的扩展是将Arduino系统与其他传感器相结合,例如超声波和红外感应、GPS、数字罗盘和相机,以解决其他高级应用程序,例如避障和周边追随。
