基于改进非支配排序遗传算法的配电网动态重构

2021-08-20张照垄

科学技术与工程 2021年21期

张照垄，何莉，吴霜

(1.湖北工业大学电气与电子工程学院，武汉 430068；2.深圳大学机电与控制工程学院，深圳 518060)

在一次能源日益紧张、节能减排问题愈发严重的背景下，分布式电源作为一次能源的替代品，因其具备经济性、环保性等特点而被大力推广。当前，风能、太阳能等分布式电源的发电容量逐年递增，在配电网中渗透率也进一步增加。同时，分布式电源的随机性对电网运行的可靠性和经济性提出了重大的挑战。

配电网重构策略通过改变网络拓扑结构实现降低系统有功网损、增强系统安全性等目的[1-4]。在数学上，配电网重构是一个混合整数、非线性和非凸优化问题。因此，基于梯度的传统优化算法并不适合求解配电网重构问题[5]。因此，许多研究人员采用智能优化算法来解决配电网重构问题。文献[6]以提高系统的暂态稳定性、降低运行成本和功率损耗为目标建立模型，采用增强引力搜索算法求解配电网重构问题。文献[7]以系统有功网损为目标建立模型，并提出了一种基于粒子群优化算法和内德尔-梅德单纯形搜索算法的混合进化算法对模型进行求解。文献[8]通过使用最优潮流来同时获得最佳的规模、位置和网络拓扑结构，以最大限度地降低系统运行成本和功率损耗。文献[9]提出了一种考虑多时段负荷变化和开关操作次数等问题，以减少变压器出口侧三相电流的总体不平衡度和最小化开关操作次数为目标构建优化模型，并采用改进的微分进化算法对模型进行求解。

在求解过程中，处理多目标问题的常见方法是权重法，即将预定的权重因子分配给每个目标的加权方法。权重因子是通过计算或对某些目标的预期结果做出判断得出的[10-12]。然而，加权的方法只能得到一个帕累托解和一组权重因子的组合，显然不如可以得到一组帕累托解集的多目标算法。此外，配电网重构问题是一个约束优化问题，需要适当的约束处理技术来满足某些系统参数的定义限制。目前，罚函数法是常见的约束处理方法，这种方法的性能很大程度取决于惩罚系数的选择，不合适的惩罚系数往往会导致早熟现象的产生[13-14]。可见，适当的约束处理技术可以有效地减轻惩罚系数的选择负担。当用其兼容进化算法时，约束处理技术将搜索过程引导到可行区域，并有助于划分不可行区域和可行区域之间的边界。文献[15-16]成功地将基于可行解的优越性的约束处理技术应用在多目标最优潮流的研究中。文献[17]提出了基于ε-约束方法的多目标最优潮流模型。

目前，配电网重构策略中，主要是以网络损耗最小的单目标问题，或者结合电能质量如电压偏移、频率波动等最小为目标形成的多目标问题，而在电网重构策略中，考虑系统稳定性，同时降低系统运行成本还值得进一步研究。现建立以系统运行成本以及电压偏移最小为目标的配电网动态重构优化模型，并采用改进的非支配排序遗传算法(non-dominated sorting genetic algorithms Ⅱ，NSGA-Ⅱ)对模型进行求解。最后，采用IEEE 33节点系统进行算例分析，验证文中模型和算法的有效性。

1 配电网动态重构的数学模型

配电网动态重构属于非凸非线性优化问题，其在满足一定的约束条件下，使得电网中的某些目标达到最小化[18]。配电网动态重构问题通常考虑分布式电源处理和开关工作状态作为决策变量。然而，在实际的电力系统中，无功补偿装置和有载调压变压器也常常作为调节配电网潮流的手段。因此，在传统模型的基础上将变压器分接头挡位以及静态无功补偿装置考虑为决策变量。

1.1 目标函数

以系统运行成本和电压偏移最小为目标建立配电网动态重构模型。

(1)系统运行成本最小。

(1)

式(1)中：Closs,t为网络损耗成本；Cs,t为网络重构成本；CDGcut,t为弃风弃光成本。

Closs,t=λlossPloss,t

(2)

式(2)中：λloss为网络损耗的单价；Ploss,t为t时间内的网络损耗。

Cs,t=λs|Sk,t-S0,k,t|

(3)

式(3)中：λs为开关操作费用；Sk,t为第k个开关在t时间的运行状态；S0,k,t为第k个开关在t时间的初始状态。

CDGcut,t=CWP,cut+CPV,cut

(4)

(5)

(6)

式(4)中：λWP,cut、λPV,cut分别为弃风、弃光成本；PWP,i,max、PPV,i,max为第i个电源的预测弃风、弃光出力；PWP,i、PPV,i为第i个电源的弃风、弃光实际出力。

(2)电压偏移最小。在配电网中，衡量电压质量的指标是电压偏移，这一指标对系统稳定运行具有重要意义。该指标被定义为配电网中各个节点电压偏移的累积值。

(5)

式(5)中：Vi为节点i的电压；Ve为节点i的电压的期望值(通常为1 pu，pu为标幺值单位)。

1.2 约束条件

(1)潮流约束。

(6)

式(6)中：Pi,L和Qi,L分别为i节点的有功和无功负荷；Vi、Vj分别为节点i和j处的电压;Ωi为与节点i相连的其他节点集合；Gij、Bij分别为支路i和j之间的电导和电纳；θij为节点i和j之间的相角差。

(2)节点电压约束。

(7)

(3)电流约束。

(8)

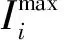
(4)分布式电源出力约束。

(9)

(5)变压器约束。

(10)

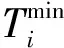
(6)辐射状电网约束。

gn∈GN

(11)

式(11)中：gn为当前的网络结构；GN为所有允许的辐射状网络结构，即网络呈辐射状，不存在环网。

2 改进NSGA-Ⅱ

配电网重构问题属于多约束多变量问题，对算法性能要求更高，在NSGA-Ⅱ的基础上进行了改进，即基于可行解优越性的约束处理方法和采用算术交叉算子增强算法的全局搜索能力。

2.1 算术交叉算子

NSGA-II的交叉过程中一般采用二进制交叉算子，其表达式为

(12)

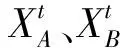
(13)

式(13)中：Xrank为X个体在非支配排序中所在的非支配层数；Yrank同理。可以看出，由于Xrank和Yrank具有不确定性，因此α也具有随机性。随着算法的运行，种群中的个体逐渐接近帕累托前沿，α的波动范围也随之变小。因此，基于算术交叉算子的交叉过程不仅减少了算法的随机性，也具有较广泛搜索空间。

2.2 基于可行解优越性的约束处理方法

当使用进化算法求解约束优化问题时，必须采用有效的约束处理方法来有效地利用不可行解中存在的信息，以便引导算法向全局最优的方向进行搜索。

约束多目标问题的数学定义为

Minimize:F(x)=[f1(x),f2(x)，…,fm(x)]

(14)

s.t.gi(x)≤0,i=1,2，…,p

hj(x)≤0,j=1,2,…,q

(15)

式中：m为目标数；x为决策变量；gi(x)为不等式约束；hj(x)为等式约束；p、q分别为不等式约束和等式约束的数量。

首先，将等式约束转化为不等式约束，即

|hj(x)|-δ≤0,j=1,2,…,q

(16)

式(16)中：δ为正容差值。

然后对约束违反值做如下定义：

(17)

对约束进行归一化处理，对于同一组决策变量的总体违反约束情况可以表示为

(18)

式(18)中：ωi=1/Gi,max，Gi,max为违反约束的最大值；m为约束的数量。在进化计算过程中，ε(x)可以表示个体违反约束的情况，当ε(x)为0时即该个体完全满足约束。

判断解的优越性(以下情况认为xi优于xj)：

(1)xi为可行解，xj为不可行解。

(2)xi和xj都为可行解，但是目标值f(xi)小于f(xj)，即假设目标求最小值。

(3)xi和xj都为不可行解，但是ε(xi)小于ε(xj)。

上述判断中认为可行解优于不可行解，利用总体违反约束的情况来评价两个不可行解，从而让个体向着可行域进化。对于可行解，利用目标值衡量优劣。所以，该处理方法可以有效地提高解的质量。

2.3 基于模糊决策方法选择最佳方案

在求解动态重构的过程中，对每个时段都运行10次，并得到10组帕累托前沿。然后采用超体积(hypervolume, HV)指标作为衡量帕累托前沿优劣的标准，以此为依据选择最佳帕累托前沿。HV指标可以评估多目标进化算法产生的帕累托前沿中解的多样性和收敛性。在配电网重构的问题中，由于目标的取值范围不同，所以要对其进行归一化，即

(19)

式(19)中：Oi为进行归一化之后的目标值；Obji为归一化之前的目标值；Objmax和Objmin为目标的最大值和最小值。

对于具有M个目标的多目标优化，超体积指标计算中的参考点用(1,1,…,1)M来表示，并用一百万个蒙特卡洛采样点来寻找近似的HV指标。对于给定的问题，比较不同的帕累托前沿时，认为HV指标最大的帕累托前沿最佳。

采用模糊决策方法从帕累托解集中选择最佳方案。目标的隶属度函数可以表示为

(20)

(21)

式(21)中：N为非支配解的个数；M为目标个数。最佳方案选择uk值最大的非支配解。

2.4 算法合理性验证

反世代距离评价指标(inverted generational distance, IGD)指计算帕累托前沿上点到获取的种群的最小距离的平均值，通过量化多目标进化算法的收敛性和多样性来评价算法性能。该指标因其在解决高维多目标优化问题时所体现的优越性而被广泛采用[19]。因此，采用IGD指标来评价改进NSGA-II算法的综合性能。

IGD计算公式为

(22)

式(22)中：P为均匀分布在真实帕累托前沿上的点集；|P|为真实帕累托前沿上的点个数；Q为算法获取的帕累托最优解集。

ZDT3的测试函数表达式为

(23)

采用测试函数ZDT3对改进NSGA-II进行测试。其中，种群规模为100，最大迭代次数为200次，交叉概率为0.7，变异概率为0.02。将计算所得数据与原始数据进行对比[20]，10次运行平均值结果如表1所示。

表1 IGD指标对比结果

由表1可以看出，相比原始的NSGA-Ⅱ，改进NSGA-Ⅱ的IGD指标更小，说明改进NSGA-Ⅱ的收敛性和多样性更好。图1为改进NSGA-Ⅱ和NSGA-Ⅱ在测试函数ZDT3上所得的帕累托前沿与真实帕累托前沿的对比，可以看出，相比NSGA-Ⅱ，改进NSGA-Ⅱ所求的帕累托前沿与真实帕累托前沿重合度更高。结合以上分析，可知改进NSGA-Ⅱ能够得到更好的帕累托最优解。

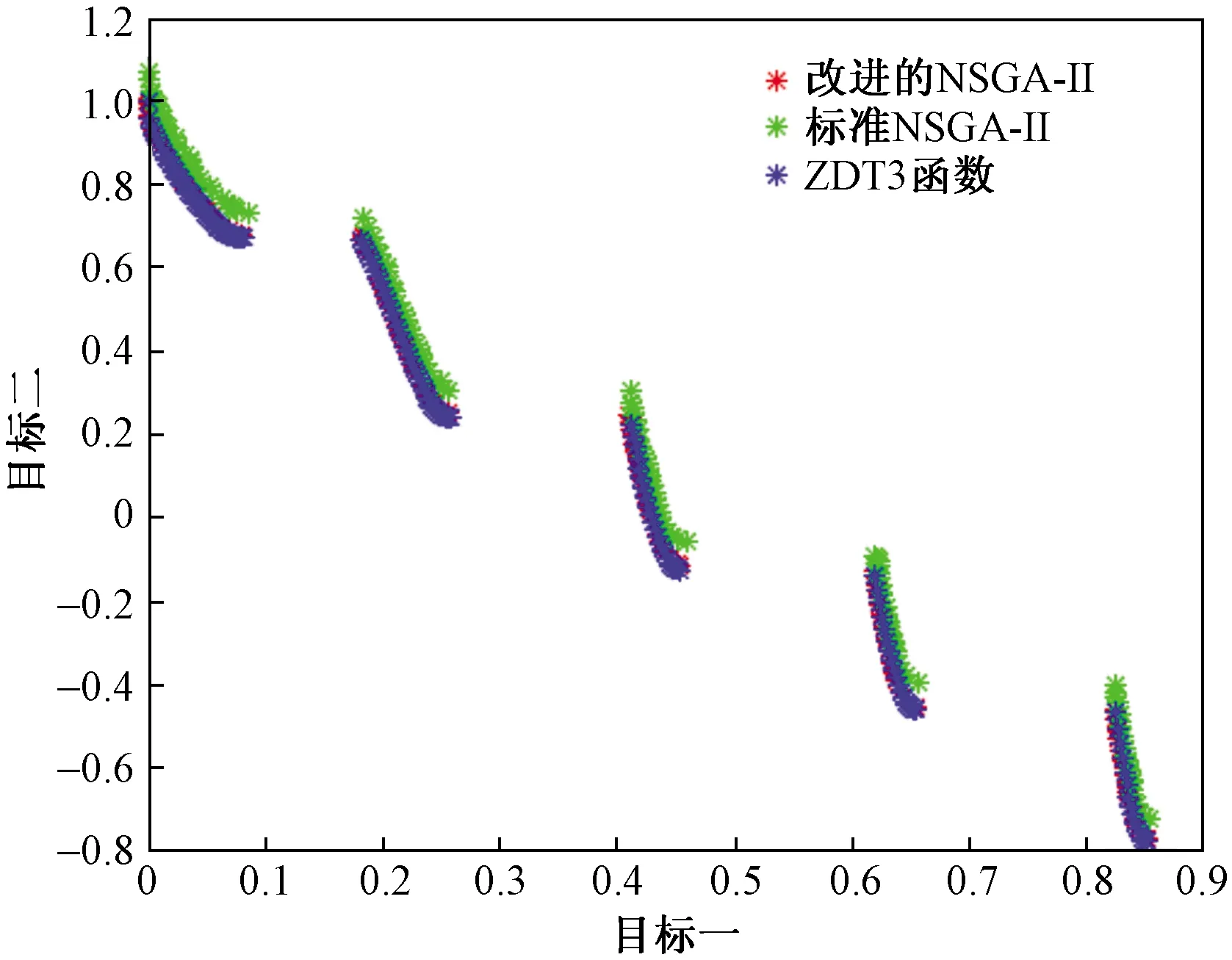
图1 改进NSGA-Ⅱ在ZDT3的帕累托解

2.5 改进的NSGA-II求解配电网动态重构模型

通过改进的NSGA-II对配电网动态重构模型进行求解，算法流程图如图2所示。

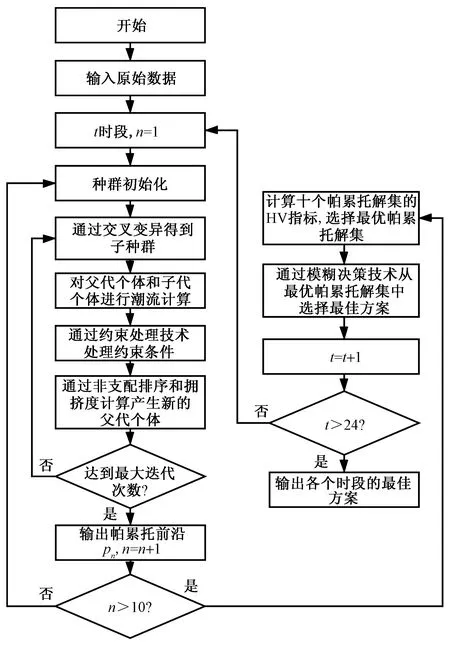
图2 算法流程图

求解步骤如下：

(1)算法参数初始化。

(2)通过交叉变异得到与原始种群同样规模的子种群。

(3)进行配电网重构和潮流计算，得到系统中的各项数据。

(4)采用约束处理技术对约束进行处理，并结合非支配排序和拥挤度计算在原始种群和子种群中选择出新种群。

(5)判断算法是否达到最大迭代次数，若满足则输出帕累托解集，否则返回步骤(2)开始新一轮的计算。

(6)采用模糊决策方法从帕累托解集中选择出最佳方案。

4 算例分析

4.1 基础数据

为验证本研究的有效性和合理性，在MATLAB的平台上编程实现。文中选取IEEE-33节点系统作为测试系统。分别在节点10、18和21接入风电，额定有功功率分别为600、1 100和1 000 kW。在节点7、16和33接入光伏，额定有功功率分别为500、900和1 100 kW。弃风弃光成本为1元/(kW·h)，网络损耗成本为5元/(kW·h)，开关操作成本为7元/次。NSGA-Ⅱ中，种群大小为100个，迭代次数为100次，变异概率为0.02，交叉概率为0.7。系统图如图3所示。

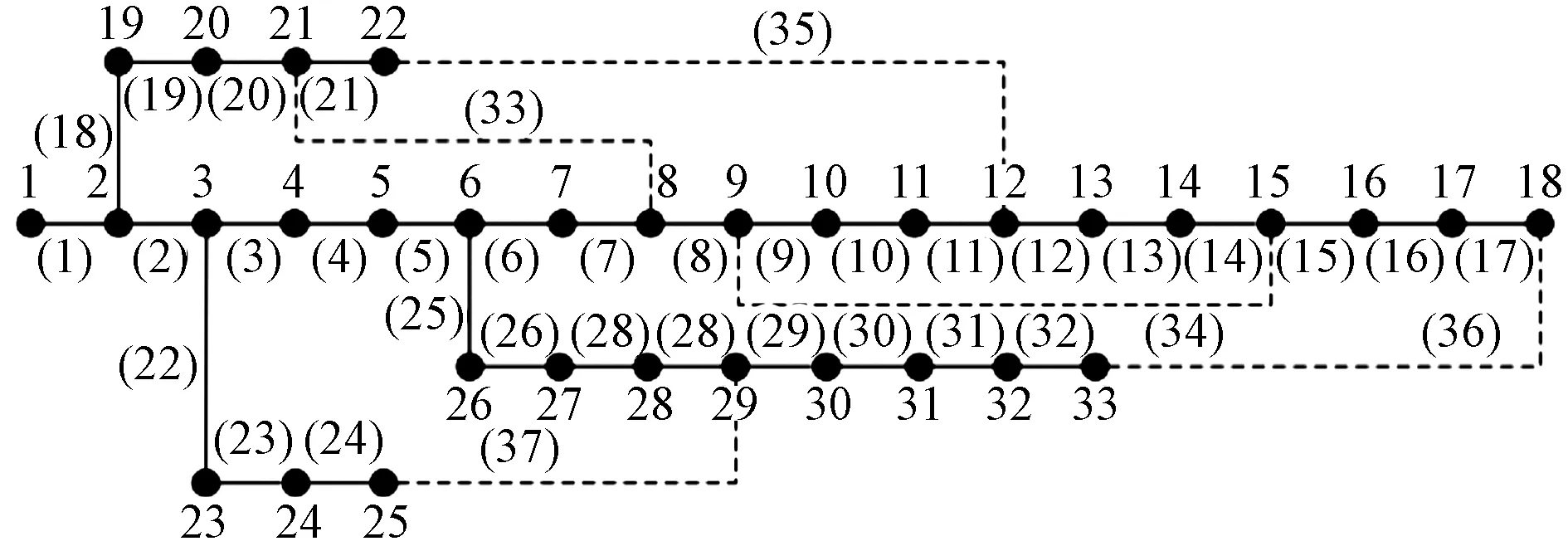
图3 IEEE-33节点系统图

4.2 模型对比分析

为证明模型的合理性，以IEEE 33节点系统为例，分析安装有载调压变压器和无功补偿装置对系统的影响。结果如图4所示。

图4中，Case1为原网络的电压分布情况，Case2为在原网络基础上安装有载调压变压器和无功补偿装置的电压分布情况。可以看出，原网络的电压波动很大，系统的最低电压出现在节点17，最低电压为0.910 8 pu远远低于满足系统稳定要求的电压下限值。当安装有载调压变压器和无功补偿装置后，系统的电压波动明显减小，最低电压为0.981 9 pu，符合系统运行的稳定性要求。这也证明了安装有载调压变压器和无功补偿装置可以优化系统的电压分布。

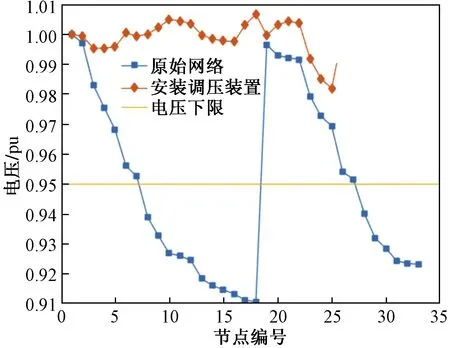
图4 电压分布情况

4.3 多目标与单目标优化对比分析

为验证算法的正确性，进行了单目标和多目标的对比分析，即分别以运行成本和电压偏移进行优化与运行成本和电压偏移的多目标进行优化的结果进行对比，如表2所示。

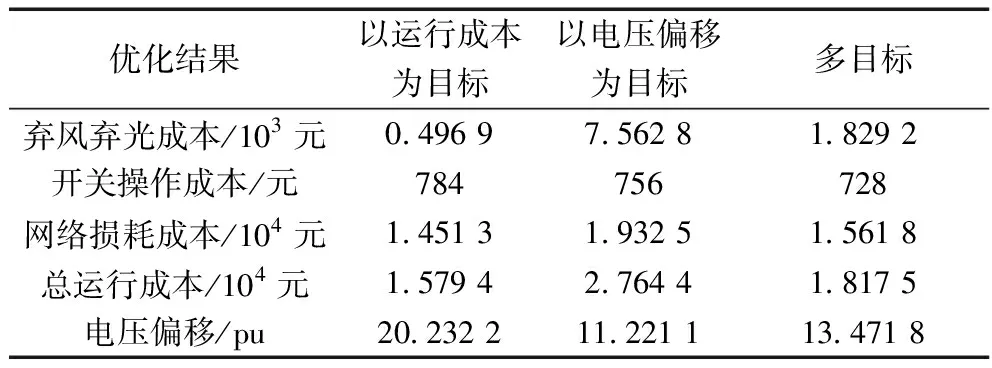
表2 单目标与多目标优化对比结果

由表2可以看出，相比以系统运行成本最小进行单目标优化，多目标优化以增加系统运行成本为代价，提升了系统的电压质量。同样，对比以电压偏移为目标进行单目标优化，多目标优化以降低系统电压质量为代价，降低了系统运行成本。这符合帕累托最优思想，验证了模型的正确性。

4.4 计算结果分析

通过上述方法以IEEE 33节点系统为例进行配电网动态重构。优化结果如表3所示。

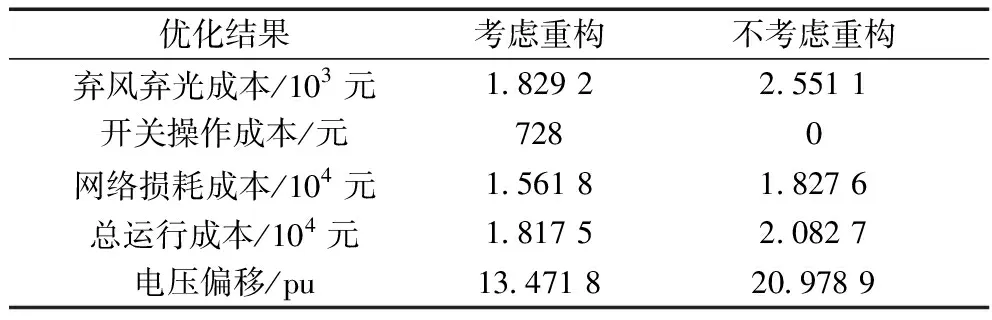
表3 优化结果

由表3可以看出，考虑网络重构时，弃风弃光成本为1.829 2×103元，网络损耗为成本为1.561 8×104元，开关操作成本为728元。当不考虑网络重构时，虽然开关操作成本为0元，但是弃风弃光成本增加了39.47%，网络损耗成本增加了17.02%，最终导致总运行成本增加了14.59%。这也表明了网络重构对降低系统运行成本具有明显的作用。同时，在考虑网络重构时，配电网的电压偏移为13.471 8 pu，不考虑重构时，配电网的电压偏移为20.978 9 pu，可以看出网络重构也有利于提高系统的电压稳定性。考虑重构时，各个时段的详细优化结果如表4所示。

表4显示了24个时间段内系统的电压偏移情况，可以看出在6:00—7:00时电压偏移最大。因此，选择6:00—7:00时3种情况下的电压分布进行对比分析。电压分布图如图5所示。

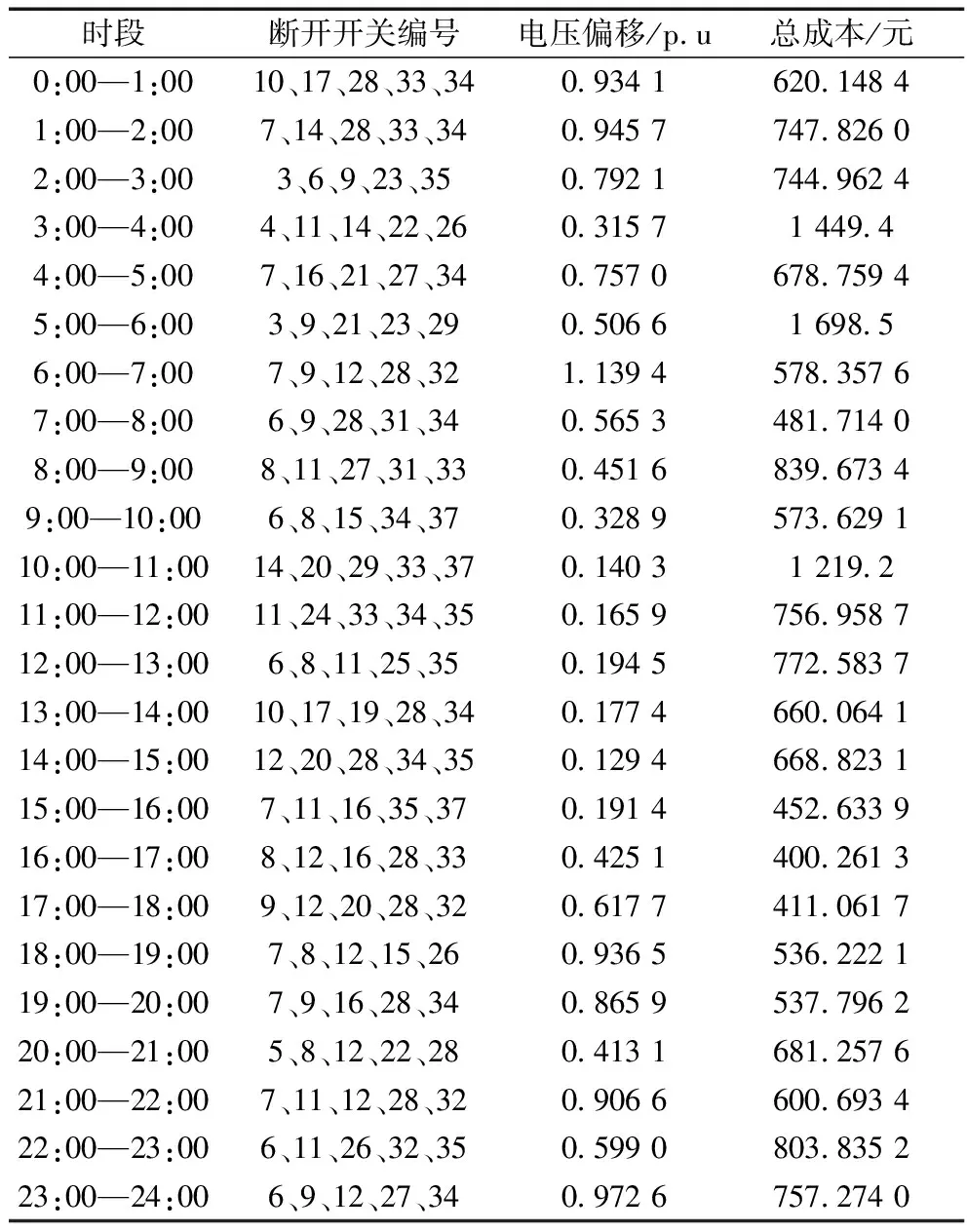
表4 网络动态重构结果

图5 6:00—7:00时各个节点的电压分布

由图5可以看出，原网络的电压波动很大，系统的最低电压出现在节点17，最低电压为0.910 8 pu远远低于满足系统稳定要求的电压下限值。当加入分布式电源之后，相比原来的网络，电压波动的幅度虽然有所改善，但是节点29、30、31、32和33的电压依然低于指定的下限值0.95 pu。当考虑网络重构时间，所有节点的电压均在0.95～1 pu的范围内，满足系统稳定的要求。同时，电压的波动也较以上两种情况小。