铝合金框架结构的弹体穿击损伤特性
2021-08-20蔡建纲谭剑锋于领军史瑞鹏夏云松
蔡建纲,谭剑锋*,于领军,史瑞鹏,夏云松
(1.南京工业大学机械与动力工程学院,南京 211816; 2.陆军航空兵学院航空机械工程系,北京 101123)
直升机因为具备灵活飞行特点,在现代局部战争中备受青睐[1]。但低空作战时机身框架易受子弹弹击导致损伤,而弹伤的可修复性评估是修复工作的前提,影响战场快速抢修的效率和价值,为此研究弹伤破坏程度和相关参数的影响规律尤其重要。
到现阶段为止,国外针对子弹侵彻的理论和实验已经开展了很多研究[2-3]。中国在弹击研究与国外相比较晚,起初主要的工作内容是研究简单结构碰撞变形的问题。肖玲等[4]、穆建春等[5]通过实验和数值计算研究了圆锥头弹体正面冲击薄壁金属圆板的变形破裂模式,并估算了圆板的临界破裂速度。穆建春等[5]在简单模型理论研究的基础上加入了多方面因素的影响,从单因素到多因素研究逐步被补充。王维占等[6]、Khaire等[7]、陈刚等[8]针对子弹型号、角度、速度等因素高速侵彻金属靶的问题进行了有限元模拟和实验,分析子弹对实验样板的冲击影响。近几年,随着复合材料的使用范围越来越广,人们对复合材料弹伤的研究也提上了日程。古兴瑾等[9]研究了不同弹体形状对复合材料靶板高速冲击损伤程度的影响。Liu等[10]数值模拟预测了弹丸冲击碳纤维增强热塑性复合材料时硬度的影响。此外,研究的靶板对象也开始从简单样板结构向复杂的实物结构转变。李晓彬等[11]选取了直升机旋翼桨叶作为研究对象,通过仿真计算的研究方式预测了桨叶的损伤范围。以上研究从不同角度研究了弹击问题,前期的研究内容较为全面,但多数针对规则矩形样板弹侵问题作研究,与实际结构损伤情况误差较大,针对复杂结构实物模型的弹伤研究还很欠缺。机身铝合金框架结构弹伤问题之前并没有过相关研究,而机身损伤问题的研究是战场快速修复技术发展的前提,故研究内容具备一定程度上的工程指导作用,具有重要的研究价值和意义。
为掌握铝合金结构子弹穿击损伤特性,进而为抢修奠定理论基础,现基于ABAQUS软件平台,采用修正后的Johnson-Cook模型[8],建立机身框架弹伤冲击的显示动力学模型,研究子弹弹头倾角和子弹材料等参数对机身铝合金框架的损伤影响。
1 计算方法
1.1 材料本构关系失效模型
子弹材料采用常见材料铜和钢,材料参数如表1所示。子弹的本构关系采用双线性硬化模型来描述[12],表达式为
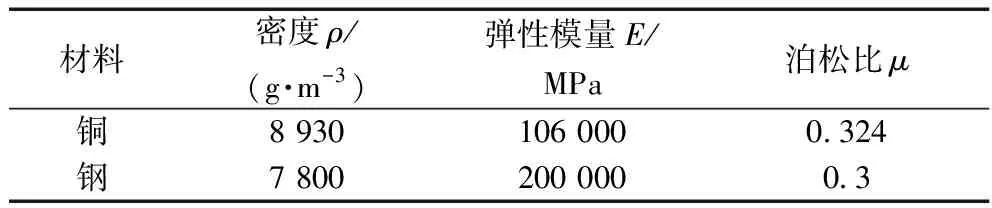
表1 子弹材料参数
(1)
式(1)中:σ为应力;E为弹性模量;Et为切线模量;σ0为屈服强度;ε0为初始屈曲时的应变。
以直升机铝合金2A50机身框架为研究对象,材料参数如表2所示。

表2 靶板材料参数及Johnson-Cook模型的失效参数(铝合金2A50)
针对子弹穿击问题,选用Johnson-Cook[9]损伤,表达式为
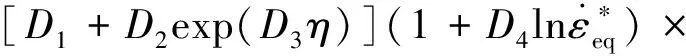
(1+D5T*)
(2)
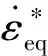
金属材料的延性断裂与材料的穿孔形状及变形拉伸收缩形式有关,这两个因素的表现形式通常取决于材料的应力状态。除此之外,温度和应变率等因素对金属的延性断裂也产生一定程度的影响[13-14]。
修正过的Johnson-Cook的损伤模型[15],表达式为
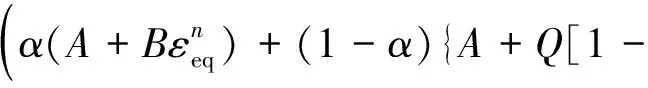
(3)
式(3)中:εeq为材料等效塑性应变;Q为当前温度下材料屈服强度;n为材料应变硬化系数;β为材料硬化指数;α为材料修正系数(0≤α≤1);C为材料应变率敏感系数;P为材料温度软化系数;M为材料温度软化指数。
Johnson-Cook失效模型中采用线性损伤演化模拟材料断裂的产生[16],表达式为
(4)
式(4)中:Δεeq为单位循环时间步的有效塑性应变增量。当上述D值到达1时,判定材料发生失效[17]。
1.2 机身框架弹伤冲击动力学模型
1.2.1 冲击动力学方程
连续介质的冲击动力学问题可通过5类基本方程描述,包括连续性方程公式、动量方程公式、几何方程公式、本构方程公式及能量方程公式。设初始Lagrange坐标为X=(X1,X2,X3),t时刻运动到新位置,Euler坐标为x=(x1,x2,x3),大写X表示初始构型,小写x表示现时构型。
连续性方程公式为
(5)
动量方程公式为
(6)
几何方程公式为
(7)
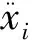
在数值模拟分析中,主要考虑应变率对应力应变关系的影响,如果材料已进入塑性阶段,采用Von Mises屈服条件,表达式为
(8)
一般冲击问题中忽略热传导的作用,单位体积的能量方程为
(10)
上述5个基本方程在一定的边界条件和初始条件下可用解析方法或数值方法求解。
1.2.2 三维模型与网格划分
数值仿真基于ABAQUS软件平台,计算分析子弹碰撞铝合金框架三维实物模型对框架结构产生的损伤影响。基于CATIA软件平台模型,如图1所示,由于弹伤中子弹受损较小,变形轻微,因此假设弹体为刚体,针对倾角和材料因素分析,选取弹径5.8 mm、弹长2.4 mm×10 mm,如图1所示。网格整体尺寸为0.5,网格类型选择Hex,划分方式选择Sweep,Element Library选择Explicit,Hourglass Control选择默认。

图1 子弹3D模型
框架模型同样通过CATIA软件平台建立,如图2所示。导入ABAQUS/CAE模块做后处理,网格尺寸为5,局部尺寸细化为0.5,网格类型设置考虑外形特征选择Hex-dominated,其他与子弹网格设置一致,Hourglass Control选择Relax stiffness。

图2 铝合金框架3D模型
1.2.3 求解方法
现阶段针对冲击动力学问题研究的数值模拟方法有任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian,ALE)法、Euler法及Lagrange法等,其中Lagrange描述增量法是目前这一领域最成熟、最简便、应用最广泛的有限元方法,常用于处理固体之间冲击动力学问题的分析。弹体侵彻问题符合上述情况,故选用该法作为求解方法。
1.3 冲击动力学模型验证
为验证模型的合理有效性,选取文献[9]中的实验数据做对比。参考实际弹击情况,选取常见数据作为研究参数[8],子弹模型选取弹径为5.8 mm,弹速为9.3×102m/s。仿真基于ABAQUS软件平台,建立直径为5.8 mm弹体和截面为150 mm×150 mm的矩形靶板,对靶板中心接触部分网格加密,网格总量为1.14×105,三维模型和网格划分结果如图3所示。仿真过程设置初始速度为 9.3×102m/s,弹体分别对厚度为1.5、3.0、4.5 mm的靶板进行高速垂直冲击数值模拟。

图3 实验验证三维模型图
子弹材料选用铜和钢,材料参数如表2所示,靶板材料选用结构钢。靶板的失效模型选用Johnson-Cook失效模型,针对撞击接触相互作用问题中切向行为的摩擦因素选用罚函数法,材料钢的基本参数和Johnson-Cook模型的失效参数如表3所示。

表3 靶板材料参数及Johnson-Cook模型的失效参数(钢)
通过实验和仿真计算给出了高速冲击后弹体的剩余速度数据对比,如表4所示。
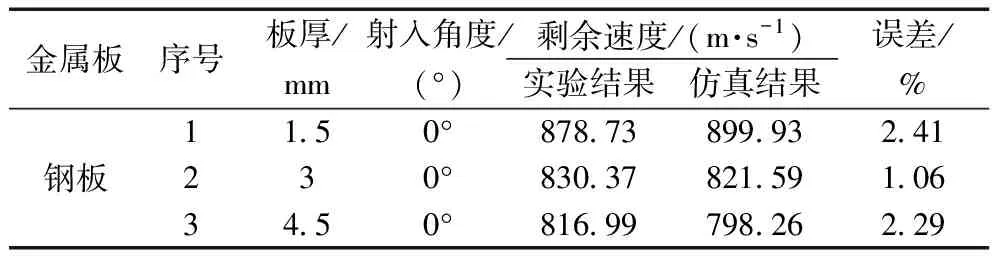
表4 子弹剩余速度实验和仿真数据对比表
对实验得到的数据和仿真得到的数据进行后处理,对比曲线如图4所示。

图4 不同板厚子弹穿击实验仿真数据对比图
不同板厚弹伤计算结果与实验测量结果趋势吻合较好,相对误差小于5%,由此表明所建立计算模型的准确性。
随着时间的增加,子弹剩余速度迅速减小,减小速率先增大后减小。随着厚度的增加,剩余速度减小速率也明显增大。
2 机身铝合金框架弹伤特性
为保证分析结果的合理性和适用性,针对倾角和材料两个方面建立多组模型进行对比。倾角θ分别为15°、30°、45°、60°、75°和90°,如图5所示,子弹分别为铜质子弹和钢质子弹。对比分析框架内部最大应力和子弹剩余速度。
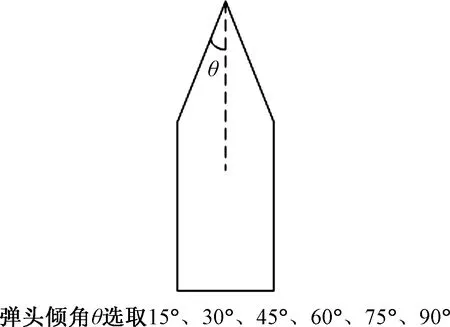
图5 子弹截面简化图
将上述模型导入ABAQUS/Explicit模块中计算,计算过程中由于子弹尺寸相对机身框架尺寸较小,出现细化网格量过大,计算周期过长等问题。由云图可知子弹对距离冲击部位较远结构的应力应变影响较小,可以忽略不计,故为方便网格细化,缩短计算时长,试截取撞击部位局部结构做细化分析,网格数量在1.79×106~2.22×106,局部结构模型和网格划分结果如图6所示。

图6 机身铝合金框架局部三维模型网格划分结果图
整体和局部计算云图如图7所示,并作整体局部分析子弹剩余速度随时间变化对比曲线图,如图8所示。
图7和图8表明,整体计算结果和局部计算内部最大应力分别为5.105×102MPa和5.296×102MPa,子弹剩余速度分别为8.513×102m/s和8.524×102m/s,结果趋势吻合较好,相对误差小于0.15%。误差原因主要是局部计算网格细化导致计算精度提高,从安全裕度的角度考虑局部计算结果更有参考价值,故后面计算均采用局部结构进行计算。
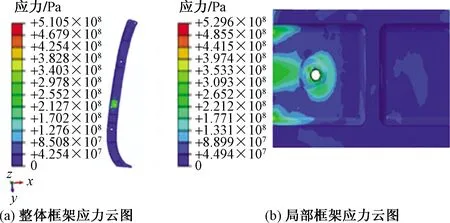
图7 整体和局部框架应力云图
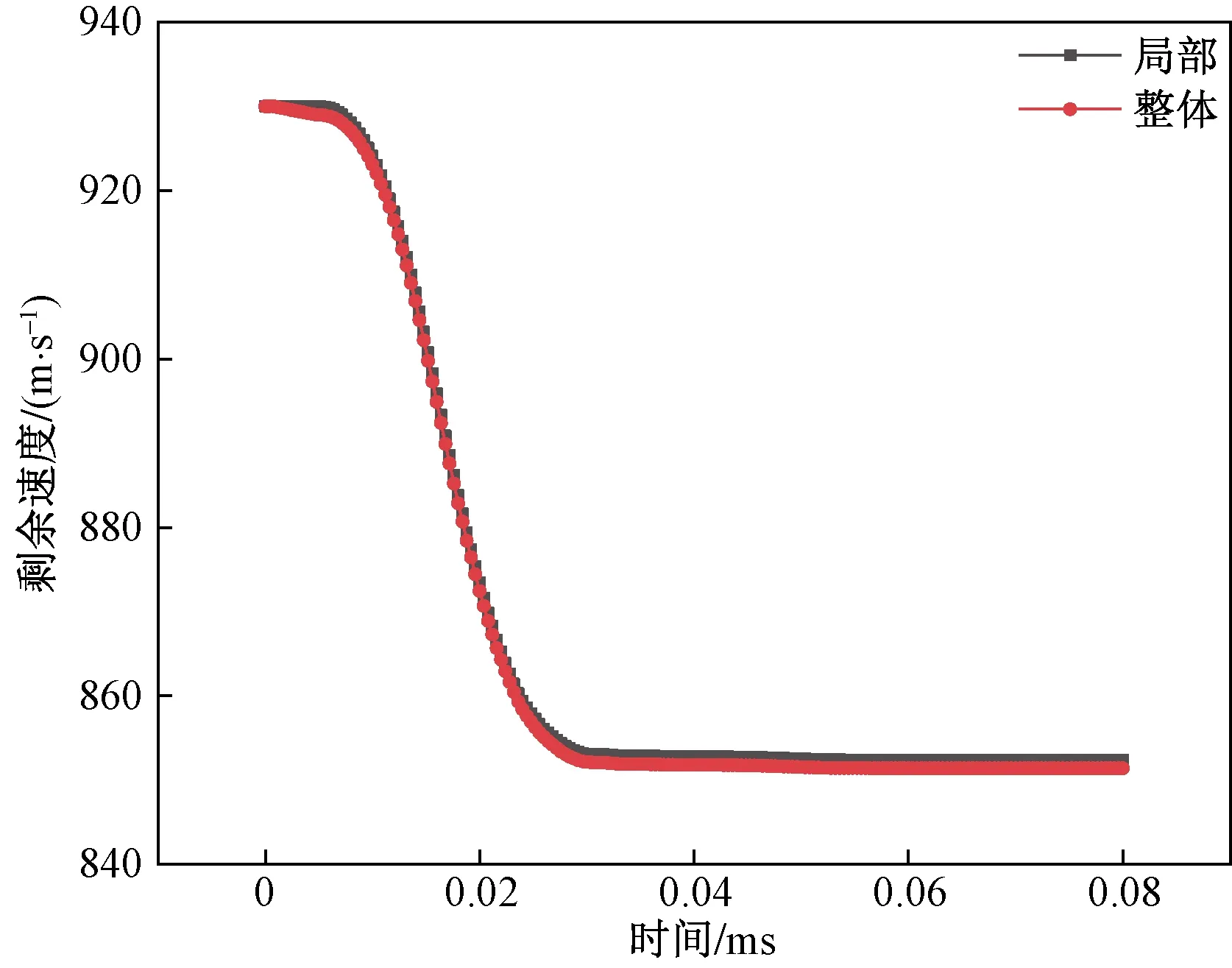
图8 子弹剩余速度对比图
3 子弹参数对机身框架弹伤影响
3.1 子弹弹头倾角对机身铝合金框架的弹伤影响
为了方便分析弹头倾角的影响,统一选取计算参数弹径为5.8 mm,对应弹速为9.3×102m/s,子弹为铜质子弹。倾角θ选取6个角度计算撞击结果(即子弹轴线与弹头表面成15°、30°、45°、60°、75°和90°)。对应角度的撞击结果的应力云图如图9所示。
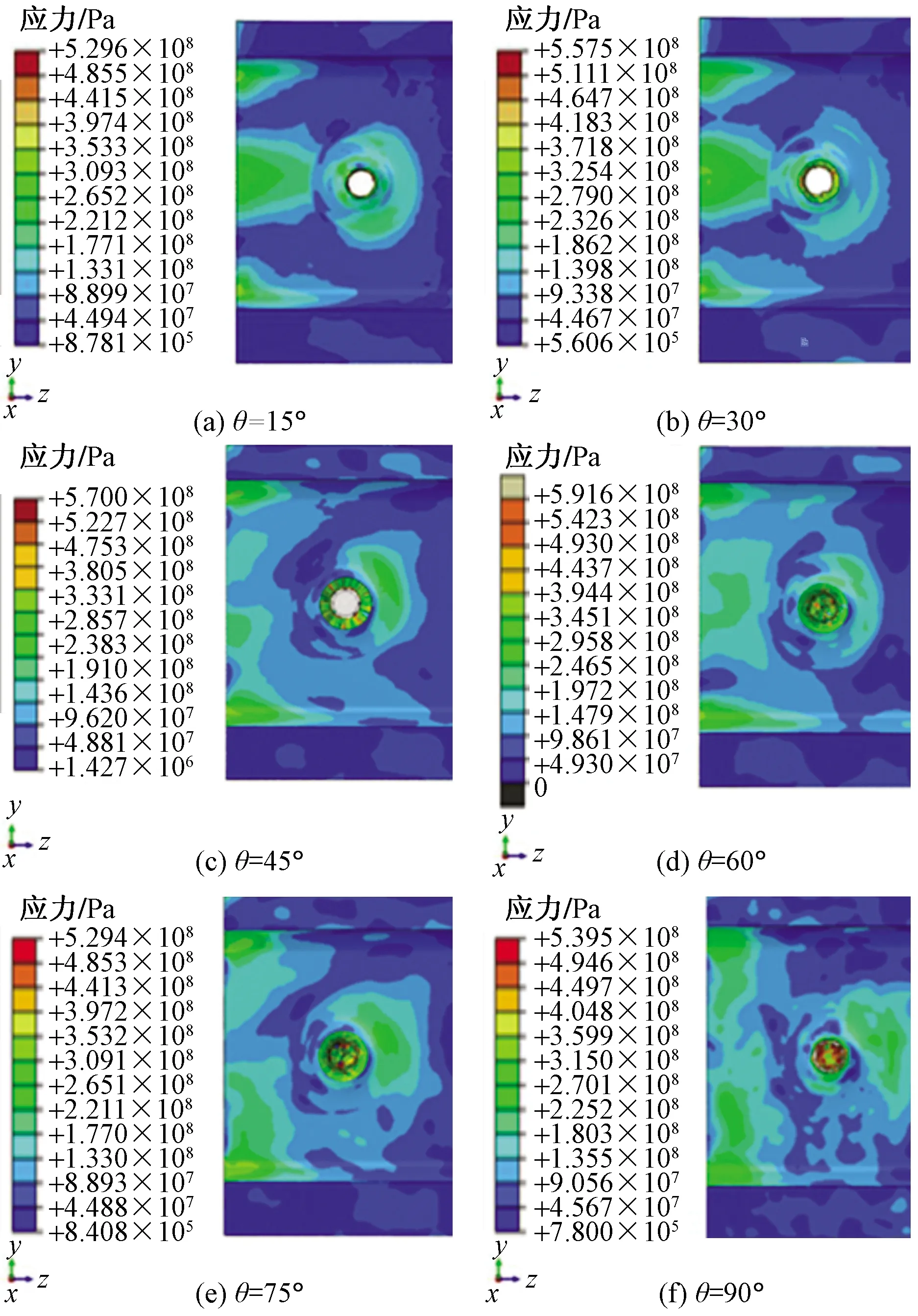
图9 铜质子弹不同弹头倾角结果图
弹头倾角为15°、30°、45°、60°、75°和90°时,对应的机身框架的最大应力分别为5.296×102、5.575×102、5.7×102、5.916×102、5.294×102和5.395×102MPa。倾角由小到大变化时,应力先增大后减小再增大,变化幅度较小;倾角为60°时,应力最大。
计算得到不同入射角下的最终子弹剩余速度分别为8.524×102、8.501×102、8.337×102、8.299×102、8.249×102和8.2×102m/s,内部最大应力和最终剩余速度随倾角变化图及子弹剩余速度随时间变化图如图10所示。
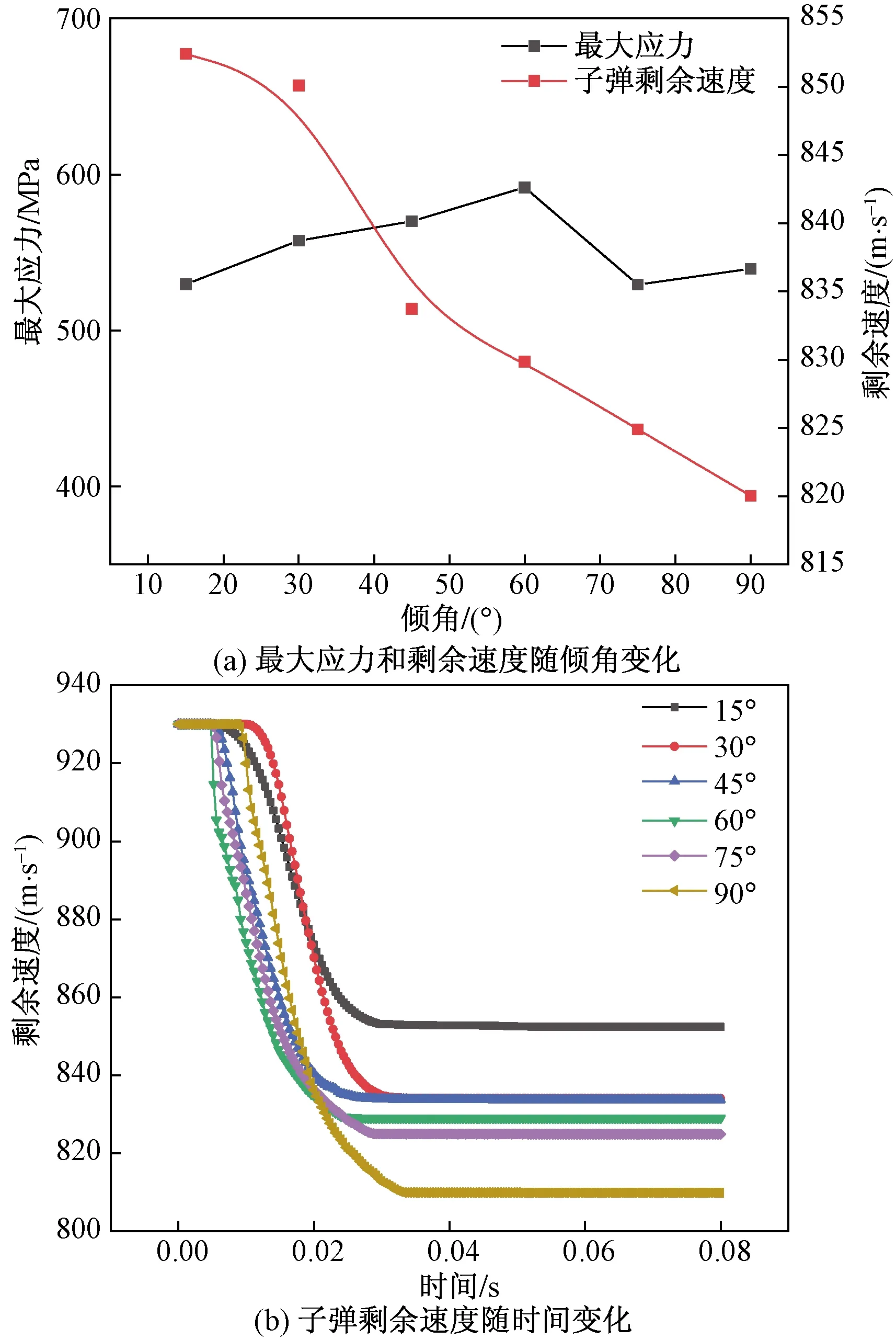
图10 铜质子弹最大应力和剩余速度随倾角和时间变化曲线图
分析得出随着子弹角度增加,框架破坏面积先增大后减小,当倾角为45°时,破坏面积最大。从内部应力角度分析,内部应力变化幅度较小,结果稳定在5.5×102MPa左右。倾角为60°时最大应力值最大,主要原因为子弹弹头顶部划分网格简化时子弹与框架结构初始接触面积最小,导致应力较大。从子弹剩余速度角度分析,随着弹头倾角的增大,子弹剩余速度变小,倾角为0°~30°时,子弹剩余速度变化幅度较小,倾角大于30°之后,子弹剩余速度变小速率增大,主要原因为弹头倾角减小使子弹撞击框架短时间内接触面积减小,增加单位面积内的冲击力,增强子弹的穿透能力,但倾角影响穿透能力存在临界值,当倾角达到临界值后再减小倾角,子弹穿透能力不再增加,故临界值为30°。
3.2 子弹材料对机身铝合金框架弹伤影响
为分析子弹材料因素的影响,选取2种材料计算结果,即铜质和钢制,参数如表1所示,同上选取6个不同弹头倾角,铜质子弹碰撞应力云图如图9所示,钢质子弹碰撞应力云图如图11所示。
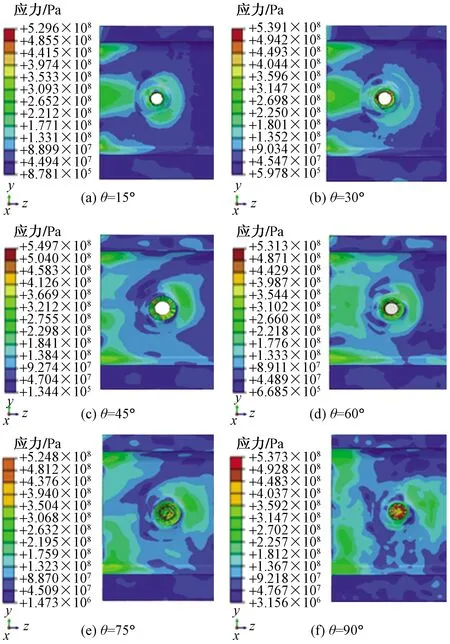
图11 钢质子弹不同弹头倾角结果图
结果表明,钢制子弹倾角为15°、30°、45°、60°、75°和90°时,对应的机身框架的最大应力分别为5.296×102、5.391×102、5.497×102、5.313×102、5.248×102和5.373×102MPa。倾角为由小到大变化时,应力先增大后减小再增大,变化幅度较小;倾角为45°时,应力最大。
计算得到钢质子弹的最终子弹剩余速度分别为8.524×102、8.481×102、8.205×102、7.932×102、7.905×102和7.84×102m/s,内部最大应力和最终剩余速度随倾角变化图及子弹剩余速度随时间变化图如图12所示。
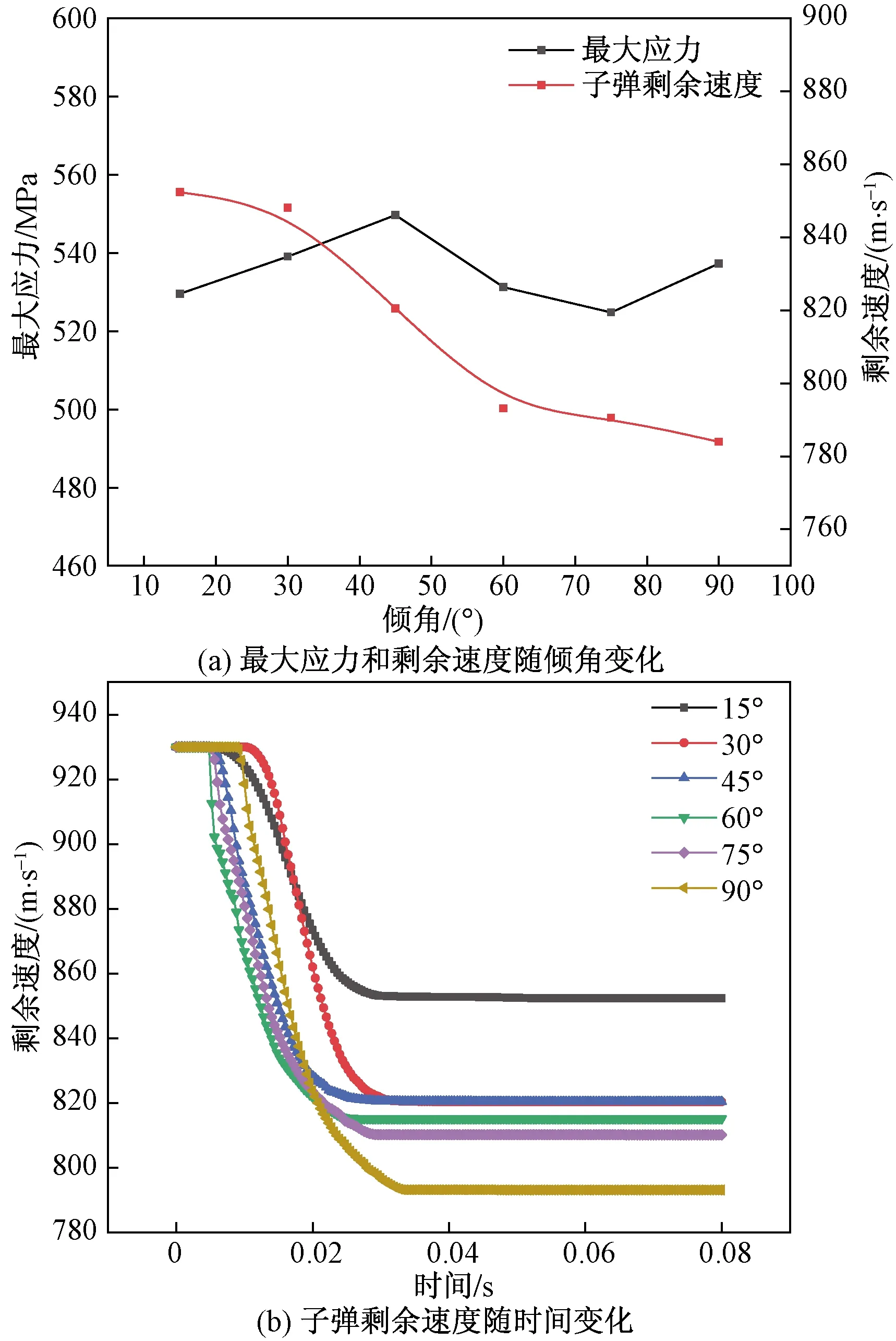
图12 钢质子弹最大应力和剩余速度随倾角和时间变化曲线图
分析得出钢质子弹随着子弹倾角增加,框架破坏面积先增大后减小,当倾角为45°时,破坏面积最大。从内部应力角度分析,内部应力变化幅度较小,结果稳定在5.4×102MPa左右,倾角为45°时最大应力值最大。主要原因同铜质子弹撞击情况。从子弹剩余速度角度分析,随着弹头倾角的增大,子弹剩余速度变小,倾角为0°~30°时,子弹剩余速度变化幅度较小,倾角大于30°之后,子弹剩余速度变小速率增大,主要原因同铜质子弹撞击情况,计算所得的临界值也为30°,两种子弹撞击时内部应力和子弹剩余速度变化规律基本吻合。
子弹的穿透力由子弹的质量和子弹运动过程中的加速度决定。由图13可知,铜质子弹加速度大于钢制子弹加速度,材料铜的密度大于材料钢的密度,故铜质子弹的穿透能力大于钢质子弹,但从子弹的破坏能力上看,由于钢材料的强度和刚度更大,故钢质子弹破坏能力更强,如图14所示。
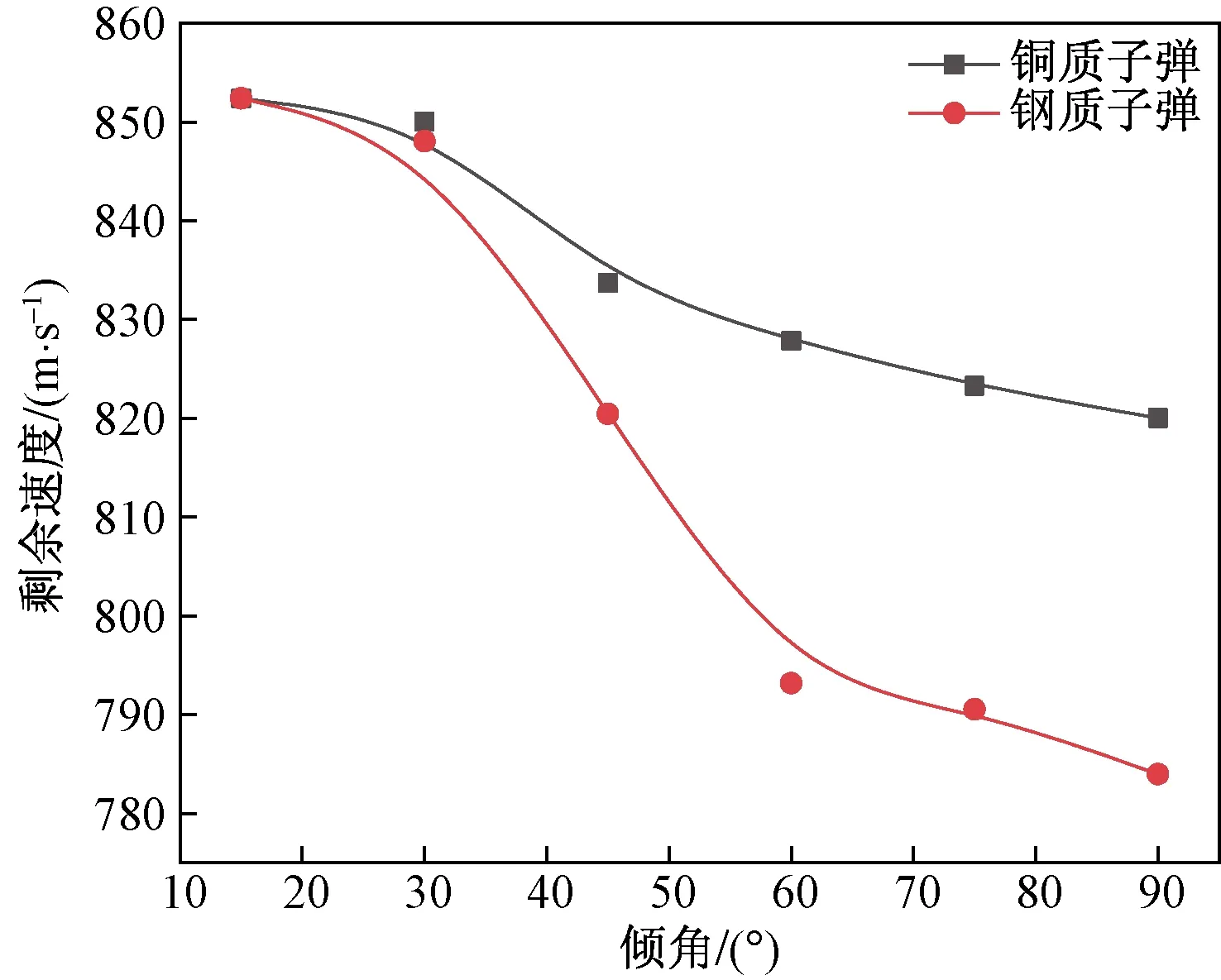
图13 铜质和钢质子弹剩余速度对比
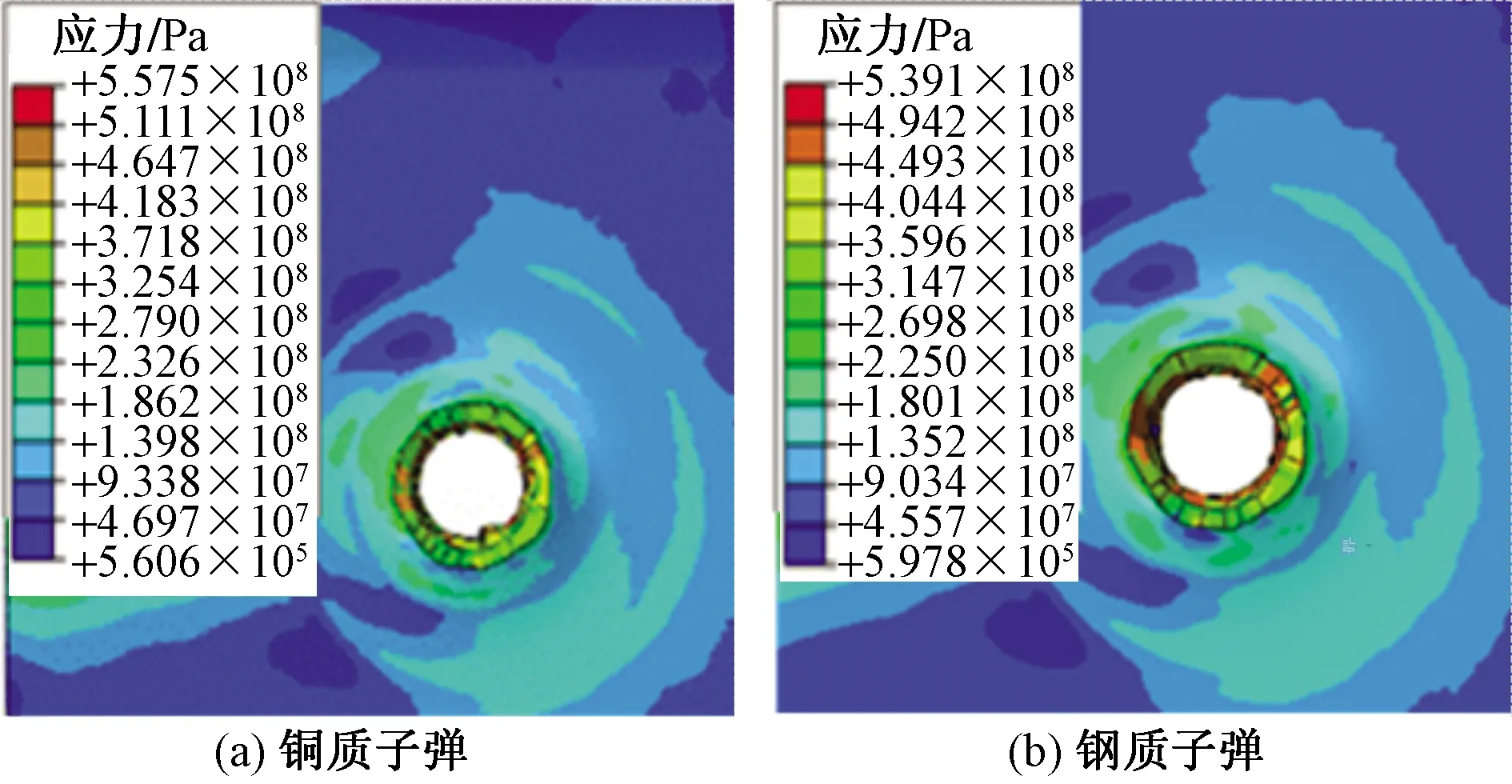
图14 倾角30°不同子弹的撞击结果比较
4 结论
(1)建立了基于修正后Johnson-Cook失效模型的弹伤冲击动力学分析模型,计算得到子弹剩余速度与实验测量结果趋势吻合较好,误差小于5%。
(2)随着时间的增加,子弹剩余速度减小速率先增大后减小,直至为0。
(3)随着弹头倾角的增大,子弹剩余速度变小,当倾角为0°~30°时,子弹剩余速度变化幅度较小,倾角大于30°之后,子弹剩余速度变小速率先增大后减小,计算结果表明弹头倾角变化影响子弹穿透能力,但影响存在临界值,当倾角达到临界值后再减小倾角,子弹穿透能力不再增加,故计算的临界值为倾角30°。
(4)子弹材料的不同影响子弹的质量和子弹运动时的加速度,影响子弹的穿透能力,计算结果表明铜质子弹的穿透能力大于钢质子弹,但钢材料的强度和刚度大于铜材料,钢质子弹的破坏能力大于铜质子弹。
