基于 HJI理论的双半球胶囊机器人姿态非线性控制方法

刘冠喜 张永顺

摘要：考虑到自主研发的双半球胶囊机器人系统不确定性以及外界扰动等非线性特征问题，提出了一种基于 Hamilton-Jacobi不等式（HJI）理论的双半球胶囊机器人滑模鲁棒非线性控制策略。通过拉格朗日动力学原理建立双半球胶囊机器人被动模态的动力学模型，并将 Hamilton-Jacobi不等式理论应用于设计滑模鲁棒的控制律来确保控制系统的稳定性。此外，通过 Lyapunov方程验证了该双半球胶囊机器人基于 HJI理论的滑模鲁棒控制系统的有效性，并对所设计的控制器进行了仿真实验，仿真和实验结果表明所设计的控制策略能有效地抑制外部干扰对控制误差的影响，提高了双半球胶囊机器人系统的控制精度。

关键词：双半球胶囊机器人;拉格朗日动力学;HJI理论;滑模鲁棒控制

中图分类号：TP242文献标志码：A

文章编号：1009-9492（2021）11-0026-04开放科学（资源服务）标识码（OSID）：

Nonlinear Posture Control Method of Dual Hemisphere Capsule Robot Based on HJI Theory

Liu Guanxi ，Zhang Yongshun

（Key Laboratory for Precision & Non-traditional Machining of Ministry of Education， Dalian University of Technology， Dalian，Liaoning 116024， China）

Abstract： Considering the nonlinear characteristics of self-developed dual hemisphere capsule robots（DHCRs） such as indeterminate and external disturbances， a sliding mode robust control strategy for the DHCR based on Hamilton-Jacobi inequality（HJI） theory was proposed. The dynamic model of the passive mode of the DHCR was established by Lagrangian dynamics principle， and the HJI inequality theory was applied to design the sliding mode robust control law to ensure the stability of the control system. In addition， the effectiveness of the control system based on the HJI theory was verified through the Lyapunov equation， and simulation experiments on the designed controller was conducted. Simulation and experimental results show that the control strategy can effectively suppress the influence of external interference on the control error， and improve the control accuracy of the DHCR.

Key words： dual hemisphere capsule robot; Lagrange dynamics; HJI theory; sliding mode robust control

0 引言

目前，可代替內窥镜检查的胶囊内窥镜机器人取得了较快的发展[1-4]，与繁琐的传统内窥镜相比，胶囊内窥镜由于具有安全，无痛等特征，可望在复杂环境中执行医学诊疗任务。按照驱动方式，胶囊内窥镜可分为被动式和主动式胶囊内窥镜。主动式胶囊内窥镜也称为胶囊机器人，主要包括电驱动式和磁驱动式胶囊机器人。由于磁驱动胶囊机器人可实现无缆驱动，并避免了复杂的行走机构，因此，磁驱动胶囊机器人具有良好的应用前景，并迅速成为国内外的研究热点。大连理工大学胶囊机器人课题组提出了一种双半球型胶囊机器人，在空间万向旋转磁场驱动随动效应驱动下，在肠胃宽裕环境下可以实现主动模态下的滚动行走和被动模态下的定点调姿[5]，通过滚动行走接近可疑目标，通过定点调姿实现对可疑目标的全景观察与筛查。空间万向旋转磁场是在三轴正交嵌套方形亥姆霍兹线圈中通入满足一定关系的三相交变电流，在三轴亥姆霍兹线圈的内部空间叠加产生的，能够消除磁力，解决磁力与磁矩相互耦合的问题，从而通过力矩的随动效应实现双半球型胶囊机器人的精确驱动[6-7]。与一般典型球形机器人采用配重块实现姿态稳定控制方式不同[8]，双半球胶囊依赖于磁场随动效应实现姿态的稳定控制，即双半球胶囊轴线与旋转磁场轴线具有跟随特性，可通过旋转磁场控制胶囊轴线在空间的位置，进而实现胶囊主动模态下滚动行进和被动模态下定点调姿两种功能。

然而，由于双半球胶囊机器人的动力学模型是一个多变量非线性系统，存在不确定性因素以及外界干扰，例如非结构化环境摩擦、肠蠕动干扰和质心位移等，这些因素对定点姿态调整的准确性具有一定影响。为了探索机器人姿态控制的动态特性，需要对非线性系统进行深入分析[9-11]。随着胶囊机器人技术的深入研究和应用场景的扩展，各种智能控制策略的应用使得胶囊机器人控制系统的非线性特性得到了较好的解决。例如，模糊控制，神经网络和专家系统以及其他非线性自适应控制方法可以通过多个简单关联来实现复杂的非线性函数，使其成为探索非线性系统的有效方法[12]。因此，本文提出了一种基于 Hamilton-Jacobi不等式（HJI）理论的滑模鲁棒控制策略，该方法解决了线性化的局限性，考虑了双半球胶囊机器人模型的不确定性以及外界扰动，使系统具有更强的稳定性和抗扰动能力。胶囊机器人非线性自适应控制的研究对于胶囊机器人的发展具有十分重大的理论意义。

1 双半球型胶囊机器人的系统原理

1.1 双半球胶囊机器人主要结构

双半球型胶囊机器人的样机及结构如图1所示，由主动半球和被动半球体两部分组成，其中主动半球体包括壳体、套筒、LED 电路、轴承、图像采集元件和径向充磁磁环等组件;被动半球体包括壳体、电池、轴及射频电路等组件。

胶囊机器人的主、被动半球体由轴承悬浮连接，在空间万向旋转磁场中，主动半球体在耦合磁矩的作用下跟随旋转磁矢量转动。当磁场法向量水平时，机器人处于主动模态下整机滚动移位模式;当磁场法向量处于竖直方位时，被动半球体在摩擦力的约束下静止，胶囊处于被动模态下定点观察模式，通过磁场方位变换可实现双半球型胶囊调姿与滚动行走双重模态分离与转换。

1.2 双半球型胶囊机器人的动力学模型

为了便于建立胶囊机器人的动力学特性的分析，建立双半球胶囊机器人的固定坐标系 Ox0y0z0和赖柴坐标系 Ox2y2z2，赖柴坐标系 Ox2y2z2表示机器人的轴线方位，赖柴坐标系 Ox2y2z2初始时与固定坐标系 Ox0y0z0重合，两个坐标系之间的相对位置及双半球胶囊机器人的运动可用俯仰角α和侧摆角β描述，先绕 Oy0轴转过α角度，得到中间动坐标系 Ox1y1z1;再将动坐标系 Ox1y1z1绕 Ox1轴旋转β角度，其坐标变换关系如图2所示。

可以得到赖柴坐标系到固定坐标系的齐次变换矩阵为：

采用拉格朗日方程建立胶囊机器人被动模态动力学模型，具有广义坐标 q 的拉格朗日机械系统的动力学方程表示为[13]：

式中：L 为机器人被动模态时系统势能和动能之和;qk为系统的广义坐标;Qk为广义力。

其动能可表示为：

L = J1（ωz 1）2+ J2（ωz 11）2+ Je （ωx 11）2+（ωy11）2

式中：ωx 1、ωy1、ωz 1分别为角速度ω′在 Ox1、Oy1、Oz1轴的分量;ωx 11、ωy11、ωz 11分别为角速度ω"在 Ox1、Oy1、Oz1轴的分量。

将式（3） 代入式（2），得到双半球胶囊被动模态动力学模型：

J （θ）θ?+ C （θ， θ? ）θ? + G （θ）+ df +Δ（ q， q? ） = T（4）

式中： T 为输入控制;df为系统外界干扰; Δ（ q， q? ） 为建模不确定部分; G（θ）为质心偏移力矩。

惯性矩阵J（θ）和离心力与哥氏力矩阵 C（θ， θ? ） 为：

式中：c11=（J1+ J2- Je ）β? sin β cosβ; c12= J1ω cosβ+（J1+ J2- Je ）α? sin β cosβ;c21=-J1ω cosβ-（J1+ J2- Je ）α? sin β cosβ;c22=0;J1、J2和 Je 分别为双半球胶囊机器人在xyz坐标系3个轴向上的主转动惯量。

2 基于 HJI理论的控制器设计

2.1 控制器设计

双半球型胶囊机器人控制系统的设计十分重要。胶囊在运行过程中，由于存在不确定性因素以及外界干扰，因此，精确建模困难。为了减少模型不确定性對系统的影响， 本文设计了一个基于 HJI理论的鲁棒控制器，将 e 设为系统的位置误差：

e（t）=θd （t）-θ（t）（7）

式中：θd （t）=[αdβd ]为双半球胶囊机器人的期望角轨迹。

设计控制律为：

T =J （θ）θ?d + C （θ， θ? ）θ?d + G （θ）μ

式中：μ为反馈控制律。

将式（8） 代入式（4） 中，可得：

J （θ）+ C （θ， θ?）e? + d = T

根据双半球胶囊机器人动力学方程，滑模构控制器滑模表面定义为：

r =e? +Λe （10）

式中：Λ= diag{Λ1，Λ2 ， … ， Λm}>0，为正定对角阵。

将式（10）代入式（9） 中，可以得到：

式中： w =JΛe? +CΛe。

根据 HJI 理论，将滑模函数作为评价信号 z ，式（11）可以改写为：

为了表示系统的抗干扰能力，定义性能指标为：

根据式（11）， Hamilton-Jacobi 不等式理论可描述为：给定任意一个正数γ，如果存在一个正定且可微的函数 L（x）≥0，同时满足：

L? ≤恳γ2|d |2-|z |2}（?d）（14）

则鲁棒条件 H ≤γ成立。

为了使得胶囊机器人控制系统满足鲁棒条件，将设计控制律为：

2.2 控制系统的稳定性分析

前文所述，通过 HJI 理论设计了一个滑模控制律，为验证其控制系统的稳定性，利用李雅普诺夫定律来分析系统的稳定性及收敛性，定义李雅普诺夫函数：

对上式求导，则：

定义：

将式（17）代入式（18）中，可以得到：

则有 I ≤0，即，满足 Hamilton-Jacobi不等式理论以及李雅普诺夫稳定性的理论条件。因此，所设计的控制系统是有效的。

3 系统仿真

本文双半球胶囊基于 HJI理论的非线性控制系统如图3所示，根据动力学模型进行运动仿真实验，以验证所提出的自适应跟踪控制方案的性能和效率。

在仿真中，系统参数配置如表1所示，给定俯仰以及侧摆运动为正弦信号，设计了以下仿真实验。

控制器中状态变量的初始值为0，滑膜控制器的控制参数Λ=diag （2020），γ=0.05，采样时间为0.001。

仿真结果如图4所示，结果显示了实际轨迹角度能够稳定跟踪预期轨迹角度，实线是 DHCR的姿态角和侧摆角的预期轨迹，虚线是胶囊机器人的姿态角和侧摆角的跟踪轨迹。

从图5所示的仿真结果可以看出，在不确定性以及干扰存在的条件下，机器人的姿态角度跟踪误差小于±2%，充分证明所提方法的有效性。

4 实验验证

实验平台包括双半球胶囊机器人和控制系统，如图6所示，控制系统由 PC和一台 DSP控制器组成，PC主要负责控制算法指令的生成，并将所需的电流通过串行端口传输到 DSP控制器，通过更改电流的幅值来改变磁矢量的方向，从而实现 DHCR的姿态调整。机器人配置了摄像头、 LED 光源、图像无线发射模块和高能量电池等集成硬件，不仅能够保证胶囊在胃肠道中稳定驱动，还能将胶囊在胃肠道中的图像以视频流的方式无线传输到PC 机上。

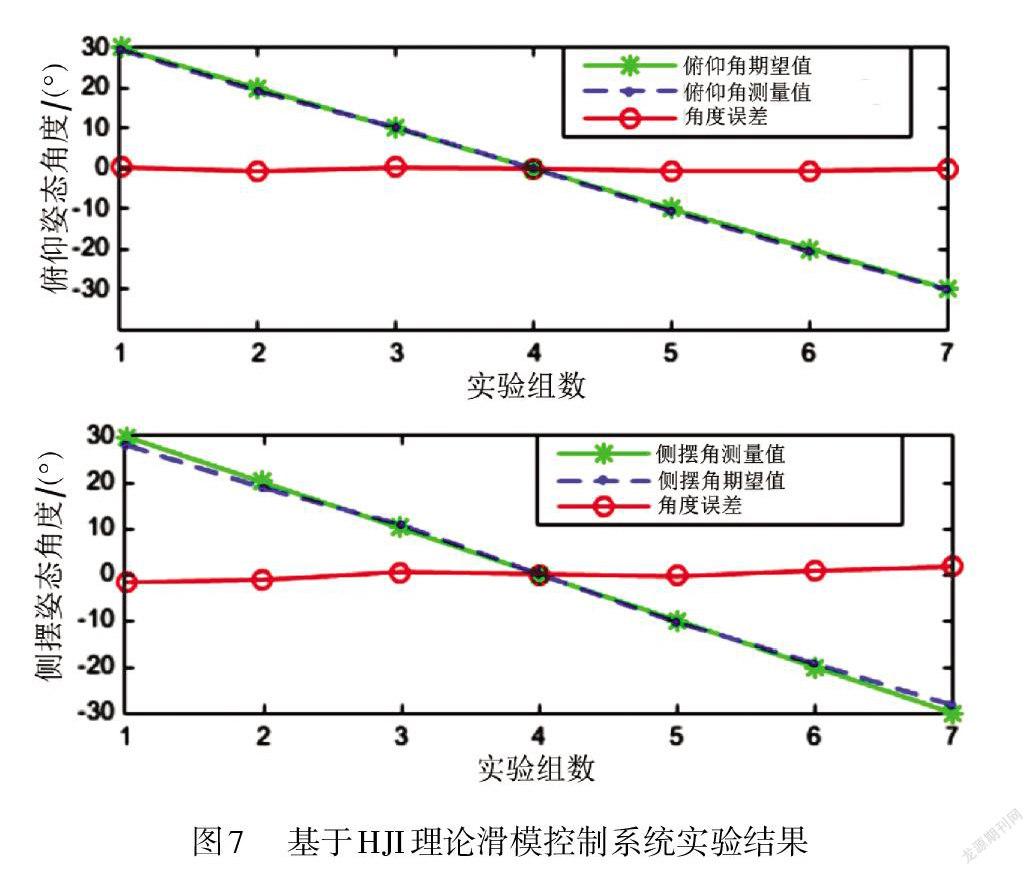
为了进一步验证 HJI 理论滑模控制系统的有效性，设计了相应实验来测试控制系统的性能。将机器人放置在人体肠道模型中，肠道模型上部铺设猪大肠，用来模拟真实肠道粘弹性环境，并将模型放在三轴亥姆霍茨线圈当中，通过 SURMF调整旋转磁矢量方向驱动机器人进行姿态调整。在实验过程中，分别对胶囊机器人的俯仰和侧摆的姿态位置进行了测试。

采用激光检测方法得到机器人的姿态信息，对不同位置的姿态数据进行记录，从图7所示的实验数据可以看出，系统的控制误差仍然存在。然而，由于胶囊机器人采用了更大的广角（140°）来实现肠胃内部的可视化，该误差范围能够满足机器人实现胃肠道的全景观察要求，因此，本文提出的控制策略可行。同时对比仿真和试验角度跟踪误差可知，试验角度跟踪依然存在一定误差，误差范围在±5%。该现象的原因，一方面是由于仿真建模时胶囊机器人模型理想化，另一方面是加工出来的胶囊机器人质量分布不均匀导致的，其他更深层次的原因则需要继续探究。