基于基追踪的位场数据稀疏反演
2021-08-19叶丽霞张玉洁
叶丽霞,张玉洁
(1.中国地质大学 数学与物理学院,湖北 武汉 430074;2.中国地质大学 地质探测与评估教育部重点实验室, 湖北 武汉 430074)
1 引 言
重磁场物性反演作为了解地下密度和磁化率分布的重要手段,在矿产、石油、工程勘探等很多领域已经有了广泛的应用。相比于参数反演,物性反演具有其特定的优势,它能够较好地提供异常体的位置、形状等信息,从而对于重磁数据的解释具有重要意义,也是该领域的一个热点。重磁勘探的主要目的是通过测量重力场源和地磁场源的数据异常,并对测量的数据进行反演和解释,从而得到地下异常源的密度分布和磁化率分布[1]。磁场物性反演指的是将地下空间的异常体看作是一系列较强或较弱的磁化强度所组成的异常区域,根据地面观测的磁异常反演地下磁化强度分布时,将地下空间介质划分为一系列块体单元,当块体单元足够小时,假设每个块体单元内部磁化强度均匀分布,允许不同块体单元具有不同的磁化强度。在反演的过程中,磁化强度是唯一需要反演的参数。这种反演方法与层析成像方法相似,因而也称磁化强度成像。
由于观测数据数目远小于模型参数数目,会导致反演问题的多解性,从而造成分辨率低的现象。基于这种现象,人们提出了许多反演理论,其中包括联合反演和约束反演[2]。Pilkington[3]将预优共轭梯度算法用来求解磁数据离散反演问题,减少了计算量,提高了反演效率。Li等[4]在目标函数中加入了深度加权函数,以此来克服反演结果的“趋肤效应”。这套反演理论虽然稳定性好,但是得到的反演结果比较发散。此外,他们还将地表全磁数据与钻孔三分量磁数据进行反演,这种联合反演方法有效地提高了反演的分辨率[5]。Sun等[6]在反演算法中加入了已知的物性信息,进一步改进了反演模型。此外,反演的方法还包括基于L2范数的正则化光滑反演方法[7]、基于L0范数的正则化聚焦反演方法[8]、二元和多元聚焦反演方法[9]等。总而言之,这些方法都是为了解决重磁场反演的多解性问题以及分辨率低的问题。
传统重磁反演可以采用观测数据和模型参数的L2范数极小化,L2范数易于处理,容易求解。但L2范数获得的是非稀疏解,在稀疏重构方面所得的解稀疏性差,会增大非零值的范围,降低了反演的分辨率。压缩感知[10]理论能很好地刻画稀疏性,该理论指出,只要信号是稀疏的或者能够被稀疏表示,那么就可以无失真地重构出原始信号。在压缩感知的推动下,Lp范数(0≤p≤1)优化在理论和算法上有了巨大的发展[11,12],这为求解Lp范数稀疏反演问题提供了理论基础。Li等[13]将物性上下界不等式约束添加到目标函数中,用内点法处理优化问题,对三维位场数据进行Lp范数稀疏反演。此外,零范数稀疏恢复在地球物理领域也得到了广泛应用[14,15]。Meng等[16]提出了一种基于稀疏恢复的三维重力反演方法,选取L0范数作为目标函数,然后用近似零范数函数迭代求解。在过去的十几年里,压缩感知理论得到了较为成熟地发展,在很多领域有了广泛应用。压缩感知用于地震数据反演已经取得了较好的效果[17,18],越来越多的研究者尝试将压缩感知用于重磁数据反演。
本文提出基于基追踪的重磁场物性稀疏反演方法,用压缩感知技术代替传统的反演方法,直接从反演模型出发,并且引入物性上下界约束,构建目标函数,将其转化为有约束的优化问题,然后利用基追踪对数障碍规划算法进行求解。
2 基本原理
2.1 正演
重磁异常的正演计算表达式可表示为:
Gm+e=d
(1)
其中,G是核矩阵,维度为M×N(M 重磁场物性反演的过程就是利用观测数据向量和核矩阵来估计模型参数向量。传统的反演方法得到的是分辨率比较低的非稀疏解,而大多数情况下,物性分布本身就是稀疏的,因而本文采用压缩感知理论对重磁场物性进行反演。压缩感知模型如下: y=Ax (2) 其中,y是M维的观测向量;A表示测量矩阵,维度为M×N(M 由于M (3) Li等[19]指出零范数的求解是NP难问题,但是当满足一定条件的时候,L1范数最小化和L0范数最小化是等价的,因而式(3)可以转化为下式: (4) 式(3)的求解比较常用的是凸优化算法和贪婪算法。贪婪算法虽然速度快且精度相当,但是贪婪算法大多数需要知道信号的稀疏度。而凸优化算法是将式(3)转化为凸优化问题,并求解目标函数得到全局最优解。比较典型的L1范数最小化求解方式是基追踪(Basis Pursuit, BP)算法,BP算法的精度高,本文选用的是基于对数障碍规划算法的基追踪反演方法。 考虑到L1范数对稀疏度的刻画比较容易求解,本文将常规的基追踪方法对噪声的压制的L2范数改为L1范数的约束,那么基于压缩感知理论的基追踪反演问题表示为: (5) 其中,m=(m1,m2,…,mN)表示异常体的磁异常;ε表示噪声强度。 式(5)所示的目标函数没有考虑深度加权,容易使反演结果趋于地表。因此,考虑加入深度加权Wm,其形式与文献[4]中基本一致,只是参数设置不同。同时我们也引入数据加权矩阵Wd,无噪声情况下,其形式为: (6) 其中,σ为观测数据的标准差;I为单位矩阵。 为方便采用上述算法进行求解,令 (7) 则式(5)可变为: (8) 由拉格朗日乘子法,式(8)可转化为求解下式优化问题: (9) 其中,λ为拉格朗日参数。 式(9)的求解可以根据文献[20],基于改进的基追踪反演方法的目标函数,令m=x-y,dnew-Gnewm=z-w,其中xi=(mi)+,yi=(-mi)+,zi=(dnew-Gnewm)+,wi=(-dnew+Gnewm)+;可以推导出下式: z-w+Gnew(x-y)=dnew (10) 式(10)可以写成下式: (I,-I,Gnew,-Gnew)(z,w,a,b)=dnew (11) 其中,I为单位矩阵,进一步令(I,-I,Gnew,-Gnew)=D,(z,w,a,b)=c,dnew=b,k=(1,…,1,λ,…,λ)T,则式(9)的求解与下式的优化问题等价: (12) 式(12)的求解可以采用对数障碍规划算法。 由于反演的物性参数会出现负值和超出范围的现象,对求解后的结果进行如下约束: 0≤m≤mmax (13) 其中,mmax指的是物性参数的下界,一般是已知的。 本节将在模拟数据和实际数据上验证该算法的性能,并与传统的基于L2范数的共轭梯度法[21]进行对比。 模拟数据实验选取的是6种二维磁性棱柱体模型分别是直立板状体模型、平行竖直板状体模型、倾斜板状体模型、向斜模型、断层切割模型和垂向尖灭模型。模拟实验假设异常体都是被均匀磁化的,磁化强度大小为M=100 A/m,磁化倾角为I=45°,测线磁方位角为A=0°,即有效磁化倾角为45°。观测数据的点间距为20 m,观测点个数为51个。地下异常体研究空间被剖分为800个网格单元,即20行40列,网格单元是边长为25 m的正方形。用共轭梯度算法和基于对数障碍规划算法进行二维磁化强度反演,选取的上下界范围在0~100 A/m内,反演结果见图1~图6,图中色标柱为磁化强度M,单位为A/m。 图6 垂向尖灭模型反演结果Fig.6 Vertical pinch model inversion result image 以图1进行说明, 图1(a)和图1(c)分别表示对数障碍规划算法和共轭梯度算法观测数据和预测数据的拟合曲线,可以看出两个算法拟合都非常好;图1(b)和图1(d)分别表示直立板状体模型对数障碍规划算法和共轭梯度算法的反演结果,白色边框表示理论模型的轮廓,从中可以看出共轭梯度法的成像结果大致体现了地下异常体的位置,但是边界的反演却很模糊,得到的磁化强度大小为50~70 A/m。而用压缩感知技术的对数障碍规划算法得到的磁化强度大小更接近真实值100 A/m。其他模型的反演结果类似,因而对数障碍规划算法能够获得物性的稀疏分布,相比传统的物性反演方法,稀疏重构的结果分辨率得到提高,可以获得具有尖锐边界的反演结果,对目标地质体的定位更加准确。 图1 直立板状体模型反演结果Fig.1 Upright plate model inversion result image 图2 平行竖直板状体模型反演结果Fig.2 Parallel vertical plate model inversion result image 图3 倾斜板状体模型反演结果Fig.3 Inclined plate model inversion result image 图4 向斜模型反演结果Fig.4 Syncline model inversion result image 图5 断层切割模型反演结果Fig.5 Fault cutting model inversion result image 实际数据选择的是青海省尕林格铁矿保护区,将本文方法应用于该地区[22],对铁矿区两条沿测线的剖面数据进行反演解释。图7显示的是青海省尕林格矿区磁异常平面等值线图,该区各磁异常分布明显,磁异常的幅值最高为1 600 nT。该矿区的主磁铁矿被大面积的砂砾层围岩所覆盖,反演结果图中Mt为围岩中出露的磁铁矿体[23]。该矿区磁铁矿的平均磁化强度是40 A/m,因此设置磁化强度上下界范围0~40 A/m。对于该地区的磁力数据反演,前人已经做过很多工作[24,25]。因此,本方法只是用来验证该算法在实际数据反演中的有效性。212和196两条平行测线穿过主要的磁异常矿体暴露区域而且两条平行测线均经过很多钻孔点,对于后续反演测线结果的验证具有重要意义。每条平行测线的总长为1 200 m,点间距设置为20 m,即观测点数据为61个,将地下空间均匀剖分为20行48列,网格单元是边长为25 m的正方体,反演结果见图8和9。 图7 青海省尕林格矿区磁异常平面等值线[22]Fig.7 Plane contour map of magnetic anomaly in Galinge mining area, Qinghai province 以图8进行说明,图8(a)表示数据拟合曲线图,图8(b)表示212测线反演结果图。从图8中可以看出,212测线反演出来的异常体区域的位置大致与钻孔剖面反映出来的信息相符合,但是在一定程度上未能够反映矿体的倾斜方向,而且更深层的位置没有反演出来。图9中196测线右边反演出来的异常体区域大体上也符合钻孔信息,但是也存在212测线深层区域没有反演出来的问题。另外,196测线左边的反演结果是未经过钻孔验证的,只能推测测线左边的矿体位于300~400 m左右的位置,且矿体规模小于测线右边。 图8 尕林格铁矿区212测线成像效果示意图Fig.8 Schematic diagram of imaging effect of 212 survey line in Galinge iron ore area 图9 尕林格铁矿区196测线成像效果示意图Fig.9 Schematic diagram of imaging effect of 196 survey line in Galinge iron ore area 本文突破传统的反演理论,将基于对数障碍规划的算法用于位场数据反演。模拟数据和实际数据实验结果表明,与传统反演方法相比,该方法不仅可以快速反演位场的稀疏分布,而且可以获得分辨率高、具有尖锐边界的反演结果。下一步的工作将进一步从实际问题出发,增加联合反演的工作,从而更好地解释反演结果,并改进算法对深层区域加以改善。2.2 反演
3 实 验
3.1 模拟数据实验
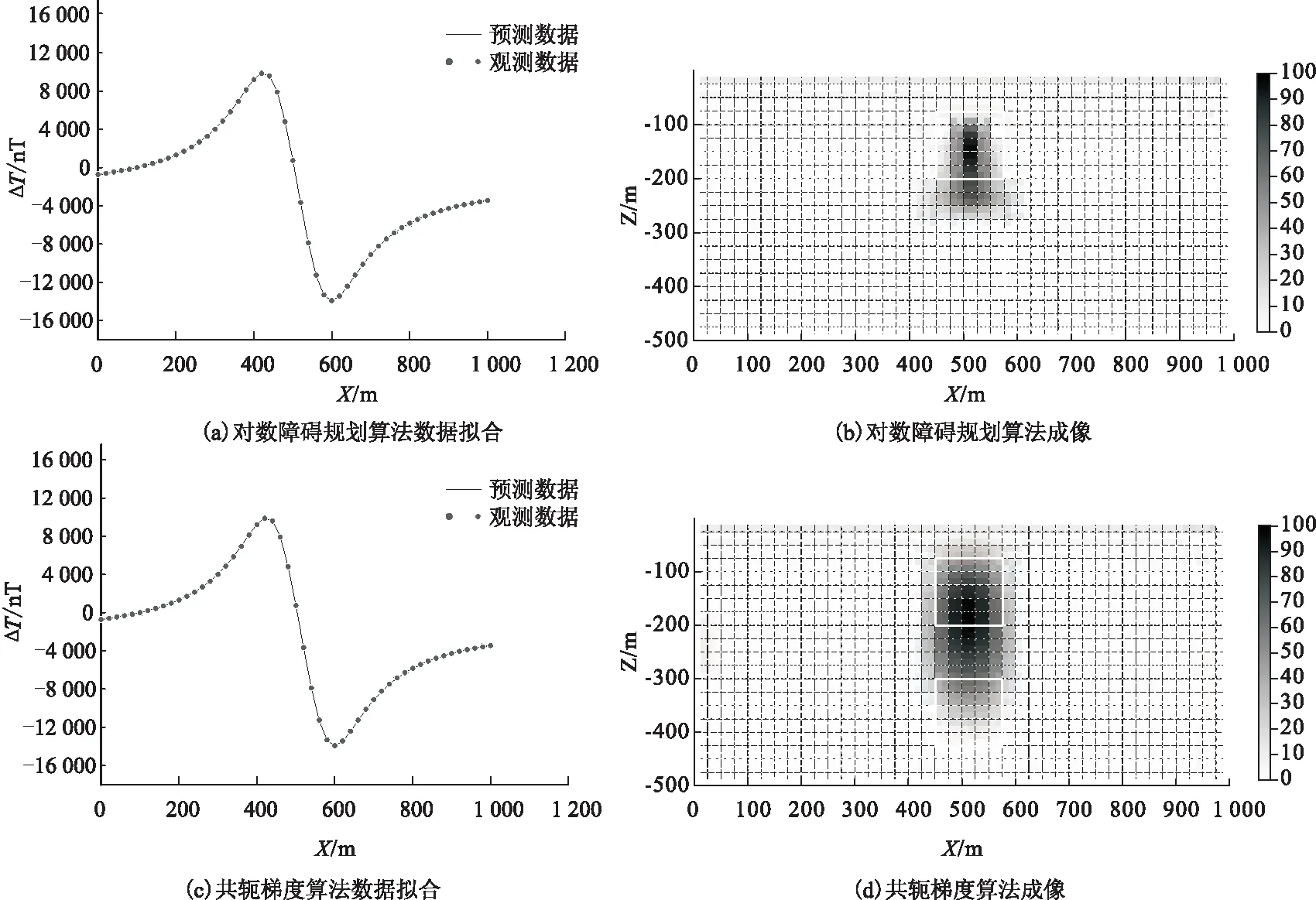
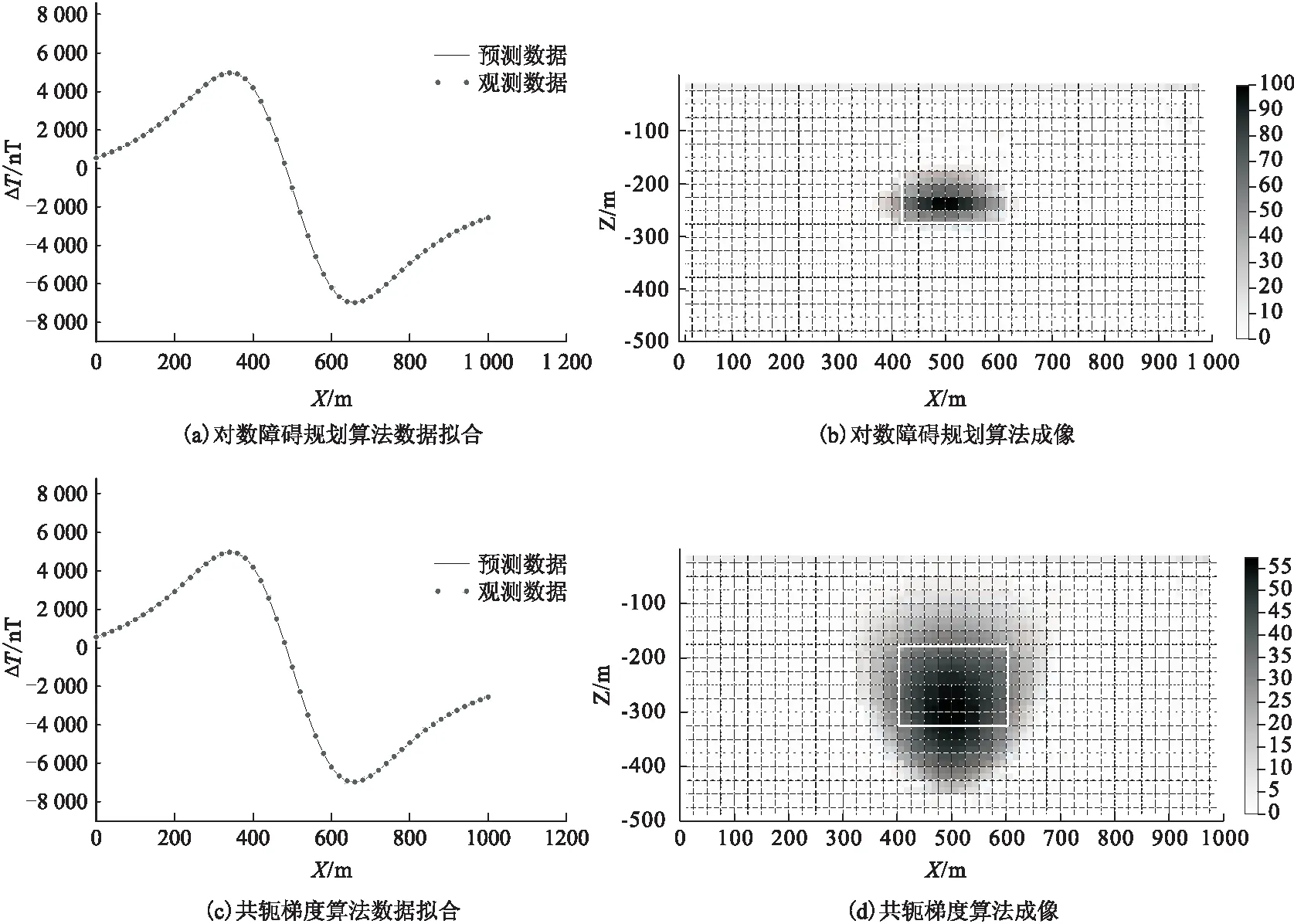

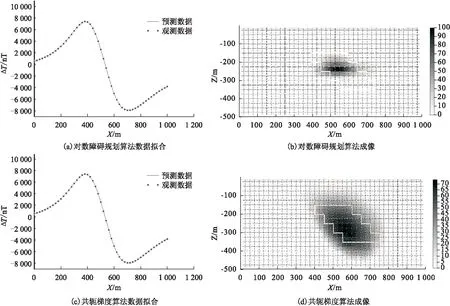


3.2 实际数据实验
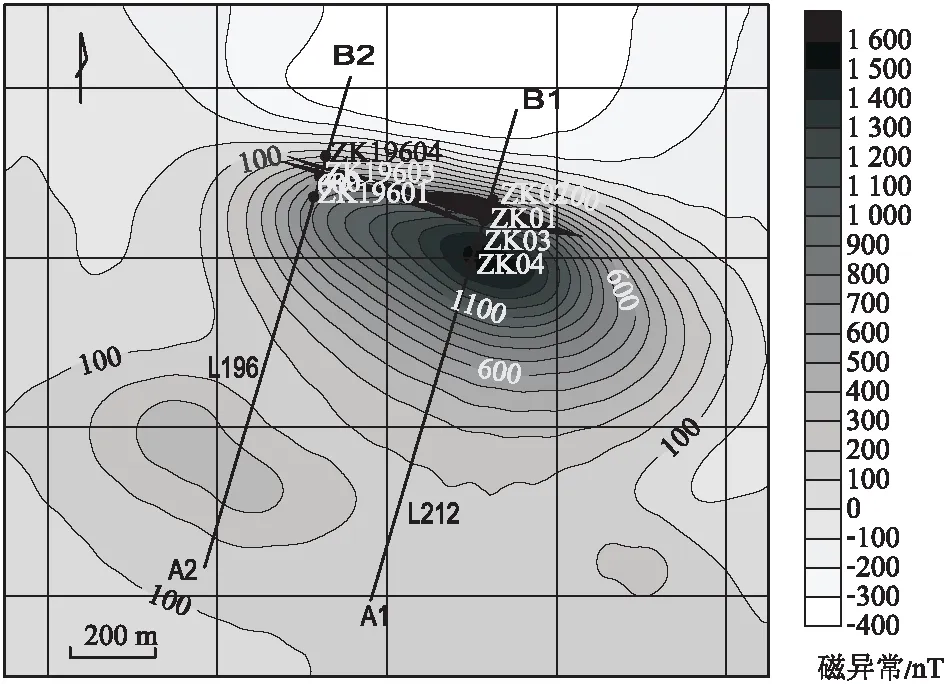


4 结 论
