强剩磁强退磁条件下的二维井中磁测反演

刘 双，冯 杰，高文利，邱礼泉，刘天佑，胡祥云＊

1中国地质大学 地球物理与空间信息学院，武汉 430074

2中国地质科学院 地球物理地球化学勘查研究所，河北廊坊 065000

1 引 言

强剩磁和强磁性体的退磁作用改变了磁化强度的大小和方向，导致磁异常的幅值和形态畸变，影响磁测资料的反演解释.研究表明，当磁化率κ≥1.0 SI时，考虑退磁与不考虑退磁作用异常极大值相对偏差可达30%以上［1］.近年来，国内外学者对剩磁和退磁的影响做了大量的研究［2－4］，但是对其反演的研究还不足.目前，研究剩磁、退磁条件下磁场反演的方法主要有两种：一是反演总磁化强度的大小和方向.如王妙月（2000，2004）等通过反演磁化强度的三个分量最终获得磁化强度大小和方向的分布［5－6］.Dannemiller和Li（2006）用地面化极异常垂直梯度和总梯度的相关系数来估计总磁化强度的倾角和偏角［7］.Shearer和 Li（2004）利用磁异常转换模量（MMTs）估算磁化强度的方向［8］.Krahenbuhl和Li（2007）认为退磁与剩磁具有类似之处，就是影响单个磁性体单元的磁化强度方向和大小，所以先估计磁化强度方向，然后用化极异常的总梯度模数据反演磁化强度大小［9］.二是通过求解边值问题，直接恢复物性分布.如Lelièvre和 Oldenburg（2006，2009）用有限差分法重建地下高磁化率磁性体的三维磁化率分布取得较好效果［10－12］.

近年来，我国加紧对老矿山深部及外围的矿产资源勘查，使井中三分量磁测仪器和观测技术取得重要进展，但是井中三分量磁测数据的反演解释技术还比较单一，仍然是定性、半定量解释为主.例如，根据磁异常矢量的发散或收敛情况定性判断矿头矿尾的方位和深度［13－15］，通过井中磁测联合地面磁测的方式提高横纵方向上的分辨率［16－18］.井中三分量磁测具有靠近深部场源，远离浅部干扰，含有丰富的异常信息等优点.

井中三分量磁测的模量定义为Ta＝（X2＋Y2＋Z2）1/2，它的主要优点在于它弱敏感于磁化强度方向.且二维磁异常模量完全不依赖于磁化方向［19－20］.地面磁异常模量Ta通常由总磁场强度异常ΔT在频率域中通过分量转化得到［21－24］，但是当有很强的剩磁和退磁作用时，在频率域中计算的磁异常三个分量将会产生较大的误差，无法获得更准确的模量数据.然而，井中磁测直接提供观测的磁场分量，由它可以得到准确的磁异常模量.

本文以二维情况为例，模拟剩磁及退磁作用下的磁场特征，并充分利用井中磁测的振幅和相位信息，研究感磁、剩磁和自退磁作用下的井中磁测反演.

2 二维井中磁测磁化强度矢量反演

2.1 二维井中磁异常模量

二维情况下的井中磁异常模量Ta定义为

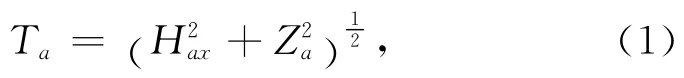
其中，Hax和Za分别为磁场的水平分量和垂直分量，Hax和Za由各个单元体产生异常的叠加，即

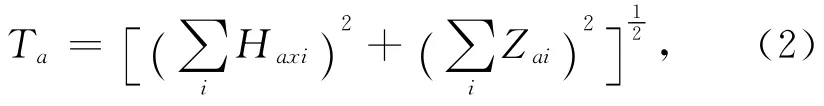
对于单个磁性单元的磁异常模量为

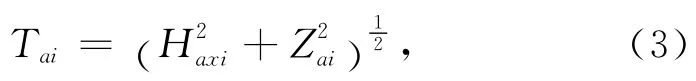
由式（2）、式（3）可知，

式（4）说明，井中磁测的磁异常模量不满足叠加性.因此，在计算剖分磁性体的磁场模量时，不能将单个磁性体单元的磁场模量直接叠加.

由于二维磁异常模量Ta完全不依赖于磁化方向，且异常极大值对应着磁性体的中心［19］.因此，我们首先可以根据井中磁测的磁异常模量，反演磁化强度大小的分布.

2.2 磁化强度大小反演

井中磁测磁异常模量Ta与磁化强度大小m是非线性的，它们的关系可写为

Ta（m）为非线性函数，对（5）式进行一阶泰勒展开得线性方程组

ΔTa为磁异常模量观测数据Ta的前后两次迭代的修正量，Δm为模型参数矢量m的前后两次迭代的修正量.JTa为雅可比矩阵，表示磁异常模量观测数据对模型参数的变化率，其元素JTa（i，j）为

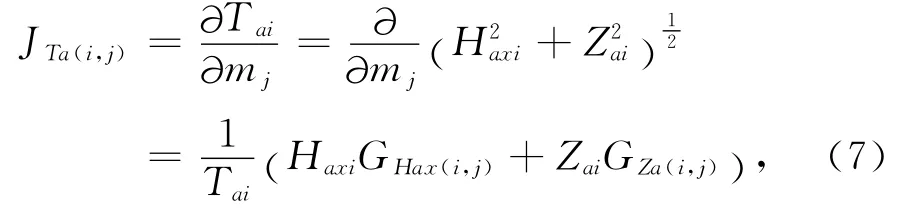
i（i＝1，2，…，m）表示第i个观测点，j（j＝1，2，…，n）表示第j个网格单元，m和n分别表示观测点总数和网格单元总数，Haxi、Zai和Tai分别表示第i个Hax、Za和Ta异常.GHax、GZa分别为Hax、Za分量对模型参数的雅可比矩阵，其第（i，j）元素分别为

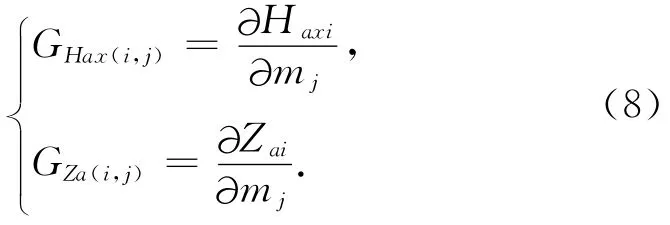
（6）式矩阵方程的最小方差解等价于求解正定方程

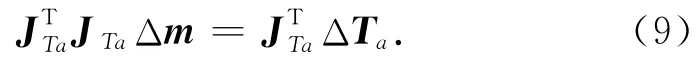
在方程（9）等式两边同时乘以一预优矩阵改善方差的条件数，即

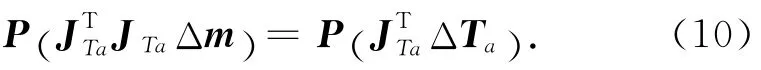
给定初始模型m0后，用预优共轭梯度法求解方程（10）得到模型修正量Δm，通过多次迭代，求得最优解m＊.

2.3 磁化强度方向反演

磁异常水平分量Hax和垂直分量Za与磁化强度方向I的关系也是非线性的，设

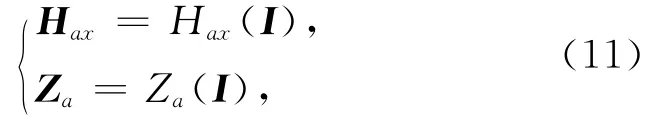
式中，Hax（I）和Za（I）为非线性函数.对式（11）一阶泰勒展开，写为矩阵方程形式

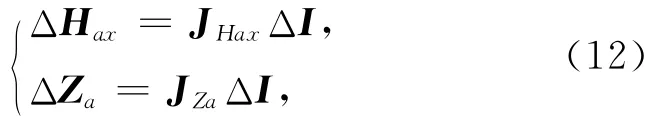
式中，ΔHax和ΔZa分别为Hax、Za异常前后两次迭代的修正量，ΔI为磁化强度倾角I前后两次迭代的修正量.JHax和JZa为雅可比矩阵，其元素JHax（i，j）和JZa（i，j）分别表示在第i个观测点的Haxi和Zai异常对第j个模型参数Ij的变化率，即

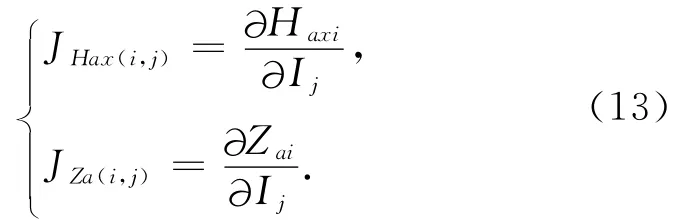
解方程（12）等价于求解正定方程

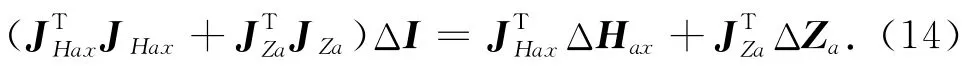
同求解方程（9）类似，用共轭梯度法求解方程（14），但不必进行预优处理.

3 预优共轭梯度法

共轭梯度法是求解（9）、（14）大型正定方程的最有效方法之一，在地球物理反演中得到广泛的应用，如地震层析成像、大地电磁反演、电阻率成像、密度成像等［25－27］.

3.1 预优矩阵

对于磁化强度反演来说，方程（9）系数矩阵的条件数是相当大的，严重影响共轭梯度算法的收敛.为提高收敛速度，Pilkington（1997）采用预优矩阵改善方程条件数，并提出求解类似方程的预优共轭梯度算法［25］.他将矩阵方程（9）修改为如下形式：

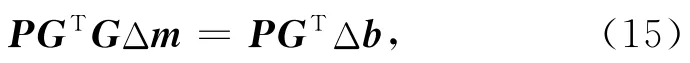
式中，G 为核矩阵，P为预优矩阵，近似等于（GTG）－1，即P（GTG）≈I（I为单位阵）.

本文磁化强度反演，取预优矩阵P为对角阵：

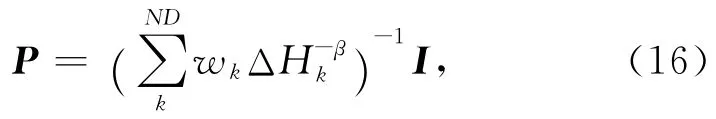
其中，ND为钻孔的数量，wk为第k个钻孔的权重系数，ΔHk为第k个钻孔的井轴到单元体的距离，β为与磁异常衰减速度有关的常数.理论上，对于二维反演，β＝4.0；对于三维反演，β＝6.0.式（16）预优矩阵P，抵消了核矩阵GTG对角元素的急剧衰减，使得PGTG的奇异值集中分布在对角线上，改善了方程的条件数，提高了共轭梯度法的收敛速度和反演的分辨率.

图1是β不同取值（0.0～7.0）时的井中磁测模量异常的磁化强度大小反演结果.反演结果说明，当β＝0.0时，没有预优矩阵的作用，此时磁化强度集中分布在ZK1、ZK2的井轴周围，出现“趋肤效应”现象.随着β的增大，分辨率逐渐提高，“趋肤效应”逐渐减弱.当β≥3.0时，“趋肤效应”消失，反演效果有很大改善.当3.0≤β≤4.0时，反演的效果最好.

3.2 磁化强度大小反演的步骤

磁化强度大小反演，求解方程（9）需要引入预优矩阵.对于磁化强度方向的反演，求解方程（14）时不需要引入预优矩阵.磁化强度大小反演的步骤为：

（1）给定初始模型m0＝0；

（2）令i＝0，计算JTa，i，dTa，i＝Ta（mi），ΔdTa，i＝dTa－dTa，i；

（3）若 ‖ΔdTa，i‖ ≤ε（ε为收敛误差），输出最优解mi，反演结束；否则执行第（4）步；

（5）zj＝Prj，若j＝0，则pj＝zj，否则βj－1＝

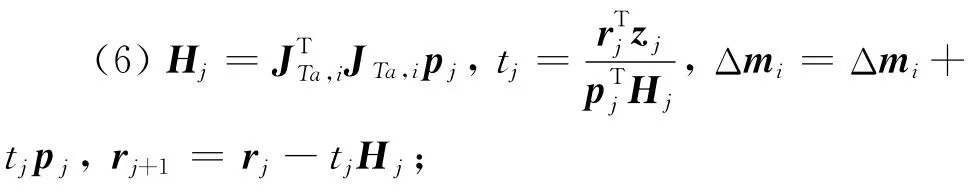
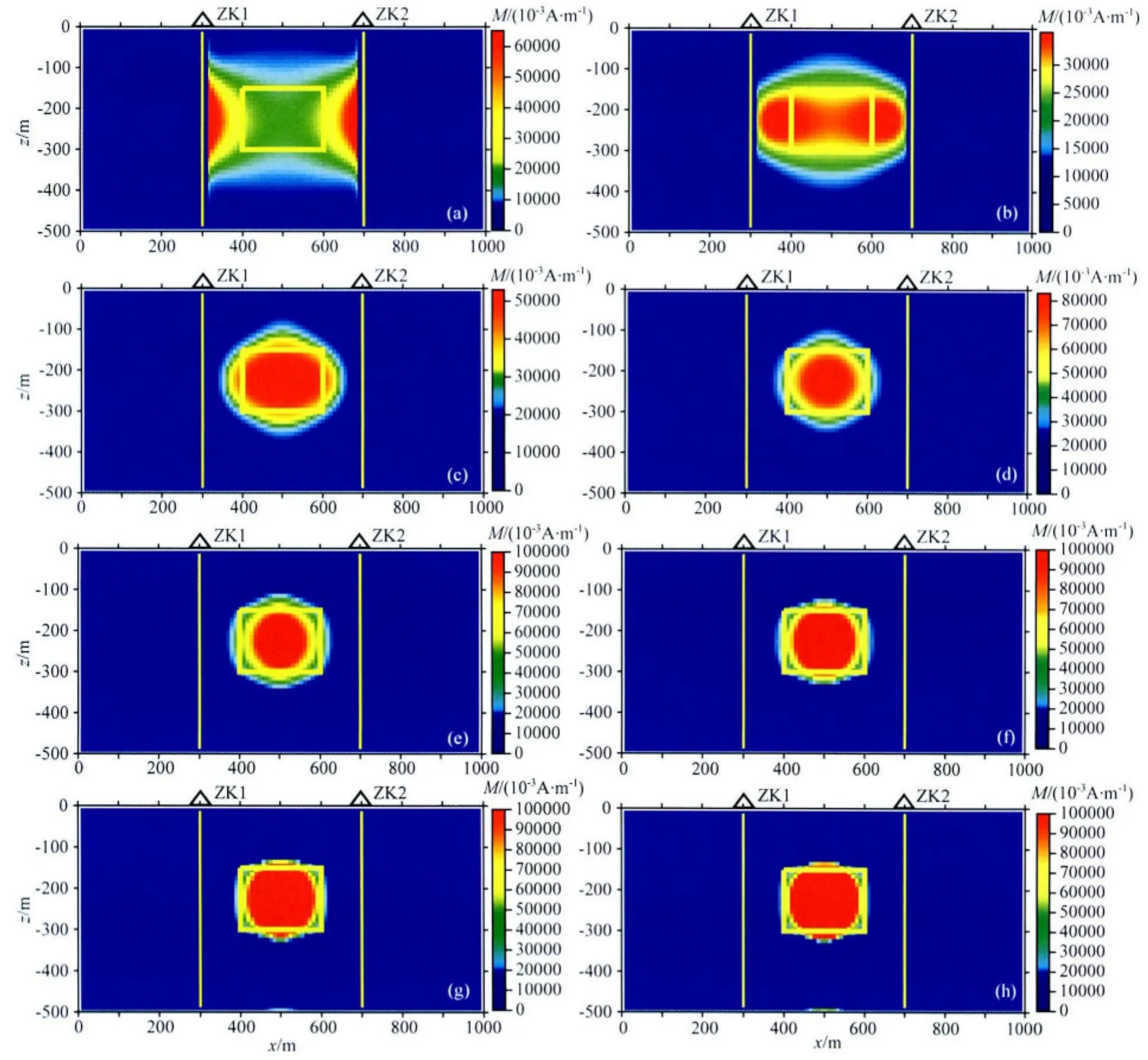
图1 不同β值的井中磁异常模量的磁化强度大小反演结果Fig.1 Magnetization intensity inversion results of borehole magnetic anomaly amplitudes for different β values

（7）若 ‖pj‖ ≤εPCG（εPCG为预优共轭梯度法收敛误差），执行第（8）步，否则j＝j＋1，执行第（5）步；

（8）mi＋1＝mi＋Δmi；

（9）若 mi＋1＜ mmin，则 mi＋1＝ mmin，若 mi＋1＞mmax，则mi＋1＝mmax；

（10）i＝i＋1，执行第（3）步.

3.3 磁化强度方向反演的步骤

（1）给定初始模型I0＝0；

（2）令i＝0，计算JHax，i和JZa，i，dHax，i＝Hax（Ii），dZa，i＝Za（Ii），ΔdHax，i＝dHax－dHax，i，ΔdZa，i＝dZa－dZa，i；

（3）若 ‖ΔdHax，i‖＋‖ΔdZa，i‖ ≤ε（ε为收敛误差），输出最优解Ii，反演结束，否则执行第（4）步；

（5）zj＝rj，若j＝0，则pj＝zj，否则βj－1＝

（7）若 ‖pj‖ ≤εCG（εCG为共轭梯度法收敛误差），执行第（8）步，否则j＝j＋1，执行第（5）步；

（8）Ii＋1＝Ii＋ΔIi；

（9）若Ii＋1＜Imin，则Ii＋1＝Imin，若Ii＋1＞Imax，则Ii＋1＝Imax；

（10）i＝i＋1，执行第（3）步.

4 理论模拟：磁化强度矢量反演

设计两组模型，分别为二维矩形截面棱柱体单个模型（图2）和二维不同板状体截面棱柱体组合模型（图3），检验磁化强度矢量反演的效果.

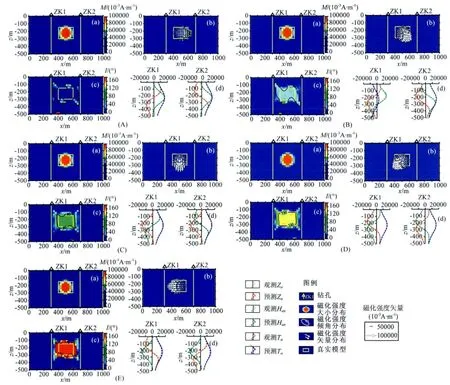
图2 二维单个矩形截面棱柱体模型不同磁化方向的井中磁测磁化强度矢量的反演结果Fig.2 Magnetization vector inversion results of different magnetization inclinations for borehole magnetic data of the 2D rectangular prism model

4.1 单个模型

假设二维矩形截面棱柱体的宽度为d＝200m，下延深度l＝150m，中心坐标（x0，z0）＝（500m，225m）.有效磁化强度大小M＝100000×10－3A/m，有效磁化倾角分别为I＝0°、45°、90°、135°、180°.在磁性体的左右两侧x＝300m和x＝700m处，分别有两个垂直钻孔ZK1和ZK2（如图2），井深均为500m.ZK1、ZK2的水平分量异常、垂直分量异常和模量异常曲线如图2（d）所示.由图可知，不同磁化方向时，水平分量异常（图2（d）红色曲线）和垂直分量异常（图2（d）绿色曲线）是不一样的，因磁化方向的变化而变化，而它们的模量异常（图2（d）蓝色曲线）是相同的，说明磁化方向变化不会引起磁异常模量的变化，即井中磁异常的模量与磁化方向无关.

图2A、2B、2C、2D、2E分别为I＝0°、45°、90°、135°、180°时，ZK1、ZK2井中磁测的磁化强度矢量反演的结果.反演时，首先根据井中水平分量异常和垂直分量异常计算出模量异常，由于模量异常与磁化方向无关，只与磁化强度大小有关，所以先用模量异常反演出磁化强度大小的分布，在已知磁化强度分布的情况下，去拟合水平分量和垂直分量，得到磁化倾角的分布.求解磁化强度大小和方向均用共轭梯度法，不同的是，在求解磁化强度大小时，需引入预优矩阵，否则反演的分辨率低，磁化强度分布将集中在井轴的周围，出现严重的“趋肤效应”现象.图2A—2E的各图中，小图（a）是磁化强度大小的反演结果，小图（c）是磁化强度倾角的反演结果，小图（b）是综合磁化强度大小和方向的磁化强度矢量结果，小图（d）是观测和拟合的ZK1、ZK2井中水平分量异常、垂直分量异常及模量异常.

反演结果说明：（1）不同磁化倾角情况下，反演的结果都很好地拟合了ZK1、ZK2井中水平分量、垂直分量和模量异常，反演过程稳定收敛.（2）5种不同情况下的井中磁异常模量是相同的，因此，5种情况下的磁化强度大小的反演结果也相同.共轭梯度法反演引入预优矩阵，反演的分辨率高，磁性边界清楚，且磁化强度的分布与理论模型吻合很好，磁化强度大小的反演效果好.（3）计算出磁化强度大小的分布后，再去拟合ZK1和ZK2水平分量和垂直分量数据，得到磁化强度倾角.反演得到磁化强度倾角的分布与外加的地磁场方向很好吻合，磁化强度倾角的反演效果好.（4）综合磁化强度大小和方向的反演结果，总磁化强度矢量的分布与理论模型很好吻合.（5）总之，利用井中曲线的水平分量、垂直分量和模量异常，能很好地反演总磁化强度大小和方向，这为计算和研究剩磁场、退磁场提供了一种有效方法.

4.2 组合模型

我们设计4种二维组合模型，分别是平行的板状体、向斜模型、断层切割模型和深度歼灭再现模型（如图3）.这4组模型的有效磁化强度M＝100000×10－3A/m，有效磁化倾角均为I＝45°.在磁性体模型的左、右侧分别有两个垂直钻孔ZK1和ZK2，井深均为500 m.井中水平分量、垂直分量和模量异常如图3中的红色、绿色和蓝色实线.

反演结果如图3所示，反演结果说明：（1）不同模型的水平分量、垂直分量和模量的观测曲线与预测曲线均很好拟合，算法收敛稳定.（2）用ZK1、ZK2磁异常的模量反演磁化强度大小的分布，反演的分辨率高，边界清楚，与理论模型一致，反演的效果好.（3）反演得到的磁化强度倾角的分布与外加磁场吻合，对磁化强度方向反演的效果好.综合磁化强度大小和方向的反演结果，磁化强度矢量的分布与真实模型一致.（4）井中磁测反演的另一个优点是反演的纵向分辨率高.如图3c、3d所示，断层切割模型和深度歼灭再现模型的反演结果在深度方向上的磁性变化均能清晰的反映，井中磁测反演能区分不同深度的两个磁性体，反演的纵向分辨率高.而地面磁测无法区分不同深度的两个磁性体，它在深度方向上的分辨率低，对磁性体下延深度的判断不准确.（5）计算出总磁化强度分布后，可以进一步计算和研究剩磁和退磁作用的影响.

5 强磁性体的退磁作用

5.1 退磁作用对磁异常的影响

图4是不同磁化率（κ＝0.01、0.1、1.0、10.0SI）圆柱体模型地面ΔT磁异常计算结果.图4中点划线1为根据重磁位泊松公式按圆柱体均匀磁化的磁场计算结果，没有考虑退磁作用的影响；实线2为有限元法磁场数值计算结果，考虑退磁作用的影响；虚线3为经过退磁系数退磁改正的磁场计算结果，考虑退磁作用的影响.其中圆柱体退磁系数为N＝0.5SI.对比图4中各异常曲线，可以得出：（1）当圆柱体磁化率κ＝0.01、0.1SI时，1、2、3线三者相互吻合；（2）但是当圆柱体磁化率达到κ＝1.0、10.0SI时，2、3线两者是相互吻合的，而与1线不吻合，表现为2、3线比1线幅值要小，且随着磁化率的增大，它们之间的偏差也越来越大.由此可以说明：重磁位泊松公式是以磁性体被均匀磁化为前提的，没有考虑到磁性体退磁作用.考虑退磁作用的异常幅值比不考虑退磁作用异常幅值要小，且随着磁化率的增大，它们之间的偏差越来越大.

表1表明，（1）当磁化率κ≤0.01SI时，相对偏差≤0.5%，磁场平均值、极大值的绝对偏差≤1nT，此时可以忽略退磁作用的影响；（2）当磁化率κ≤0.1SI时，相对偏差≤5%，磁场平均值绝对偏差≤6nT，极大值绝对偏差≤20nT，此时退磁作用的影响存在，但较弱；（3）当磁化率κ≥1.0SI时，相对偏差≥30%，磁场平均值绝对偏差≥400nT，极大值绝对偏差≥1300nT，此时退磁作用的影响很强；

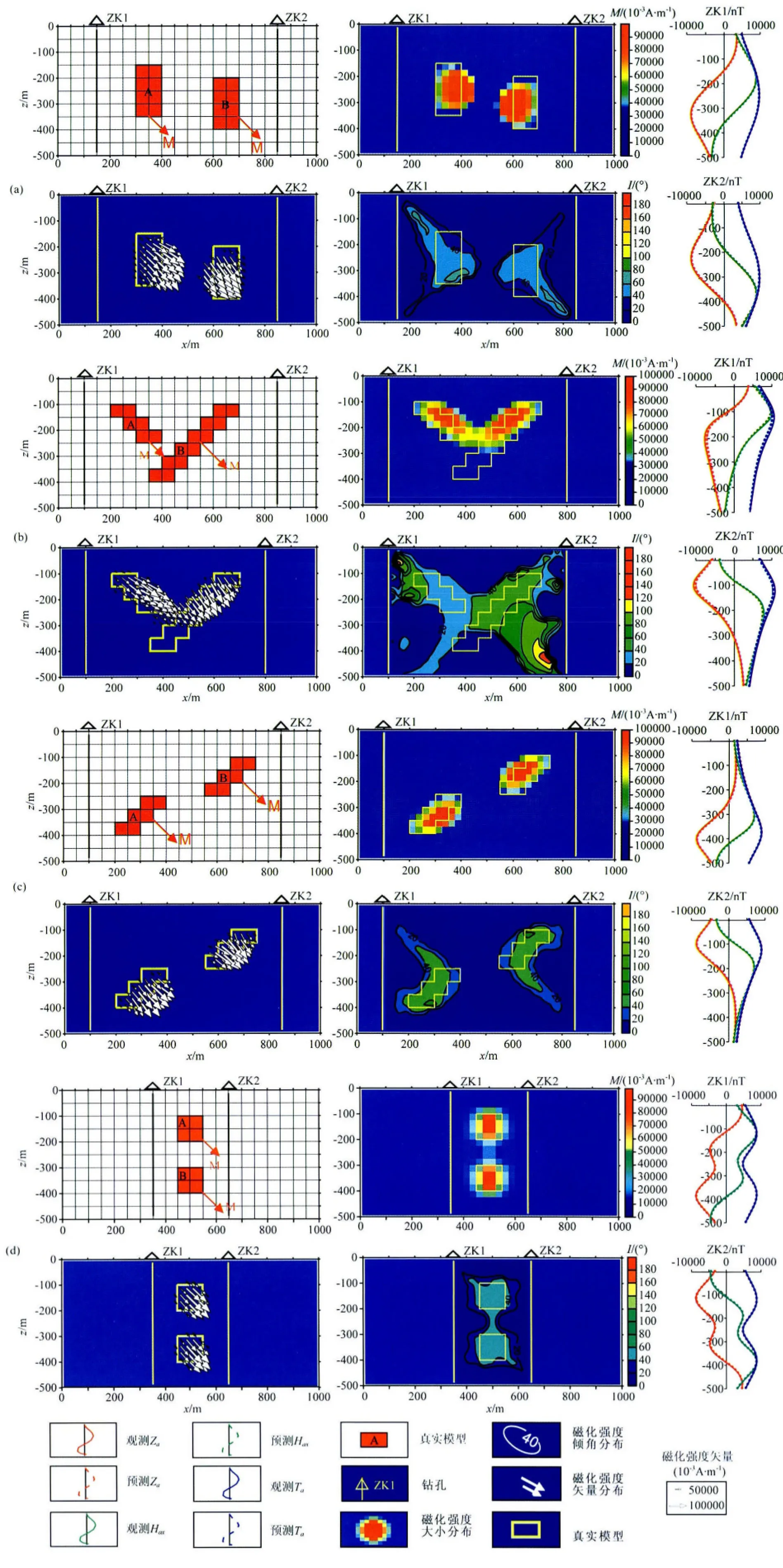
图3 二维组合板状体模型的井中磁测磁化强度矢量的反演结果Fig.3 Magnetization vector inversion results for borehole magnetic data of 2D combination dike prisms

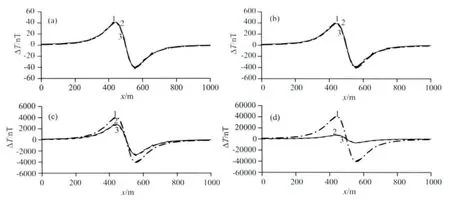
图4 退磁作用对磁异常的影响Fig.4 Effects of demagnetization to magnetic anomalies

（4）当磁化率κ≥10.0SI时，相对偏差≥80%，磁场平均值绝对偏差≥9900nT，极大值绝对偏差≥33000nT，此时退磁作用导致异常衰减很大.

5.2 表面磁荷密度分布特征

图5 板状体各边磁荷面密度分布Fig.5 Surface magnetic monopoles density distributions on dike′s sides

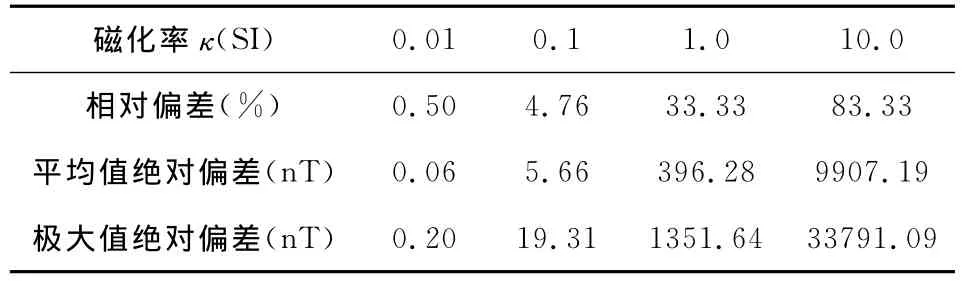
表1 考虑退磁作用与不考虑退磁作用异常幅值的偏差Table 1 Deviations of anomaly amplitudes considering demagnetization or not

图5a、5b分别是磁化率κ＝0.01SI和κ＝1.0SI板状体模型（图6）沿其边界一周AB→BC→CD→DA的磁荷面密度分布，正常地磁场强度B0＝50000nT.根据磁荷密度分布可以得出：（1）当κ＝0.01SI、1.0SI时，AB、BC边分布正磁荷，CD、DA 边分布负磁荷.（2）当κ＝0.01SI时，板状体各边AB、BC、CD、DA磁荷面密度曲线是水平直线，说明此时磁荷均匀分布.而当κ＝1.0SI时，板状体各边AB、BC、CD、DA磁荷面密度曲线不再是直线，说明此时磁荷分布不是均匀的，B点和D点磁荷密度最大，A点和C点磁荷密度最小.该现象说明，随着磁性体磁化率的增大，退磁作用的影响也越来越大，使得磁性体表面的磁荷分布不均匀，因而影响磁异常特征.

5.3 内部磁化强度分布特征

图6a、6b分别是磁化率κ＝0.01SI和κ＝1.0SI板状体模型内部总磁化强度大小分布，正常地磁场强度B0＝50000nT.根据其分布可以得出：（1）当κ＝0.01SI时，板体内部磁化强度的分布范围是（394～397.5）×10－3A/m，极大值与极小值之差只有3.5×10－3A/m，板体基本接近均匀磁化.当B0＝50000nT时，κ＝0.01SI磁性体按均匀磁化计算得到磁化强度M＝κB0/μ0＝397.89×10－3A/m.说明弱磁性板体内部磁化强度接近均匀磁化.（2）当κ＝1.0SI时，板体内部磁化强度的分布范围是（20000～33000）×10－3A/m，极大值与极小值之差达13000×10－3A/m，板体不再被均匀磁化，B、D点磁化强度最大，A、C点磁化强度最小.当B0＝50000nT时，κ＝1.0SI磁性体按均匀磁化计算得到磁化强度M＝κB0/μ0＝39788.74×10－3A/m.说明此时在退磁影响下，强磁性板状体内部磁化强度不再被均匀磁化，磁化强度比忽略退磁影响时要小.（3）综上，若磁性体磁化率越大，退磁作用的影响就越强，将导致磁性体内部磁化强度不再是均匀分布，且磁化率越大，这种不均匀性就越强，且板体内部磁化强度比不考虑退磁作用时要小，进而导致退磁作用下磁场幅值偏小.

图6c、6d分别是磁化率κ＝0.01SI和κ＝1.0SI板状体模型被磁化时内部总磁化强度倾角分布，正常地磁场强度B0＝50000nT，地磁倾角I0＝45°.根据其分布可以得出：（1）当κ＝0.01SI时，板体内部磁化强度倾角的分布范围是44.8°～45.25°，平均约45.05°，比地磁场倾角45°略大，极大值与极小值之差约0.45°，磁化方向基本没有变化.说明弱磁性板体内部磁化强度倾角基本没有变化.（2）当κ＝1.0SI时，板体内部磁化强度倾角的分布范围是30°～58°，平均约50°，比地磁场强度倾角45°要大5°，其极大值与极小值之差达28°，板体内部磁化强度不再均匀，B、D点磁化强度最大，A、C点磁化强度最小.说明此时在退磁影响下，强磁性板状体内部不再被均匀磁化，磁化强度方向往长轴方向偏转.（3）若磁性体磁化率越大或磁性体厚度越薄，总磁化强度倾角往长轴方向的偏转就越大（如图7）.

6 理论模拟：高磁化率磁性体井中磁测反演

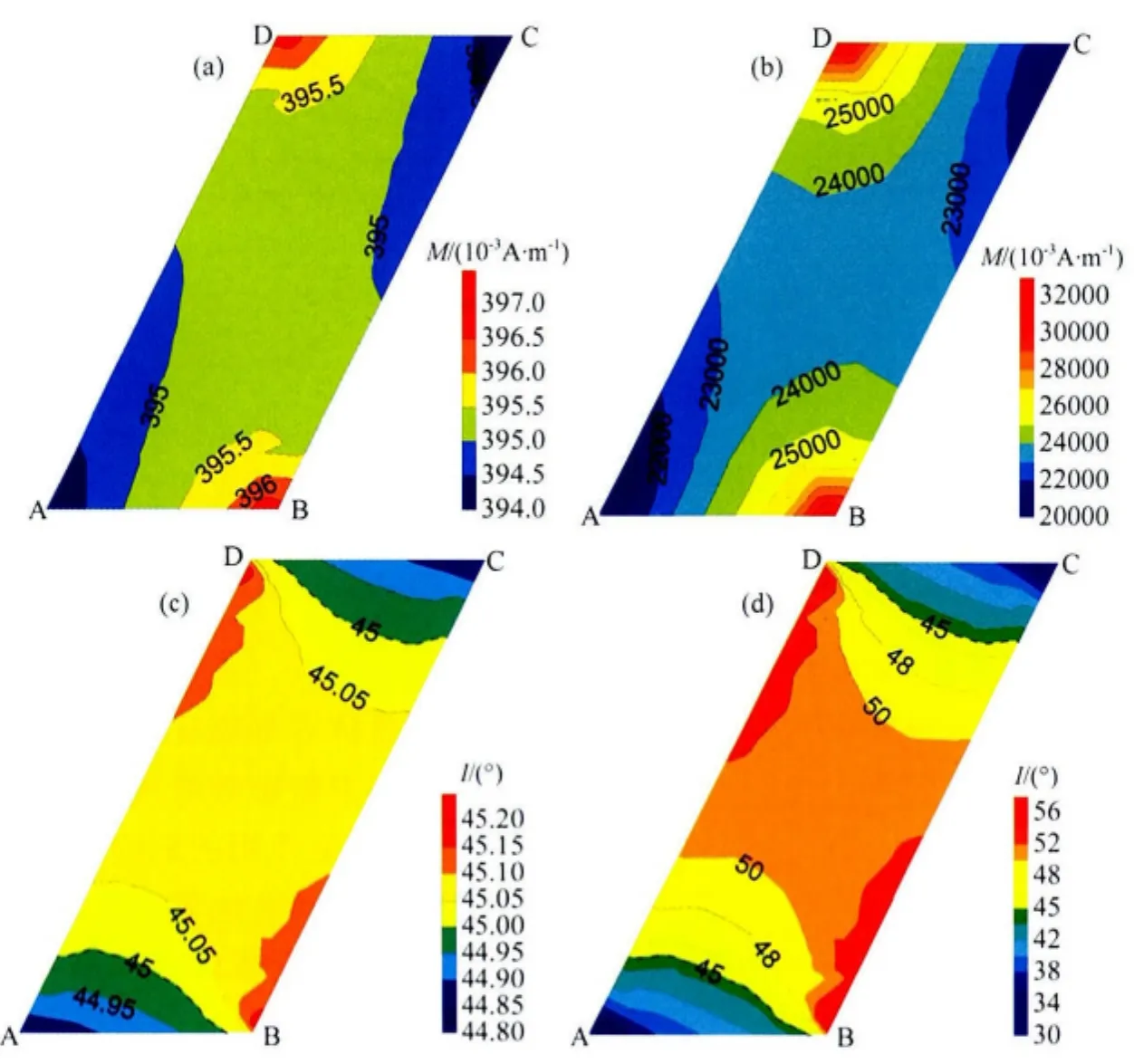
图6 板状体内部磁化强度大小和倾角的分布Fig.6 Distributions of magnetization intensity and inclination in dike

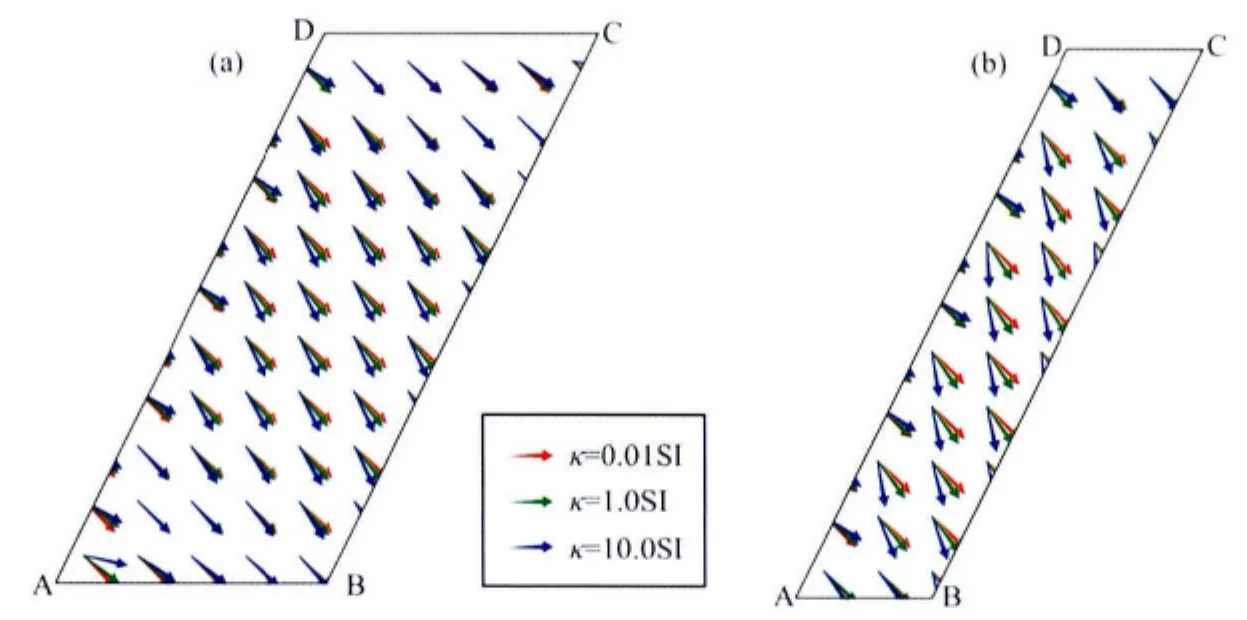
图7 退磁作用对板状体内部磁化强度方向的影响Fig.7 Influence of demagnetization to magnetization inclination in dike

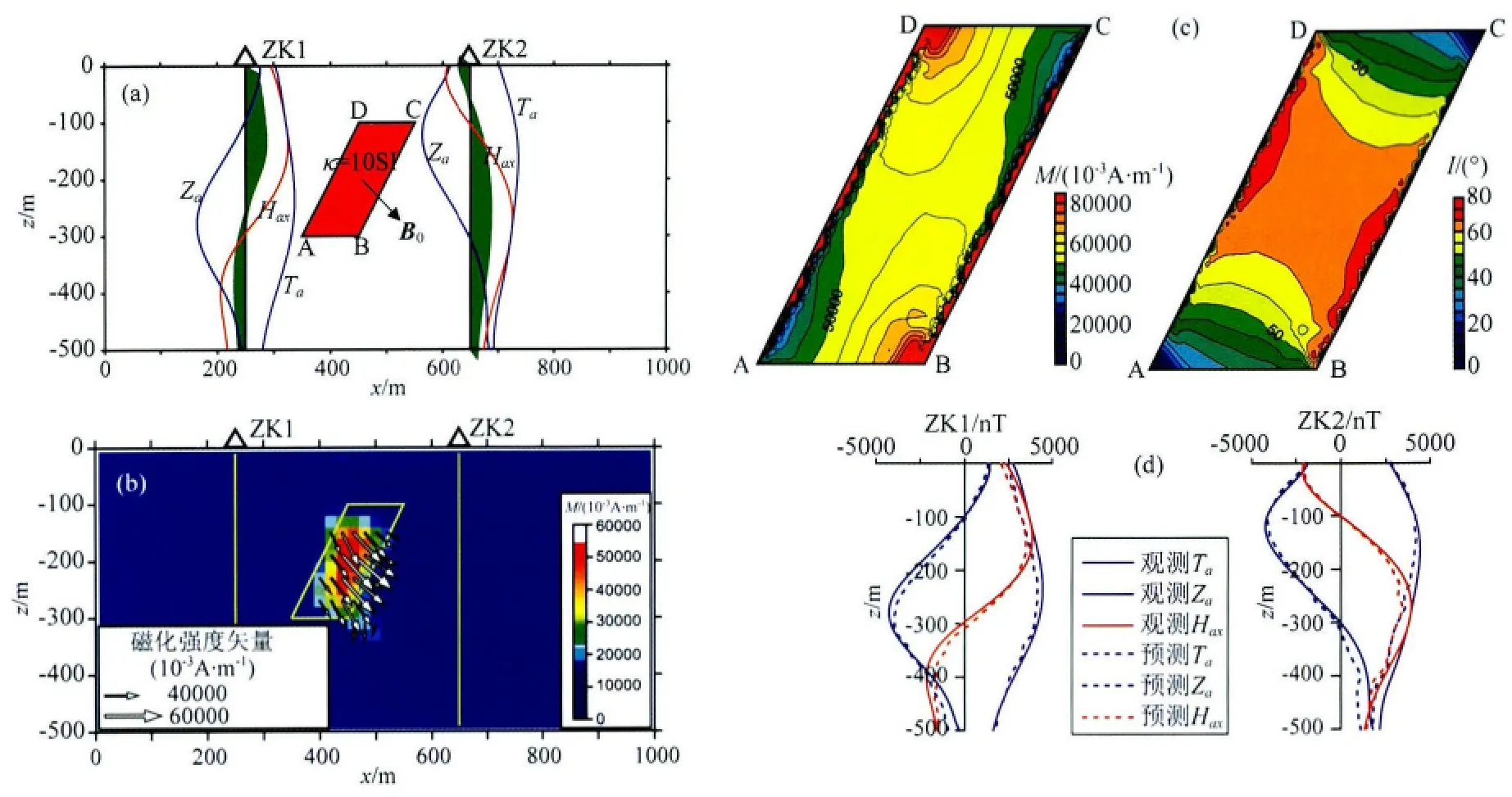
图8 强磁性板状体模型的磁化强度矢量反演结果Fig.8 Magnetization vector inversion results of a synthetic dike with high susceptibility

如图8所示，设一二度板状体模型，四个角点的坐标为 A（350m，－300m），B（450m，－300m），C（550m，－100m），D（450m，－100m）.板状体具有很强磁性，磁化率κ＝10.0SI，正常地磁场强度B0＝50000nT，地磁场倾角为I0＝45°，剖面正南北走向.在剖面的左右两侧有垂直钻孔ZK1和ZK2，钻孔深度500m，ZK1和ZK2的水平分量异常Hax、垂直分量异常Za和模量异常Ta如图8a所示.图8b是ZK1和ZK2井中磁测的磁化强度大小和方向的反演结果.由图可知：（1）预测数据能很好地拟合观测数据（图8d），反演过程稳定收敛.（2）反演的磁化强度大小分布分辨率高，磁性边界清晰，与理论板状体的位置吻合.（3）反演磁化强度的大小的范围是（30000～58867）×10－3A/m，平 均 值 为50000×10－3A/m，与有限元法模拟的强磁性体在退磁作用影响下的板状体内部磁化强度分布一致.如图8c所示，在均匀外磁场B0作用下，强磁性板状体不是被均匀磁化，其内部磁化强度分布不均匀，磁化强度大小的范围是（50000～60000）×10－3A/m，这一值比不考虑退磁作用影响计算的板状体内部磁化强度M＝κB0/μ0＝397887.4×10－3A/m 小1/7，退磁作用对强磁性体内部磁化强度影响很大.（4）如图9所示，显示了（30000～60000）×10－3A/m磁化强度大小范围内的磁化强度倾角结果.磁化强度倾角的变化范围是45°～70°，平均值为56°，与有限元法模拟的退磁作用影响下的板状体内部磁化强度倾角分布吻合.如图8c所示，有限元模拟磁化倾角的范围是50°～65°，平均值为60°，退磁作用使板状体内部磁化强度方向往长轴方向偏转约15°.（5）综合之，反演得到的内部磁化强度矢量的分布与实际情况退磁作用下板状体内部磁化强度矢量的分布是一致的，说明该方法反演磁化强度矢量的有效性.因而，该方法可以用于研究剩磁、退磁情况下的总磁化强度大小和方向的分布.

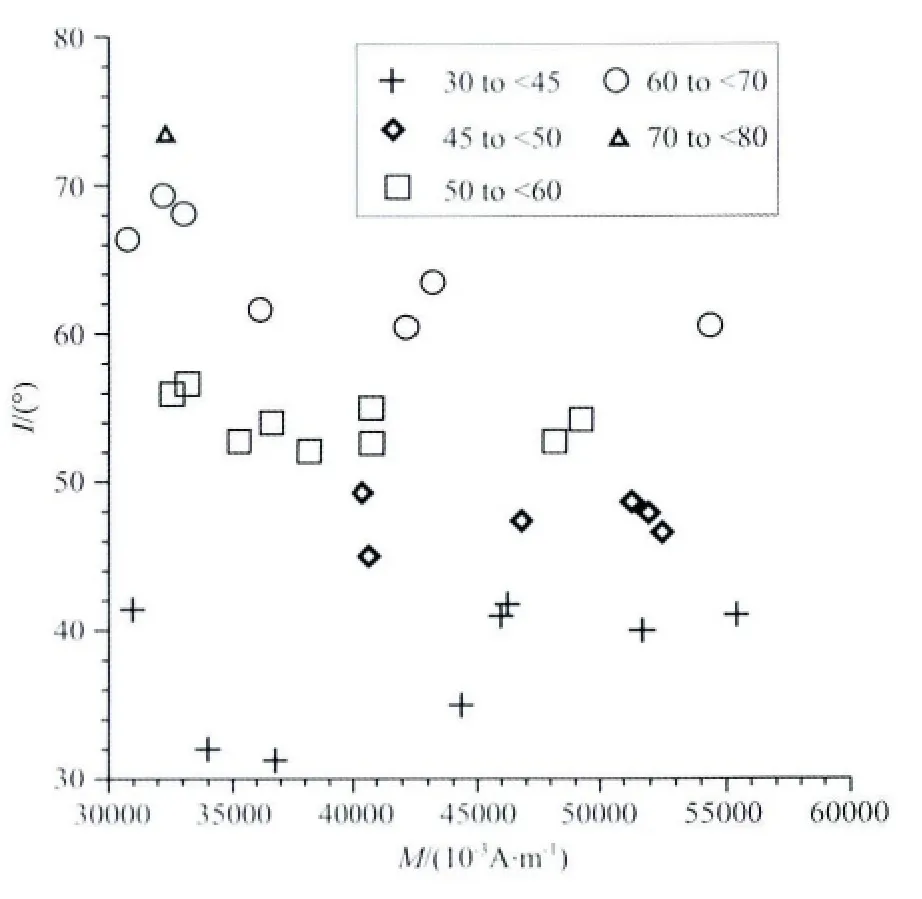
图9 强磁性板状体模型磁化强度倾角的反演结果Fig.9 Inversion results of magnetization inclination of a synthetic dike with high susceptibility

7 结 论

利用井中磁测的磁异常模量弱敏感于磁化方向的特点，首先计算磁化强度大小的分布；然后利用其相位信息，拟合磁场分量异常，计算得到磁化强度方向的分布.该方法能准确地获得总磁化强度大小和方向，可应用于剩磁和退磁的计算和研究.井中磁测是矢量信息，本身所含的信息量比地面磁测丰富，如果能充分利用，它将在确定深部隐伏矿体的方位、深度、总磁化强度大小和方向方面起重要作用.相比地面磁测，井中磁测的不足之处在于，由于受孔位的约束，限制了井中磁测数据的采集.如果能全方位采集井中磁测数据，将对磁性体的全空间约束起重要作用.

（References）

［1］ 刘双，刘天佑，高文利等.退磁作用对磁测资料解释的影响.物探与化探，2012，36（4）：602－606.Liu S，Liu T Y，Gao W L，et al.The influence of demagnetization on magnetic data interpretation.Geophys.Geochem.Explor.（in Chinese），2012，36（4）：602－606.

［2］ Guo W W，Dentith M C，Bird R T，et al.Systematic error analysis of demagnetization and implications for magnetic interpretation.Geophysics，2001，66（2）：562－570.

［3］ Guo W W，Dentith M C，Li Z，et al.Self demagnetisation corrections in magnetic modelling：some examples.Explor.Geophys.，1998，29（4）：396－401.

［4］ Purss M B J，Cull J P.A new iterative method for computing the magnetic field at high magnetic susceptibilities.Geophysics，2005，70（5）：L53－L62.

［5］ Wang M Y，Di Q Y.Magnetization vector tomography.CT Theory and Appl.，2000，9（Suppl.）：48－50.

［6］ 王妙月，底青云，许琨等.磁化强度矢量反演方程及二维模型正反演研究.地球物理学报，2004，47（3）：528－534.Wang M Y，Di Q Y，Xu K，et al.Magnetization vector inversion equation and 2D forward and inversed method study.Chinese J.Geophys.（in Chinese），2004，47（3）：528－534.

［7］ Dannemiller N，Li Y.A new method for determination of magnetization direction.Geophysics，2006，71（6）：L69－L73.

［8］ Shearer S，Li Y.3D Inversion of magnetic total gradient data in the presence of remanent magnetization.SEG Annual Meeting，2004.

［9］ Krahenbuhl R A，Li Y.Influence of self－demagnetization effect on data interpretation in strongly magnetic environments.ASEG Extended Abstracts，2007，（1）：1－4.

［10］ Lelièvre P G，Oldenburg D W.A 3D total magnetization inversion applicable when significant，complicated remanence is present.Geophysics，2009，74（3）：L21－L30.

［11］ Lelièvre P G，Oldenburg D W，Phillips N G.3D magnetic inversion for total magnetization in areas with complicated remanence.SEG Annual Meeting，2006.

［12］ Lelièvre P G，Oldenburg D W.Magnetic forward modelling and inversion for high susceptibility.Geophys.J.Int.，2006，166（1）：76－90.

［13］ 陶德益，杨海燕，肖明尧等.井中磁测在大冶铁矿深部勘查中的应用效果.资源环境与工程，2011，25（4）：358－363.Tao D Y，Yang H Y，Xiao M Y，et al.The application effect of borehole magnetic exploration in the prospecting of the Daye iron mine.Resour.Envi.Eng.（in Chinese），2011，25（4）：358－363.

［14］ 颜廷杰，朱谷昌.井中磁测在矿区找矿中的应用效果及经验.矿产勘查，2011，2（6）：789－794.Yan T J，Zhu G C.The application and lessons of borehole magnetic survey in mining areas.Miner.Explor.（in Chinese），2011，2（6）：789－794.

［15］ 杨坤彪，陶德益，范新省.利用井中磁方位异常判断磁性体位置的方法.物探与化探，2010，34（6）：717－721.Yang K B，Tao D Y，Fan X S.The application of the magnetic azimuth anomaly method to determining the location of a magnetic body.Geophys.Geochem.Explor.（in Chinese），2010，34（6）：717－721.

［16］ Li Y G，Oldenburg D W.Joint inversion of surface and threecomponent borehole magnetic data.Geophysics，2000，65（2）：540－552.

［17］ 刘双，张大莲，刘天佑等.井地磁测资料联合反演及应用.地质与勘探，2008，44（6）：69－72.Liu S，Zhang D L，Liu T Y，et al.Cooperative inversion and application of surface and borehole magnetic data.Geol.＆Prosp.（in Chinese），2008，44（6）：69－72.

［18］ 习宇飞，刘天佑，刘双.井中磁测三分量联合反演.石油地球物理勘探，2012，47（2）：344－352.Xi Y F，Liu T Y，Liu S.A joint inversion method for borehole magnetic three－component data.Oil Geophys.Prosp.（in Chinese），2012，47（2）：344－352.

［19］ Gerovska D，Ehara S.Calculation of modulus T of the anomalous magnetic vector over Large Areas.Memoirs of the Faculty of Engineering Kyushu University，2002，62（4）：139－148.

［20］ Stavrev P，Gerovska D.Magnetic field transforms with low sensitivity to the direction of source magnetization and high centricity.Geophys.Prosp.，2000，48（2）：317－340.

［21］ Gerovska D，Araúzo－Bravo M J.Calculation of magnitude magnetic transforms with high centricity and low dependence on the magnetization vector direction.Geophysics，2006，71（5）：121－130.

［22］ Gerovska D，Araúzo－Bravo M J，Stavrev P.Determination of the parameters of compact ferro－metallic objects with transforms of magnitude magnetic anomalies.J.Appl.Geophys.，2004，55（3－4）：173－186.

［23］ Gerovska D，Araúzo－Bravo M J，Stavrev P.Estimating the magnetization direction of sources from southeast Bulgaria through correlation between reduced－to－the－pole and total magnitude anomalies.Geophys.Prosp.，2009，57（4）：491－505.

［24］ Gerovska D，Stavrev P. Magnetic data analysis at low latitudes using magnitude transforms.Geophys.Prosp.，2006，54（1）：89－98.

［25］ Pilkington M.3－D magnetic imaging using conjugate gradients.Geophysics，1997，62（4）：1132－1142.

［26］ 吴小平，徐果明.利用共轭梯度法的电阻率三维反演研究.地球物理学报，2000，43（3）：420－427.Wu X P，Xu G M.Study on 3－D resistivity inversion using conjugate gradient method.Chinese J.Geophys.（in Chinese），2000，43（3）：420－427.

［27］ 胡祖志，胡祥云，何展翔.大地电磁非线性共轭梯度拟三维反演.地球物理学报，2006，49（4）：1226－1234.Hu Z Z，Hu X Y，He Z X.Pseudo－three－dimensional magnetotelluric inversion using nonlinear conjugate gradients.Chinese J.Geophys.（in Chinese），2006，49（4）：1226－1234.