数控机床电主轴热态特性分析

谢晨琳

（四川建筑职业技术学院机电与信息工程系，四川德阳 618000）

0 引言

由于数控机床电主轴系统零部件多、结构复杂，对其进行热分析时，需要大量数据，但是各零部件的温升与热变形数据通过实验很难获取，且工作量巨大。随着有限元分析方法的快速发展，为这一难题提供了解决思路。相关研究表明[1-2]，有限元分析法是一种对研究对象温度场分布进行分析的有效方法，可以通过仿真的方法获得温度场分布，并且可获得大量可靠数据，使热分析不再对实验数据具有较高的依赖性。为了解决数控机床电主轴系统热态特性分析过程中对实验数据的严重依赖问题，有必要对电主轴系统利用有限元分析方法进行热态特性分析。

1 有限元模型构建

有限元分析方法作为一种有效的数控机床电主轴热态特性分析方法，受到国内外学者的广泛使用，其基本思路[3]是将复杂的电主轴结构用三维软件进行建模，并导入有限元分析软件进行网格划分，对各部件的单元类型及材料属性进行定义；然后根据电主轴系统的热源及其产热原理计算主轴各部分发热量，加热载边界条件；最后得到温度场分析。其基本思路如图1所示。

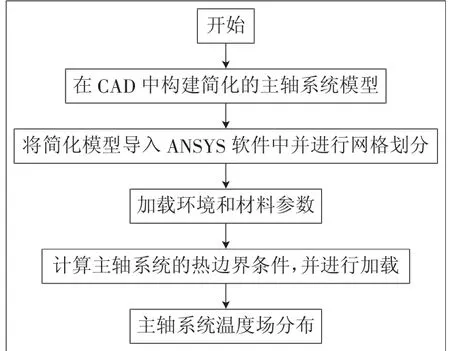
图1 电主轴系统热态特性分析流程图

1.1 电主轴有限元建模

由于电主轴系统是一个回转体，根据其结构特点可将其视为轴对称结构，为了简化建模过程和计算过程，在对电主轴进行热态特性分析时，选取电主轴的一半作为研究对象进行建模研究。为了对模型进行简化，可对主轴系统上的非关键部位进行简化处理，简化点主要包括：1）删除主轴系统中对主轴热态特性影响较小的零部件，如弹簧、螺钉等；2）去除主轴系统上对热态特性分析结果影响较小的无关特征，如：圆角、台阶、小孔等；3）忽略轴承内部结构。

1.2 网格划分与参数加载

为了获得主轴系统中各部位的具体热态特性，需要对主轴系统模型进行网格划分，网格数越多计算结果越精确，同时计算量也会增加，因此需要确定合适的网格尺寸及网格数量，在保证计算准确性的前提下尽量保证计算时间不会太长。扫掠法是有限元分析中一种较为常用的网格划分方法，其具有计算结果与实际结果符合率高的特点，且对于系统在加载后的计算过程有加快计算速度的作用，因此选用扫掠法对主轴系统进行网格划分。经过对网格尺寸的反复测试，发现当网格尺寸大于等于5 mm时，计算结果准确率较低，计算误差较大；当网格尺寸为3 mm和2 mm时，均能获得比较准确的计算结果，但当网格尺寸为2 mm时，网格数量是网格尺寸为3 mm时的1.5倍，意味着其计算量与计算时间是网格尺寸为3 mm时的1.5倍。为了保证计算结果准确性同时保证计算速度，将网格尺寸设置为3 mm，电主轴系统的网格划分如图2所示，其中节点数为632 541，单元数为302 546。

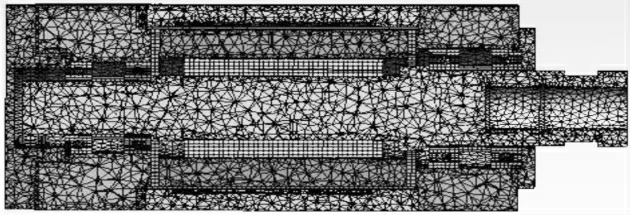
图2 电主轴网格划分

对主轴系统进行热态特性分析，需对主轴系统的运行环境参数及各零部件的材料属性进行定义，环境参数主要包括：环境温度、主轴转速、冷却液入口/出口温度、气压、冷却液流量。主轴系统运行的环境参数如表1所示。针对不同材料其材料属性不同，所研究电主轴系统中主轴材料为20Cr2MnMo，轴承滚动体材料为Si3N4，轴承内外圈为钢性材料，主轴系统零部件材料属性如表2所示。

表1 电主轴运行的环境参数

表2 电主轴各零部件的材料参数

2 电主轴系统热载荷计算

由于电主轴组成结构复杂，因此电主轴的传热机制也较为复杂。主轴系统的主要发热源为驱动电动机和滚动轴承，电动机的发热可以假定为电动机的功率损耗，轴承的发热量可通过公式进行计算。

2.1 电主轴产热量计算

五轴数控机床使用的是混合电主轴，电主轴主要结构包括：无刷电动机、高精度轴承、主轴冷却机构、锁刀和松刀机构、壳体等[4]。电主轴构造复杂、密封性好，主要发热源为驱动电动机定子、转子发热和前后轴承摩擦生热[5]，热量难以通过冷却系统完全散失，剩余的热量共同影响电主轴内部部件，传热过程可以简化为主轴冷却系统带走部分热量，剩余热量通过热传导传递到主轴上，最终影响到轴端位移，计算主轴发热量时，记电主轴的总残余热量为Q，电动机残余热量为Q1（t），轴承摩擦生热的残余热量为Q2。电主轴的总残余热量Q的计算公式为

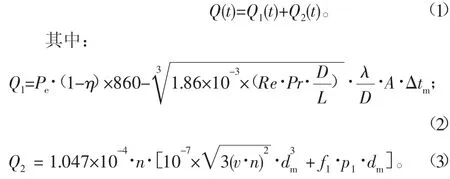
式中：Pe为电动机的额定功率；η为电动机的工作效率；Re为雷诺数；Pr为普朗特系数；D为冷却液管路的直径；L为冷却液管路的长度；A为冷却液为主轴系统散热的接触面积；Δtm为换热表面与流体的温差；n为主轴转速；dm为轴承平均直径；f1为与轴承类型和所受负荷有关的系数。

2.2 电主轴传热计算

电主轴传热过程主要包括：轴承与空气的对流换热、电动机与冷却水的对流换热、电动机转子的传热、电主轴前后密封环的对流换热、电主轴与空气的传热[6]。

1）轴承与空气的对流换热。由于轴承使用油气润滑的方式进行润滑，润滑油的量较小且润滑油的主要作用是实现轴承滚动体与内外圈之间的润滑，因此润滑油所带走的轴承热量较少，与其他传热方式相比可忽略不计。轴承与空气之间的对流换热作为轴承主要的散热方式，其带走了轴承大部分热量，在电主轴运行过程中，压缩空气朝轴承喷气，冷空气沿轴承的轴向快速流动，使轴承与空气之间发生强迫对流换热，该气流与轴承的接触面积为

2）电动机与冷却液的对流换热。在电动机运动过程中，会有冷却系统对电动机系统进行持续冷却，由于不同冷却液的冷却效果不一样，且冷却液的流体状态也会对换热规律及传热效果产生影响，因此必须对冷却液的雷诺数Re进行计算，以判定冷却液的流态是层流还是紊流，当雷诺数小于2200时为层流，大于2200时为紊流[7]，其计算公式为

式中：v为冷却液流速，m/s；γ为冷却液的运动黏度，m2/s；D为冷却液管路的几何定型尺寸，m。

冷却液管路的几何定型尺寸的计算公式为

式中：Ref为参考温度下的雷诺数；Prf为参考温度下的普朗多准数；vf为参考温度下的运动黏度；vw为实际运动黏度。

3）电动机转子的传热。电动机转子的运动环境较为复杂，因此其热量传递的形式多样，较为繁杂。其中最主要的传热形式包括电动机转子往主轴上的传热、往转轴和轴承上的传热及往空气中的传热。当转子气隙的Re小于2200的情况下，气体处于纯层流状态，主要传热方式为热传导，此时转速对传热量的影响可忽略不计，传热量受主轴材料及自身传导系数的影响。转子与空气之间的对流换热系数的计算公式为

式中，u为单位时间内气体流过的距离，m/s。

当电主轴系统有轴向通气时，对流换热系数受转子自转所产生的周向气流和轴向通气系统提供的轴向气流的共同影响，因此，此时转子的单位时间内气体流过的距离为

式中：Nu为努赛尔数；λ为流体导热系数，W/(m·K)；H为气隙尺寸，m；δ为定子与转子之间的平均距离，m；r1为转子外表面半径，m。

4）电主轴前、后密封环的对流换热系数。在电主轴运行过程中，电主轴前后密封环由于有气隙的存在且有空气流动，因此沿电主轴轴向运动的气体会带走部分热量，此时的努赛尔系数可通过下式进行计算：

式中，γ1为密封环气隙的平均半径，m。

进而求出此时的对流换热系数为

5）高速电主轴与外部空气的传热。电主轴运行时，主轴温度升高，环境温度始终保持在20 ℃，由此形成温度差，由于有温度差的存在，就会产生热对流，因此，主轴的热量会往空气中传递。假设主轴与环境空气之间的热传递是通过自然的热对流换热形式进行，可以将对流换热系数取为α=9.7 W/（m·℃）。

3 电主轴热态特性分析

将上述热量计算作为有限元分析的边界条件加载到主轴系统模型中，得到主轴系统稳态温度场分布图，如图3所示。由主轴系统稳态温度场分布图可以看出，电主轴的最高温度为56.71 ℃，位于电主轴的转子铁芯处；第二温度梯度的温度为53.945 ℃，位于电主轴的定子处。分析其原因可能是因为主轴系统由主轴箱进行封闭，转子在高速转动的过程中产生热量，没有冷却系统对其进行直接冷却，只能通过热传导及热对流的方式散热，散热条件较差，热量不能及时散发出去，因此电主轴的转子温度较高；在电主轴运行过程中，定子在各种因素的综合作用下也会产生大量热量，且其产生的热量不低于转子所产生的热量，但由于定子有固定的冷却系统对其进行降温，及时带走定子上的热量，从而使定子的温度低于转子的温度。

图3 主轴系统稳态温度场分布

4 结论

通过对电主轴系统进行建模并利用ANSYS软件进行网格划分、参数加载及边界条件的计算和加载，最终获得电主轴稳态温度场分布图，发现电主轴系统中转子和定子是发热最严重的地方，并对其产生的原因进行了分析，可为数控机床电主轴的温度控制及热分析提供理论基础和数据支撑。