一道平面向量问题引发的思考与探究

陈 芳

(山东省桓台第二中学 256400)

数学家哈尔莫斯所说：“数学的真正组成部分是问题和解”.作为高中数学老师，在教学中要重视学生出现的错误问题，深入研究学生出现问题的本源，抓住错误症结，总结规律，找出本质，最终形成解决这类问题的通性通法，要把学生在解题过程中出现的错误看成是认识学生思维规律的重要手段，最终实现教学相长.

在一堂平面向量习题课中，学生在讲解一道平面向量问题时，出现了几种具有代表性的错误解法，引起我的注意和兴趣，通过探究，挖掘出学生在解决向量问题中出现的一些共性问题，并给出了两种常见的处理方法.

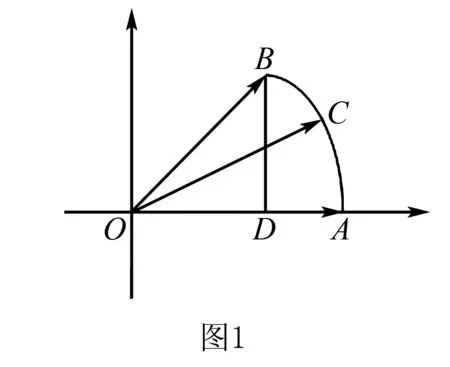
一、引例

二、三种典型的错误解法

错因辨析在不等式问题中，有不少同学习惯将两个不等式相加，得出取值范围，殊不知在没有探究题设条件范围时，就将不等式相加或者相减，容易引起结果范围的扩大或缩小，因此要告诫学生审题和分析题设条件是解对问题的关键和前提.

此题就是个别学生忽视了题设条件中，点的横、纵坐标之间有制约关系，将两个不等式直接相加，结果扩大了.

x2+y2+xy=1，令t=x+2y，

∴x=t-2y代入上式整理得

3y2-3ty+t2-1=0有解，

∴Δ≥0，解得-2≤t≤2∴x+2y的最大值是2

错因辨析个别学生将这道最值问题，通过换元转化为二次函数方程有解，想法很巧妙，答案对，但比较遗憾的是学生忽略了y的条件限制.

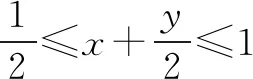
①

②

三、两种巧妙的解法

高中阶段涉及求最值问题，通常有四种方法，转化为二次函数求最值、基本不等式、求导和三角函数的方法，鉴于此，解法一通过寻求等式中x，y的关系，转化为给定区间上二次函数求最值，解法二是通过数形结合，将问题转化成三角型函数y=Asin(ωx+φ)，进而在指定的区间上求出最值.

两边平方，化简得：x2+y2+xy=1，

令t=x+2y，t2=x2+4xy+4y2=x2+4(xy+y2)=x2+4(1-x2)=4-3x2.

又0≤x≤1，由二次函数的知识得：1≤t2≤4，

即1≤x+2y≤2，∴x+2y的最大值是2

点评通过将向量等式两边平方，转化成代数式，再对t=x+2y平方后代入消元，最后利用给定区间上的二次函数，求出最值.

∴x+2y的最大值是2.

点评在高中解决平面向量的问题中，建立直角坐标系是一种常用的方法.因此建好直角坐标系后，将向量式转化成三角函数形式，最终借助三角型函数得解.

在高中数学教学中，教师要注重对试题命制立足点的溯源.本题考察了向量与最值之间的关系，如何由向量式转化成代数式，最后借助二次函数和三角函数求出最值是学生需要深思的地方.

教学中应该借助此题进行总结平面向量最值问题，一是向量式转化成代数式的两种常见方法建系坐标化和数量积(平方是一种常用手段)，二是求最值的常见几种方法.在教学中引导学生经常反思，可以从不同的角度得到同一道题的多种解法，能使学生在无数的表象下面牢牢抓住数学的本质，从而使学生的解题能力得到不断升华和提高.