证据推理模型认知 知识能力全面考察Ka计算
——“直线方程法”巧解全国乙卷第13题
2021-08-19刘春凯
刘春凯
(天津市新华中学 300204)
【2021全国乙卷第13题】 HA是一元弱酸,难溶盐MA的饱和溶液中c(M+)随c(H+)而变化,M+不发生水解.实验发现,298K时c2(M+)-c(H+)为线性关系,如图1中实线所示:

图1
下列叙述错误的是( ).
A.溶液pH=4时,c(M+)<3.0×10-4mol·L-1
B.MA的溶度积Ksp(MA)=5.0×10-8
C.溶液pH=7时,c(M+)+c(H+)=c(A-)+c(OH-)
D.HA的电离常数Ka(HA)≈2.0×10-4
首先要观察这个题的题干,横纵坐标含义(注意横坐标数量级是10-5,纵坐标数量级是10-8),曲线变化趋势,曲线上的特殊点.结合溶度积常数,弱电解质电离常数,盐类的水解等知识储备,考察了理解与辨析,分析与推测,归纳与论证的关键能力,考察非常全面,立意鲜明,素养为本,渗透科学方法,突出能力全面考察.
通过分析,可以培养学生构建图2所示的思维方式,突出学科的核心素养3证据推理与模型认知:

图2
解题技巧对于本题难溶物MA溶度积Ksp的求法,可以用特殊点横坐标为0点,可溶液中c(H+)怎么可能为0呢? 这只是曲线外推的一种极限结果,所以在直线接近纵坐标截距部分画成了虚线,体现了非常好的科学性,也是本题的亮点,此时c(M+)=c(A-),截距c2(M+)正好对应MA的溶度积常数,故Ksp(MA)=5.0×10-8,B项正确;
当横坐标为10,表示c(H+)=10×10-5,即pH=4时,纵坐标c2(M+)=7.5×10-8,c(M+)<3.0×10-4mol·L-1,A项正确;
对于C选项,MA饱和溶液,电荷守恒c(M+)+c(H+)=c(A-)+c(OH-)必然成立,此时A-会水解,溶液成碱性pH>7, 要变成C选项pH=7,c(OH-)减小,c(H+)就要增大,根据图像c2(M+)也随之线性增大,根据溶度积常数c(M+)增大,则c(A-)就会减小,则电荷守恒等式两边离子浓度变化趋势如下:
c(M+)↑+c(H+) ↑=c(A-)↓+c(OH-)↓
为了维持电荷守恒,等式右侧必须存在其他阴离子,所以加入的酸可能是盐酸等其他酸而不是HA,这样符合新的电荷守恒c(M+)+c(H+)=c(A-)+c(OH-)+c(Cl-),所以C选项错误.这就是信息获取,证据推理,分析推测等一系列思维,这也是新课程改革特别需要培养的学生能力.
对于D选项Ka的计算也是本题的亮点,提供两种解法以供参考:
解法一平衡计算

c(HA) =2.74×10-4-1.82×10-4=0.92×10-4
=2×10-4
这种方法化学原理简单,但是在考试过程中计算量很大,而且要开根号,学生不太容易完成,那么能否根据题目中直线方程找到关键的函数关系呢?
解法二直线方程法
根据直线方程y=aX+b,很容易求出直线斜率a=2.5×10-4和截距b=5×10-8,得直线方程
y=2.5×10-4x+5×10-8
即c2(M+)=2.5×10-4c(H+)+5×10-8

Ksp(MA)=c(M+)×c(A-) ②
物料守恒c(M+)=c(HA)+c(A-) ③
为了得到c2(M+),等式③两边都乘以c(M+),得
c2(M+)=c(M+)c(HA)+c(M+)c(A-)
根据等式②得
c2(M+)=c(M+)c(HA)+Ksp(MA)④
根据等式①
带入④得
这便是证据推理.
对比前面直线方程可以发现斜率为
带入Ksp(MA)=5.0×10-8
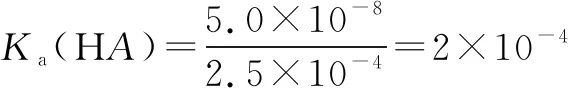
利用这种直线方程法巧解Ka计算,事半功倍,计算量很小,特别适合综合能力突出的考生,试题区分度很大,亮点很多,需要多加练习培养学生证据推理与模型认知的核心素养.此题是一道不可多得的好题,把化学原理本质内容用数学形式表现出来,立意鲜明,素养为本,情景基于实际问题,渗透科学方法,设问指向集中,突出关键能力考察,通过分析提高高考解题能力,充分备战新高考.
