高考中应用题瓶颈突破——以江苏高考应用题为例

尤蓓君

(江苏省南菁高级中学 214400)

应用题是用语言或文字叙述有关事实，反映某种数学关系，并求解未知数量的题目，每道应用题都包括已知条件和所求问题.在数学高考中，应用题不仅是一个常设题型，还占据着较大的分值比例，学生虽然从小学阶段就开始接触应用题，不过高考中的应用题难度系数较大，教师需指导他们从具体的逻辑思维出发，使其认真分析题目内容，真正突破瓶颈.

一、高度重视审题环节，做好应用题解题准备

高考数学应用题涉及题材广泛，背景也呈现出多样的色彩，一般情况下，文字叙述较长，数据多、不规则，文字、符号及其相关关系式相互交织，显得复杂、繁琐.要想突破高考中数学应用题的瓶颈，教师首先需要求学生高度重视审题环节，认真阅读题目信息，细致、耐心的审题，使其学会去粗取精，抓住题目的主干，同时挖掘出隐含条件，做好准备工作.

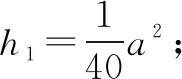
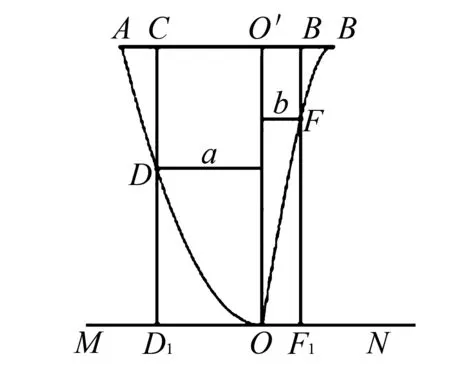
图1

(1)求桥AB的长度；

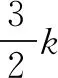
教师引领学生仔细阅读题，使其找出关键信息、已知与未知条件，弄懂文字与符号的含义，做好解题准备.

二、识别实际问题模式，确定应用题解题思路

应用题本身反映的就是实际生活中的相关事实，针对高考数学应用题中的瓶颈而言，教师需引领学生对实际问题的模式进行识别.

例2如图2，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l，湖上有桥AB(AB是圆O的直径).规划在公路l上选两个点P、Q，并修建两段直线型道路PB、QA.规划要求：线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足)，测得AB=10，AC=6，BD=12(单位：百米).

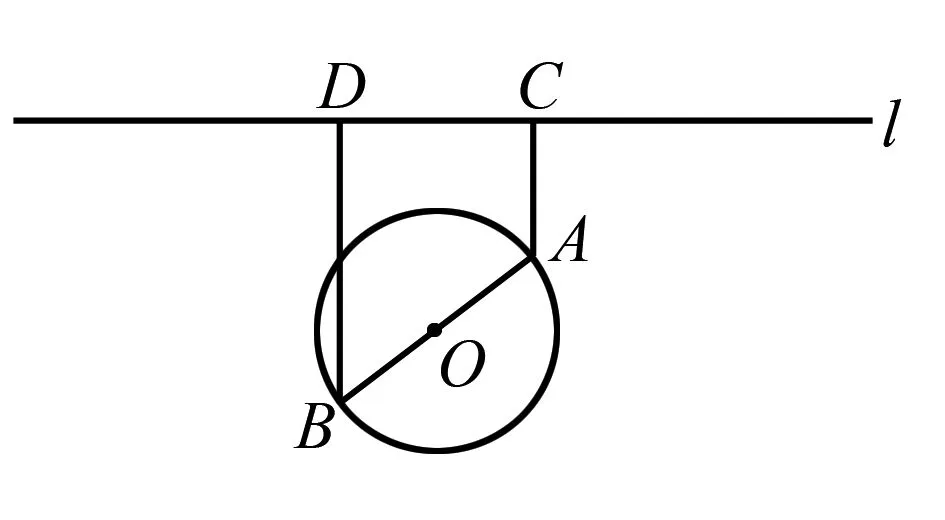
图2

(1)若道路PB与桥AB垂直，求道路PB的长；

(2)在规划要求下，P和Q中能否有一个点选在D处？并说明理由；

(3)对规划要求下，若道路PB和QA的长度均为d(单位：百米).求当d最小时，P、Q两点间的距离.

本题属于典型的测量题，教师引领学生联系到三角函数的知识，并结合圆、平面直角坐标系、斜率、两点距离公式等确定思路，让他们顺利解题.

三、运用数形结合思想，优化应用题解题过程

数和形作为数学中两个作为古老与基本的研究对象，两者在一定条件下能够相互转化，高中数学主要研究的也是这两大部分，代数对应的是“数”，几何则与“形”相对应，应用题也是围绕着两个方面设置的.因此，为实现高考中数学应用题的瓶颈突破，教师应指导学生运用数形结合思想分析和处理应用题，促使他们通过以数解形或以形助数优化解题过程.

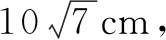
(1)将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；

(2)将放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求没入水中部分的长度.

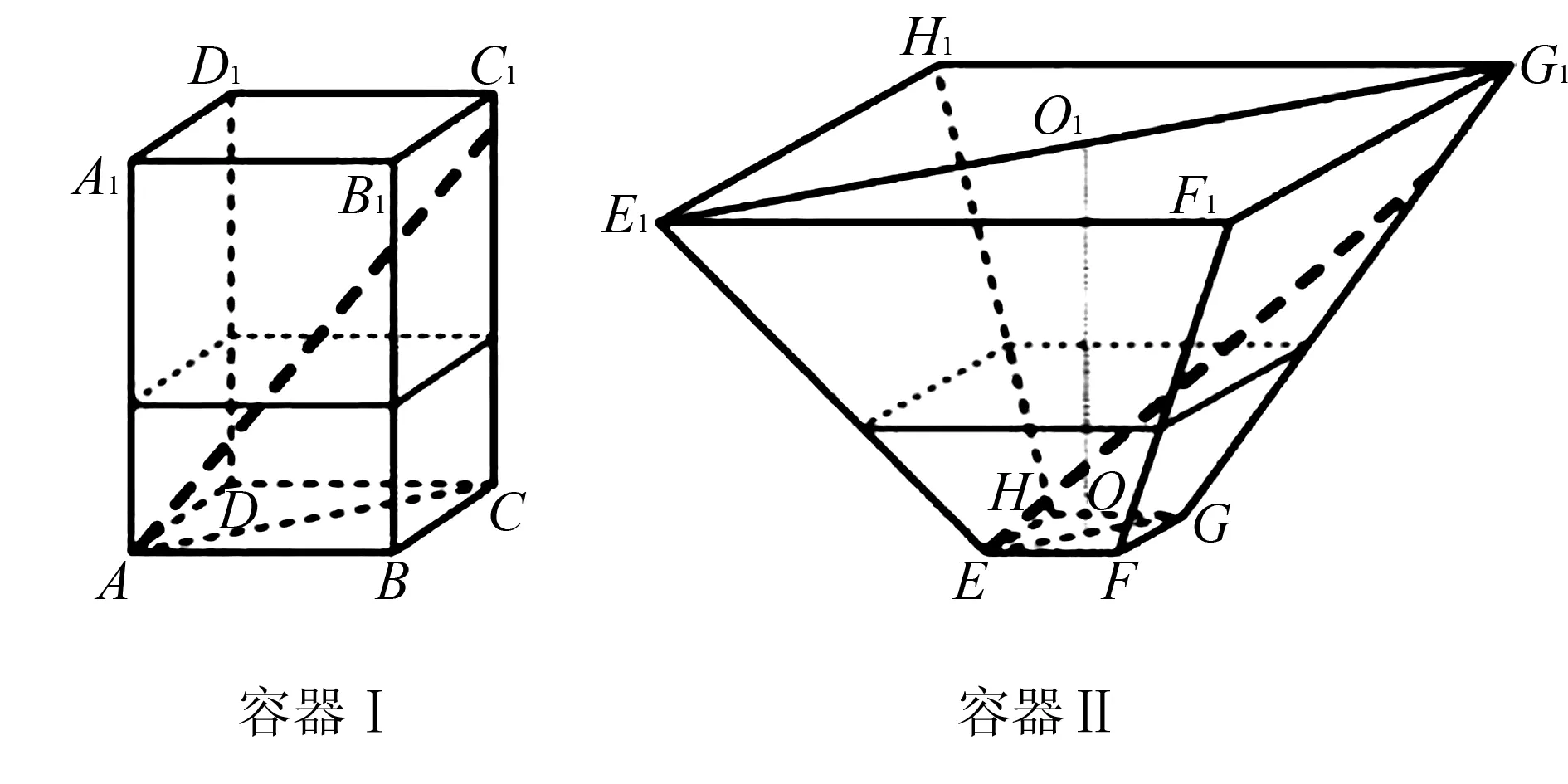
图3

本题考查玻璃棒l没入水中部分长度的求法，学生可用数形结合思想、化归与转化思想分析题目，结合空间中线线、线面、面面间的位置关系等基础知识来解题，优化他们的解题过程，使其推理论证、运算求解、空间想象能力得以锻炼.

四、积极建立数学模型，把握解决应用题关键

数学建模就是根据实际问题来建立数学模型，对数学模型来进行求解，再根据结果去解决实际问题，而应用题大部分都是实际问题，这为数学模型思想的应用提供良好契机.从本质上来讲，在高中数学中，应用题同实际生活联系的最为密切，解题的关键在于数学模型的建立，教师需意识到这一点，指引学生积极建立数学模型，使其把握应用题的解题关键.

例4某农场有一块农田，如图所示，它的边界由圆O的一段圆弧(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米，点P到MN的距离为50米.现规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形ABCD，大棚Ⅱ内的地块形状为△CDP，要求A，B均在线段MN上，C，D均在圆弧上，设OC与MN所成的角为θ.

(1)用θ分别表示矩形ABCD和△CDP的面积，并确定sinθ的取值范围；

(2)若大棚Ⅰ内种植甲种蔬菜，大棚Ⅱ内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4∶3，求当为何值时，能使甲、乙两种蔬菜的年总产值最大.

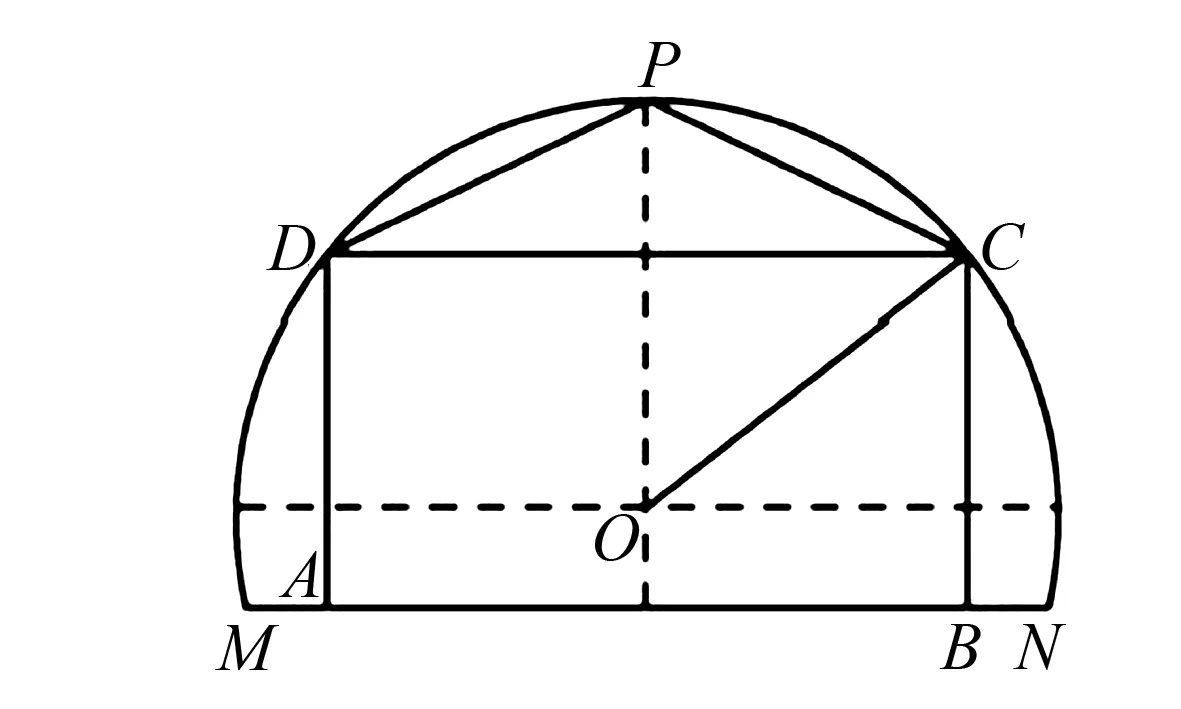
图4

本题主要考查三角函数的应用、用导数求最值等基础知识，以及直观想象和数学建模能力，教师要指引学生建立数学模型，使其运用所学知识分析与解决这一实际问题.

总而言之，在数学应用题具有相当高的实践考察价值，可以检测学生对知识点的掌握与运用情况，其实高考数学应用题并非像想象中那样不可逾越，教师需指导他们认真审题、正确运用解题方法，最终在高考中获得理想的成绩.