借助物理模型解答物理习题

罗金茂

(福建省上杭县第二中学 364200)

物理模型是对一些情境中物理规律的抽象与总结，不仅有助于学生更好的理解物理知识本质，而且可给学生解题带来良好启发，使其迅速的找到解题突破口，实现高效、正确解题.课堂上为使学生认识到物理模型的重要性，锻炼其运用物理模型解题的意识与能力，应优选精讲相关的物理习题，使学生积累丰富的模型应用经验.

一、杆绳速度分解模型

教学实践发现，部分学生解答杆绳速度分解问题时往往找不到正确的角度，导致速度分解出错.事实上，遇到该类问题可运用杆绳速度分解模型迅速作出判断.杆绳速度分解模型中与杆、绳连接物体的运动速度是合速度，沿杆、绳以及垂直杆、绳的速度均为分速度.在解题过程中牢牢把握这一关系，运用几何以及速度分解法则，能很快的得出正确结果.课堂上为使学生更好的体会该模型在解题中的应用，可与学生一起分析如下习题，帮助其更好的理解与掌握杆绳速度分解模型.

如图1所示，一段绳子的两端分别连接小车P和物块Q，跨过距地面高为H的两个定滑轮.起初小车处在左侧滑轮正下方的A点，而后以速度v匀速向左运动至B点，A、B的距离为H，则( ).

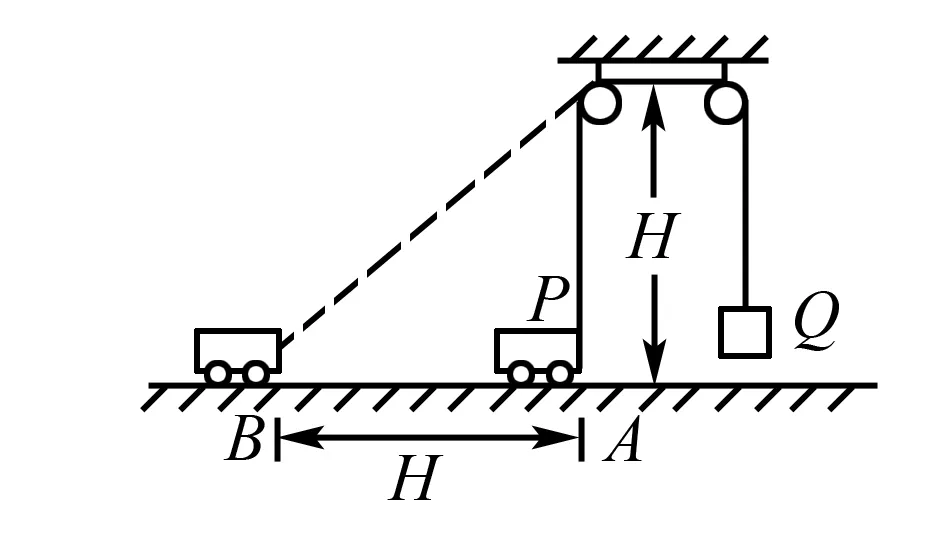
图1

A.物块Q匀速上升

B.Q上升时处于超重状态

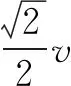
二、卫星运行与变轨模型

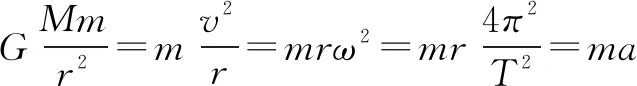
如图2所示，地球球心为O，一宇宙飞船沿椭圆轨道围绕地球无动力飞行，P为轨道上距离地球的最远点，PO=3R，已知地球半径为R，表面重力加速度为g，忽略地球自转以及空气阻力，则( ).

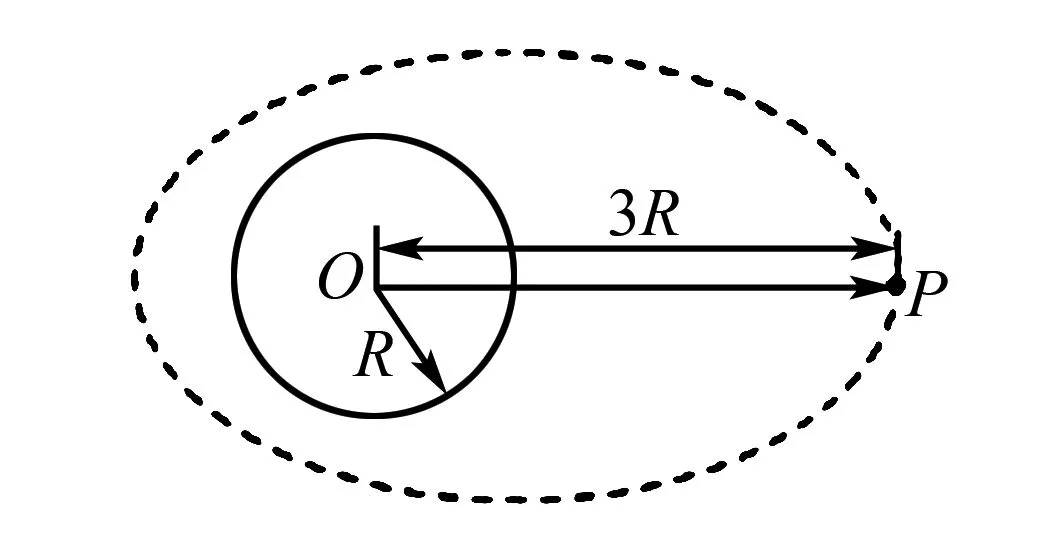
图2

A.飞船在P点的加速度一定是g/9

D.在P点时飞船变轨至为半径3R的圆形轨道，则需要制动减速

三、弹簧模型

弹簧较为特殊，其既能产生拉力，也能产生弹力.很多学生分析弹簧相关的物理习题时应对弹簧的受力特点理解不深入，难以短时间内找到有效突破口.事实上解答相关物理习题时运用弹簧模型能够更好的把握问题的本质，避免一些不良因素的干扰，提高解题正确率.弹簧模型主要体现在力和能量两个方面，其中力方面需要结合胡克定律、受力分析以及牛顿定律知识.分析的过程中应注重灵活运用整体与隔离思想根据需要转换分析问题的角度.在能量方面，弹簧的弹性势能属于机械能，其具有储能与释放能量的功能，解题时应注重灵活运用机械能守恒定律进行判断.

使用轻绳将三个质量均为1kg的木块a、b、c以及两个劲度系数均为500N/m的轻弹簧p、q连接在一起，通过定滑轮按照如图3所示放置，其中a所在的桌面光滑.开始时p处于原长，木块均处于静止状态，而后使用水平力F缓慢的向左拉弹簧p，当木块c刚好离开地面时，p弹簧的左端向左移动的距离为( ).

图3

A.4cm B.6cm C.8cm D.10cm

解析因整个过程缓慢进行表明物体均处于平衡状态.以弹簧q为研究对象，起初因b的重力弹簧会被压缩，由胡克定律可得kx1=mg，当c刚好离开地面时弹簧q被拉伸，由胡克定律可得kx2=mg，即，整个过程中弹簧q的长度变化为l=x1+x2；以弹簧p为研究对象，木块c刚好离开地面时，弹簧p的拉力刚好和b、c的重力之和相等，设弹簧p的伸长量为x3，则kx3=2mg；p弹簧的左端向左移动的距离为s=l+x3，代入数据解得s=8cm，选择C项.

四、物体碰撞模型

谈到物体的碰撞就需要运用动量守恒定律分析物体碰撞前后的速度变化.但是一些情境较为复杂，需要学生牢固掌握动量守恒定律的适用条件，把握构建物理方程的相关细节，即，应注重先设出物体运动的正方向.涉及到能量变化问题时，还需要运用机械能守恒定律.另外，考虑到相关的计算公式、计算过程较为复杂，应注重推导不同碰撞情境下的速度、能量变化规律，尽量牢记相关的推导结果，解题时直接的套用，能够大大提高解题效率.

如图4所示，A、B两个弹性小球静止在地面上方，B球距离地面的高度h=0.8m，A球在B球的正上方.先将B球释放，经过一段时间后释放A球.A球下落t=0.3s时，和B球在地面上方的P点相碰，碰撞时间极短，碰撞的瞬间A球的速度刚好为零.若B球的质量为A球的3倍.忽略空气阻力及碰撞的动能损失.求：(1)B球第一次达到地面的速度；(2)P点距离地面的高度.

图4

高中物理教学中应充分认识到模型的重要性，在日常的教学中通过运用多媒体课件，与学生一起分析、推导、总结常见的物理模型，进一步加深学生印象，使其把握物理模型的推导过程以及相关结论的来龙去脉，尤其应注重为学生讲解经典例题、组织学生开展针对性的训练活动，使学生在听课、训练中不断的深化对相关模型的理解，把握运用模型解题的细节，确保其在认识问题时更加深刻，考虑问题时更加全面，实现物理综合解题能力的明显提升.