线性规划 突破瓶颈
2021-08-19单文勇
单文勇
(江苏省如皋市第二中学 226500)
一、线性规划突破实根分布问题
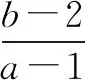
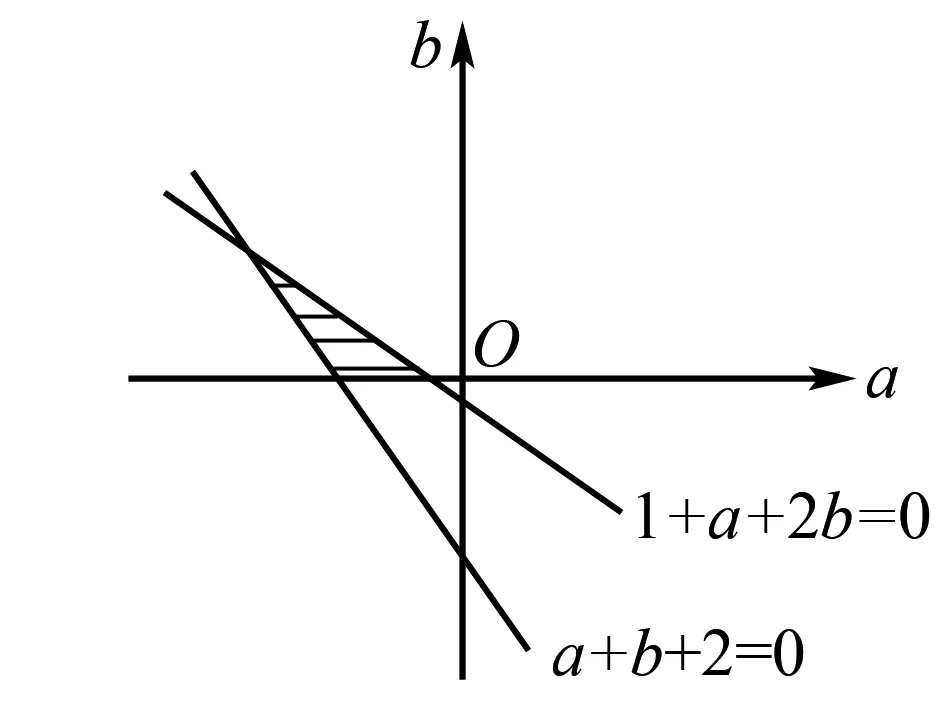
图1
解析设f(x)=x2+ax+2b,由二次方程根的分布,可得:
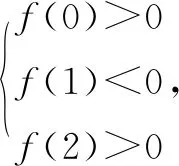
二、线性规划突破数列问题
例2设等差数列{an}的前n项和为Sn,S4≥10,S5≤15,则a4的最大值是____.
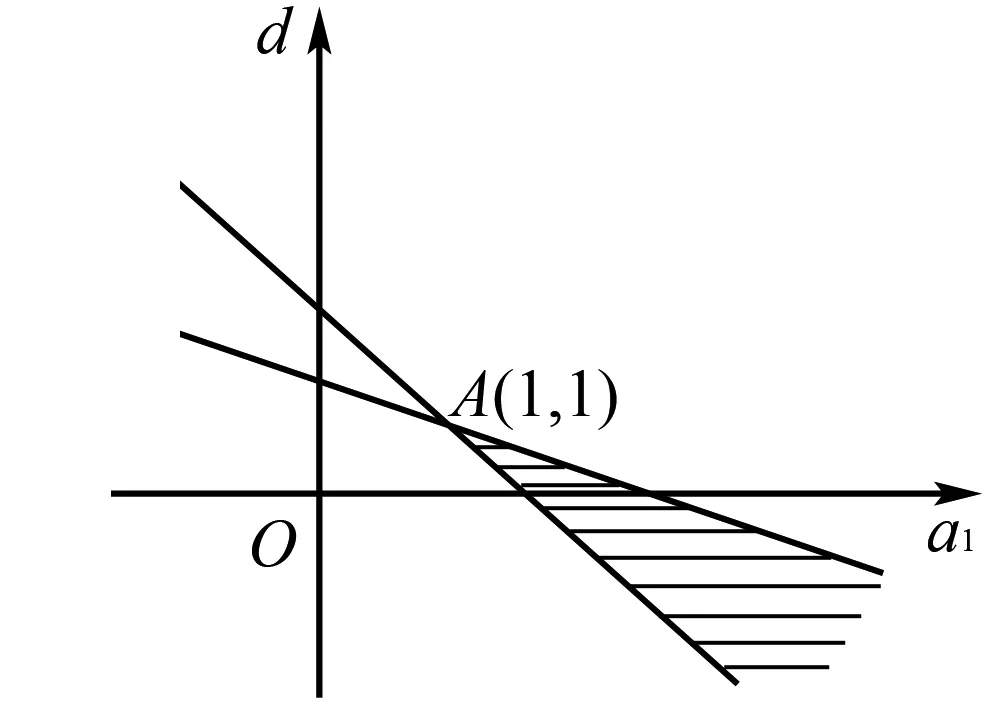
图2
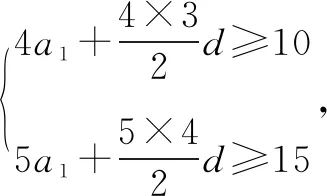
作出可行域:如图, 利用线性规划知识解决,应填4.
三、线性规划突破无理函数值域问题

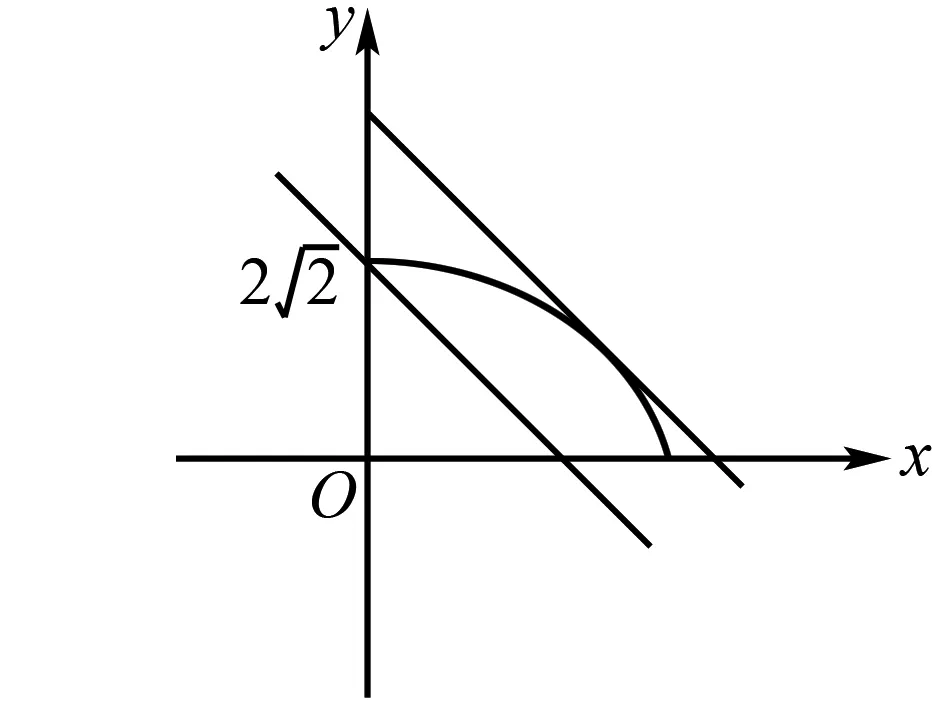
图3
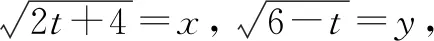
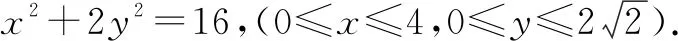
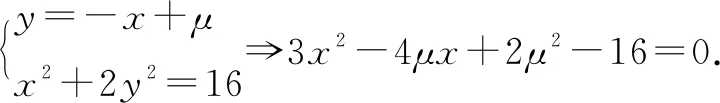
四、线性规划突破椭圆中最值问题

图4
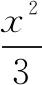
具体试验步骤为:①将加工好的煤样干燥后依次用三轴瓦斯渗流试验系统测定煤样的气体渗透率,每个煤样测定3次,取平均值作为该煤样液氮处理前的渗透率;②将煤样进行不同含水饱和度的制备,制备过程如第1.2节所述;③将制备好的不同含水饱和度的煤样放入保温容器中,向保温容器内注入液氮进行液氮冷浸试验;④冷处理结束后,待煤样恢复到室温后测量其冷处理后的渗透率。
五、线性规划突破概率问题
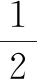
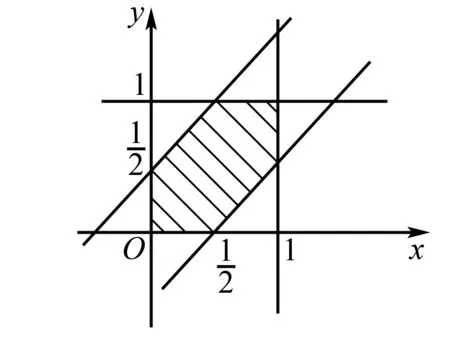
图5
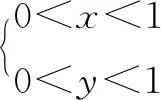
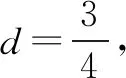
六、线性规划突破解三角形问题
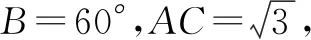

图6
解析由余弦定理可得3=a2+c2-ac,如果从曲线方程的观点去理解此式.
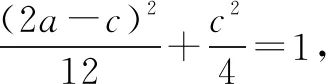
七、线性规划突破实际生活问题
例7本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
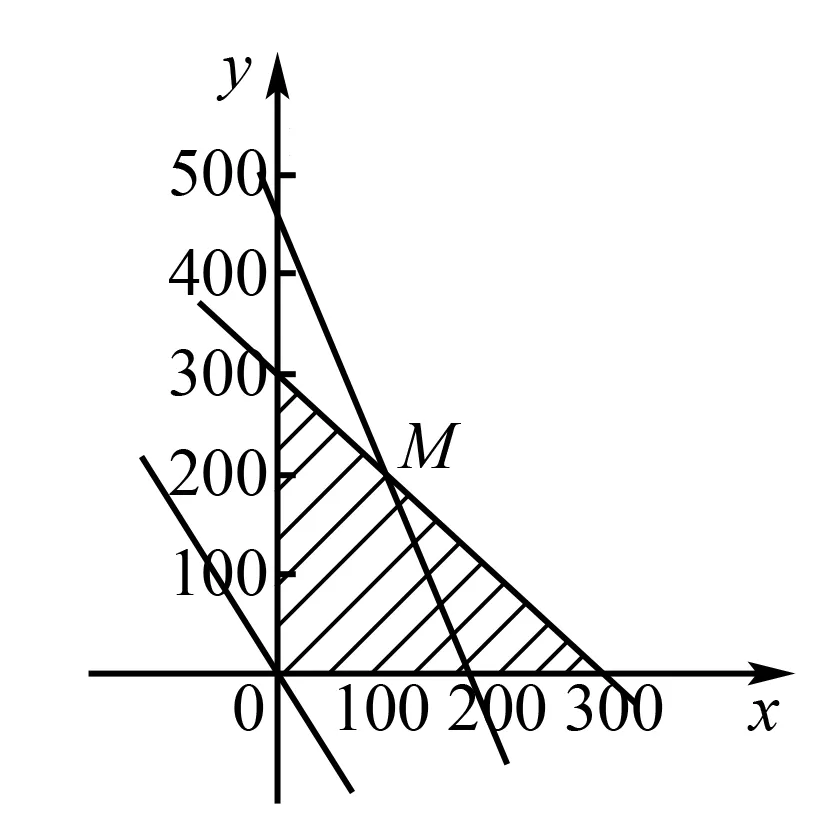
图7
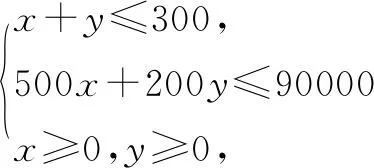
目标函数为z=3000x+2000y.
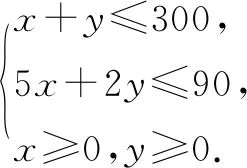
作出可行域:如图,利用线性规划知识解决可得
∴zmax=3000x+2000y=700000(元)
八、线性规划突破绝对值问题
例8已知实数x,y满足x2+y2≤1,则|2x+y-4|+|6-x-3y|的取值范围____.
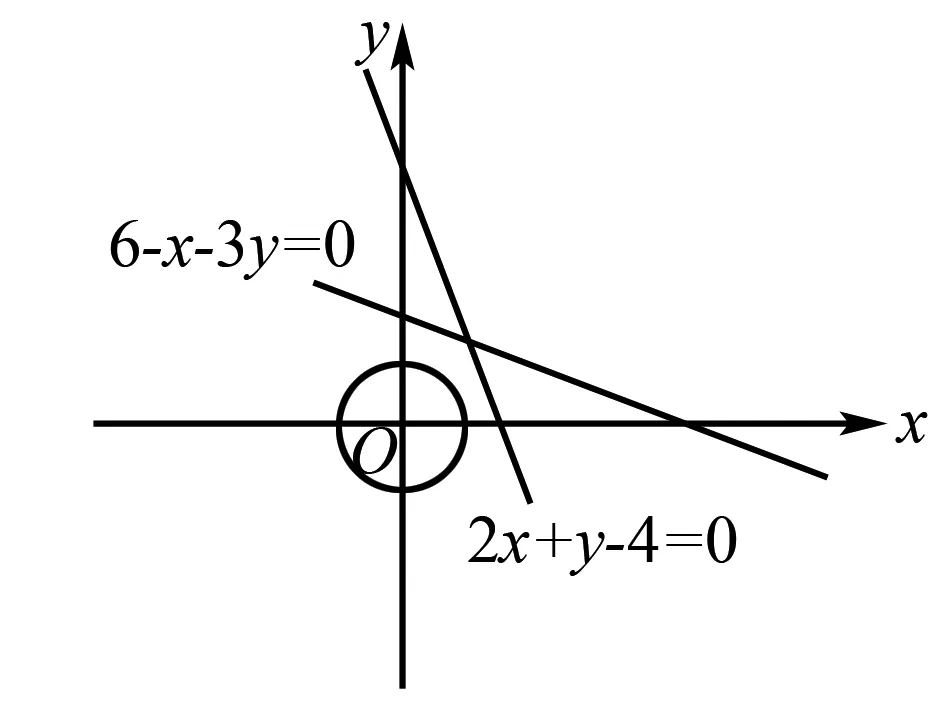
图8
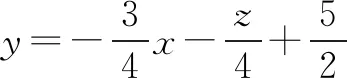
九、线性规划突破向量问题
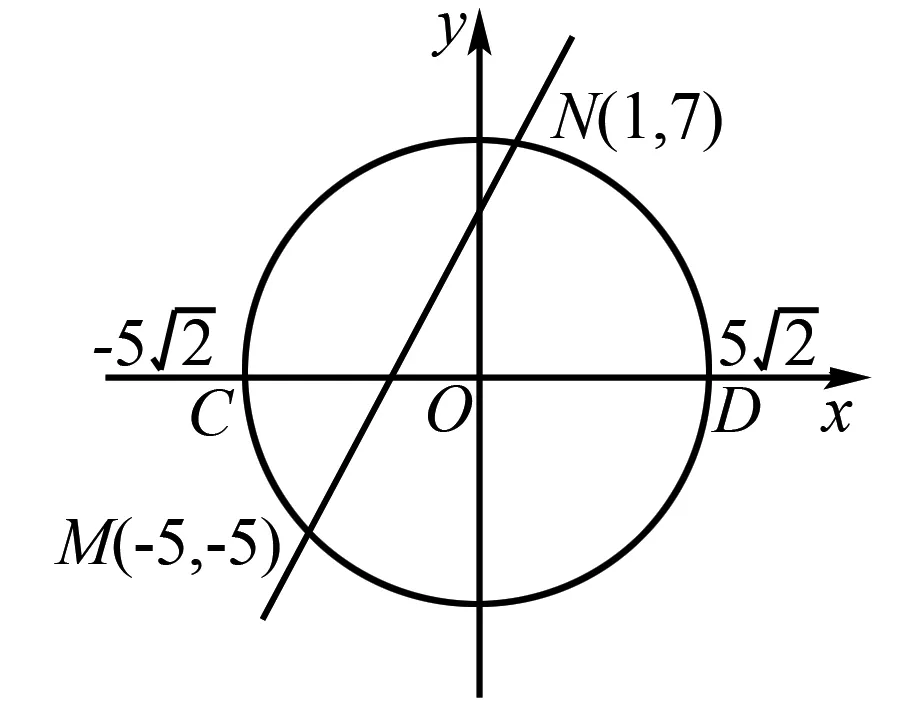
图9
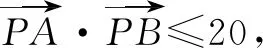
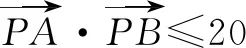
十、线性规划突破点线距问题
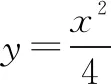
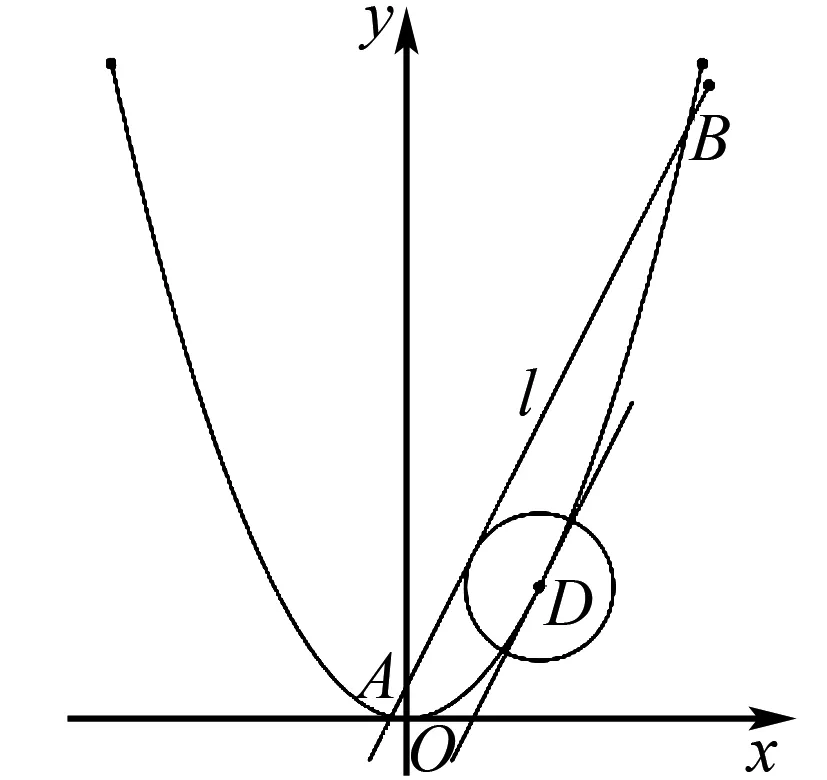
图10
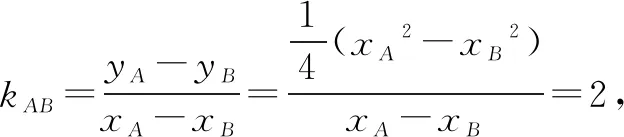

在数学学习中,掌握一定的数学思想方法远比掌握一般的数学知识要有用的多,数学思想方法是学习数学的“工具”,为我们解决数学问题提供清晰的思路.以上这些都是与“线性规划”似乎无缘的问题,但是都渗透了线性规划思想,利用线性规划思想去理解高中数学中一些问题,实际上是对数学形结合思想的提升,利用线性或非线性函数的几何意义,通过作图解决最值问题.是从一个新的角度对求最值问题的理解,对于学生最优化思想的形成是非常有益的.不仅开拓了学生的视野,而且锻炼了解题能力.
