多角度分析“双变量函数”问题的求解策略

邹景斌 朱贤良

(1.安徽省铜陵市第三中学 244000；2.安徽省枞阳县宏实中学 246700)

近些年来，“双变量函数”问题在高考或模考中备受青睐，屡见不鲜，成为高考与模考命题的常见角度，因而成为学优生力求攻克的难点.此类问题涉及的知识面较广、综合性较强、解法灵活，其求解过程中渗透着函数与方程、转化与化归、分类讨论以及数形结合等数学思想，因此此类问题能较好地评价学生的思维能力与应变能力.面对这类问题，很多学生常常是束手无策、缴械投降，或者无法正确转化、漏洞百出.

前段时间，笔者认真分析研究了高考与模考中的双变量试题，对此类问题的处理策略进行了归纳与整理，并在所带班级上了一节双变量函数问题的高三复习课，反响很好，并在课后检测中也得到了极好的反馈.本文以一道典型的模考试题为例，对双变量函数问题的求解思路作一全面分析，并整理如下，供读者朋友研讨与交流.

题目(2021届江淮创新联盟高三第二次联考·理22)已知函数f(x)=2bx-xea-x的图象在(-1,f(-1))处的切线方程为y=2(e-1)x-1.

(1)求函数f(x)的解析式；

(2)设关于x的方程ex-mx=0的两根为x1，x2,证明：x1+x2>2.

本文主要是从第二问分析此类双变量函数的解决策略，故第一问不做解释.

一、一题四法：从不同视角不同的处理方法攻克“双变量函数”问题

题中证明x1+x2>2是十分常见的试题类型，学优生对此应该不会陌生，比如2016年高考全国课标卷理科第21题即为同类问题：

已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围；

(2)设x1,x2是f(x)的两个零点，证明：:x1+x2<2.

此高考试题可供读者朋友研究，我们先从不同角度对上述联考试题进行分析.

1.灵活整理代换，变量巧妙归一

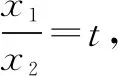
在本题中，由ex1-mx1=0和ex2-mx2=0可以得到

mx1=ex1

①

mx2=ex2

②

两式相加，可得m(x1+x2)=ex1+ex2

③

两式相减，可得m(x1-x2)=ex1-ex2

④

要证明x1+x2>2，只需证明

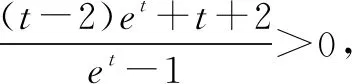
点评上述求解过程求解的关键一步在于巧妙减元，令x1-x2=t之后，思路清晰易理解，因而如何巧妙地将变量归一才是上述思路的精髓所在.

2.直接换元代换，消减变量归一

由题意，可得mx1=ex1

④

mx2=ex2

⑤

⑥

3.构造无参函数，化为函数单调

此方法也是一种非常常见的招数，先设法将两个变量x1,x2统一成x1或x2，再构造函数，借助函数的单调性实现证明.

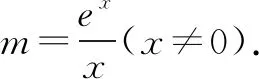
x(-㤲,0)(0,1)1(1,+㤲)g'(x)--0+g(x)↘↘e↗

要证明x1+x2>2，只需要证明g(x2)>g(2-x1)，而g(x1)=g(x2)，故只需证明g(x1)-g(2-x1)>0.

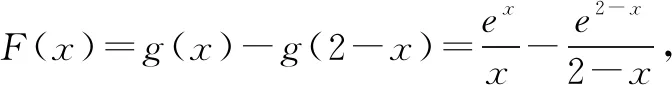
综上所述，g(x1)-g(2-x1)>0，即x1+x2>2.

点评以上解法是通过等价转化变形，使需要解决的问题等价化归转化为函数单调性的问题，从而实现求解.参考上述思路，也可以对称构造函数F(x)=g(1+x)-g(1-x)来进行求解，方法类似，在此不加赘述.

4.借平均不等式，快速化繁为简

在思路三中已经详细分析了x1,x2∈(0,+∞)且m>0，在下面解法中不再重复详细说明.

点评要证明x1+x2>2，就是证明式子中暗藏的不等关系，而通过重要不等式、基本不等式、对数平均不等式、柯西不等式等都可以体现式子中深层次的不等关系.解题时要善于观察，灵活多变地借用经典不等式来快速解题，做到大道至简，直击问题本质.

二、解题启示：刷百题不如透解一题

在解题教学中，笔者坚持“刷百题不如透解一题”这一信念.无论是在日常的备课还是课堂教学中，笔者都不自觉地思考是否还有其它的方法与思路来求解试题.对于经典试题，教师非常有必要引导学生从不同的角度进行思考，寻求多种多样的解法，让学生不盲从参考答案的方法，这样可以让各种思想在碰触中产生火花，激发学生的求知欲望，加速培养学生的发散思维，从而培养学生良好的思维品质，发展创造性思维.

总之，在平时的教与学中，如果我们能抓住看似普通的典型题目，站在数学思想和方法的高度，以培养思维能力和创新能力为目标，多角度、多方位分析和优化解法，必能以一题破万题，从而有效地减轻学习负担，提高学习效率.