分类讨论思想在数学解题中的运用
2021-08-19陈艳阳
陈艳阳
(江苏省南通市北城中学 226000)
一、利用分类讨论思想解决函数方程问题
方程问题是学生初中阶段必须掌握的一个数学知识点,但是由于学生的认知水平不足,数学知识储备量有限,在学习较为抽象的数学函数问题时,总是感到难以下手.当出现这种情况时,教师需要耐心引导学生,指导学生正确运用分类讨论思想解决相应的方程问题,提高学生的数学解题效率.
例1现已知一个方程式子(a-3)x|a-1|+x2-3=0,a满足什么条件的情况下,上述式子为一元二次方程?
解析从题目给出的信息可以得出,当x的指数小于等于2,且是自然数即可满足要求,即|a-1|≤2.学生在解决上述问题时,容易犯的错是,认为只有当指数为1时,才能满足题目要求,导致答案不完整.而引入分类讨论思想方法能够有效避免学生的这一错误,教师指导学生将所有的可能列出来,避免答案遗漏现象.当|a-1|=2,时,a=3或者a=-1,将a代入一元二次方程,可得到式子x2-3=0,或者3x2+3=0.当|a-1|=1时,解得a=2或者a=0,得到一元二次方程式为x2-x-3=0,或者x2-3x-3=0.而当|a-1|=0时,解得a的值为1,此时的一元二次方程式子为x2-5=0.通过上述解析,不难发现将分类讨论思想方法运用到数学解题中,有效避免答案遗漏的现象,学生的解题准确率有所提升.
二、利用分类讨论思想解决三角几何问题
三角形问题也是学生在解决数学问题中经常遇到题型,因为几何知识的抽象性和逻辑性,学生在解决这类问题时存在一定的难度.而且因为学生的空间想象力不足,难以准确理解此类问题的具体意思,解题思路自然存在偏差.因此,教师在教学时,需要有意识、有目的地培养学生的逻辑思维能力,锻炼学生的空间想象力.将分类讨论思想方法运用到几何问题解决中,有效帮助学生解决数学问题,提高学生的数学解题技能,确保学生的数学解题效率,增强学生的解题信心.
例2如图所示,已知两条直线l1和l2,以及一条线段AB,两条直线相交,假设两条线段上存在一点P,在什么情况下,能够满足△PAB为等腰三角形?
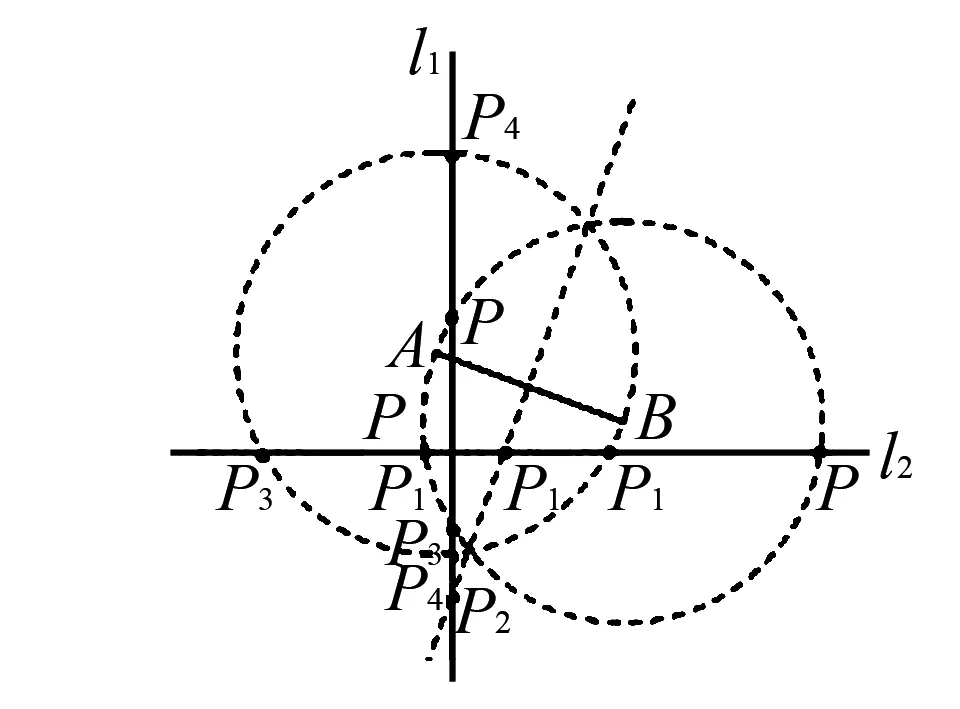
图1
解析学生在求解上述数几何问题时,因为缺乏较强的想象力,在解决问题上存在一定的难度,如果学生继续运用传统的解题方法,可能会导致答案错误.因此,教师需要指导学生正确解决上述问题,首先,教师需要帮助学生回忆有关等腰三角形的定义和相关知识,然后指导学生利用课堂所学知识进行求解,正确运用分类讨论思想方法,已知AB为等腰三角形的一条边,现在需要进行分类.首先,假设AB为等腰三角形的底边,在此条件下,作线段AB的中垂线,分别与直线l1和l2相交于点P2和P1,此时满足要求,即△PAB为等腰三角形.继续假设,当线段AB为等腰三角形的腰时,又需要进行分类.首先假设当∠A为顶角时,教师引导学生利用课堂中与等腰三角形的定义知识,指导学生作图.以点A为圆心,线段AB为半径画一个圆,和直线l1和l2相交于点P3、P4、P5和P6,即满足上述题目的要求.当∠B为顶角时,同理,以点B为圆心,线段AB为半径作圆,可得到和直线l1和l2的交点P7、P8、P9和P10,满足数学题目要求,△PAB为等腰三角形.由此可见,学生在解决初中数学三角问题时,应当正确指导学生利用分类讨论思想解决数学问题,提高学生的数学解题效率,确保初中数学课堂教学质量.
三、利用分类讨论思想解决圆的相关问题
几何数学知识是学生学习数学知识的重中之重,学生的逻辑思维不足,难以准确掌握数学几何知识.因此,教师需要正确引导学生.初中的几何知识包括三角形、圆形等几何图形,学生在解决这类问题时,因为对几何知识的理解不透彻,无法准确抓住题目的关键,从题意本身出发,导致答案错误.所以,教师需要指导学生动手作图,通过自主探索获得数学新知识,既锻炼学生的动手能力,又确保数学课堂的教学质量.
例3已知两个圆O1和O2的半径分别为10和17,两个圆存在两个交点A和B,线段AB的长为16,求圆心距O1O2和∠O1AO2?
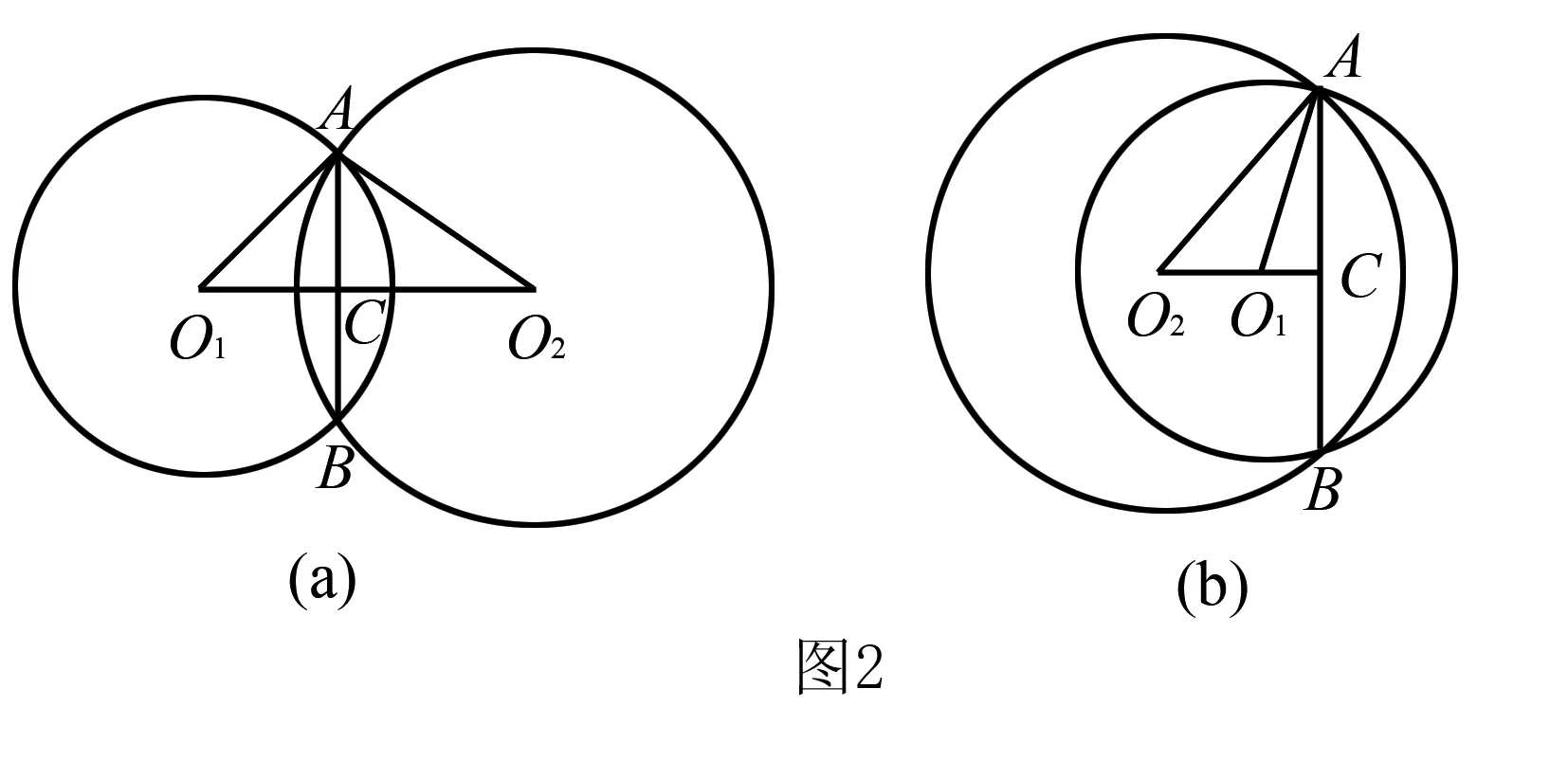
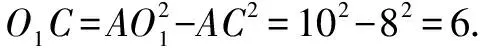
综上所述,分类讨论思想在初中数学解题中运用较为广泛,教师需要合理准确地引导学生利用分类讨论思想,仔细审题,根据题目所给的信息,具体分析数学题目,确保答案的准确性,提高学生的解题技能,发展学生的数学思维.
