Adaptive input-to-state stable synchronization for uncertain time-delay Lur’e systems

Zhi Zhang(章枝),Zhilian Yan(闫志莲)Jianping Zhou(周建平),3,4 and Yebin Chen(陈业斌)

1 School of Computer Science&Technology,Anhui University of Technology,Ma’anshan 243032,China

2 College of Electrical Engineering & Automation,Shandong University of Science and Technology,Qingdao 266590,China

3 Research Institute of Information Technology,Anhui University of Technology,Ma’anshan 243000,China

4 Anhui Province Key Laboratory of Special Heavy Load Robot,Anhui University of Technology,Ma’anshan 243032,China

Abstract This paper is dedicated to the study of adaptive input-to-state stable synchronization of uncertain time-delay Lur’e systems with exterior interference.With the help of the Lyapunov function approach,a sufficient condition for the input-to-state stability of the synchronization-error system is derived,which is theoretically less conservative than a previously reported criterion in the absence of parameter uncertainties.On the basis of the present condition,a co-design of the feedback gain and estimates of the uncertain parameters is given to determine the desired adaptive synchronization controller.Finally,an example with simulations is provided to demonstrate the applicability and superiority of the analysis and design strategies.

Keywords:input-to-state stability,Lur’e systems,parameter uncertainty,adaptive control

1.Introduction

Lur’e systems are a class of typical nonlinear dynamic systems that include a number of different chaotic models,such as Chua’s circuits,Hopfield neural networks,Lorenz systems,and genetic oscillators,as their special cases.Over the past few decades,synchronization of Lur’e systems without and with time-delay has attracted increasing attention from researchers in various disciplines owing to their applications in image encryption as well as secure communication[1,2].Corresponding,plenty of research results regarding the synchronization of Lur’e systems have been proposed in the literature;see,e.g.[3–7]and the references therein.

An actual dynamic system inevitably suffers from exterior interference of varying degrees,which may have a great influence on the synchronization behaviors.Considering that the existing interference is bounded in most cases,it is of necessity to make sure that the state of the synchronization-error system(SES)is also bounded.This issue,called the input-to-state stable(ISS)synchronization problem[8–11],has drawn the interest of researchers in the control community.Nevertheless,it seems that there are few results available on ISS synchronization of timedelay Lur’e systems despite their importance.

On the other hand,structure and parameter uncertainties often exist owing to modeling errors.It is often the case that one has very little information on the bound of these uncertainties,which had led in the past decades to a focus on the adaptive control scheme,with the belief that such a control scheme not only is easy to be implemented,but also can relatively smoothly and accurately track the system trajectory during normal operation[12].For time-delay Lur’e systems,although the adaptive control approach has been considered in[13–15],how to use it to achieve ISS synchronization of uncertain time-delay Lur’e systems with exterior interference is still unclear and deserves further detailed investigation.

In this paper,we attempt to study the issue of adaptive ISS synchronization for uncertain time-delay Lur’e systems with exterior interference.The main contributions of our work are twofold:A sufficient condition on the ISS of the SES is derived with the help of the Lyapunov function approach.It is theoretically less conservative than the criterion presented in[16]when there are no parameter uncertainties in the Lur’e system;

A co-design of the feedback gain and estimates of the uncertain parameters is given to determine the desired adaptive synchronization controller.It depends on the feasibility of few linear matrix inequalities(LMIs)and,therefore,is numerically tractable.

2.Preliminaries

Consider a type of Lur’e system modeled as

Remark 1.Lur’e system is a common type of nonlinear system formed by a linear time-invariant system and a feedback loop involving nonlinear dynamics.Such systems are capable of generating strange chaotic attractors and,thus,of great application potential in image encryption and secure communication.It is worthy to point out that the Lur’e system model considered herein includes many famous chaotic models,such as the Lorenz systems,Chua’s circuits,and chaotic Hopfield neural networks as its special cases.

In the past decades,chaotic synchronization has aroused great interest in various fields.The existing schemes of synchronization can be roughly divided into two types:the coupled synchronization[17–19]and drive-response(or master-slave)synchronization[20–22].In this paper,the drive-response scheme will be utilized.Let us set(1)as a drive(master)system and then set the following as the corresponding response(slave)system:

in whichζ2(t)∊Rm,u(t)∊Rm,andη2(t)∊Rnstand for the state,input,and output vectors,respectively;ε2∊Rn×lis a constant matrix.

Define∊(t)=ζ2(t)-ζ1(t).Then we are able to establish the following SES:

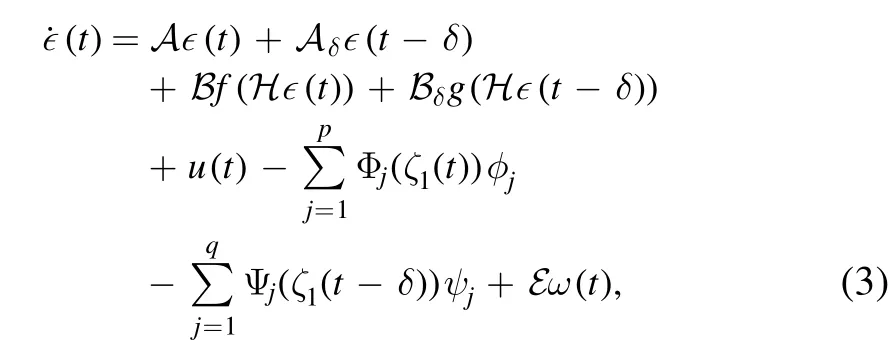
in which

In the paper,the adaptive control approach will be adopted.The form of the controller is as follows:

Remark 2.In order to achieve synchronization of Lur’e systems,a lot of control strategies including the PD control[6],the adaptive control[13–15],the sampled-state feedback control[23],the time-delayed feedback control[24],the output-feedback control[25],and the sliding mode control[26]etc,have been utilized.Among these control strategies,the adaptive control method not only is easy to be implemented,but also can relatively smoothly and accurately track the system trajectory during normal operation[12].When the drive system under consideration is subject to structure and parameter uncertainties,such a control method serves as an ideal candidate.

Substituting(4)into(3),one has

In what follows we give the definitions of ISS and ISS synchronization:

Definition 1.Suppose that there are aK function γ(ρ)and a strictly decreasing function β(t)that converges to 0 ast→∞.Then,system(5)is called to be ISS if

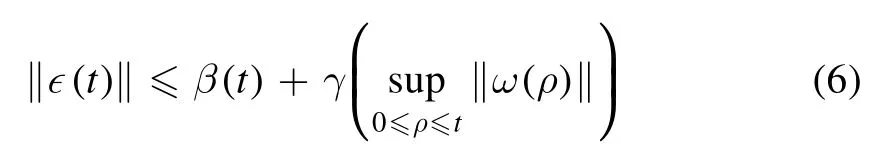
holds for each t≥0.

Definition 2.Systems(1)and(2)are said to be ISS synchronized if their SES(5)is ISS.

Remark 3.In a physical system,exterior interference is usually unavoidable,which is able to make the system oscillating,unstable or difficult to synchronize.Generally,the interference is not known a priori but is bounded in most cases.It can be observed from definition 1 that the ISS means that the system not only has bounded state under any bounded interference input but also is Lyapunov asymptotically stable in the absence of the interference.Thus the ISS may serve as a bridge among the input-output stability and the Lyapunov stability[27].Especially,ifβ(t)is chosen to beβe-εt[28],where β and ε are positive constants,then the ISS implies the exponential stability for the zero interference input case.Therefore,it is of great significance to study the ISS synchronization problem of Lur’e systems with exterior interference.

In this paper,the aim is to give a design of a adaptive controller in the form of(4)to make sure that the drive and response systems(1)and(2)to be ISS synchronized.

To accomplish the aim,let us introduce the following assumption,which is frequently applied in the literature[29–33]:

Assumption 1.FunctionsF1(·),…,Fm(·),G1(·),…,andGm(·)are global Lipschitz continuous;that is,there exist constantsLfi≥0andLgj≥0,i=1,…,m,j=1,…,msuch that

for any α,β∊R.

Besides,we prepare two necessary lemmas,where the proof of lemma 2 is not difficult and is omitted herein for brevity:

Lemma 1.[34]Given real matrices P and Q of suitable size,for any real constant θ>0 we have

Lemma 2.For anyω(ρ)∊C([a,b],Rn)(a,b∊R),the following equality holds true:

3.Main results

This section is focused on the ISS analysis and the corresponding adaptive synchronization controller design.The following criterion regarding the ISS analysis of the SES in(5)can be established:

Theorem 1.Suppose that there are scalars θ1>0,θ2>0,and matrices P,Q,R,S∊such that

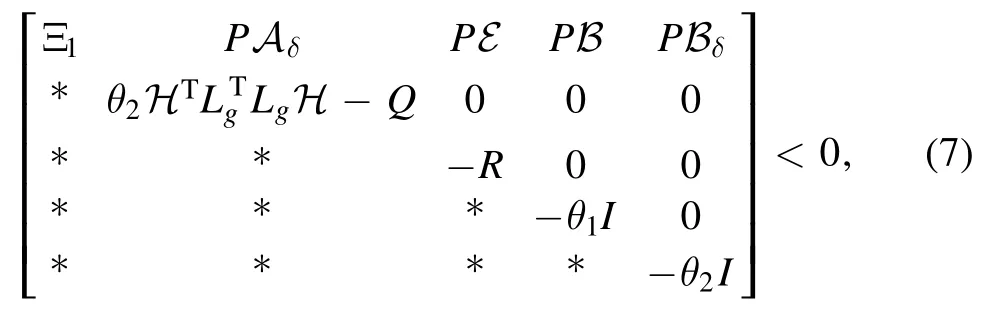
where

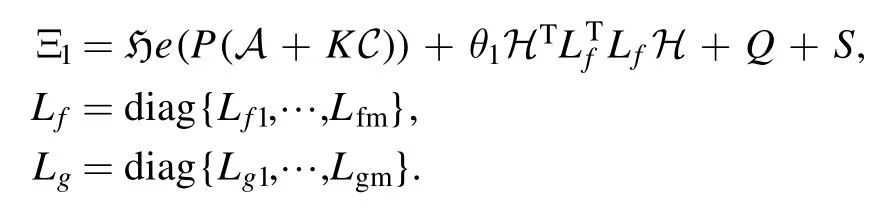
Then,system(5)is ISS if

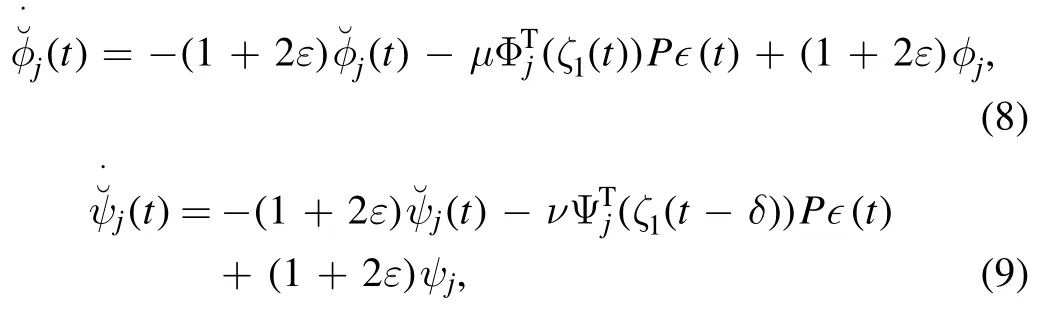
whereεis a scalar satisfying

andμ,ν are any positive scalars.

Proof.Let us select a Lyapunov function as

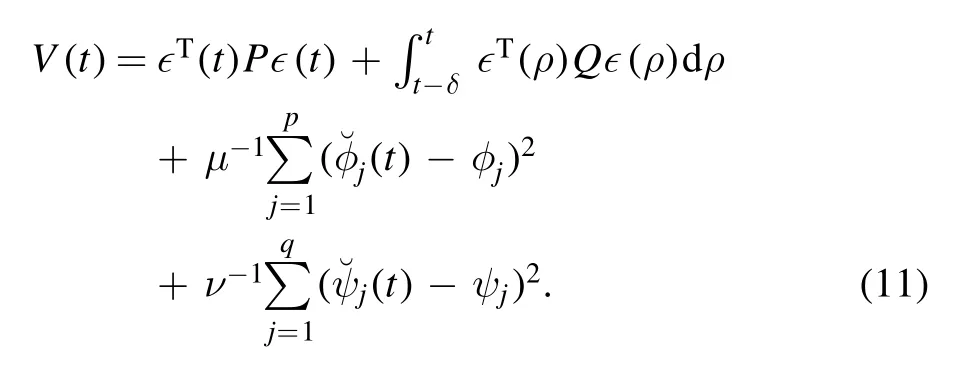
We have along system(5)that

With Assumption 1,the following inequalities hold true:

which together with lemma 1 result in

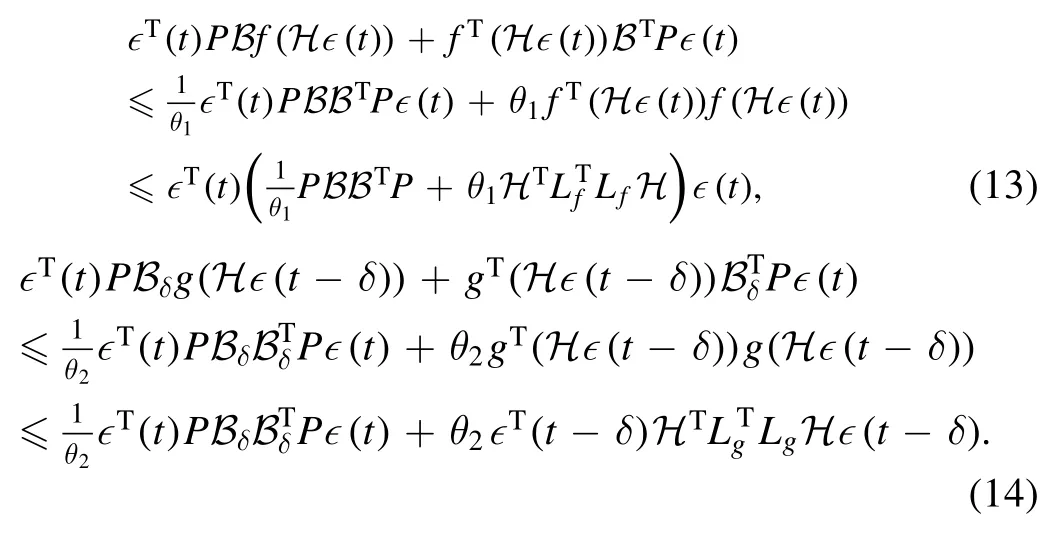
Noting(13)and(14),it follows from(12)that

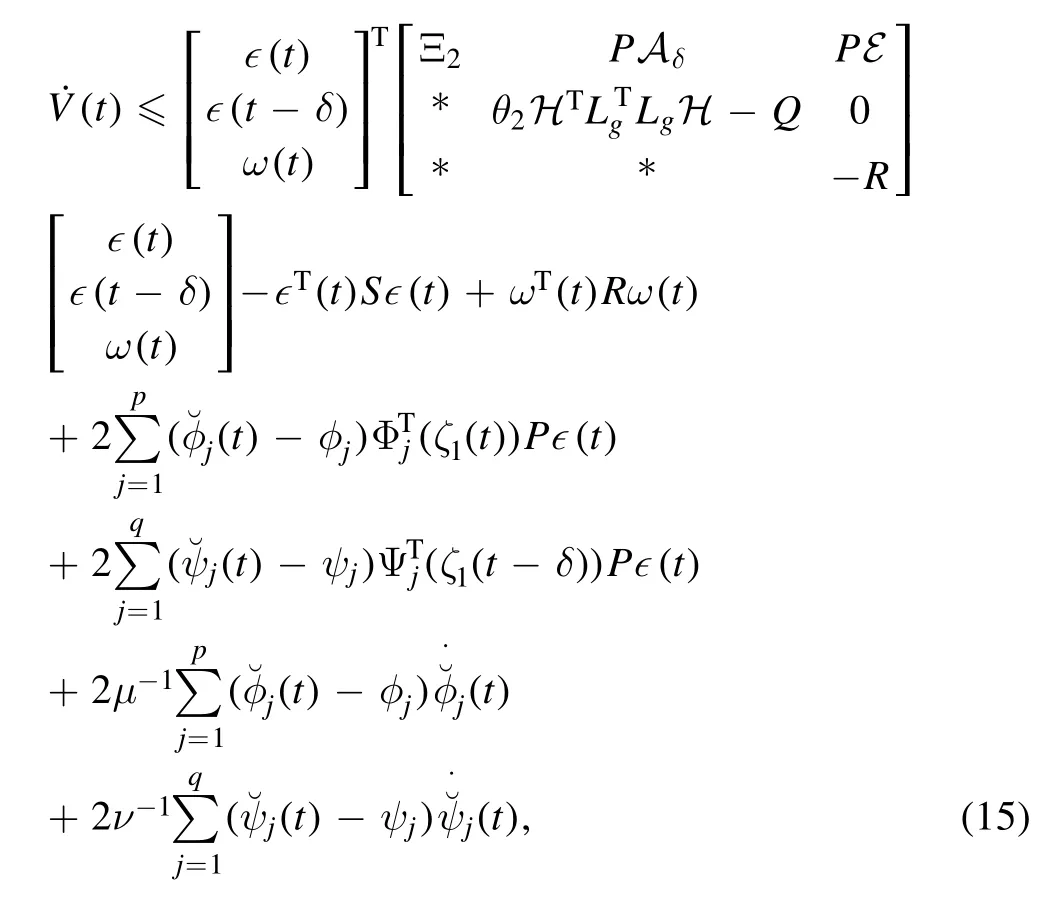
where

According to Schur’s complement,(7)ensures that

Using(8),(9),and(16),we have from(15)that

Deriving the derivative of e2εtV(t)and using(11)and(17),one gains

By integrating both sides of(18)from 0 to t,one has

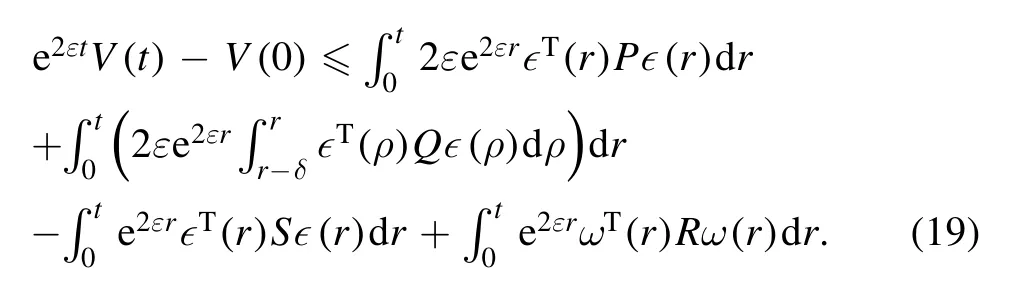
From the second term on the right hand side of(19),it can be calculated that

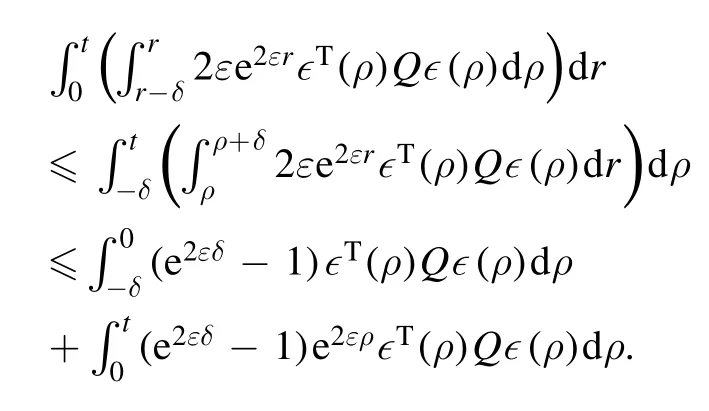
Substituting the above inequality into(19),we can obtain

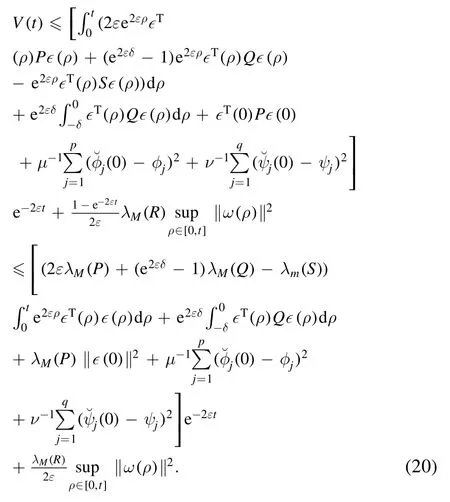
On the basis of(10),it follows by(20)that

On the other hand,it is effortless to get

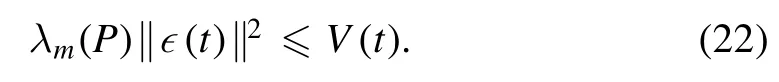
Now,using(21),(22)and lemma 2,we can get(6),where

with

Therefore,system(5)is ISS and the proof is finished.

Remark 4.When ω(t)≡0,it can be seen from the above proof that system(5)is exponentially stable with decay rate ε under the conditions of theorem 1.

Next,attention will be concentrated on the no parameter uncertainties case(i.e.φj≡ψj≡0).In this case,system(5)becomes

And one can write the following results:

Corollary 1.System(23)is ISS if there exist scalars θ1>0,θ2>0 and matrices P,Q,R,S∊such that

where

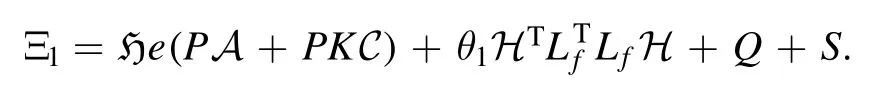
Proof.Let us select a Lyapunov function as

Then,along parallel lines as the proof of theorem 1,one can readily reveal that system(23)is ISS for any bounded interference ω(t).

In[16],the ISS filtering issue for delayed nonlinear systems was considered.With the application of a more complicated Lyapunov function as

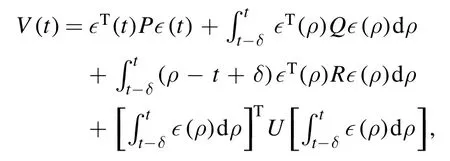
together with the analysis approach therein,the following criterion concerning ISS of system(23)was obtained:

Proposition 1.[16]System(23)is ISS if there exist matrices P,Q,R,S1,S2,U∊such that

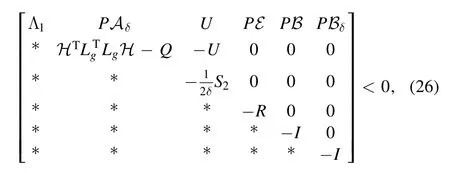
where

Remark 5.With the aid of Schur’s complement,it is not difficult to see that(24)is a necessary condition for establishing(26),which means that the present ISS analysis approach is less conservative than that proposed in[16].

Now we are in a position to present our design method for the adaptive synchronization controller in(4)via the following theorem.

Theorem 2.Suppose that there are scalars θ1>0,θ2>0,matrices P,Q,R,S∊and a matrixM∊Rn×msuch that

She was flushed and breathing hard when I entered her room. I slipped the tape into the recorder and held the microphone to her lips. Ruthie, Hannah, Molly?this is the most important tape. She held my hand and closed her eyes. Someday your daddy will bring home a new mommy. Please make her feel special. Show her how to take care of you. Ruthie, honey, help her get your Brownie uniform ready each Tuesday. Hannah, tell her you don t want meat sauce on your spaghetti（）. She won t know you like it separate. Molly, don t get mad if there s no apple juice. Drink something else. It s okay to be sad, sweeties. Jesus cried too. He knows about sadness and will help you to be happy again. Remember, I ll always love you.

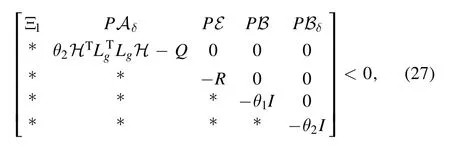
where

Then,under the adaptive controller in(4)with gain K=P−1M as well as updating laws(8)and(9),systems(1)and(2)are ISS synchronized.

Proof.With PK=M,the inequality of(7)can be rewritten as that of(27).Thus,systems(1)and(2)are ISS synchronized according to definition 2.

Remark 6.Once the LMIs in theorem 2 are feasible,one can obtain the feedback gain K as well as the estimates of the uncertain parametersφjand ψjsimultaneously.Note that there are efficient numerical algorithms available to check the feasibility of LMIs,such as alternating projection method,the ellipsoid method,and the interior-point method.Thus,the present design method of adaptive controller in(4)for ISS synchronization is numerically tractable.

4.Example

The section provides an example with simulations to show the applicability and superiority of the analysis and design approach.

Example 1.Consider the drive and response Lur’e systems in(1)and(2)subject to parameters

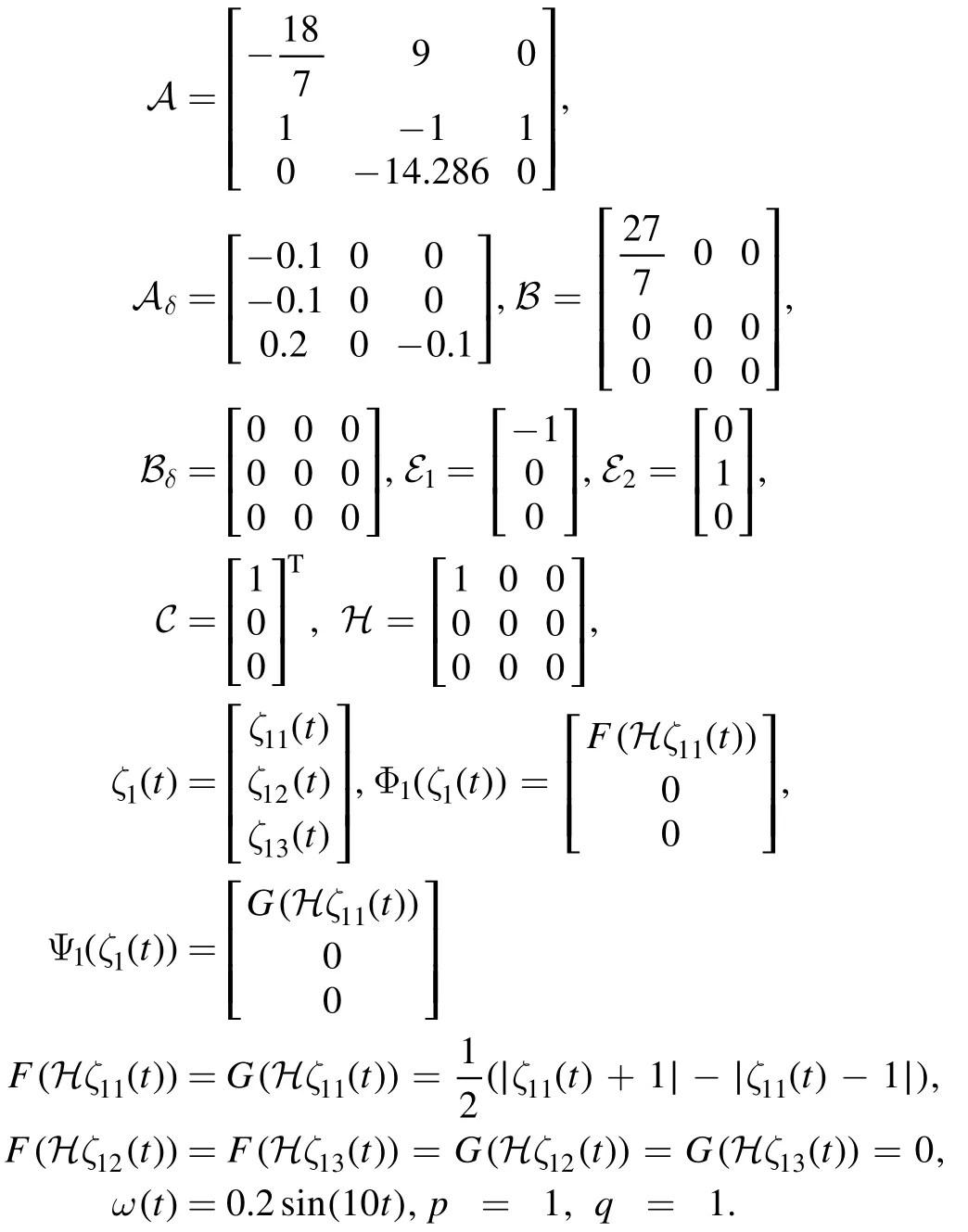
Notice Assumption 1 is satisfeid withLf=Lg=diag {1,0,0}.

When φj≡ψj≡0,(i.e.there are no parameter uncertainties),then the system considered in this example can be viewed as a time-delay Chua’s circuit[35].For this situation,both proposition 1 and corollary 1 can be used to check the ISS of the SES.However,as theoretically explained in remark 5,the former is much conservative than the latter.To illustrate this,let us consider the case thatK=k[1 1 1]T.Then,it can be verified that the LMIs in proposition 1 hold true for k≤-3.062,while,by corollary 1,it is observed that the ISS can be ensured even for k∊[-3.062,-1.651].

Next,let us show the applicability of our design approach.Solving the LMIs in theorem 2,we can obtain a feasible solution,where

Therefore,according to theorem 2,the ISS synchronization of the drive and response systems can be ensured under the controller in(4)with feedback gain

as well as updating laws in(8)and(9).

The simulations are carried out in MATLAB R2020b.As in[36],we consider the case when the uncertain parameters have different orders of magnitude.More specifically,the following two cases will be examined:Case A.φ1=0.02,ψ1=-0.005;Case B.φ1=-0.75,ψ1=-0.075.Under initial condition

figure 1 shows the chaotic behavior of drive system(1)for Case A.For Case B,the chaotic behavior is similar to figure 1 and therefore omitted herein for brevity.

Next,set μ=0.1,ν=0.1,ε=0.001,(0)=-0.5,=0.3,and randomly choose the initial value of response system(2)between-1 and 1 as follows:

Figures 2 and 3 show the state of the SES and the estimatesof φ1,ψ1with exterior interference for Case A and Case B,respectively;figures 4 and 5 further show the trajectories in the absence of exterior interference.It is found from these figures that the SES based on the designed adaptive controller is state-bounded under the bounded interference and quickly convergent in the absence of interference.Therefore,the simulations coincide with the present theoretical results.

Figure 1.Chaotic behavior.

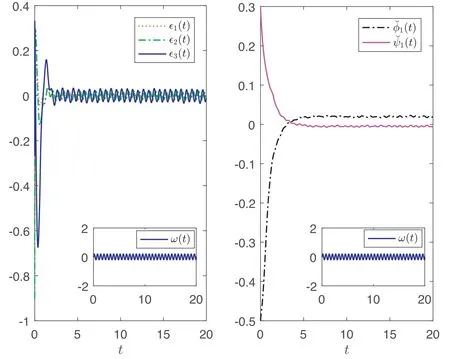
Figure 2.Trajectories of∊i(t)(i=1,2,3),andwhen(φ1,ψ1)=(0.02,-0.005).

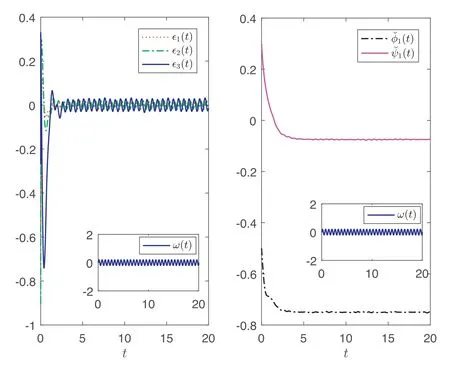
Figure 3.Trajectories of∊i(t)(i=1,2,3),andwhen(φ1,ψ1)=(-0.75,-0.075).

Figure 4.Trajectories of∊i(t)(i=1,2,3),,andwhen(φ1,ψ1)=(0.02,-0.005)and ω(t)≡0.

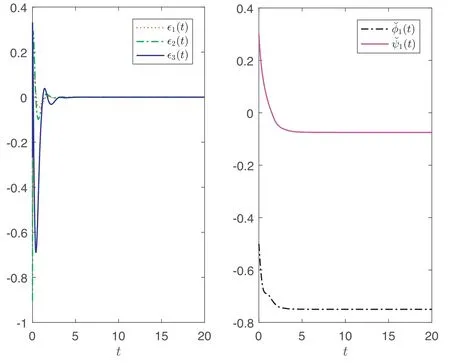
Figure 5.Trajectories of∊i(t)(i=1,2,3),andwhen(φ1,ψ1)=(-0.75,-0.075)and ω(t)≡0.

5.Conclusions

In this paper,the issue of adaptive ISS synchronization of timedelay Lur’e systems has been studied,where the exterior interference and parameter uncertainties have been considered simultaneously.With the aid of a Lyapunov function and some inequality techniques,a co-design of the feedback gain and estimates of the uncertain parameters has been proposed to determine the desired adaptive synchronization controller.For showing the applicability and superiority of the analysis and design approaches,an example with simulations has been given.

Acknowledgements

This work was supported by the Natural Science Foundation of the Anhui Higher Education Institutions(Grant No.KJ2020A0248),the National Natural Science Foundation of China(Grant Nos.61806004 and 61503002),and the Open Project of Anhui Province Key Laboratory of Special and Heavy Load Robot(Grant No.TZJQR005-2020).

ORCID iDs