基于GA-BP 算法的自适应均值滤波
2021-08-18窦艳艳孟巧云
窦艳艳,孟巧云
(南京高等职业技术学校,江苏南京,210019)
0 引言
椒盐噪声是图像在获取或传输的过程中生成的黑白点噪声,严重影响图像的质量。传统滤波方法有开关中值(SMF)滤波算法、极值中值(EM)滤波算法、递进开关中值(PSM)滤波算法、自适应中值滤波算法(AMF)等。BP 神经网络结构简单,实现起来比较容易,而且拥有较强的泛化性,适用于区分图像中的噪声像素和非噪声像素,但是BP 神经网络容易陷入局部极小,而且随机给出初始权值和阈值,以致训练时间较长,收敛速度慢。遗传算法在搜索时基于群体遗传和自然选择机理。遗传算法在求解问题时将问题的所有可能解都编码成个体,群体则是由若干个个体构成。遗传算法具有全局搜索的特性,开始时随机产生个体,将所有个体通过预定的目标函数进行评价得出适应度值,并基于适应度值进行优胜劣汰,将选出的“优”的个体通过交叉变异重新组合生成性能更优的新个体。
1 噪声检测模型
1.1 椒盐噪声模型
假设椒盐噪声灰度值在一定的范围内分布,例如8 位图像,则椒盐噪声灰度值的分布区间为[0,δ] ∪[255 -δ,255],其中δ代表0 或者较小的正整数,则图像中的像素f(i,j)可以分为信号点和噪声点两类,表示如下:
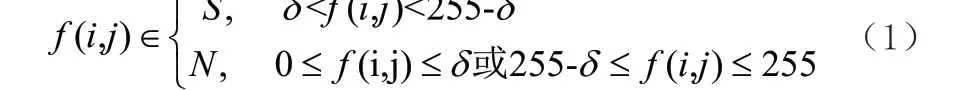
本文将δ取值为0,S 为信号点,代表非噪声像素集合,N 为噪声像素集合。
1.2 BP 神经网络结构
本文将棋盘格图像分成8 块分别加入不同级别密度的椒盐噪声,用原始图像与噪声图像进行相减,当两者之差不为0 时,标记噪声分布矩阵对应的位置值为1,反之该点值则记为0,从而得出图像噪声位置分布矩阵,并把它设置为训练网络时的目标图像。本文的 BP 神经网络的输入选用图像的像素值、中值和ROAD(Rank Ordered Absolute Difference)值,其中ROAD 值是Garnett 提出的区分信号点和噪声点时的一个重要因素。
其次为了使BP 网络结构简练同时也能较好地解决椒盐噪声检测,文中BP 神经网络的各参数设置如下:隐含层节点数目设置成“5”,最大训练迭代次数控制在200 以内,传递函数选择“tansig”和“purelin”,训练函数选取“trainlm”,网络训练允许误差设置成“0.02”。
1.3 遗传算法优化
BP 神经网络的初始权值和阈值是随机赋予的,通过遗传算法进行优化时,先用遗传算法对这些参数进行全局搜索,满足相应的条件后,再通过BP 神经网络在局部范围内实行最优搜索,直到设置的精度要求达到为止。BP 神经网络的一个权值或阈值就是遗传算法的一个个体,使用特定的方法对每个染色体进行编码,BP 算法的权值和阈值为最终得到的遗传算法的满意解。
(1)编码:将遗传算法优化过的神经网络的权值、阈值进行序列化成串,本文采用实数编码来解决由于编码的串太复杂太冗长而造成的遗传算法效率低下的问题。
(2)个体适应度评价函数:在遗传算法中当前群体的每个个体能够遗传到下一代群体中的概率大小取决于同个体适应度成正比例关系的概率,本文的适应度函数为实际输出和期望输出的误差平方和的倒数,即

其中A 表示实际输出,T 表示期望输出,n 是输入样本的个数。
(3)遗传算子:基本的遗传算子有选择算子、交叉算子和变异算子。将函数”normGeomSelect”作为本算法的选择算子,将”arithXover”作为本算法的交叉算子,将非均一变异函数”nonUnifMutation”作为本算法的变异算子。
1.4 决策规则
将神经网络的输出y 与阈值0.5 进行比较,其定义为
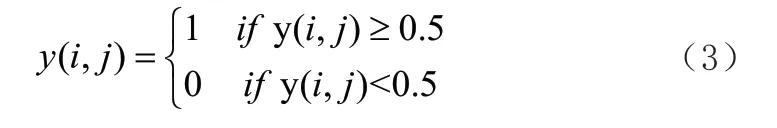
通过决策器后输出结果1 代表当前像素是噪声点,0 则表示当前像素为非噪声点,由此获取检测后的噪声分布图。
2 噪声滤除
椒盐噪声检测完得到精确的检测结果后,为了能够既有效的滤除图像中的椒盐噪声,又能很好的对图像的边缘等细节信息进行保护,本文的滤波算法仅仅只对噪声点进行处理,非噪声像素灰度值不变直接输出。针对图像中的噪声点,本文根据滤波窗口中没有受到椒盐噪声污染的像素的数量对窗口的尺寸进行自动调整。图像中像素与其邻域中像素的相关性大,所以本文将窗口中未被污染信号点的最小数目设为3 以使窗口尽量小,既保证了滤波质量又提高了滤波效率。具体滤波步骤如下:

(2)计算窗口中没有被噪声污染的像素的数量m,若15,转步骤(3),否则转步骤(4);
(3)如果m ≥2,则将窗口中所有没有被噪声污染的像素灰度值的均值作为输出;否则W=W+ 2,转步骤(2);
(4)如果W>15,窗口停止扩张,输出窗口中所有信号点的像素灰度值的均值;如果所有像素均被污染,则输出窗口内全部像素的均值。
3 滤波效果测试
为了避免偶然性造成测试误差确保获取的数据的可靠性,本文所得数据均为从12 组仿真结果中去掉最大值和最小值后剩余10 组数据取平均值。将峰值信噪比(PSNR)作为客观评价尺度,公式及相应参数如公式(4)所示:
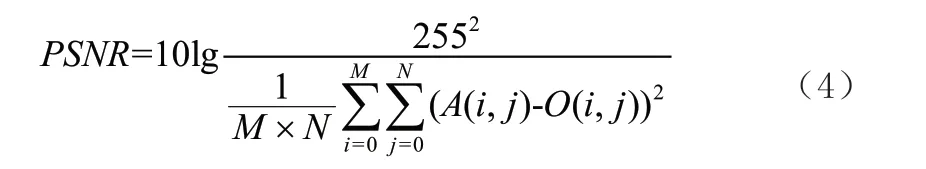
其中A 代表加入噪声后滤波后的图像,O 为原始图像,,像素点坐标为(i,j),图像尺寸为M×N。
为了测试本文提出算法的滤波性能,将图像大小均为512×512 的标准测试图像Lena、Boat、Baboon、Barbara、Peppers 分别采用四种传统滤波算法(SMF(3×3)、PSM、EM、AMF(17×17))以及本文提出的滤波算法,在不同强度噪声密度下,将图像中的椒盐噪声进行滤除,实验结果如表1 所示。
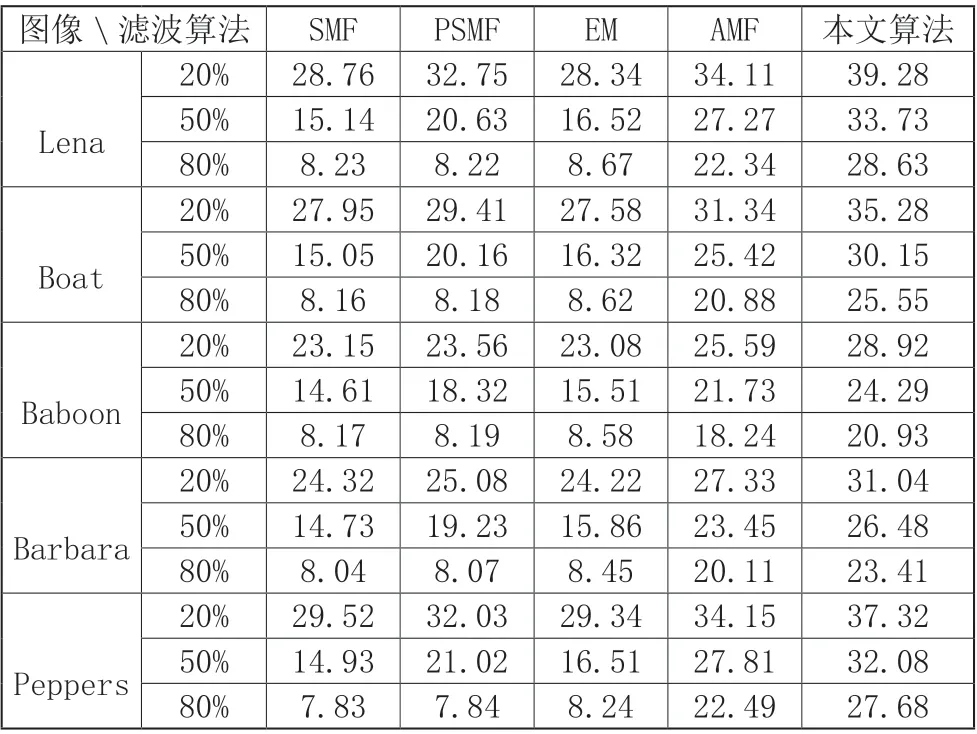
表1 各滤波方法PSNR 性能比较
由表1 中数据可见:本文提出的算法与传统滤波算法相比质量最好,尤其是当图像被噪声污染的密度愈大本文算法的优势愈明显。以测试图像中最为有名的Lena 图像作为标准测试图像对各种算法滤波性能进行详细地比较。图1 为各种算法对被10%至90%噪声密度的椒盐噪声污染后的Lena 图像进行滤波后的PSNR 值比较。
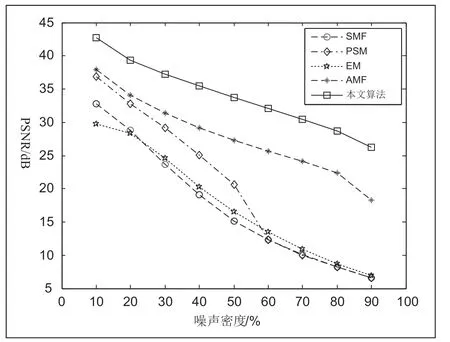
图1 各种滤波方法PSNR 值(Lena)
从图1 中清晰可见,SMF,EM 和PSMF 三种算法的噪声滤除能力比较接近,PSNR 值随着噪声密度的增大而降低。AMF算法的滤波性能相对比较稳定,但同一等级的噪声密度下PSNR 值平均比本文算法低6dB 左右,客观地说明了本文算法滤波性能的优越。随着噪声密度的不断增大,与传统滤波算法相比本文提出的算法优势更加明显。如图2 所示为90%噪声密度下各种算法滤波效果对比。

图2 各种算法在90%噪声密度下的滤波效果对比
由图2 可见,在高达90%噪声密度下SMF、PSMF 和EM三种方法效果极差,AMF 算法与前三者相较而言还是有质的飞跃的,但也不是完美的,其滤波后的图像如图2(e)所示,存在大量严重影响视觉效果的斑块。如图2(f)所示经本文算法滤波后的图像依然能够在去除噪声的同时保持较为细腻的细节。由此可见,本文算法不管是在客观PSNR 数据方面,还是在人的主观视觉效果方面都高于传统的滤波算法。
3 结束语
本文先用遗传算法将BP 神经网络的初始权值和阈值进行优化后再进行训练,用训练好的网络自动检测出图像中的椒盐噪声的位置,最后用本文设计的自适应均值滤波算法对噪声像素进行滤除,非噪声像素不进行任何处理直接输出。通过大量与其它几种传统的滤波算法的对比实验,验证了本文算法滤波性能的优越性,而且图像边缘等细节信息保存的比较完整细腻。
