百色市那坡水库溢洪道设计及其三维流场数值模拟研究
2021-08-18李熙
李 熙
(中科信德建设有限公司,四川 成都 610057)
那坡水库位于广西百色市南盘江之上,是兼有农业供水、防洪等功能的小(1)型水库工程。挡水建筑物为复合土工膜防渗风化料坝,坝轴线方位角N20.41°E,坝轴线长80.02m,坝顶高程1365.00m,防浪墙顶部高程为1366.00m,坝顶宽5.0m,下游坝坡在1347.00m高程设置宽度为2.0m马道,下游面采用格构加草皮护坡,顶宽5.0m。最大坝高35.5m(坝轴线处),坝底最大宽度82.6m。
在工程可研阶段需要对水库溢洪道进行设计,并结合实测模型与三维流场数值模拟,对数据合理性进行分析,通过模拟数据与设计成果对照,为设计参数的验证提供依据。
1 溢流坝段设计
重力坝具备挡水及宣泄水流的功能。溢流坝段溢洪道的设计,要保证溢流坝在挡水时满足抗滑稳定性及防渗要求,同时为充分满足溢洪道泄洪要求,要求对堰的型式及尺寸进行充分论证,下游衔接WES曲线的构造及设计要保证水流能够平顺地流向下游,尽量降低汽蚀和冲刷对水流消能的影响[1-2]。
1.1 定型设计水头的确定
Hzmax=校核洪水位-堰顶高程=1362.93
-1360.02=12.91m
不同设计水头堰顶最大负压见表1。

表1 不同设计水头堰顶出现的最大负压
本设计设计洪水位为50年一遇,取HS=Hzmax,即最大负压值为零,Hs=Hzmax=12.91m。
1.2 消能防冲计算
根据《混凝土重力坝设计规范》(DL 5108—1999),反弧半径为R=(4~10)hc,其中hc为闸门全开时,反弧段校核洪水最低点的水深,R介于24.88~62.2m之间,迭代法算出h1=hc=6.22m,反弧半径R=28m。鼻坎的高程为1339.5m,挑流鼻坎的挑角θ=24°。本设计选用校核洪水位工况作为计算工况。
(1)
式中q—校核洪水位时的单宽流量,q=118.7m3/s;
v——鼻坎处的平均流速,m/s;
φ——流速系数;
Z——上下游水位差,m;
h——坎顶水深,m;
b——溢流坝段净宽,本设计b=15m;
S——上游水位到鼻坎高程,S=452-429.5=22.5m。
挑流鼻坎挑射距离L按水舌边缘计算:
(2)
式中L——水舌挑距,m;
θ——挑射角度;
v1——坎顶水面流速,m/s。
经计算,L=33.182m。
最大冲坑水垫厚度计算公式为
tk=αq0.5H0.25
(3)
(4)
上二式中tk——自由面至坑底水垫的厚度,m;

α——冲坑系数,取1.2;
q——单宽流量,m3/s;
H——上下游水位差,m;
H2—下游水深,m。
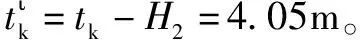
1.3 溢流坝面水面线计算
以下根据《水力计算手册》第6卷进行水面线计算[3]。
1.3.1 确定自然掺气开始发生点的位置
已知q=118.7m3/s,则
Lc由《水工设计手册》第六卷X与Hd比值确定,X的确定是在堰的顶部逐步向下游算得,切点(13,6.5)处Xt=13.0m,Hd=13m,X/Hd=1时,Lct/Hd=1.462,因此Lct=1.462×13=19.01m。
堰顶上游段的曲线长度,Lcu=0.315Hd=0.315×13=4.095m。
L=Lcu+Lct=19.01+4.095=23.105m。
Lk>Lcu,因此溢流堰上不会发生掺气。
1.3.2 坝头水面线计算
由于H=1362.93-1360.02=12.91m和Hd=11.24m,H/Hd=1.15,计算结果见表2。
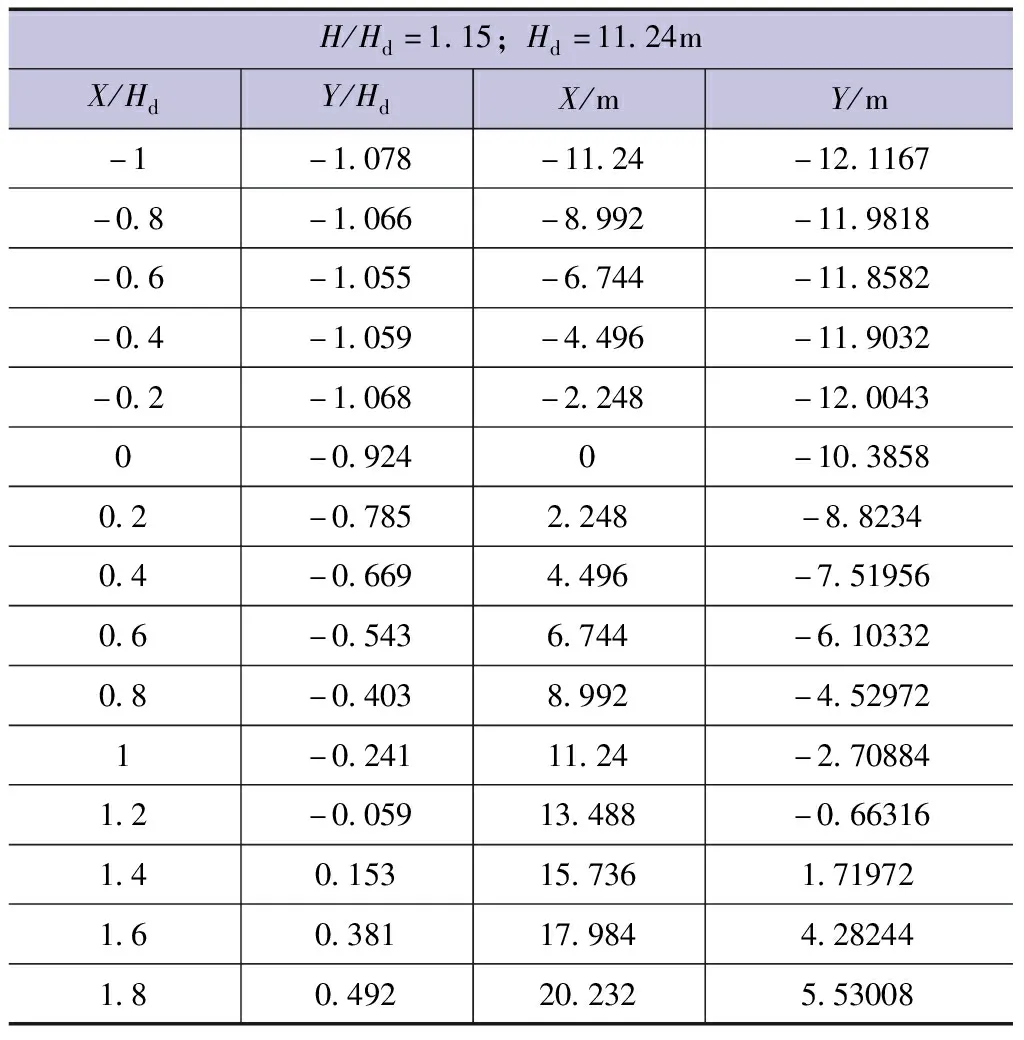
表2 水面线坐标计算数据
1.3.3 反弧段水深
坎顶水深h=q/v=118.7/19.084=6.22m。
1.3.4 溢流坝段边墙高度的确定
《混凝土重力坝设计规范》(DL 5108—1999)规定,中间直线段较短,堰顶曲线边墙高度,采用在自由水面线以上1.5m处,反弧段边墙高度在挑坎水深以上1.2m。
1.4 溢流坝剖面设计
那坡水库重力坝中采用WES曲线,大体可以分为顶部曲线段、直线段和反弧段。
1.4.1 顶部曲线段
溢流堰的曲线采用WES型曲线,基本剖面形状见图1,其中Hd为设计水头,取75%~95%堰顶最大水头(Hmax)。
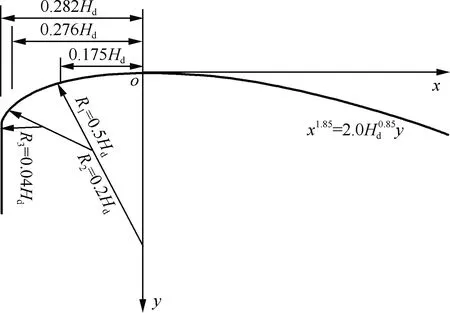
图1 WES型堰面曲线
以曲线的顶点为坐标原点建立x和y坐标轴,分别用三圆弧法和WES绘制图像,计算公式如下:
x1.85=2.0Hd0.85y
(5)
式中Hd——堰顶设计水头,取Hd=0.87Hmax=11.24m。
溢流堰上游段及三段圆弧的尺寸,见表3。

表3 三段圆弧参数值
溢流堰下游段:x1.85=2.0×130.85y。
堰面曲线坐标见表4。
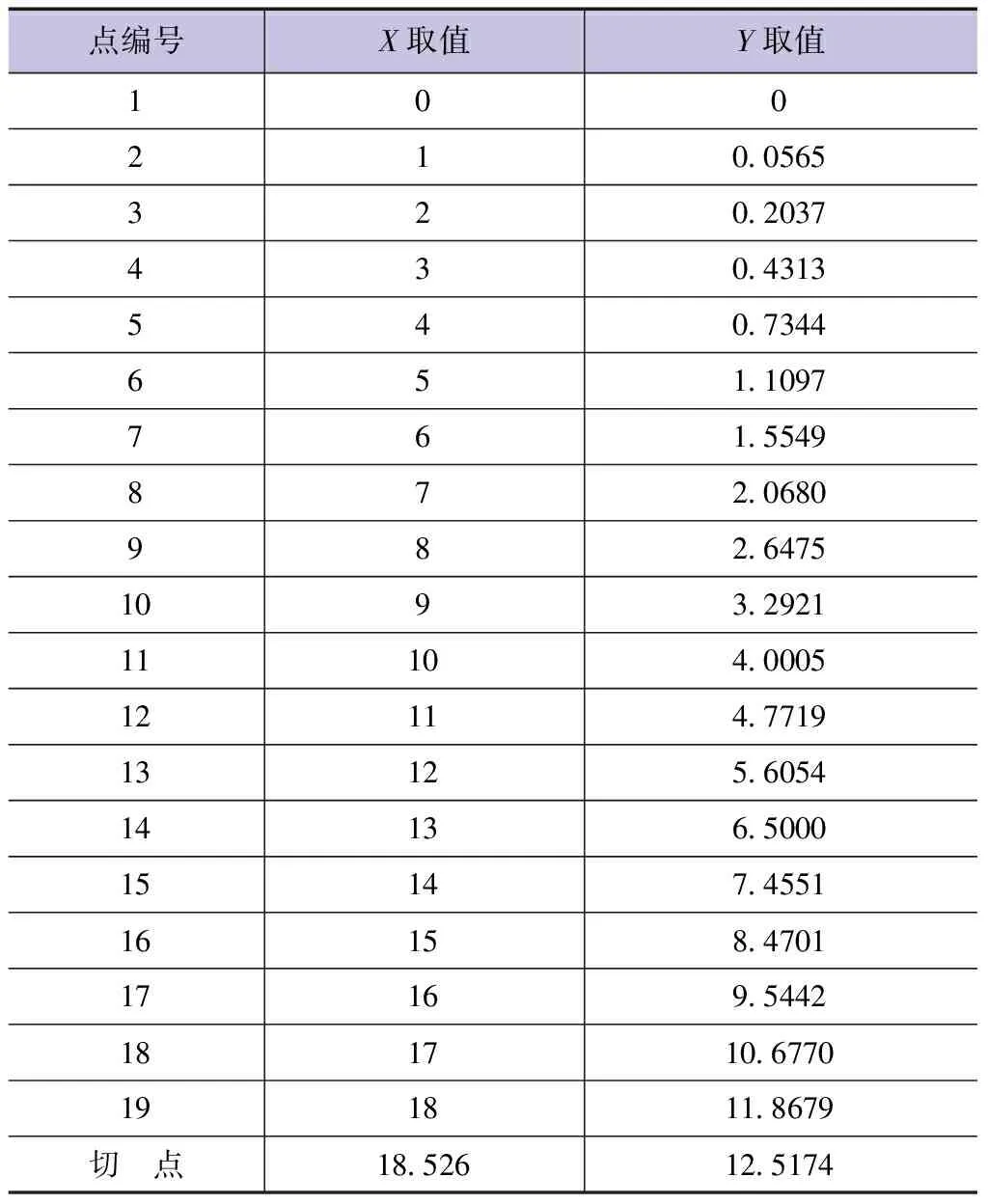
表4 WES曲线坐标
1.4.2 中间直线段
非溢流坝段下游坡率等于溢流坝直线段坡率,m=1∶0.8。
2 数值模拟分析
基于有限体积法利用FLUENT软件建立气水两相湍流模型[4-5],对那坡水库水库溢洪道过坝水流进行三维数值模拟,对校核洪水位及设计洪水位工况下的流速分布及水面线进行验证(见表5)。

表5 模拟工况
a.图2、图3分别为校核洪水位和设计洪水位工况下,溢洪道0+000、0+005、0+020三个断面的流速矢量分布,流速方向如箭头所示。从断面矢量上看,流速由堰顶向挑流坎逐渐增大,挑流坎末端最大流速约为24.41m/s,堰顶最大流速约为12.12m/s,与理论计算值对比拟合度较高。弧段最低点前高速流区位于上层,最低点后高速流区位于下层。与理论计算流速的平均值对比,模型可以模拟水流在纵向断面上的流速分布,从而对设计值进行验证,有针对性地加强溢洪道局部位置的抗冲刷能力。

图2 校核洪水位下流速分布矢量图

图3 设计洪水位下流速分布矢量图
b.水面线拟合分析。通过数值模拟得到的水闸上游及溢洪道上水面线分布见图4,图中点状标识代表理论计算数值,对比分析发现,水闸进口断面处模拟值比理论计算值高0.121m,最大水面线差值为ΔHmax=0.78m,最小差值为ΔHmin=0.02m,经分析,最大最小差值出现断面均为0+018.21处,对比两种工况发现,工况B模拟拟合度最高,差值最小,工况A模拟拟合度最低,差值最大,但两种工况下总体拟合度均较高,误差均控制在0.72%以内,数值模拟具备较高的参考及指导意义。

图4 不同工况模型数值计算及水面分布
3 结 论
本文通过对那坡水库溢流坝段进行设计,确定定型水头,计算不同设计水头堰顶最大负压,利用消能防冲计算确定溢洪道反弧半径及挑流鼻坎的挑角,通过溢洪道水面线计算及剖面设计确定了溢洪道边墙高度及WES曲线顶部曲线段、直线段和反弧段构造。溢洪道数值模型计算结果符合基本理论紊流模型,较全面地模拟计算了溢洪道在校核洪水位和设计洪水位下的典型断面的三维速度场和水面线分布,模型模拟与理论计算值对比结果表明,本文建立的模型能较准确地模拟那坡水库溢洪道的流场分布和水动力特性,为溢洪道可研阶段设计合理性提供更为可靠的数据支撑。
