改进的窗参数优化S变换及其在河道检测中的应用

张付瑷 陈学华* 罗 鑫 张 杰 徐 赫

(①成都理工大学油气藏地质及开发工程国家重点实验室，四川成都 610059；②成都理工大学地球勘探与信息技术教育部重点实验室，四川成都 610059)

0 引言

时频分析方法[1]是一种时变非平稳信号处理方法，它对信号进行时频分析处理，得到时频域信号的能量分布，是地震资料精细构造解释和储层预测的有力工具。

基于傅里叶变换的时频分析方法发展很快，如：Gabor[1]提出的短时傅里叶变换；Morlet等[2]提出的小波变换；Stockwell等[3]结合前两种方法的优点提出的S变换。但上述方法受到自身固有的测不准原则所限，时频分辨率无法达到很好的效果，为了达到最佳效果，研究人员又提出了各种改进的时频分析方法。陈学华等[4]提出广义S变换，引入了λ和p两个参数共同控制窗函数，相比S变换具有更好的适应性和更高的时频分辨率；Lu等[5]基于零相位自适应鲁棒滤波器提出了一种加窗Hilbert变换；Gholami等[6-7]利用混合范数稀疏性，提出稀疏短时傅里叶变换；Sattari等[8-9]考虑到地震数据频率的迅速变化，提出了一种新的基于快速稀疏的S变换。这些改进的方法使时频分辨率得到较大的提升，并且广泛应用于地震资料低频阴影分析、断层识别、弹性参数反演和河道检测等[10-12]。在实际应用中取得的效果证明了时频分析方法的有效性。高静怀等[13]将广义S变换应用于薄互层模型分析；陈学华等[14]利用高阶伪希尔伯特变换对河道、断层等不连续信息进行预测；对于依赖频率的AVO反演，时频分析方法则直接影响反演结果的分辨率[15-16]。此外，在流体流度属性的提取中，高精度时频分析方法也有广泛应用[17-21]。

随着地震勘探技术不断发展，地震资料解释的精度要求越来越高，需要利用更加有效的时频分析方法从地震数据中提取有效信息。因此，进一步改进和发展高分辨时频分析方法仍是开展地震资料精细储层描述的关键环节。本文在窗函数优化S变换[9]的基础上，提出通过引入新的窗函数调节参数，构建改进的窗参数优化S变换方法，能够根据实际信号的振幅谱自适应地求取最优窗参数，得到的时频谱具有更高的时频聚焦性和分辨率。通过合成信号对比分析，验证了该方法在低、高频端均具有较高分辨率；在实际地震资料的河道检测中能更好地刻画河道的空间展布特征，显示的地质细节特征更清晰，利于地震资料的精细解释。

1 方法原理

Stockwell等[3]首次提出了时频分辨率随频率变化的时频表示方法——S变换。它所选取的窗函数随频率的增加而自适应地调节时窗宽度。在S变换中，高斯窗函数的表达式为

(1)

式中：t为时间；σ为窗函数的调节尺度参数。

为了使窗函数随频率变化，定义σ为随频率f变化的函数，即

(2)

S变换的窗函数会根据频率的增加而减小时宽，但在时域压缩的同时会在频域拉伸，存在时间分辨率和频率分辨率不相容的问题。Sattari等[9]在S变换的基础上，提出窗参数优化S变换，将传统S变换中仅随时间或频率变化产生最优窗的问题转化为一个二维的问题。通过优化的窗函数定位局部的强振幅频率分量，并对弱振幅频率分量进行模糊处理，从而控制二者在时频谱上的影响区域。由于振幅谱中包含了频率和振幅的信息，因此将其作为优化窗函数的参照。基于上述思想，本文设计了根据实际地震信号的振幅谱自适应确定最优窗参数的流程，并基于求取的最优化窗参数构建了改进的窗参数优化S变换方法。优化流程如下。

(1)对原始信号x(t)求取振幅谱

X(f)=abs{FT[x(t)]}

(3)

式中FT表示傅里叶变换。

(2)对振幅谱X(f)进行平滑处理

Xs(f)=smooth[X(f)]

(4)

(3)保证平滑后的结果均大于0，即

(5)

(4)归一化

(6)

(7)

式中r为可调节参数。通常对于带限信号，r取1或2；对于地震信号，r取3或4；对于带宽信号，r取5～10。

(6)求得随频率变化的最优窗参数

(8)

式中N表示离散信号点的个数。

通过r优化后的窗参数优化S变换，使信号时频聚焦性和分辨率有了一定的提高，但仍有改进的空间。之后引入λ、p(λ>0,0.5≤p≤1.5)两个参数，共同调节窗参数s(f)。在实际应用中，根据实际信号的特征灵活选择λ、p，当λ取值过大时，可适当调整p值，从而得到最佳的窗参数。

λ、p两个参数的进一步优化，使改进后的调节参数可以根据实际应用中非平稳信号的频率分布特点和时频分析的侧重点，调节窗函数随频率变化的速度，能够灵活地适应具体信号。

进一步构建出改进的窗参数优化S变换的调节参数为

(9)

由此得到改进的窗函数

(10)

得到改进的窗参数优化S变换表达式

(11)

式中τ为窗函数中心点，控制窗函数在时间t上的移动。

图1显示不同处理流程对窗参数的优化效果。图1a为合成信号时域波形，对合成信号分别做S变换、窗参数优化S变换和改进的窗参数优化S变换，并与信号的振幅谱(图1b)进行对比。由图可以看出，窗参数的变化具有对称性，其中S变换的窗参数呈线性变化(图1c)，进行优化后的窗参数随信号振幅谱自适应变化(图1d)，本文方法对优化的窗参数又有进一步改进，得到的窗参数能够更好地适应信号的突变(图1e)。

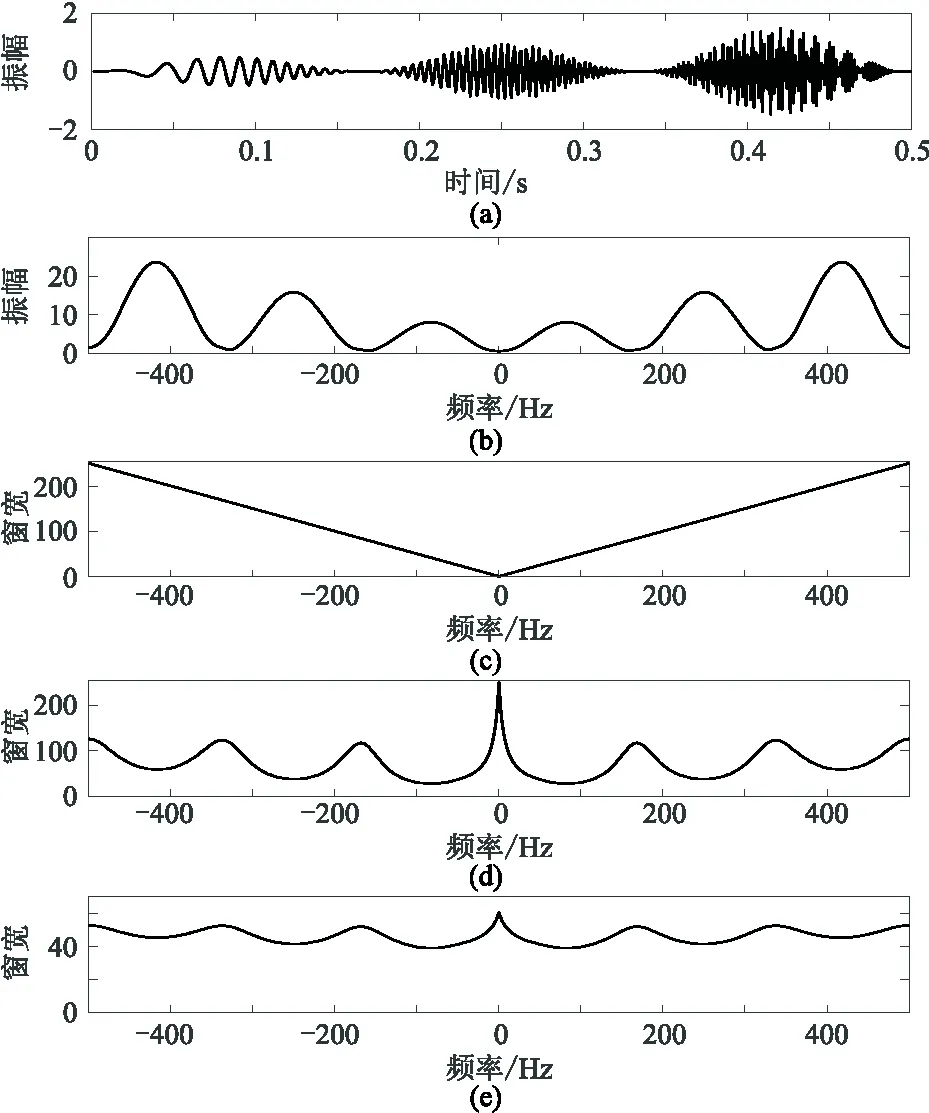
图1 信号振幅与不同处理方法窗宽的关系

优化后的窗函数可以根据实际信号的振幅区分不同的频率分量，同时在时间和频率域也具有自适应性。λ和p两个可调节参数的引入，使变换处理更具灵活性，时频聚集性更好，对非平稳信号中的各种分量区分能力更强，因而该方法得到的时频谱具有较高的时频分辨率。此外，当λ=1、p=1时，该方法即等价于窗参数优化S变换。

2 模型试算与分析

为了便于分析本文方法的效果，设计了一个合成的非平稳信号进行模型试算。信号由两个不同频率成分的Chrip信号组成(图2a)。对该信号分别做S变换、窗参数优化S变换(r=10)和改进的窗参数优化S变换(r=10，λ=6，p=0.5)，分别得到对应的时频谱(图2b～图2d)。对比可知，窗参数优化S变换(图2c)相比S变换(图2b)具有更高的频率分辨率，尤其在高频部分优势更加明显，原因在于窗参数优化S变换在S变换的基础上对强振幅频率分量进行了适应性调节，因此得到的时频谱分辨率更高，聚焦性更好。而相比窗参数优化S变换的结果，改进的窗参数优化S变换(图2d)不仅在高频端保持了很高的分辨率，在低频端分辨率也有明显的提升，能够更清楚地分离两个不同频率分量的信号，说明本文方法具有更强的信号区分能力。

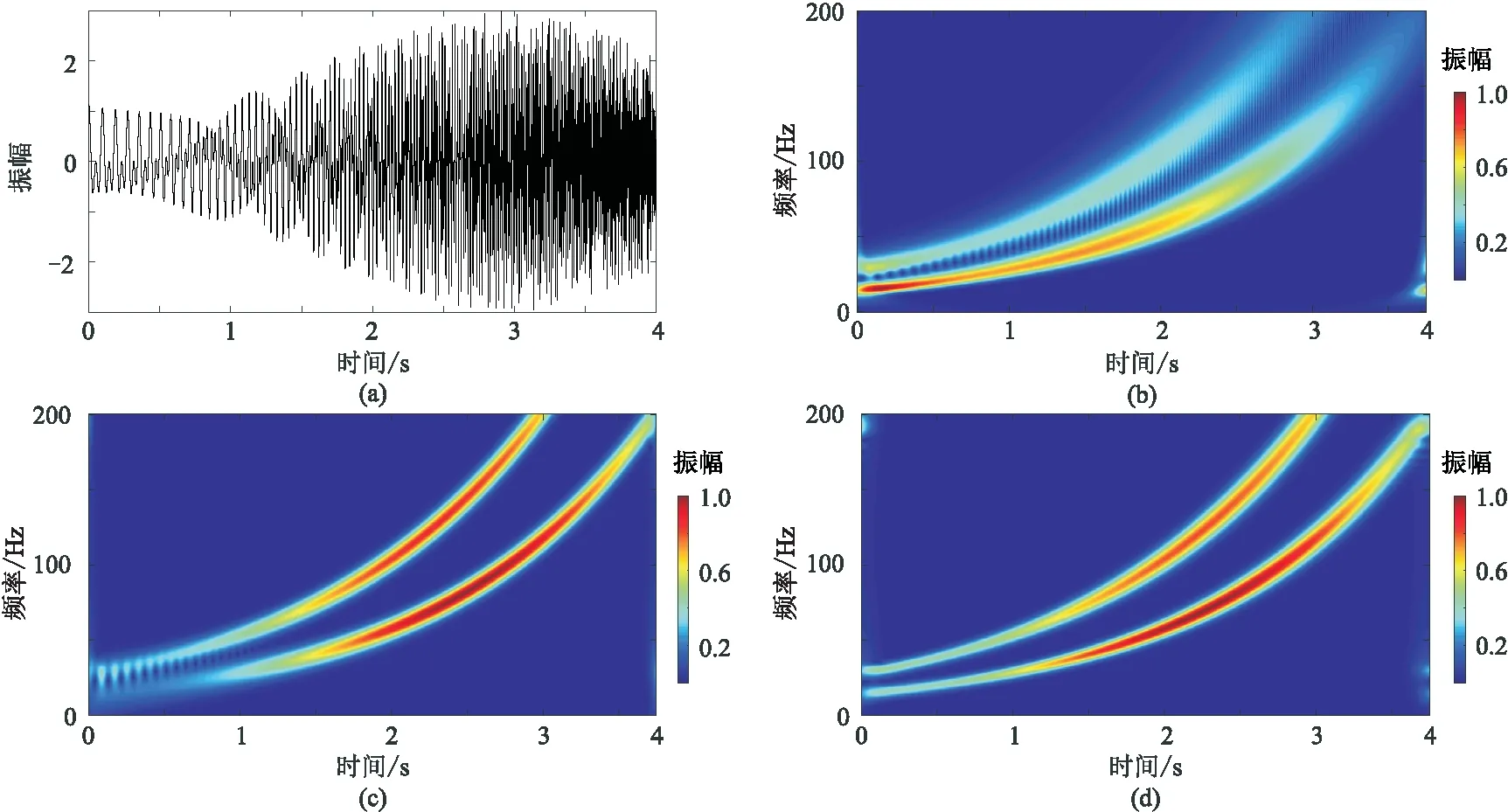
图2 合成的Chrip非平稳信号及不同方法处理的时频谱

3 实际地震资料处理

将本文方法应用到某海上工区的实际地震资料处理。图3a为工区内提取的原始地震剖面(图中蓝色线为解释的目的层)，对地震数据分别做S变换、窗参数优化S变换(r=3)和改进的窗参数优化S变换(r=3，λ=8，p=0.5)后，抽取40Hz的共频率剖面进行对比分析。由图3可见，改进的窗参数优化S变换得到的共频率剖面(图3d)分辨率更高，并且具有很好的横向连续性，可以更好地表现地震记录随时间的变化。说明本文方法在提升时频聚焦性和时频分辨率方面效果更佳，能更好地适应非平稳信号的突变。

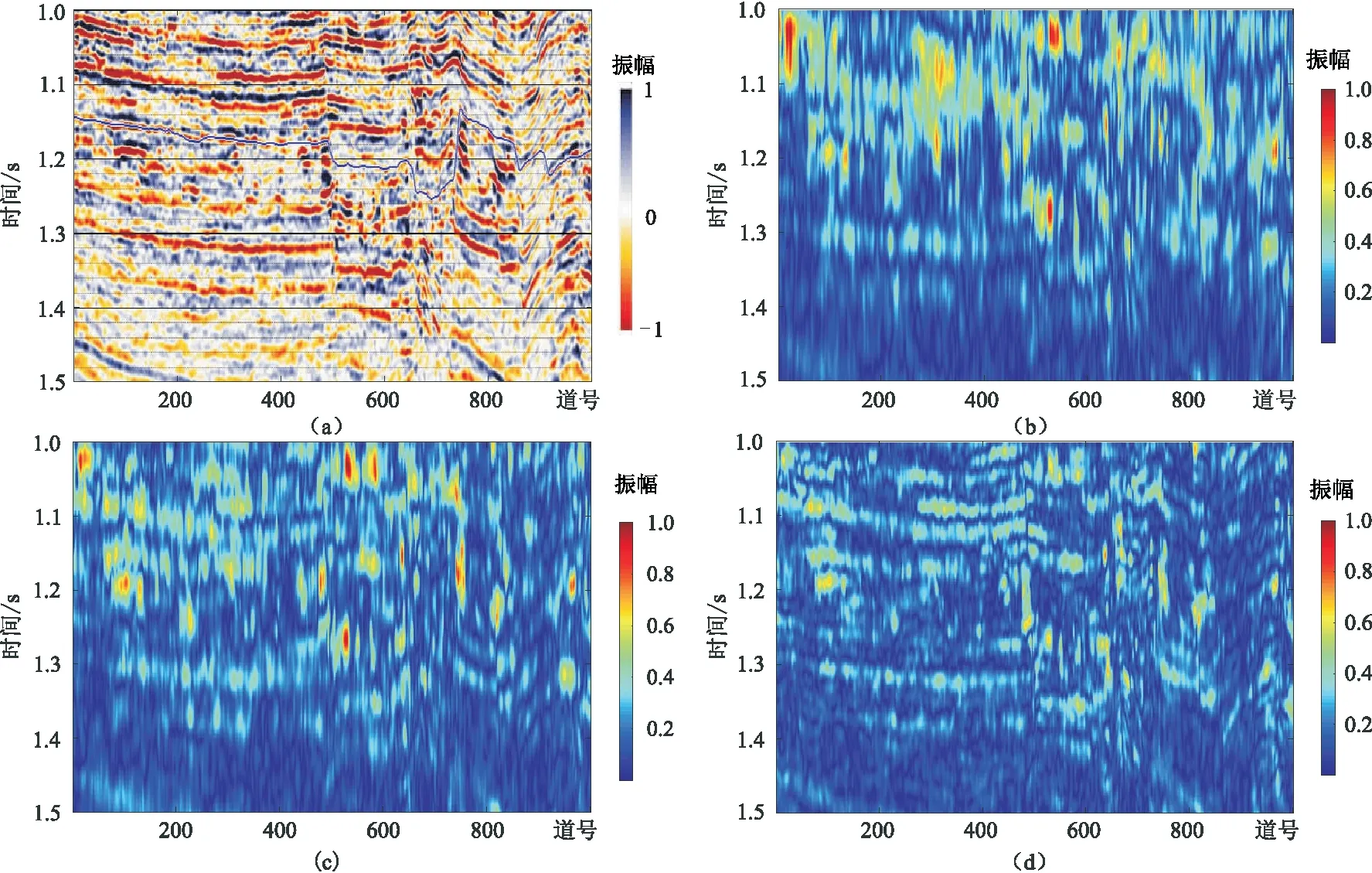
图3 原始地震剖面及不同方法处理后的40Hz共频剖面

从图3所示剖面中抽取第500道地震记录进行单道时频分析，结果显示，本文方法S变换结果同样显示出更好的时频聚焦性和更高的分辨率，频谱能够更加清晰地反映地震记录的变化(图4d中红色虚线框标识处)，说明改进的窗参数优化S变换在实际应用中更具优势。

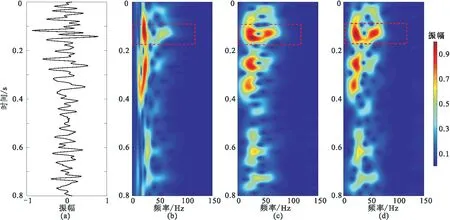
图4 单道地震记录及其不同方法处理的时频谱

为进一步说明本文方法的实用性和优越性，将上述三种S变换方法应用于整个工区三维地震数据体处理。图5为原始地震数据体中抽取的沿层切片(图中黑线为图3选取的剖面位置)。由图可见，该地区河道较为发育，但是切片上显示的河道特征比较模糊，难以获得有效的细节信息。分别采用不同方法对三维数据进行瞬时谱分解，然后从不同方法处理得到的40Hz数据体中抽取沿层切片，进行河道特征分析。结果显示，在常规S变换(图6a)和窗参数优化S变换(图6b)结果中,能够显示出较大尺度的河道(图中黄色矩形虚线框所示)，但是背景比较模糊；在本文方法处理的结果中，除了清晰显示较大尺度的河道外，还能见到一些更小细节的河道(图6c中红色椭圆虚线框所示)。此外，从图6c中还观察到一些隐蔽的河道(图中橙色箭头所示)，而该特征未在图6a和图6b中清晰显示。说明改进的窗参数优化S变换结果能够更加清晰地显示河道的形态和分布，刻画更多的细节特征。图6d为应用本文方法对数据体进行分频处理后，对40、60、80Hz的单频振幅谱进行RGB融合[22-24]得到的切片。图中同样显示出了隐蔽河道的位置和细节，且更为清晰。

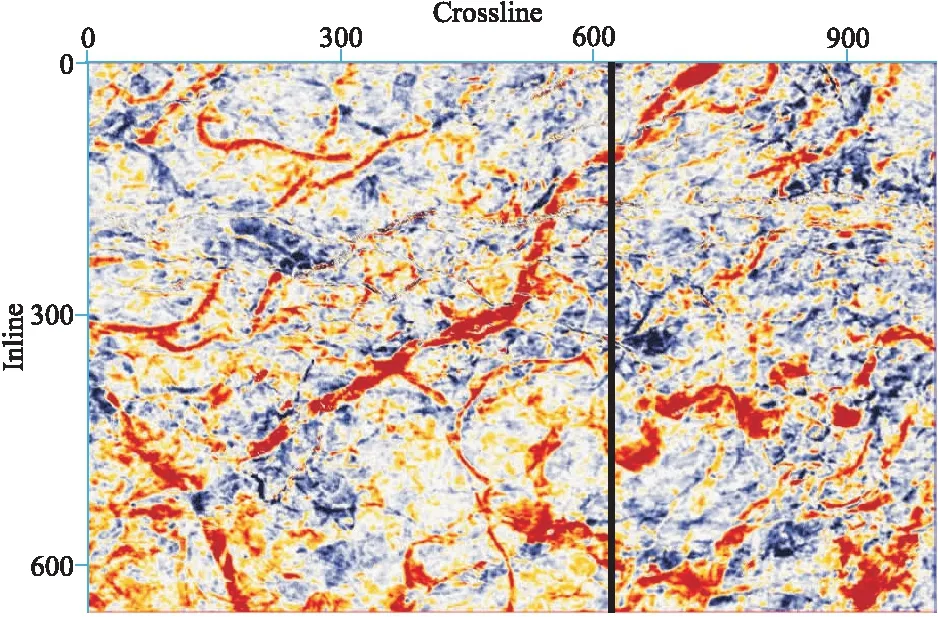
图5 原始地震数据沿目的层的振幅切片

图6 不同方法处理数据体抽取的沿层切片

4 结论

本文基于窗参数优化S变换，通过引入新的调节参数，构建了一种改进的窗参数优化S变换方法，合成信号和实际资料的应用结果均表明该方法具有时频分辨率高和能量聚集性好的优势。在三维地震资料的河道检测中，改进的窗参数优化S变换的处理结果效果更好，能够更清晰地刻画出河道的形态，显示河道的连续性，为地震资料精细储层描述提供了有力的技术支持。此外，该方法在地震属性分析、弹性参数反演等方面也具有良好的应用前景。