应用加权迭代软阈值算法的高分辨率Radon变换

薛亚茹 郭蒙军* 冯璐瑜 马继涛 陈小宏

(①中国石油大学(北京)信息科学与工程学院，北京 102249； ②中国石油大学(北京)地球物理学院，北京 102249)

0 引言

奥地利数学家Radon于上世纪初提出了Radon变换理论，经过不断的发展完善，逐渐从数学领域沿用到其他领域。Claerbout等[1]将Radon变换引入地震勘探领域，极大地促进了Radon变换在地震资料处理方面的应用，如多次波压制、缺失地震道重建、平面波分解以及去噪，且该变换可在时域、频域及混合域实现。

由于线性Radon变换和抛物Radon变换具有时不变特性，故可在频域快速求解。Hampson[2]提出抛物Radon变换并将其应用于多次波压制，且在频域用最小二乘(Least square，LS)算法求解，但该方法的分辨率并不高； 之后，Sacchi等[3-4]结合贝叶斯原理，通过引入模型的先验信息提高Radon变换的分辨率。由于高分辨率Radon变换迭代过程涉及矩阵求逆运算，导致其计算量较大，为此采用低频约束方法，即用上一频率计算结果约束当前频率的计算[5-6]。刘喜武等[7]利用稀疏约束共轭梯度算法求解Radon变换，与阻尼LS算法相比，提高了Radon变换的分辨率和计算效率； 王维红等[8]提出基于Levinson递推法的加权抛物Radon变换叠前地震数据重建方法，与传统的高分辨率Radon变换方法相比，计算效率有所提升； 薛亚茹等[9]将传统抛物Radon变换与正交多项式相结合，克服了空间假频，并保留地震波的AVO特性； 之后，王亮亮等[10]在此基础上引入新变量，消除了变换算子对频率的依赖，提高了计算效率。由于L1范数不具有真正意义上的稀疏性，薛亚茹等[11]引入SL0范数约束，并通过最速下降法和梯度投影原理实施了高分辨率Radon变换。

由于Radon模型在时域比在频域更具有稀疏性，Cary[12]和Schonewille等[13]在时域实现了Radon变换，提高了其分辨率，但收敛速度较慢； 巩向博等[14]提出各向异性Radon变换，通过最优相似系数加权Gauss-Seidel迭代算法，提高了Radon变换计算效率。结合Radon变换在时域的稀疏性及在频域的计算高效性，Trad等[15]在频域实现Radon变换的正向和反向过程，并利用迭代加权最小二乘法(Iterative reweighted least square，IRLS)在时域求解稀疏Radon变换，充分兼顾时域Radon变换和频域Radon变换的优点； 此后，Lu[16]用迭代收缩算法(Iterative-shrinkage algorithms)代替IRLS，进一步提高混合域Radon变换的计算效率； 在此基础上，Wang等[17]针对噪声偏离高斯分布的Radon变换，引入Bregman方法，提高了混合域Radon变换的鲁棒性； 巩向博等[18]在混合域实现双曲Radon变换，并引入快速迭代软阈值算法(Fast iterative shrinkage-thresholding algorithm，FISTA)加快反演收敛速度。随着Radon变换在地震数据领域的更广泛应用，近年来还研发出基于字典学习的用于去噪和插值的Radon变换，通过稀疏表征地震数据并结合K-SVD方法实现求解[19-21]。由于高分辨率Radon变换计算量较大且计算结果易受正则化影响，也有学者提出在压缩感知框架下处理地震数据，利用匹配追踪等算法，以提高地震数据处理的计算精度和效率[22-26]。

本文分析了迭代软阈值法(Iterative soft threshold algorithm，ISTA)和IRLS实现Radon变换的基本原理，提出将IRLS的加权矩阵思想引入ISTA方法中，形成加权迭代软阈值法(Reweighted-Iterative soft threshold algorithm，R-ISTA)，以进一步提高Radon变换分辨率。

1 方法原理

1.1 Radon变换反演基本原理

在地震勘探领域，常用的Radon变换有线性Radon变换、抛物Radon变换和双曲Radon变换。抛物Radon变换将动校正后的同相轴沿时距曲线进行叠加，得到Radon参数。由于采集到的地震数据为离散数据，一般采用离散Radon变换，Radon正变换离散形式为

(1)

式中：m为Radon域数据；d为时空域地震数据；q为曲率参数；h为炮检距；t为时间；τ为时空域双重旅行时截距；Nq为Radon域曲率参数个数。

抛物Radon变换具有时不变性，可将其变换到频域进行计算，以提高计算效率。对式(1)做傅里叶变换得到对应的频域Radon正变换公式

(2)

可写成如下矩阵形式

D=LM

(3)

其中Radon变换算子矩阵L的具体表达式为

(4)

式中Nh为道数。

由于矩阵L通常不是方阵，无法求逆，其LS解分辨率低，基于L1范数的稀疏正则化是现今常用的高分辨率反演方法。构造高分辨率反演目标函数为

(5)

式中λ为拉格朗日因子，且有λ>0，用于平衡模型的准确度和稀疏性。ISTA是上述优化问题常用求解方法之一[27-30]，该算法求解过程不涉及矩阵求逆，计算效率高，每次迭代过程中经矩阵乘法后通过软阈值函数逐渐逼近所求变量，其迭代式为

Mn+1=Sσ[Mn+ηLH(D-LMn)]

(6)

式中：n为迭代次数；η为正参数，通常取为LHL最大特征值的倒数；Sσ为软阈值函数，其表达式为

Sσ(M,σ)=sign(M)max{0,|M|-σ}

(7)

式中： sign为符号函数；σ为阈值，该值与上一次迭代结果有关，即达到自适应阈值的目的，其经验表达式为

σ=0.01 max(|Mn|)

(8)

由于矩阵L具有非正交性，式(6)中共轭算子LH降低了Radon变换的分辨率，使得上述算法应用于Radon变换反演时收敛速度较慢。

1.2 基于R-ISTA算法的高分辨Radon变换

IRLS是高分辨Radon变换的另一种常用方法[31]。Sacchi等[3-4]基于贝叶斯原理，将模型先验信息与Radon变换相结合，将前一次迭代结果作为下一次反演的加权矩阵； 经过若干次迭代之后，得到高分辨率的Radon变换。

据式(3)构造如下目标函数

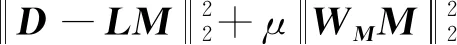
(9)

式中：μ为阻尼因子，取值范围是0.01～1.00；WM为数据M的协方差矩阵。将式(9)最小化，可得

M=(LHL+μW)-1LHD

(10)

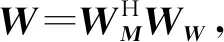
为克服ISTA中Radon共轭算子分辨率低的问题，引入IRLS的Radon变换中权重矩阵思想，将IRLS的加权反演矩阵引入ISTA中，得到R-ISTA公式，即改进的式(6)表达式

Mn+1=Sσ{Mn+ηB-1[LH(D-LMn)]}

(11)

与式(6)所示传统的ISTA公式相比，本文引入与加权矩阵相关的反演矩阵

B=LHL+μW

(12)

式中对角矩阵W的对角元素与前一次迭代Radon域数据M有关，用来聚焦Radon域能量，即

(13)

式中b是稳定因子。

与传统ISTA方法相比，本文所提R-ISTA方法通过引入权重矩阵使Radon域能量聚焦，当上一次迭代得到的Radon域数据M部分能量较低时，则相应的权重矩阵较大。类似地，当前一次迭代得到的M数据部分能量较高时，其对应的权重矩阵较小； 随后经矩阵求逆运算，使得数据M中能量强的部分继续加强，能量弱的部分进一步减弱，以此达到高分辨率Radon变换的目的。

1.3 基于主频约束的R-ISTA高分辨Radon变换

迭代加权方法对每个频率都需计算反演权重矩阵(式(12))，还需做求逆运算，故计算量较大。为了降低运算耗时，可用单个频率的运行结果约束其他频率，避免逐个分别对每一频率计算权重矩阵，这样就可提高Radon变换计算效率[5-6，32]。

为提高R-ISTA的计算效率，本文设计了适用于多次波压制的主频约束R-ISTA。首先选取地震数据的主频进行迭代训练，在分辨率达到要求后停止迭代，并保存其迭代得到的最终权重矩阵，然后用该频率训练得到的权重矩阵去约束其他所有频率的反演。基于主频约束的R-ISTA迭代公式为

(14)

式中Bmain为定值，不随迭代次数变化，其表达式为

Bmain=LHL+μWmain

(15)

式中Wmain为主频训练迭代得到的加权矩阵，此后其值不再随频率变化。由于只需进行一次求逆运算，所以计算量大幅度减少。

基于主频约束的R-ISTA压制多次波的步骤如下：

(1)设置初始参数，通过傅里叶变换把时空域地震数据d变换到频域D=F(d)；

(2)选择主频对应的频域数据Dmain，利用式(11)获得该主频的Radon参数，保存其加权参数矩阵Wii=(|Mi|2+b2)-1，以此约束其他频率的反演；

(3)对频域所有地震数据D，由LS计算其迭代初始值M0=(LHL+μI)-1LHD； 将M0代入主频约束R-ISTA迭代式(式(14))，其中伪逆矩阵由式(15)计算，迭代至收敛，得到Radon域数据Mn；

(4)在Radon域分离一次波与多次波，实现多次波压制。

2 数据实验

2.1 模拟数据

为比较ISTA、IRLS及R-ISTA三种方法实现Radon变换的分辨率及压制多次波的效果，构建如图1a所示的模拟地震数据：采用主频为30Hz的Ricker子波，采样点数为200，采样间隔为4ms，共计64道； 共含4条同相轴，其中一次波(图1b)和多次波(图1c)各两条。针对图1a模拟数据对应的原始Radon数据(图2)，分别用ISTA、主频约束IRLS及主频约束R-ISTA三种方法进行处理，反演得到对应的Radon域数据(图3a～图3c)及其与原始Radon域数据的误差(图3d～图3f)。其中：ISTA和主频约束R-ISTA的迭代次数为10； 主频约束IRLS的主频迭代也为10次，其他频率反演无需迭代。

图1 模拟地震数据

图2 原始Radon域数据

观察、对比可见：ISTA反演得到的Radon域数据能量较分散，分辨率较低，无法分离剩余时差差异较小的两同相轴； 主频约束IRLS虽可将其分离，但还是存在能量扩散现象； 而主频约束R-ISTA反演得到的Radon参数能量集中，分辨率高。

进一步分析反演所得结果(图3)，可知一次波与多次波已分离，去除其中一次波，经Radon反变换可得到时域多次波数据，从原始地震数据减去多次波数据，即可达到去除多次波的效果。分别用ISTA、主频约束IRLS和主频约束R-ISTA处理模拟地震数据后，恢复出图4a～图4c所示的多次波数据，用原始多次波数据(图1c)分别减去上述三种方法恢复的多次波数据，得到图4d～图4f所示的(放大了5倍的)多次波残差数据。从原始地震数据(图1a)减去三种方法恢复的多次波数据(图4a～图4c)，可得到三种方法估计的一次波数据(图5a～图5c)及其与原始一次波(图1b)的残差(图5e～图5f，放大了5倍)。

图3 不同方法反演得到的Radon域数据(上)及其与原始数据的差值(下)

从图4d～图4f可观察到，主频约束IRLS和主频约束R-ISTA恢复的多次波更接近于真实值，ISTA恢复的多次波与真实值相差较大。观察图5e～图5f，可发现在一次波同相轴与多次波同相轴相邻位置，ISTA方法的多次波残留明显，且一次波数据有丢失； 主频约束IRLS和主频约束R-ISTA两种方法对多次波压制效果都优于ISTA，但主频约束IRLS方法(图5e)仍残存明显一次波数据； 而图5f中则基本看不到一次波残留，因此主频约束R-ISTA恢复的一次波数据更接近实际一次波数据。

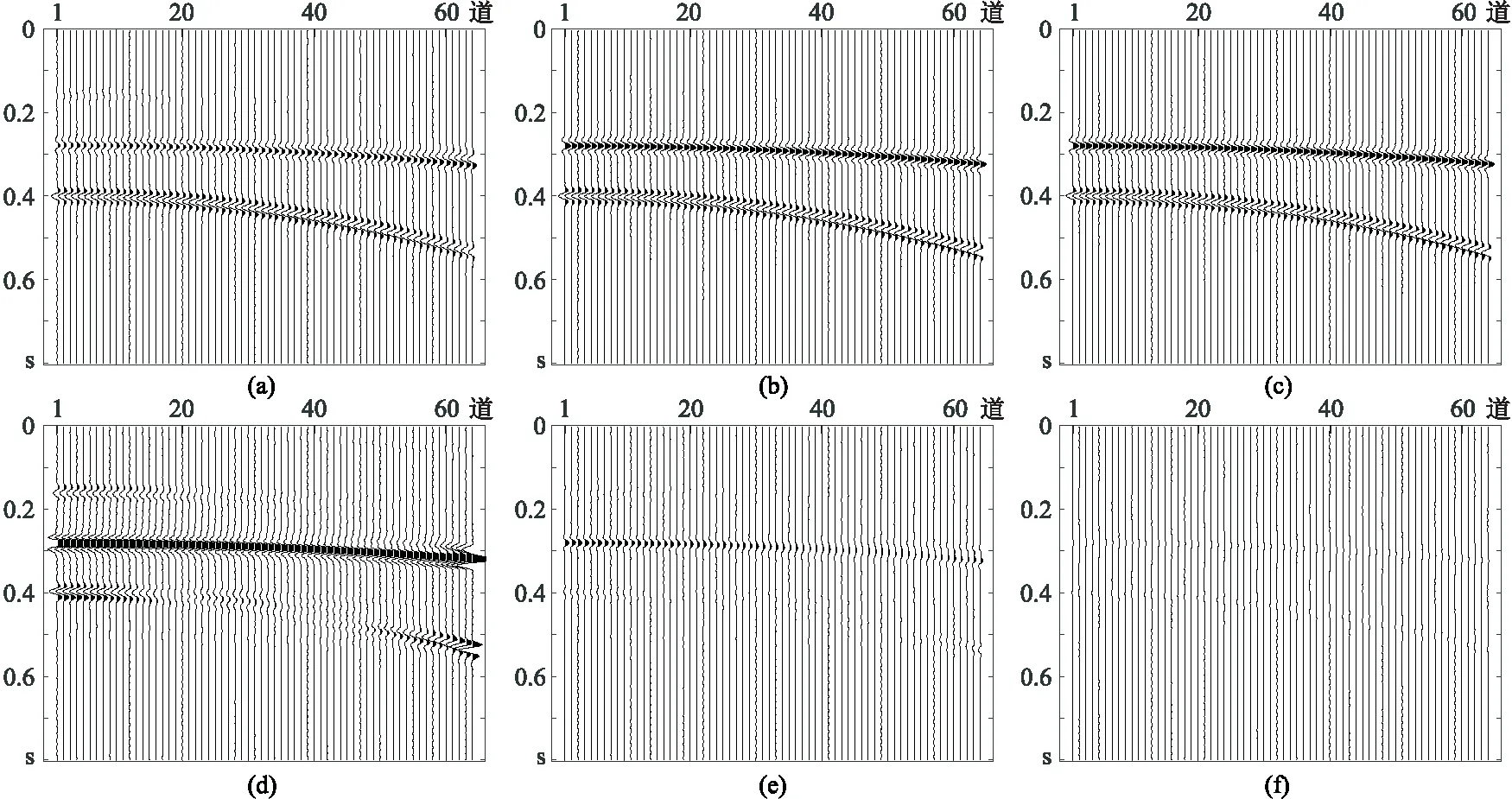
图4 不同方法恢复的多次波数据(上)及其与原始多次波数据的差值(下，放大5倍)

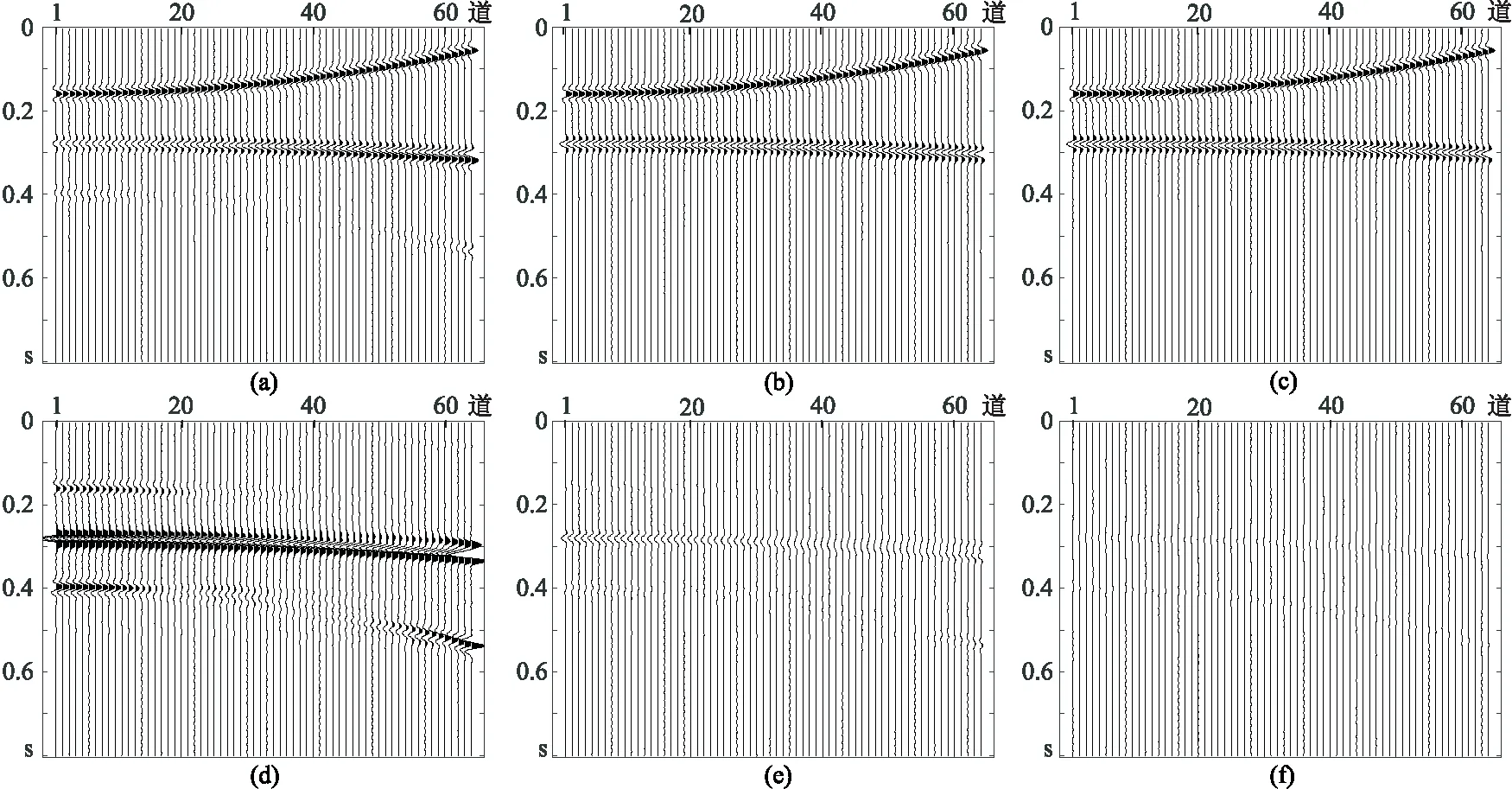
图5 不同方法恢复的一次波数据(上)及其与原始一次波数据的差值(下，放大5倍)

用信噪比衡量不同方法对多次波的压制效果，信噪比定义为

(16)

式中：d为原始一次波数据；dm为不同方法各自得到的一次波数据。本次采用的三种方法所用数据的信噪比如表1所示，可见主频约束R-ISTA得到的信噪比为31.0404dB，远大于ISTA的7.7926dB，同样高于主频约束IRLS的21.6724dB。因此，主频约束R-ISTA对多次波的压制效果优于另两种方法。

为评估R-ISTA的抗噪性能，针对图1a模拟数据加入高斯白噪声，得到图6所示含噪地震数据。根据信噪比定义式(式(16))算出该数据的信噪比为 0dB。分别用ISTA、主频约束IRLS及主频约束R-ISTA压制多次波，得到一次波(图7a～图7c)及其误差数据(图7d～图7f)，三种方法去噪后信噪比见表1。从图7及表1可见，主频约束R-ISTA的去噪效果略优于主频约束IRLS，且都远优于ISTA。

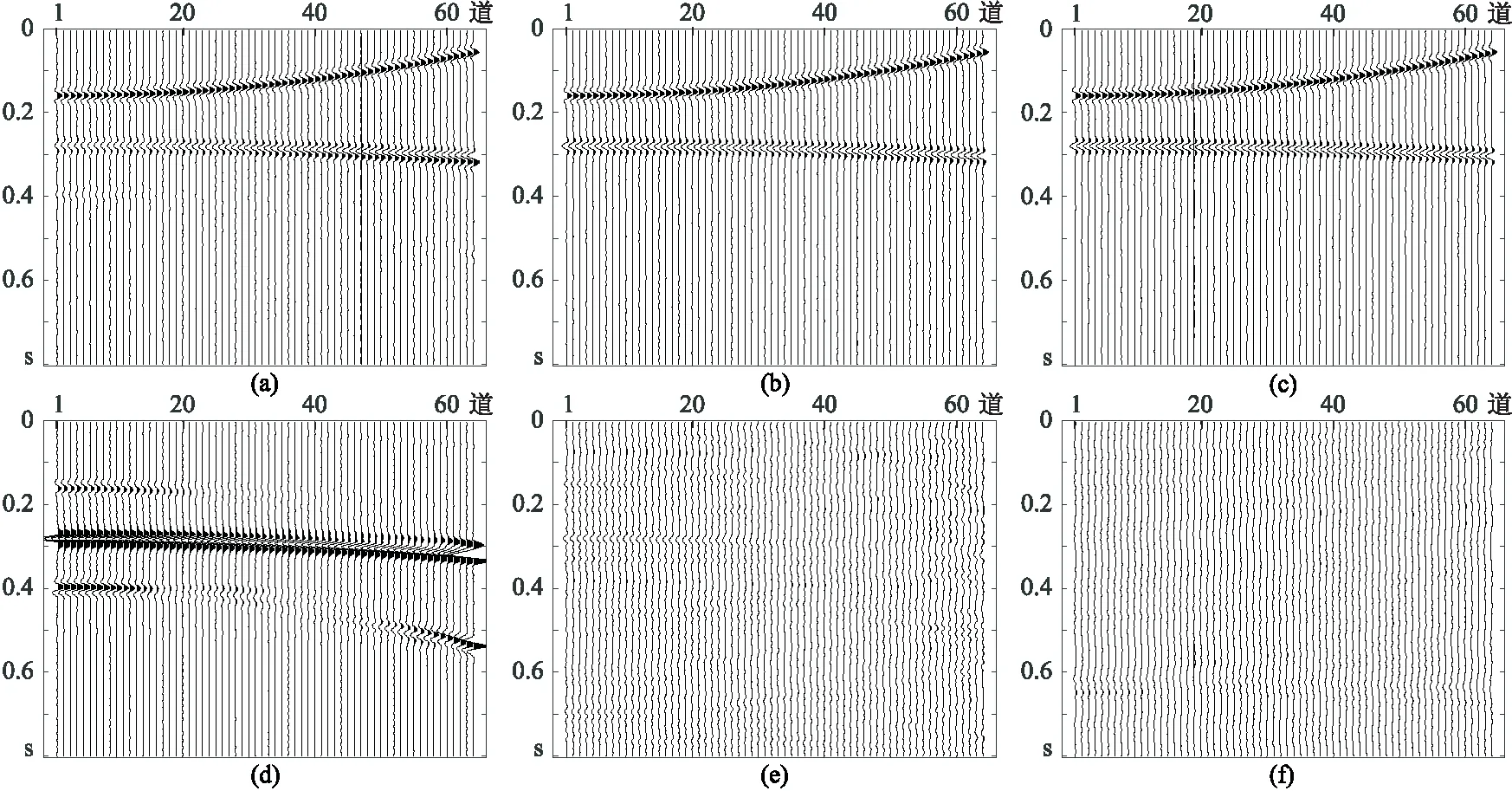
图7 针对含噪地震数据用不同方法恢复的一次波数据(上)及其与原始一次波数据的差值(下，放大5倍)

表1 加噪前后三种方法得到一次波的信噪比

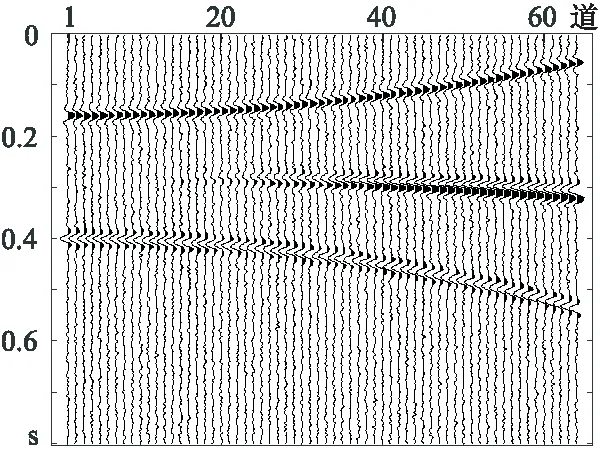
图6 含高斯白噪模拟地震数据

2.2 实际数据

选取M地区三维实际地震数据(图8a)，共计13炮，每炮25道，采样点数为2501，采样间隔为2ms。图8b为对原始数据按炮点距离排序后的实际数据。 经动校正后，一次波同相轴基本被校平，曲率较小， 而多次波仍有剩余时差，曲率较大，故可根据曲率的不同分离一次波与多次波。从图8b可见多次波主要存在于图像中部(红色椭圆)区域，为便于对多次波压制过程做数据分析，选择仅展示图8c所示的中间5炮数据。该数据Radon变换曲率参数q取值范围是-0.4～0.6s。图8d～图8f分别为ISTA、主频约束IRLS和主频约束R-ISTA三种方法反演的Radon域数据，切除0.2s以下部分(黑线左侧区域)，即可获取多次波对应的Radon域数据； 再经Radon反变换得到多次波数据，用原始数据减去多次波数据即可得三种方法压制多次波后结果(图8g～图8i)。

由于从图8g～图8i难以判明三种方法优劣性，故用上述三种方法处理13炮数据后，再按炮点距离排序，得到图9a～图9c所示多次波数据； 进而获得三种方法去除多次波后的数据(图9d～图9f)。其中：ISTA迭代20次； 主频约束R-ISTA迭代5次； 主频约束IRLS的主频迭代10次，其他频率反演无需迭代。观察图8d～图8f中三种方法反演的Radon域数据，可见主频约束R-ISTA求取的Radon域数据比另两种方法更稀疏，去除多次波后可保留更多一次波信息； 从图9d～图9f中箭头所指部分可见，与原始数据相比，经三种方法处理后，ISTA对多次波的压制效果欠佳，另两种方法的压制多次波效果较理想，且主频约束R-ISTA比主频约束IRLS的一次波同相轴更清晰。

图8 实际地震数据

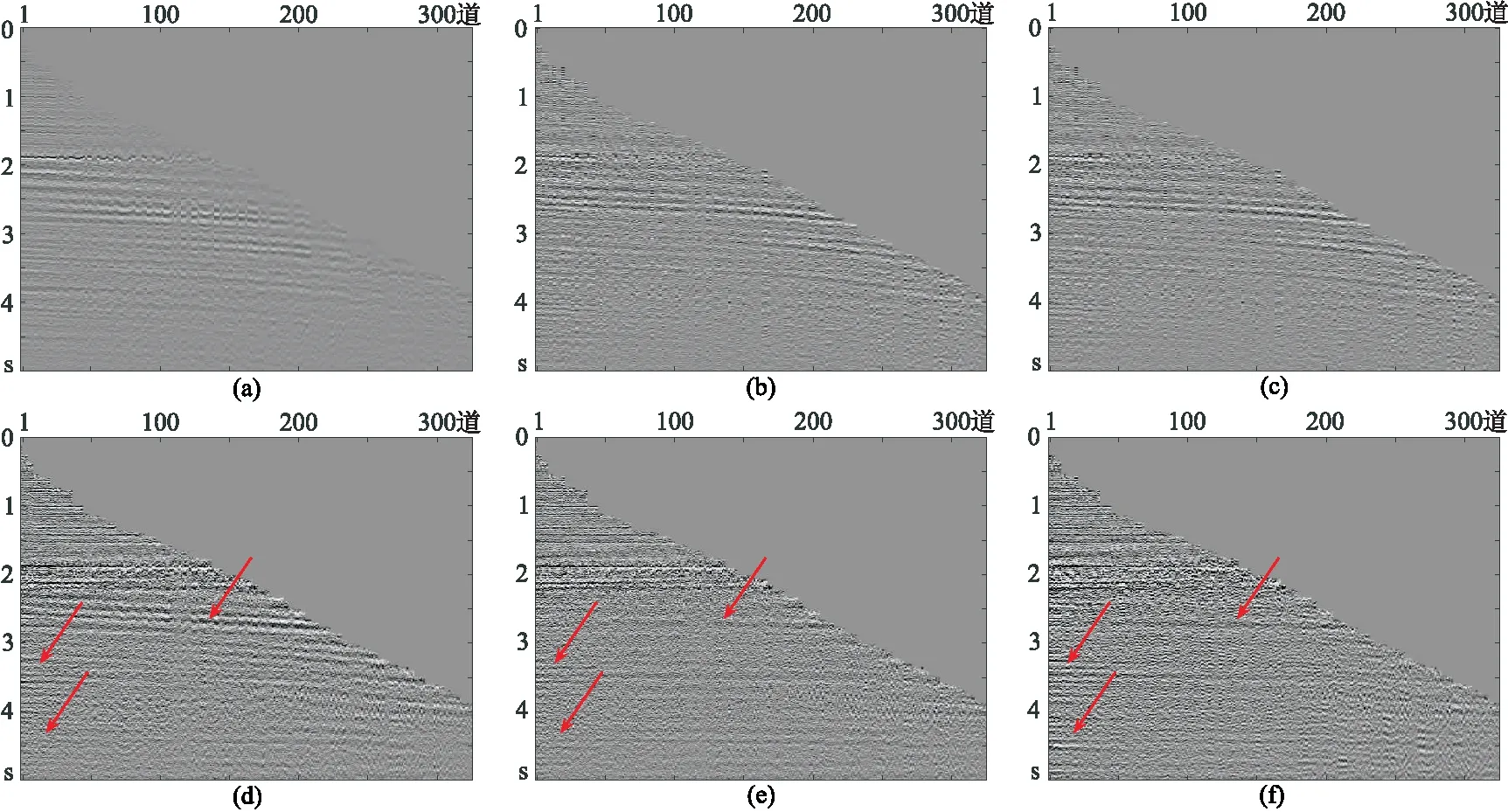
图9 按炮点距离排序地震数据不同方法去除的多次波(上)及剩余数据(下)

2.3 收敛速度

已知ISTA的收敛速度为O1(1/k， 其中k为迭代次数，下同)，即为次线性收敛； FISTA的收敛速度为O2(1/k2)[28]； IRLS为指数收敛[33]。本文以均方误差为收敛性能的评判指标，其表达式为

(17)

将R-ISTA与收敛速度已知的ISTA、FISTA、IRLS及基础的LS对比，得到图10所示的收敛速度图。可见FISTA收敛速度快于ISTA，且此两者的精度略高于LS。迭代初始，IRLS和R-ISTA的收敛速度相差不大，且都快于ISTA； 迭代12次之后，IRLS趋于收敛，R-ISTA的均方误差则继续下降，迭代20次趋于收敛； 最终，R-ISTA的均方误差小于另四种算法。

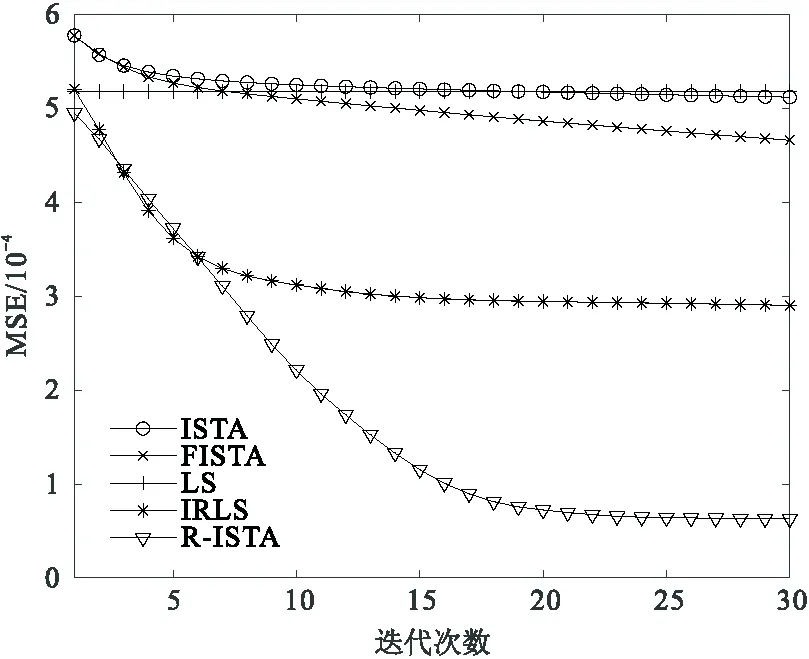
图10 ISTA、FISTA、LS、IRLS、R-ISTA收敛速度

从表2可见，对于相同迭代次数(1次迭代除外)，ISTA的运行速度明显快于R-ISTA和IRLS，这是由于ISTA不需进行矩阵求逆运算，而IRLS和R-ISTA的每次迭代过程，都需计算伪逆矩阵B=LHL+μW，当待处理数据较复杂时，其计算量更大。本次计算环境为Intel Core i5，主频为2.3 GHz ，采用Windows平台下的Matlab实现。

表2 三种算法的运算时间对比

为减小R-ISTA计算量，本文在R-ISTA基础上引入主频约束，此时伪逆矩阵Bmain=LHL+μWmain只需求解一次，计算量显著减少，主频约束对运行速度的影响见表3。可见当只进行一次迭代时，主频约束对运行时间影响不大； 随着迭代次数的增加，对无主频约束的R-ISTA而言，伪逆矩阵要随之计算更新，导致其计算量显著增大； 而有主频约束的R-ISTA由于只需求解一次伪逆矩阵，之后不再随迭代次数增加而更新，且软阈值函数的相关计算量较小，当处理大量数据时，其计算量增加缓慢。

表3 有/无主频约束R-ISTA方法的迭代时间

3 结束语

本文将高分辨Radon变换中加权矩阵的思想引入ISTA方法，利用Radon参数的先验信息约束反演误差函数，提出R-ISTA方法，解决了传统软阈值算法用于Radon变换表现的分辨率低及收敛速度慢问题。模拟数据和实际资料处理结果表明，与ISTA和IRLS相比，所提R-ISTA的Radon变换的分辨率有所提升，且具有更强压制多次波能力。

由于R-ISTA方法对于每一个频率仍需计算加权矩阵并进行矩阵求逆运算，计算量较大，因此本文在压制多次波时，引入主频约束思想，提高了R-ISTA方法对大型数据的处理能力。