基于GA-SVM梯形区域的故障诊断与可靠配置
2021-08-17李默臣王福忠
姚 波,李默臣,王福忠
(1.沈阳师范大学 数学与系统科学学院,沈阳 110034;2.沈阳工程学院 基础教学部,沈阳 110136)
0 引 言
极点数据分类[1]是故障诊断技术应用的关键,如何采集少量样本并缩短分类器运行时间实现精准分类,一直是航空、航天飞控系统亟待解决的问题。支持向量机[2-4](support vector machine,SVM)作为一种基于统计学习理论且性能良好的学习机,在小样本学习上优势明显。但因SVM参量选取易受主观经验知识的影响,很大程度上限制了它的应用。因此如何提升其使用价值,设计容错性能好、能耗低的可靠控制器具有重要的理论意义。早期可靠控制[5-11]将系统可能发生的故障考虑在设计当中,一定程度上满足了系统的可靠性要求,但同时也存在保守性大、能耗高等问题。常用的网格搜寻法与“留一法”(leave-one-out)类似,都是需要根据人工经验确定一个最优参数集范围,进而在该参量集上遍历搜索最优组合值,一定程度上缩小了寻优范围,但计算量庞大[12]。文献[13]采用粒子群算法优化SVM参数,并以发动机4种尾气作为学习样本,实现故障信息的精准分类,但因惯性权值选取对分类结果影响较大,有时很难得到令人满意的模型。文献[14]采用实值编码遗传算法(genetic algorithms,GA)来实现SVM模型的参数选择,通过采集二值遥感图像建立模型得到了很好的训练效果。文献[15]结合遗传及粒子群算法的特点,形成一种混合算法,基于圆形区域下应用LSSVM实现故障诊断与可靠控制,仿真结果得到明显提升,但因组合算法具有程序复杂、变量较多的缺陷,很难立即得出想要结果。本文基于飞控系统提出采用实值GA算法实现SVM参数自动选择,通过构建训练模型并使极点稳定在梯形区域的方式保证系统达到期望的特性。对于未知飞控系统极点难以获取的问题,给出全维状态观测器的算法,实现了极点信息的实时观测。同时对比PSO-SVM、Gridsearch算法,分类准确率达到95.999 6%,说明了GA-SVM算法的全局性、高效性。得到的可靠控制器能有效识别系统故障,进一步证明该方法在主动容错和故障预警方面具有较高的推广价值。
1 SVM理论
支持向量机作为数理统计基础上发展起来的智能学习算法,设计之初主要用于解决数据分类、回归等问题。其核心思想是通过构建最优超平面使正例与反例之间的距离最大化。先假设存在一个样本集:

其中:yi=1为1类样本集;yi=-1为2类样本集。依据Largerange对偶原理,可得决策函数:

2 遗传算法(GA-SVM)模型建立
GA是一种模拟生物进化(交叉、变异等)而形成的智能学习算法。它在搜索空间不断捕获、累积数据空间信息,并通过控制搜索深度及广度的方式获取问题的最优解。针对SVM核参数g、惩罚因子c对诊断精度影响较大的问题,采用GA算法优化相关参数g和c,进而获得最佳诊断模型。具体流程如下:
步骤1 采集故障通道极点数据,形成极点信息库,并对所有源数据进行归一化处理,一半作为训练集构建粗糙模型,一半作为测试集用于模型评价;

步骤3 进行选择、交叉、变异等操作;
步骤4 判断是否终止循环的充要条件是输出最优组合参数,否则跳回步骤3继续运行;
步骤5 将最优的组合值g,c代入SVM中,形成最佳的GA-SVM模型,从而实现对故障通道的精准预测。
3 极点观测器的设计
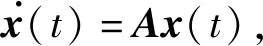
1=x(t1),2=x(t1+Δt),…,n=x(t1+nΔt)
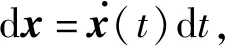

(1)
当Δt→0时,结果逐渐趋于真实值。令
Δxi=x(t1+iΔt)-x(t1+(i-1)Δt)
(2)
根据式(1)和式(2)可得

(3)
根据式(2)和式(3)可得
Δxi=Ax(t1+(i-1)Δt)Δt
而
ΔX=[Δx1,Δx2,…,Δxn-1],X=[x(t1),x(t2),…,x(tn)]Δt
若有X可逆,可得A的近似值为
A=ΔXX-1
(4)
4 GA-SVM算法在梯形区域的应用
给定如下线性定常系统:
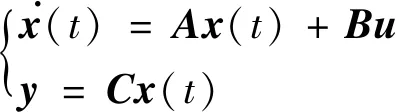
其中:x(t)∈n,y(t)∈p,u(t)∈m分别为系统的状态、输出及控制变量;A,B,C为满足维数要求的常数矩阵。若将静态输出控制器u(t)=Ky(t)引入,即有闭环系统:
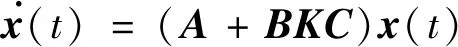
(5)
当执行器发生增益故障时,公式为uf(t)=Fau(t),此时闭环系统为

(6)

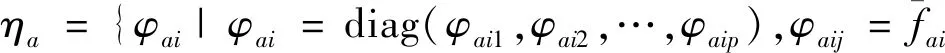

引理1 若M,A分别为正定对称矩阵、行满秩矩阵,则AMAT可逆。
证明 假设AMATX=0不存在非零解,结论成立。将X乘于方程的左侧,即XAMATX=0,整理(ATX)TM(ATX)=0,由于M为正定对称矩阵,则ATX=0,从而AATX=0,而AAT可逆,则只存在零解X=0,即AMAT可逆。
引理2[5]存在一个A矩阵,若保证极点均无法逃逸夹角为2θ的扇形区域,即存在正定矩阵X满足如下充要条件:
定理1[8]对于如上系统(5),假设加入静态反馈控制器,则保证极点均无法逃逸D(h1,h2)与D2θ组成的梯形区域的充要条件是存在一个正定矩阵X和矩阵U,满足下列条件:
其中(X,U)为可行解,相应的静态输出反馈控制器K=UW-1。且Φ=BUC+AX,W满足WC=CX条件。
定理2[8]对于如上系统(6),当发生执行器故障,保证极点均无法逃逸D(h1,h2)与D2θ组成的梯形区域的充要条件是存在一个正定矩阵X和矩阵U,满足下列条件:
其中(X,U)为可行解,相应的静态输出反馈控制器K=UW-1。其中Π=BαaiUC+AX,W满足WC=CX条件。
5 仿真研究
考虑如下机翼线性模型:
现假设系统极点稳定在h1=-15,h2=-1及θ=30°,θ=-30°形成的梯形区域Dd内,即等价于机翼满足相应的性能指标要求,否则该机翼出现执行器故障。给定静态反馈控制器为

此时极点均稳定在Dd内。
5.1 不同算法对比分析
现模拟机翼执行器增益故障,相应极点跳出梯形区域,系统的稳定性遭到破坏。极点分布情况如图1和图2所示。若对机翼故障F=diag(f1,f2)赋值如下,f2=1,0.6 图1 第1条通道故障极点分布Fig.1 Distribution of fault poles in the first channel 图2 针对第1条通道故障极点配置图Fig.2 Pole assignment chart for the first channel fault 现分别采用PSO及Gridsearch算法对SVM中的参数进行调整优化,当种群数量为30,学习率分别为c1=1.6,c2=1.5,最佳适应度曲线逐渐趋近93.333 3%,此时参数组合值为c=2.424,g=515.755。当c=1,g=512时得出的最佳精准率为92.555 6%,由此可判断这2种算法分类精度相差不大。为进一步提高分类精度,现采用GA-SVM算法,当LC=0.4,LM=0.01,种群数量为50,迭代次数为200时,极点分类准确率高达95.999 6%,通过以上3种算法对比不难发现,GA-SVM算法在梯形区域故障诊断模型中效果明显。 由于X可逆,即可根据公式(4)求出矩阵A。相应极点误差分别为0.07%,0.19%,0.16%,这直接证明了极点观测器是有效的。 现采用GA-SVM算法并结合极点观测器的特点对单通道执行器进行故障诊断,从而实现极点的可靠配置。图2所示极点均已稳定在梯形区域内,使机翼系统达到了理想状态。若非此方法,则需考虑执行器故障的所有先验知识,这会导致能量浪费。 文中基于极点观测器算法特点,解决了未知飞控系统极点信息难以采集的问题。同时,针对SVM选取参数易受主观先验知识影响的缺陷,提出一种依据系统输入输出参量自动寻优的GA-SVM算法。相较SVM算法,本算法具有运行时间短、收敛速度快、分类精度高等优点。从仿真结果可以看出,GA-SVM相比PSO-SVM、Gridsearch算法对于梯形区域下极点配置问题效果显著。所得到的控制器具有一定的鲁棒性,当执行器发生故障但极点仍处在梯形区域时,控制器不发挥作用;一旦极点跳出梯形区域,立即调换相应的可靠控制器,保持飞控系统稳定。该方法对于其他类型的SVM参量优化也具有一定的推广价值。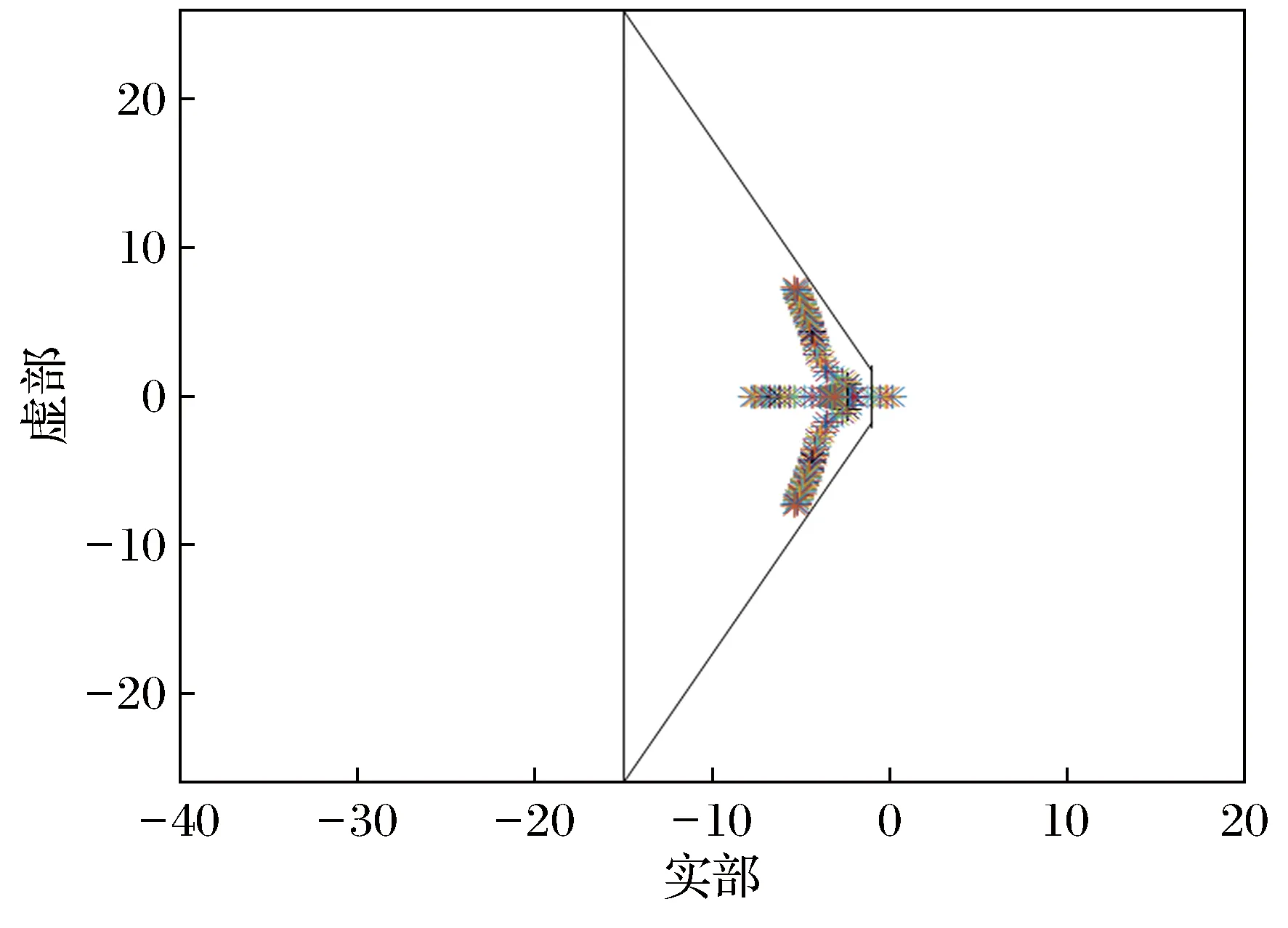

5.2 测试极点观测器及控制效果
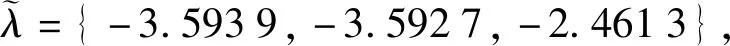
6 结 论
